第七章 7.2.1复数的加、减运算及其几何意义--人教A版高中数学必修第二册教学课件(共18张PPT)
文档属性
| 名称 | 第七章 7.2.1复数的加、减运算及其几何意义--人教A版高中数学必修第二册教学课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 537.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览






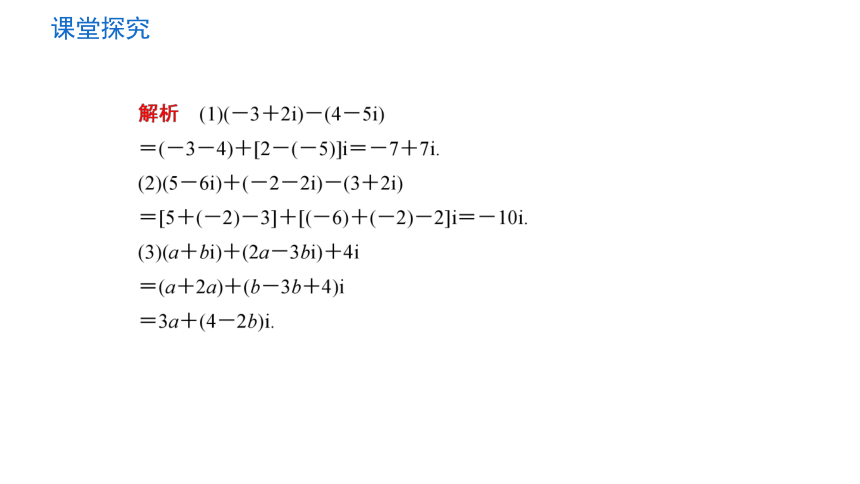
文档简介
(共18张PPT)
7.2.1 复数的加、减法运算及其几何意义
第七章 复数
数学
学习目标
①通过类比初中多项式加、减法的运算法则,掌握复数代数形式的加、减运算法则.
②通过向量加、减法的几何意义,了解复数代数形式的加、减运算的几何意义.
阅读课本75-76页,思考并完成以下问题
1.复数的加法、减法如何进行?复数加法、减法的几何意义如何?
2.复数的加、减法与向量间的加减运算是否相同?
自主预习
课堂导入
知识清单
课堂导入
课堂导入
题型分析
课堂探究
课堂探究
课堂探究
课堂探究
课堂探究
例2 根据复数及其运算的几何意义,求复平面内的两点Z1(x1,y1),Z2(x2,y2)间的距离.
解析 因为复平面内的点Z1(x1,y1),Z2(x2,y2)对应的复数分别为Z1=x1+y1i,Z2=x2+y2i,
所以Z1,Z2之间的距离为|Z1Z2|=||=|Z1-Z2|=|(x1-x2)+(y1-y2)|=.
向量加法、减法运算的平行四边形法则和三角形法则是复数加法、减法几何意义的依据.利用加法“首尾相接”和减法“指向被减数”的特点,在三角形内可求得第三个向量及其对应的复数.注意向量对应的复数是ZB-ZA(终点对应的复数减去起点对应的复数).
课堂探究
课堂探究
课堂探究
课堂探究
(1)|z-z0|表示复数z,z0的对应点之间的距离,在应用时,要把绝对值号内变为两复数差的形式.
(2)|z-z0|=r表示以z0对应的点为圆心,r为半径的圆.
(3)涉及复数模的最值问题以及点的轨迹问题,均可从两点间距离公式的复数表达形式入手进行分析判断,然后通过几何方法进行求解.
课堂探究
课堂探究
课堂小结
总结归纳
我们今天都讲了哪些知识?
谢谢大家
7.2.1 复数的加、减法运算及其几何意义
第七章 复数
数学
学习目标
①通过类比初中多项式加、减法的运算法则,掌握复数代数形式的加、减运算法则.
②通过向量加、减法的几何意义,了解复数代数形式的加、减运算的几何意义.
阅读课本75-76页,思考并完成以下问题
1.复数的加法、减法如何进行?复数加法、减法的几何意义如何?
2.复数的加、减法与向量间的加减运算是否相同?
自主预习
课堂导入
知识清单
课堂导入
课堂导入
题型分析
课堂探究
课堂探究
课堂探究
课堂探究
课堂探究
例2 根据复数及其运算的几何意义,求复平面内的两点Z1(x1,y1),Z2(x2,y2)间的距离.
解析 因为复平面内的点Z1(x1,y1),Z2(x2,y2)对应的复数分别为Z1=x1+y1i,Z2=x2+y2i,
所以Z1,Z2之间的距离为|Z1Z2|=||=|Z1-Z2|=|(x1-x2)+(y1-y2)|=.
向量加法、减法运算的平行四边形法则和三角形法则是复数加法、减法几何意义的依据.利用加法“首尾相接”和减法“指向被减数”的特点,在三角形内可求得第三个向量及其对应的复数.注意向量对应的复数是ZB-ZA(终点对应的复数减去起点对应的复数).
课堂探究
课堂探究
课堂探究
课堂探究
(1)|z-z0|表示复数z,z0的对应点之间的距离,在应用时,要把绝对值号内变为两复数差的形式.
(2)|z-z0|=r表示以z0对应的点为圆心,r为半径的圆.
(3)涉及复数模的最值问题以及点的轨迹问题,均可从两点间距离公式的复数表达形式入手进行分析判断,然后通过几何方法进行求解.
课堂探究
课堂探究
课堂小结
总结归纳
我们今天都讲了哪些知识?
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
