第八章 8.6.1直线与直线垂直--人教A版高中数学必修第二册教学课件(共40张PPT)
文档属性
| 名称 | 第八章 8.6.1直线与直线垂直--人教A版高中数学必修第二册教学课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:52:32 | ||
图片预览





文档简介
(共19张PPT)
8.6.1直线与直线垂直
第八章 立体几何初步
数学
一、学习目标
(1)理解异面直线夹角的定义,会求异面直线所成角;
(2)理解两条直线垂直的定义,并能够根据所给条件证明两条直线互相垂直.
【导入新课】
二、课堂探究
【问题探究1】如图所示,在正方体ABCD-A'B'C'D'中,直线A'C'与直线AB,直线A'D'与直线AB都是异面直线,直线A'C'与直线A'D'相对于直线AB的位置相同么?如果不同,如何表示这种差异呢
结论:我们知道,平面内两条直线相交形成4个角,其中不大于90°的角称为这两条直线所成的角(或夹角),它刻画了一条直线相对于另一条直线倾斜的程度;类似地,我们也可以用“异面直线所成的角”来刻画两条异面直线的位置关系.
二、课堂探究
思考1:那么如何定义异面直线所成的角呢?阅读教材,并将下面空白位置补充完整.
如图,已知两条异面直线a,b,经过空间任一点O分别作________,________,我们把________________叫做异面直线a与b所成的角(或夹角).
如果两条异面直线所成的角是直角,那么我们就说这两条异面直线___________. 直线 a 与直线 b 垂直,记作______.
当两条直线a,b相互平行时,我们规定它们所成的角为_____. 所以空间两条直线所成角的取值范围是____________.
直线 a'与b'
互相垂直
a⊥b
0°
0°≤ α ≤90°
二、课堂探究
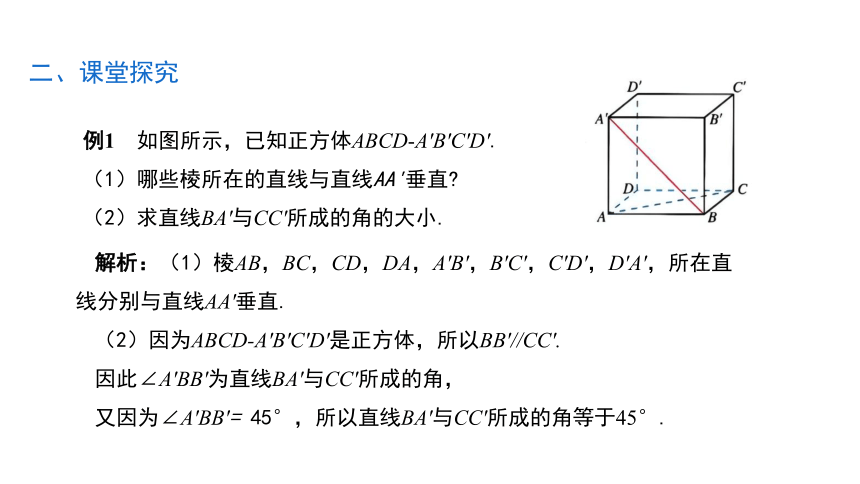
例1 如图所示,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线AA'垂直
(2)求直线BA'与CC'所成的角的大小.
解析:(1)棱AB,BC,CD,DA,A'B',B'C',C'D',D'A',所在直线分别与直线AA'垂直.
(2)因为ABCD-A'B'C'D'是正方体,所以BB'//CC'.
因此∠A'BB'为直线BA'与CC'所成的角,
又因为∠A'BB'= 45°,所以直线BA'与CC'所成的角等于45°.
二、课堂探究
【小试牛刀】
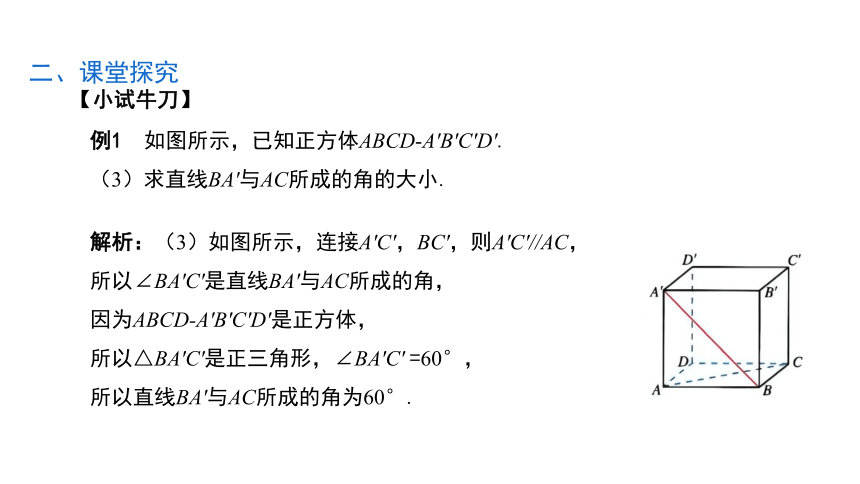
例1 如图所示,已知正方体ABCD-A'B'C'D'.
(3)求直线BA'与AC所成的角的大小.
解析:(3)如图所示,连接A'C',BC',则A'C'//AC,
所以∠BA'C'是直线BA'与AC所成的角,
因为ABCD-A'B'C'D'是正方体,
所以△BA'C'是正三角形,∠BA'C' =60°,
所以直线BA'与AC所成的角为60°.
二、课堂探究
【跟踪训练】
如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是________;
(2)AC和D1C1所成的角是________;
(3)AC和B1D1所成的角是________;
(4)AC和A1B所成的角是________.
(1)90°.
(2)45°.
(3)90°.
(4)60°.
二、课堂探究
【小试牛刀】
例2 如图(1)所示,在正方体ABCD-A1B1C1D1中,O1为底面A1B1C1D1的中心.求证:AO1⊥BD.
证明:如图(2),连接B1D1,AB1,AD1,
在正方体ABCD-A1B1C1D1中,易知B1D1//BD,
所以AO1与B1D1所成的角即为AO1与BD所成的角,
在△AB1D1中,因为AB1=AD1,O1为B1D1中点,
所以AO1⊥B1D1,又B1D1//BD,
所以AO1⊥BD.
二、课堂探究
【跟踪训练】
如图所示,在空间四边形ABCD中,AD =BC = 2,E,F分别是AB,CD的中点,EF= .
求证:AD⊥BC.
二、课堂探究
【跟踪训练】
证明:如图所示,取BD 的中点H,连接EH,FH.
因为E是AB的中点,且AD =2,
所以EH∥AD,EH =1.同理FH∥BC,FH =1.
所以∠EHF(或其补角)是异面直线AD,BC所成的角.
因为EF= ,所以EH 2+FH 2=EF 2,
所以△EFH是等腰直角三角形,EF是斜边,
所以∠EHF=90°,即AD与BC所成的角是90°,
所以AD⊥BC.
二、课堂探究
【名师解惑】
证明两条异面直线垂直的关键是证明两条异面直线所成角为90°.
二、课堂探究
1. 如图,三棱柱ABC A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是( ).
A.直线CC1与直线B1E相交 B.CC1与AE共面
C.AE与B1C1是异面直线 D.AE与B1C1垂直
ACD
三、课堂练习
三、课堂练习
C
2.如图所示,在正方体ABCD-A1B1C1D1中,①DA1与BC1平行;②DD1与BC1垂直;③A1B1与BC1垂直.以上三个结论中,正确结论的序号是( )
A.①② B.②③
C.③ D.①②③
三、课堂练习
3.如图所示,正方体AC1中,E,F分别是A1B1,B1C1的中点,求证:DB1⊥EF.
证明 如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
可知∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
∴DB1⊥EF.
4.如图所示,正方体AC1中,E、F分别是A1B1、B1C1的中点,
求证:DB1⊥EF.
证明:如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
∴DB1⊥EF.
三、课堂练习
四、课堂小结
(1)异面直线所成角的定义、范围及求法;
(2)异面直线相互垂直的定义,及直线与直线相互垂直的证明方法.
五、课后作业
必做题:完成学案后的课后巩固.
选做题:完成学案后的核心素养专练
谢谢大家
8.6.1直线与直线垂直
第八章 立体几何初步
数学
一、学习目标
(1)理解异面直线夹角的定义,会求异面直线所成角;
(2)理解两条直线垂直的定义,并能够根据所给条件证明两条直线互相垂直.
【导入新课】
二、课堂探究
【问题探究1】如图所示,在正方体ABCD-A'B'C'D'中,直线A'C'与直线AB,直线A'D'与直线AB都是异面直线,直线A'C'与直线A'D'相对于直线AB的位置相同么?如果不同,如何表示这种差异呢
结论:我们知道,平面内两条直线相交形成4个角,其中不大于90°的角称为这两条直线所成的角(或夹角),它刻画了一条直线相对于另一条直线倾斜的程度;类似地,我们也可以用“异面直线所成的角”来刻画两条异面直线的位置关系.
二、课堂探究
思考1:那么如何定义异面直线所成的角呢?阅读教材,并将下面空白位置补充完整.
如图,已知两条异面直线a,b,经过空间任一点O分别作________,________,我们把________________叫做异面直线a与b所成的角(或夹角).
如果两条异面直线所成的角是直角,那么我们就说这两条异面直线___________. 直线 a 与直线 b 垂直,记作______.
当两条直线a,b相互平行时,我们规定它们所成的角为_____. 所以空间两条直线所成角的取值范围是____________.
直线 a'与b'
互相垂直
a⊥b
0°
0°≤ α ≤90°
二、课堂探究
例1 如图所示,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线AA'垂直
(2)求直线BA'与CC'所成的角的大小.
解析:(1)棱AB,BC,CD,DA,A'B',B'C',C'D',D'A',所在直线分别与直线AA'垂直.
(2)因为ABCD-A'B'C'D'是正方体,所以BB'//CC'.
因此∠A'BB'为直线BA'与CC'所成的角,
又因为∠A'BB'= 45°,所以直线BA'与CC'所成的角等于45°.
二、课堂探究
【小试牛刀】
例1 如图所示,已知正方体ABCD-A'B'C'D'.
(3)求直线BA'与AC所成的角的大小.
解析:(3)如图所示,连接A'C',BC',则A'C'//AC,
所以∠BA'C'是直线BA'与AC所成的角,
因为ABCD-A'B'C'D'是正方体,
所以△BA'C'是正三角形,∠BA'C' =60°,
所以直线BA'与AC所成的角为60°.
二、课堂探究
【跟踪训练】
如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是________;
(2)AC和D1C1所成的角是________;
(3)AC和B1D1所成的角是________;
(4)AC和A1B所成的角是________.
(1)90°.
(2)45°.
(3)90°.
(4)60°.
二、课堂探究
【小试牛刀】
例2 如图(1)所示,在正方体ABCD-A1B1C1D1中,O1为底面A1B1C1D1的中心.求证:AO1⊥BD.
证明:如图(2),连接B1D1,AB1,AD1,
在正方体ABCD-A1B1C1D1中,易知B1D1//BD,
所以AO1与B1D1所成的角即为AO1与BD所成的角,
在△AB1D1中,因为AB1=AD1,O1为B1D1中点,
所以AO1⊥B1D1,又B1D1//BD,
所以AO1⊥BD.
二、课堂探究
【跟踪训练】
如图所示,在空间四边形ABCD中,AD =BC = 2,E,F分别是AB,CD的中点,EF= .
求证:AD⊥BC.
二、课堂探究
【跟踪训练】
证明:如图所示,取BD 的中点H,连接EH,FH.
因为E是AB的中点,且AD =2,
所以EH∥AD,EH =1.同理FH∥BC,FH =1.
所以∠EHF(或其补角)是异面直线AD,BC所成的角.
因为EF= ,所以EH 2+FH 2=EF 2,
所以△EFH是等腰直角三角形,EF是斜边,
所以∠EHF=90°,即AD与BC所成的角是90°,
所以AD⊥BC.
二、课堂探究
【名师解惑】
证明两条异面直线垂直的关键是证明两条异面直线所成角为90°.
二、课堂探究
1. 如图,三棱柱ABC A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是( ).
A.直线CC1与直线B1E相交 B.CC1与AE共面
C.AE与B1C1是异面直线 D.AE与B1C1垂直
ACD
三、课堂练习
三、课堂练习
C
2.如图所示,在正方体ABCD-A1B1C1D1中,①DA1与BC1平行;②DD1与BC1垂直;③A1B1与BC1垂直.以上三个结论中,正确结论的序号是( )
A.①② B.②③
C.③ D.①②③
三、课堂练习
3.如图所示,正方体AC1中,E,F分别是A1B1,B1C1的中点,求证:DB1⊥EF.
证明 如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
可知∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
∴DB1⊥EF.
4.如图所示,正方体AC1中,E、F分别是A1B1、B1C1的中点,
求证:DB1⊥EF.
证明:如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G.
则OG∥B1D,EF∥A1C1.
∴∠GOA1为异面直线DB1与EF所成的角或其补角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
∴DB1⊥EF.
三、课堂练习
四、课堂小结
(1)异面直线所成角的定义、范围及求法;
(2)异面直线相互垂直的定义,及直线与直线相互垂直的证明方法.
五、课后作业
必做题:完成学案后的课后巩固.
选做题:完成学案后的核心素养专练
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
