11.2一元一次不等式 课件(共20张PPT) 人教版七年级数学下册
文档属性
| 名称 | 11.2一元一次不等式 课件(共20张PPT) 人教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第11单元 · 不等式与不等式组
11.2 一元一次不等式
1、等号两边都是整式,且都只含有____个未知数,未知数的次数都是_____,这样的方程叫做一元一次方程.
复习旧知
2、解一元一次方程:
(1) 5X+15=4X-1 (2)2(X+5)=3(X-5)
解:移项得:5x- 4x=-1 – 15
合并同类项,得:x= -26
解:去括号,得:2x+10 = 3x-15
移项,得:2x- 3x= -15 – 10
合并同类项,得:-1x= -25
系数化为1,得:x=25
1、下面的不等式:x-7>26,3x<2x+1,x>50,
-4x>3 都是只含有____个未知数,并且未知数的
次数是_____.
2、含有 个未知数,未知数的 的
不等式,叫做一元一次不等式.
3、下列不等式中,哪些是一元一次不等式?
①3+5>7;②x+y≤9;③ ;④-2x>5.
答:__________
知 识 点 一
一元一次不等式的定义
1
1
1
次数是1
④
讲授新课
例1 解下列不等式,并在数轴上表示解集:
(1)2(1+x)<3
解: 去括号,得: .
移项,得: .
合并同类项,得: .
系数化为1,得: .
这个不等式的解集在数轴上的表示:
知 识 点 二
一元一次不等式的解法
2+2x<3
2x<3-2
2x<1
X<
0
讲授新课
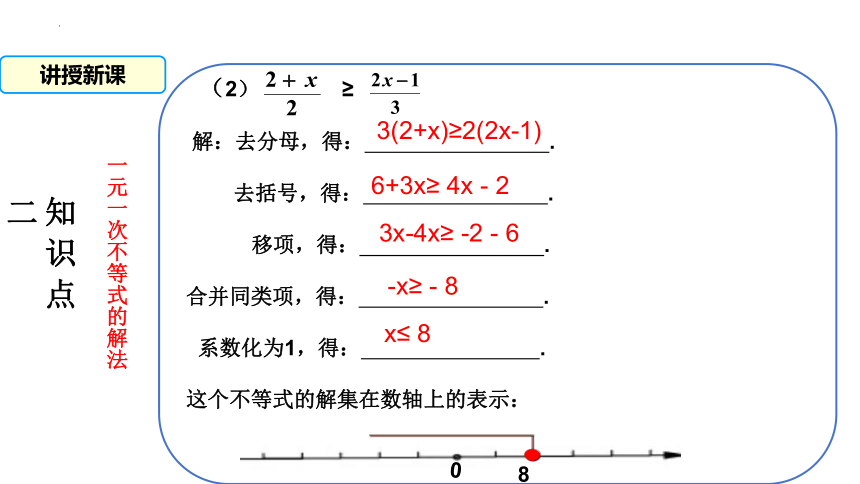
(2) ≥
解:去分母,得: .
去括号,得: .
移项,得: .
合并同类项,得: .
系数化为1,得: .
这个不等式的解集在数轴上的表示:
知 识 点 二
一元一次不等式的解法
6+3x≥ 4x - 2
3x-4x≥ -2 - 6
-x≥ - 8
x≤ 8
0
8
3(2+x)≥2(2x-1)
讲授新课
知 识 点 三
一元一次不等式的解法及练习
负数
改变
X=a
xX>a
注意:当不等式的两边都乘或除以同一个 时,
不等号的方向 .归纳:解一元一次方程,要根
据等式的性质,将方程逐步化为 的形式;
而解一元一次不等式,则要根据不等式的性质,将不等
式逐步化为 (或 )的形式.
讲授新课
通过类比,探究解法
一般地,利用不等式的性质,采取与解一元一次方程类似的步骤,就可以求出一元一次不等式的解集。
解一元一次方程的依据和一般步骤,对你解一元一次不等式有什么启发?
解一元一次不等式的步骤:
注意:未知数的系数为正数,不等号方向不变;若是负数,则方向要改变
解:设这个市今年万元地区生产总值耗能为 t标准煤.
今年万元地区生产总值耗能比去年下降 t标准煤,
根据题意,列得不等式 ≥ ,
去分母,得 0.320-x≥ ,
移项,合并同类项,得 -x≥ .
系数化为1,得x ≤ .
答:这个市今年万元地区生产总值耗能至多为 t标准煤.
x
(0.320-x)
5%
0.320×5%
-0.304
0.304
0.304
探究新知
1.七年级举办古诗词知识竞赛,共有20道题,每一题答对得10分,答错或不答都扣5分.如果规定初赛成绩超过90分晋级决赛,那么至少要答对多少道题才能成功晋级?
解:设初赛答对了x道题.
根据题意,得10x-5(20-x)>90.
解这个不等式,得x>12.
答:初赛至少要答对13道题才能成功晋级.
巩固练习
由x应为正整数,可得x至少为13.
2.某工程队计划在10天内修路6km.施工前2天修完1.2km后,计划发生变化,准备至少提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天要修路xkm.
根据题意,得(10-2-2)x≥6-1.2.
解这个不等式,得x≥0.8.
答:以后几天内平均每天至少要修路0.8km.
巩固练习
1.解下列不等式,并在数轴上表示解集.
随堂练习
解:去分母,得:6-3(x+1)>2(4-x)
去括号,得:6-3x-3>8-2x
移项,得:-3x+2x>8-6+3
合并同类项,得:-x>5
系数化为1,得:x<-5
这个不等式的解集在数轴上表示如图所示
-5
0
解:去分母,得:3(x-1)<7(2x+5)
去括号,得:3x-3<14x+35
移项,得: 3x-14x<35+3
合并同类项,得:-11x<38
系数化为1,得: x>
这个不等式的解集在数轴上表示如图所示
0
2. 求不等式 ≥0的负整数解.
解:去分母,得:2(3x-1)-5(x-1)≥0
去括号,得: 6x-2-5x+5≥0
移项、得: 6x-5x≥2-5
合并同类项、得 x≥-3
所以原不等式的负整数解为x=-3,-2,-1.
4.怎样解不等式 >70%
5.比较解(4)中的不等式与解方程
的步骤,两者有什么不同吗
3.与x有关的哪个式子的值应超过70% 这个式
子表示什么
例:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少
解:(1)当累计购物不超过50元时,在甲、乙两商
场购物都不享受优惠,且两商场以同样价格出
售同样的商品,因此到两商场购物花费一样.
解:(2)当累计购物超过50元而不超过100元时,享
受乙商场的购物优惠,不享受甲商场的购物优
惠,因此到乙商场购物花费少.
(2) 2(x+5) ≤ 3(x-5) ;
解:去括号,得 2x+10≤3x-15.
移项, 得 2x-3x ≤ -15-10 .
合并同类项,得 -x ≤ -25.
系数化为1, 得 x ≥ 25.
这个不等式的解集在数轴上的表示如图所示.
巩固练习
25
0
解:去分母,得 3(x-1)>7(2x+5).
去括号,得 3x-3 > 14x+35.
移项, 得 3x-14x > 35+3.
合并同类项,得 -11x > 38.
系数化为1,得 x < .
这个不等式的解集在数轴上的表示如图所示.
巩固练习
0
(3) ;
>
解:去分母,得 2(x+1) ≥ 3(2x-5)+12.
去括号,得 2x+2 ≥ 6x-15+12.
移项,得 2x-6x ≥ -15+12-2.
合并同类项,得 -4x≥ -5.
系数化为1,得 x ≤ .
这个不等式的解集在数轴上的表示如图所示.
巩固练习
0
(4) .
≥
第11单元 · 不等式与不等式组
11.2 一元一次不等式
1、等号两边都是整式,且都只含有____个未知数,未知数的次数都是_____,这样的方程叫做一元一次方程.
复习旧知
2、解一元一次方程:
(1) 5X+15=4X-1 (2)2(X+5)=3(X-5)
解:移项得:5x- 4x=-1 – 15
合并同类项,得:x= -26
解:去括号,得:2x+10 = 3x-15
移项,得:2x- 3x= -15 – 10
合并同类项,得:-1x= -25
系数化为1,得:x=25
1、下面的不等式:x-7>26,3x<2x+1,x>50,
-4x>3 都是只含有____个未知数,并且未知数的
次数是_____.
2、含有 个未知数,未知数的 的
不等式,叫做一元一次不等式.
3、下列不等式中,哪些是一元一次不等式?
①3+5>7;②x+y≤9;③ ;④-2x>5.
答:__________
知 识 点 一
一元一次不等式的定义
1
1
1
次数是1
④
讲授新课
例1 解下列不等式,并在数轴上表示解集:
(1)2(1+x)<3
解: 去括号,得: .
移项,得: .
合并同类项,得: .
系数化为1,得: .
这个不等式的解集在数轴上的表示:
知 识 点 二
一元一次不等式的解法
2+2x<3
2x<3-2
2x<1
X<
0
讲授新课
(2) ≥
解:去分母,得: .
去括号,得: .
移项,得: .
合并同类项,得: .
系数化为1,得: .
这个不等式的解集在数轴上的表示:
知 识 点 二
一元一次不等式的解法
6+3x≥ 4x - 2
3x-4x≥ -2 - 6
-x≥ - 8
x≤ 8
0
8
3(2+x)≥2(2x-1)
讲授新课
知 识 点 三
一元一次不等式的解法及练习
负数
改变
X=a
x
注意:当不等式的两边都乘或除以同一个 时,
不等号的方向 .归纳:解一元一次方程,要根
据等式的性质,将方程逐步化为 的形式;
而解一元一次不等式,则要根据不等式的性质,将不等
式逐步化为 (或 )的形式.
讲授新课
通过类比,探究解法
一般地,利用不等式的性质,采取与解一元一次方程类似的步骤,就可以求出一元一次不等式的解集。
解一元一次方程的依据和一般步骤,对你解一元一次不等式有什么启发?
解一元一次不等式的步骤:
注意:未知数的系数为正数,不等号方向不变;若是负数,则方向要改变
解:设这个市今年万元地区生产总值耗能为 t标准煤.
今年万元地区生产总值耗能比去年下降 t标准煤,
根据题意,列得不等式 ≥ ,
去分母,得 0.320-x≥ ,
移项,合并同类项,得 -x≥ .
系数化为1,得x ≤ .
答:这个市今年万元地区生产总值耗能至多为 t标准煤.
x
(0.320-x)
5%
0.320×5%
-0.304
0.304
0.304
探究新知
1.七年级举办古诗词知识竞赛,共有20道题,每一题答对得10分,答错或不答都扣5分.如果规定初赛成绩超过90分晋级决赛,那么至少要答对多少道题才能成功晋级?
解:设初赛答对了x道题.
根据题意,得10x-5(20-x)>90.
解这个不等式,得x>12.
答:初赛至少要答对13道题才能成功晋级.
巩固练习
由x应为正整数,可得x至少为13.
2.某工程队计划在10天内修路6km.施工前2天修完1.2km后,计划发生变化,准备至少提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天要修路xkm.
根据题意,得(10-2-2)x≥6-1.2.
解这个不等式,得x≥0.8.
答:以后几天内平均每天至少要修路0.8km.
巩固练习
1.解下列不等式,并在数轴上表示解集.
随堂练习
解:去分母,得:6-3(x+1)>2(4-x)
去括号,得:6-3x-3>8-2x
移项,得:-3x+2x>8-6+3
合并同类项,得:-x>5
系数化为1,得:x<-5
这个不等式的解集在数轴上表示如图所示
-5
0
解:去分母,得:3(x-1)<7(2x+5)
去括号,得:3x-3<14x+35
移项,得: 3x-14x<35+3
合并同类项,得:-11x<38
系数化为1,得: x>
这个不等式的解集在数轴上表示如图所示
0
2. 求不等式 ≥0的负整数解.
解:去分母,得:2(3x-1)-5(x-1)≥0
去括号,得: 6x-2-5x+5≥0
移项、得: 6x-5x≥2-5
合并同类项、得 x≥-3
所以原不等式的负整数解为x=-3,-2,-1.
4.怎样解不等式 >70%
5.比较解(4)中的不等式与解方程
的步骤,两者有什么不同吗
3.与x有关的哪个式子的值应超过70% 这个式
子表示什么
例:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少
解:(1)当累计购物不超过50元时,在甲、乙两商
场购物都不享受优惠,且两商场以同样价格出
售同样的商品,因此到两商场购物花费一样.
解:(2)当累计购物超过50元而不超过100元时,享
受乙商场的购物优惠,不享受甲商场的购物优
惠,因此到乙商场购物花费少.
(2) 2(x+5) ≤ 3(x-5) ;
解:去括号,得 2x+10≤3x-15.
移项, 得 2x-3x ≤ -15-10 .
合并同类项,得 -x ≤ -25.
系数化为1, 得 x ≥ 25.
这个不等式的解集在数轴上的表示如图所示.
巩固练习
25
0
解:去分母,得 3(x-1)>7(2x+5).
去括号,得 3x-3 > 14x+35.
移项, 得 3x-14x > 35+3.
合并同类项,得 -11x > 38.
系数化为1,得 x < .
这个不等式的解集在数轴上的表示如图所示.
巩固练习
0
(3) ;
>
解:去分母,得 2(x+1) ≥ 3(2x-5)+12.
去括号,得 2x+2 ≥ 6x-15+12.
移项,得 2x-6x ≥ -15+12-2.
合并同类项,得 -4x≥ -5.
系数化为1,得 x ≤ .
这个不等式的解集在数轴上的表示如图所示.
巩固练习
0
(4) .
≥
同课章节目录
