八年级数学人教版下册期末达标测试卷(含答案)
文档属性
| 名称 | 八年级数学人教版下册期末达标测试卷(含答案) | 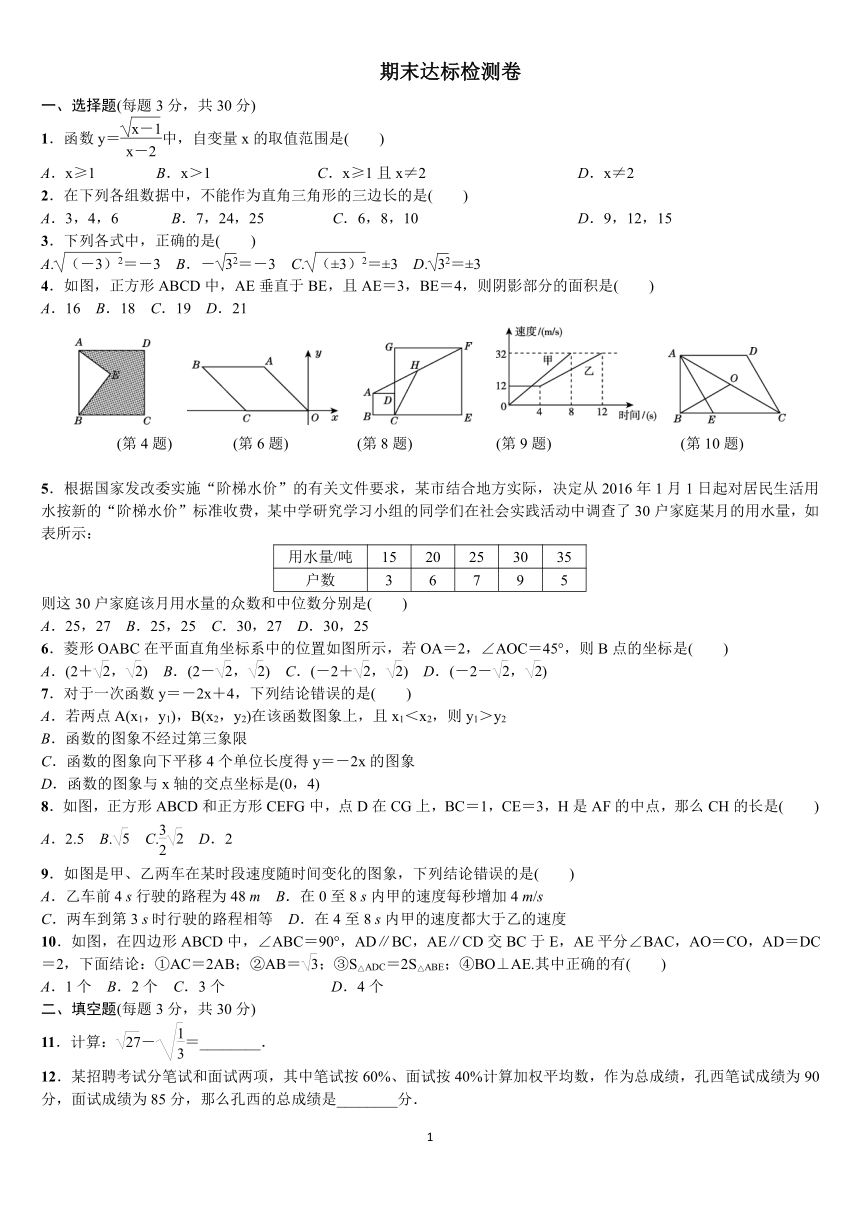 | |
| 格式 | doc | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 14:07:28 | ||
图片预览




文档简介
期末达标检测卷
一、选择题(每题3分,共30分)
1.函数y=中,自变量x的取值范围是( )
A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠2
2.在下列各组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
3.下列各式中,正确的是( )
A.=-3 B.-=-3 C.=±3 D.=±3
4.如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
INCLUDEPICTURE"sa42.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa42.tif" \* MERGEFORMATINET
(第4题) (第6题) (第8题) (第9题) (第10题)
5.根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
用水量/吨 15 20 25 30 35
户数 3 6 7 9 5
则这30户家庭该月用水量的众数和中位数分别是( )
A.25,27 B.25,25 C.30,27 D.30,25
6.菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=45°,则B点的坐标是( )
A.(2+,) B.(2-,) C.(-2+,) D.(-2-,)
7.对于一次函数y=-2x+4,下列结论错误的是( )
A.若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1>y2
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得y=-2x的图象
D.函数的图象与x轴的交点坐标是(0,4)
8.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A.2.5 B. C. D.2
9.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙车前4 s行驶的路程为48 m B.在0至8 s内甲的速度每秒增加4 m/s
C.两车到第3 s时行驶的路程相等 D.在4至8 s内甲的速度都大于乙的速度
10.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共30分)
11.计算:-=________.
12.某招聘考试分笔试和面试两项,其中笔试按60%、面试按40%计算加权平均数,作为总成绩,孔西笔试成绩为90分,面试成绩为85分,那么孔西的总成绩是________分.
13.一次函数y=(3-a)x+b-2在直角坐标系中的图象如图所示,化简|b-a|--|2-b|=________.
INCLUDEPICTURE"tu23.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\tu23.tif" \* MERGEFORMATINET
(第13题) (第15题) (第16题) (第17题)
14.某超市利用五一开展促销活动,店前公告如下:一次性购买某种服装3件,每件仅售80元,如果超过3件,则超过部分打八折,顾客所付款y(元)与所购服装件数x(x≥3)之间的函数关系式为______________.
15.将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中(如图),设筷子露在杯子外面的长度为h cm,则h的取值范围是______________.
16.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,连接EF.若AB=10,则EF的长是________.
17.如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=45°,则=________.
18.如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b<x的解集为__________.
INCLUDEPICTURE"sa48.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa48.tif" \* MERGEFORMATINET
(第18题) (第19题) (第20题)
19.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的区域面积为________.
20.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为__________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.(1)计算:2+3--;
(2)已知x=2+,y=2-,求代数式·的值.
22.如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
INCLUDEPICTURE"sa51.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa51.tif" \* MERGEFORMATINET
23.已知a,b,c满足|a-|++(c-4)2=0.
(1)求a,b,c的值.
(2)判断以a,b,c为边能否构成三角形?若能构成三角形,此三角形是什么形状,并求出三角形的面积;若不能,请说明理由.
24.某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形统计图;
(2)写出这20名学生每人植树量的众数和中位数;
(2)估计这240名学生共植树多少棵.
25.如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为4的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
INCLUDEPICTURE"XT20.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\XT20.tif" \* MERGEFORMATINET
26.新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4 000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
(方案一)降价8%,另外每套房赠送a元装修基金;
(方案二)降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数解析式;
(2)老王要购买第十六层的一套房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
答案
一、1.C 2.A 3.B 4.C 5.D 6.D
7.D 点拨:k=-2<0,∴y随x的增大而减小,故A正确;k<0,b>0,图象过第一、二、四象限,B正确;函数图象向下平移4个单位长度得y=-2x的图象,C正确;函数的图象与x轴的交点坐标是(2,0),D错误.
8.B 点拨:如图,
INCLUDEPICTURE"adj115.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\adj115.tif" \* MERGEFORMATINET (第8题)
连接AC,CF,
在正方形ABCD和正方形CEFG中,
∵BC=1,CE=3,
∴AC=,CF=3.
∵∠ACD=∠GCF=45°,
∴∠ACF=45°+45°=90°.
∴△ACF是直角三角形.
由勾股定理得,AF==2.
∵H是AF的中点,∴CH=AF=.
故选B.
9.C
10.D 点拨:连接ED,如图所示.∵AD∥BC,DC∥AE,∴四边形AECD是平行四边形.又∵AD=DC,∴四边形AECD是菱形.又∵AO=CO,∴ED过点O且AC⊥ED,∠EAO=∠DAO.∵AE平分∠BAO,∴∠BAE=∠OAE.又∵∠ABE=∠AOE=90°,AE=AE,∴△BAE≌△OAE(AAS),∴AB=AO,EB=EO.∴AC=2AO=2AB.∵∠BAE=∠OAE,∠EAO=∠DAO,且易知∠BAD=90°,∴∠BAE=∠EAO=∠OAD=30°.∵四边形AECD是菱形,AD=2,∴AE=2,∴BE=1,∴AB=,且S△ADC=×AD×AB=×2BE×AB=2×BE×AB=2S△ABE.∵AB=AO,EB=EO,∴AE垂直平分BO,∴①②③④均正确.
INCLUDEPICTURE"sa54.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa54.tif" \* MERGEFORMATINET (第10题)
二、11. 12.88 13.1
14.y=64x+48(x≥3)
15.11≤h≤12
16.5 点拨:连接CD,易证四边形EFCD为平行四边形,则EF=CD,再利用直角三角形斜边上的中线等于斜边的一半即可求解.
17. 18.3<x<6
19.16 点拨:如图.
INCLUDEPICTURE"adj116a.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\adj116a.tif" \* MERGEFORMATINET (第19题)
∵点A、B的坐标分别为(1,0)、(4,0),∴AB=3.
∵∠CAB=90°,BC=5,
∴由勾股定理可得AC=4,∴A′C′=4.
∵点C′在直线y=2x-6上,
∴2x-6=4,解得x=5.
即OA′=5.∴CC′=5-1=4,
∴S BCC′B′=4×4=16,
即线段BC扫过的区域面积为16.
故答案为16.
20.(2.5,4)或(3,4)或(2,4)或(8,4) 点拨:∵四边形OABC是矩形,点A坐标为(10,0),点C坐标为(0,4),
∴∠OCB=90°,OC=4,BC=OA=10.∵D为OA的中点,∴OD=AD=5.①当PO=PD时,如图①,点P在OD的垂直平分线上,∴点P的坐标为(2.5,4);②当OP=OD时,如图②所示,则OP=OD=5,PC==3,∴点P的坐标为(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3.分两种情况:当E在D的左侧时,如图③所示,OE=5-3=2,∴点P的坐标为(2,4);当E在D的右侧时,如图④所示,OE=5+3=8,∴点P的坐标为(8,4).综上所述:点P的坐标为(2.5,4)或(3,4)或(2,4)或(8,4).
INCLUDEPICTURE"sa55.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa55.tif" \* MERGEFORMATINET (第20题)
三、21.解:(1)原式=4+3×--×4=4+2-4=2.
(2)原式=·=·=-.
当x=2+,y=2-时,
原式=-=-4.
22.解:(1)把(-2,-1),(1,3)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=x+.
(2)把x=0代入y=x+得y=,
∴D点的坐标为,
∴S△AOB=S△AOD+S△BOD=××2+××1=.
23.解:(1)∵a,b,c满足|a-|++(c-4)2=0,
∴|a-|=0,=0,(c-4)2=0,解得a=,b=5,c=4.
(2)∵a=,b=5,c=4,
∴a+b=+5>4,
∴以a,b,c为边能构成三角形.
∵a2+b2=()2+52=32=(4)2=c2,
∴此三角形是直角三角形.
∴S=××5=.
24.解:(1)D类的人数为:20-4-8-6=2.补全条形统计图略.
(2)由图可知,植树5棵的人数最多,所以,众数为5.按照植树的棵数从少到多排列,第10人与第11人都是植5棵树,所以,中位数是5.
(3)x==5.3(棵),240×5.3=1 272(棵).
答:估计这240名学生共植树1 272棵.
25.(1)证明:∵CE∥AD且CE=AD,
∴四边形ADCE是平行四边形.
∵在△ABC中,AB=AC,AD平分∠BAC,∴AD⊥BC(等腰三角形三线合一),∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)解:∵△ABC是等边三角形,边长为4,AD平分∠BAC,∴AC=BC=4=2CD,∠DAC=30°.∴CD=2.又∵CE∥AD,∴∠ACE=∠DAC=30°.∵四边形ADCE是矩形,∴AE=CD=2,OC=OA=AC=2,∠AEC=90°,∴CE===2.
∵FC=CO,∴FC=2.
如图,过O作OH⊥CE于H,
∵∠ACE=30°,∴OH=OC=1,
∴S四边形AOFE=S△AEC-S△COF=×2×2-×2×1=2-1.
INCLUDEPICTURE"XT22.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\XT22.tif" \* MERGEFORMATINET (第25题)
26.解:(1)当1≤x≤8时,y=4 000-30(8-x)=4 000-240+30x=30x+3 760;
当9≤x≤23时,y=4 000+50(x-8)=4 000+50x-400=50x+3 600.
∴所求函数解析式为
y=
(2)当x=16时,
方案一每套房总费用为w1=120×(50×16+3 600)×(1-8%)-a=485 760-a(元).
方案二每套房总费用为w2=120×(50×16+3 600)×(1-10%)=475 200(元).
∴当w1<w2,即485 760-a<475 200时,a>10 560;
当w1=w2,即485 760-a=475 200时,a=10 560;
当w1>w2,即485 760-a>475 200时,a<10 560.
因此当每套房赠送装修基金多于10 560元时,选择方案一合算;
当每套房赠送装修基金等于10 560元时,两种方案一样;
当每套房赠送装修基金少于10 560元时,选择方案二合算.
一、选择题(每题3分,共30分)
1.函数y=中,自变量x的取值范围是( )
A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠2
2.在下列各组数据中,不能作为直角三角形的三边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
3.下列各式中,正确的是( )
A.=-3 B.-=-3 C.=±3 D.=±3
4.如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
INCLUDEPICTURE"sa42.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa42.tif" \* MERGEFORMATINET
(第4题) (第6题) (第8题) (第9题) (第10题)
5.根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
用水量/吨 15 20 25 30 35
户数 3 6 7 9 5
则这30户家庭该月用水量的众数和中位数分别是( )
A.25,27 B.25,25 C.30,27 D.30,25
6.菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=45°,则B点的坐标是( )
A.(2+,) B.(2-,) C.(-2+,) D.(-2-,)
7.对于一次函数y=-2x+4,下列结论错误的是( )
A.若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1>y2
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得y=-2x的图象
D.函数的图象与x轴的交点坐标是(0,4)
8.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A.2.5 B. C. D.2
9.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙车前4 s行驶的路程为48 m B.在0至8 s内甲的速度每秒增加4 m/s
C.两车到第3 s时行驶的路程相等 D.在4至8 s内甲的速度都大于乙的速度
10.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共30分)
11.计算:-=________.
12.某招聘考试分笔试和面试两项,其中笔试按60%、面试按40%计算加权平均数,作为总成绩,孔西笔试成绩为90分,面试成绩为85分,那么孔西的总成绩是________分.
13.一次函数y=(3-a)x+b-2在直角坐标系中的图象如图所示,化简|b-a|--|2-b|=________.
INCLUDEPICTURE"tu23.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\tu23.tif" \* MERGEFORMATINET
(第13题) (第15题) (第16题) (第17题)
14.某超市利用五一开展促销活动,店前公告如下:一次性购买某种服装3件,每件仅售80元,如果超过3件,则超过部分打八折,顾客所付款y(元)与所购服装件数x(x≥3)之间的函数关系式为______________.
15.将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中(如图),设筷子露在杯子外面的长度为h cm,则h的取值范围是______________.
16.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,连接EF.若AB=10,则EF的长是________.
17.如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=45°,则=________.
18.如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b<x的解集为__________.
INCLUDEPICTURE"sa48.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa48.tif" \* MERGEFORMATINET
(第18题) (第19题) (第20题)
19.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的区域面积为________.
20.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为__________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.(1)计算:2+3--;
(2)已知x=2+,y=2-,求代数式·的值.
22.如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
INCLUDEPICTURE"sa51.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa51.tif" \* MERGEFORMATINET
23.已知a,b,c满足|a-|++(c-4)2=0.
(1)求a,b,c的值.
(2)判断以a,b,c为边能否构成三角形?若能构成三角形,此三角形是什么形状,并求出三角形的面积;若不能,请说明理由.
24.某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形统计图;
(2)写出这20名学生每人植树量的众数和中位数;
(2)估计这240名学生共植树多少棵.
25.如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为4的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
INCLUDEPICTURE"XT20.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\XT20.tif" \* MERGEFORMATINET
26.新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4 000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
(方案一)降价8%,另外每套房赠送a元装修基金;
(方案二)降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数解析式;
(2)老王要购买第十六层的一套房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
答案
一、1.C 2.A 3.B 4.C 5.D 6.D
7.D 点拨:k=-2<0,∴y随x的增大而减小,故A正确;k<0,b>0,图象过第一、二、四象限,B正确;函数图象向下平移4个单位长度得y=-2x的图象,C正确;函数的图象与x轴的交点坐标是(2,0),D错误.
8.B 点拨:如图,
INCLUDEPICTURE"adj115.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\adj115.tif" \* MERGEFORMATINET (第8题)
连接AC,CF,
在正方形ABCD和正方形CEFG中,
∵BC=1,CE=3,
∴AC=,CF=3.
∵∠ACD=∠GCF=45°,
∴∠ACF=45°+45°=90°.
∴△ACF是直角三角形.
由勾股定理得,AF==2.
∵H是AF的中点,∴CH=AF=.
故选B.
9.C
10.D 点拨:连接ED,如图所示.∵AD∥BC,DC∥AE,∴四边形AECD是平行四边形.又∵AD=DC,∴四边形AECD是菱形.又∵AO=CO,∴ED过点O且AC⊥ED,∠EAO=∠DAO.∵AE平分∠BAO,∴∠BAE=∠OAE.又∵∠ABE=∠AOE=90°,AE=AE,∴△BAE≌△OAE(AAS),∴AB=AO,EB=EO.∴AC=2AO=2AB.∵∠BAE=∠OAE,∠EAO=∠DAO,且易知∠BAD=90°,∴∠BAE=∠EAO=∠OAD=30°.∵四边形AECD是菱形,AD=2,∴AE=2,∴BE=1,∴AB=,且S△ADC=×AD×AB=×2BE×AB=2×BE×AB=2S△ABE.∵AB=AO,EB=EO,∴AE垂直平分BO,∴①②③④均正确.
INCLUDEPICTURE"sa54.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa54.tif" \* MERGEFORMATINET (第10题)
二、11. 12.88 13.1
14.y=64x+48(x≥3)
15.11≤h≤12
16.5 点拨:连接CD,易证四边形EFCD为平行四边形,则EF=CD,再利用直角三角形斜边上的中线等于斜边的一半即可求解.
17. 18.3<x<6
19.16 点拨:如图.
INCLUDEPICTURE"adj116a.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\adj116a.tif" \* MERGEFORMATINET (第19题)
∵点A、B的坐标分别为(1,0)、(4,0),∴AB=3.
∵∠CAB=90°,BC=5,
∴由勾股定理可得AC=4,∴A′C′=4.
∵点C′在直线y=2x-6上,
∴2x-6=4,解得x=5.
即OA′=5.∴CC′=5-1=4,
∴S BCC′B′=4×4=16,
即线段BC扫过的区域面积为16.
故答案为16.
20.(2.5,4)或(3,4)或(2,4)或(8,4) 点拨:∵四边形OABC是矩形,点A坐标为(10,0),点C坐标为(0,4),
∴∠OCB=90°,OC=4,BC=OA=10.∵D为OA的中点,∴OD=AD=5.①当PO=PD时,如图①,点P在OD的垂直平分线上,∴点P的坐标为(2.5,4);②当OP=OD时,如图②所示,则OP=OD=5,PC==3,∴点P的坐标为(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3.分两种情况:当E在D的左侧时,如图③所示,OE=5-3=2,∴点P的坐标为(2,4);当E在D的右侧时,如图④所示,OE=5+3=8,∴点P的坐标为(8,4).综上所述:点P的坐标为(2.5,4)或(3,4)或(2,4)或(8,4).
INCLUDEPICTURE"sa55.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\sa55.tif" \* MERGEFORMATINET (第20题)
三、21.解:(1)原式=4+3×--×4=4+2-4=2.
(2)原式=·=·=-.
当x=2+,y=2-时,
原式=-=-4.
22.解:(1)把(-2,-1),(1,3)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=x+.
(2)把x=0代入y=x+得y=,
∴D点的坐标为,
∴S△AOB=S△AOD+S△BOD=××2+××1=.
23.解:(1)∵a,b,c满足|a-|++(c-4)2=0,
∴|a-|=0,=0,(c-4)2=0,解得a=,b=5,c=4.
(2)∵a=,b=5,c=4,
∴a+b=+5>4,
∴以a,b,c为边能构成三角形.
∵a2+b2=()2+52=32=(4)2=c2,
∴此三角形是直角三角形.
∴S=××5=.
24.解:(1)D类的人数为:20-4-8-6=2.补全条形统计图略.
(2)由图可知,植树5棵的人数最多,所以,众数为5.按照植树的棵数从少到多排列,第10人与第11人都是植5棵树,所以,中位数是5.
(3)x==5.3(棵),240×5.3=1 272(棵).
答:估计这240名学生共植树1 272棵.
25.(1)证明:∵CE∥AD且CE=AD,
∴四边形ADCE是平行四边形.
∵在△ABC中,AB=AC,AD平分∠BAC,∴AD⊥BC(等腰三角形三线合一),∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)解:∵△ABC是等边三角形,边长为4,AD平分∠BAC,∴AC=BC=4=2CD,∠DAC=30°.∴CD=2.又∵CE∥AD,∴∠ACE=∠DAC=30°.∵四边形ADCE是矩形,∴AE=CD=2,OC=OA=AC=2,∠AEC=90°,∴CE===2.
∵FC=CO,∴FC=2.
如图,过O作OH⊥CE于H,
∵∠ACE=30°,∴OH=OC=1,
∴S四边形AOFE=S△AEC-S△COF=×2×2-×2×1=2-1.
INCLUDEPICTURE"XT22.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\下册word\\八下人典中点\\XT22.tif" \* MERGEFORMATINET (第25题)
26.解:(1)当1≤x≤8时,y=4 000-30(8-x)=4 000-240+30x=30x+3 760;
当9≤x≤23时,y=4 000+50(x-8)=4 000+50x-400=50x+3 600.
∴所求函数解析式为
y=
(2)当x=16时,
方案一每套房总费用为w1=120×(50×16+3 600)×(1-8%)-a=485 760-a(元).
方案二每套房总费用为w2=120×(50×16+3 600)×(1-10%)=475 200(元).
∴当w1<w2,即485 760-a<475 200时,a>10 560;
当w1=w2,即485 760-a=475 200时,a=10 560;
当w1>w2,即485 760-a>475 200时,a<10 560.
因此当每套房赠送装修基金多于10 560元时,选择方案一合算;
当每套房赠送装修基金等于10 560元时,两种方案一样;
当每套房赠送装修基金少于10 560元时,选择方案二合算.
同课章节目录
