2025年广东省深圳市中考数学真题试卷(含答案)
文档属性
| 名称 | 2025年广东省深圳市中考数学真题试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 13:40:04 | ||
图片预览




文档简介
广东省深圳市2025届中考数学试卷
说明:本卷共6页。考试时间90分钟,满分100分。答题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码。考试结束后,请将本卷和答题卡一并上交。
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.节约水5吨记作+5吨,则浪费水2吨记作
A.-3吨 B.+2吨 C.-2吨 D.+3吨
2.如图为出现在深圳街头的新型无线充电石墩,关于石墩的三视图的描述,正确的是
A.主视图和左视图相同 B.主视图和俯视图相同
C.左视图和俯视图相同 D.三个视图都相同
3.某校进行《九章算术》,《周髀算经》,《孙子算经》,《算法统宗》四本书的长文本阅读活动,小聪从中任取一本,恰好抽到《九章算术》的概率为
A. B. C. D.
4.如图为人行天桥的示意图,若高长为10米,斜道长为30米,则的值为
A. B.3 C. D.
5.下列计算正确的是
A. B. C. D.
6.如图为小颖在试鞋镜前的光路图,入射光线经平面镜后反射入眼,若,,,则入射角的度数为
A.22° B.32° C.35° D.122°
7.某社区植树60棵,实际种植人数是原计划人数的2倍,实际平均每人种植棵树比原计划少了3棵。若设原计划人数为人,则下列方程正确的是
A. B. C. D.
8.如图,将正方形沿折叠,使得点与对角线的交点重合,为折痕,则的值为
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
9.若关于的方程的解为,则__________。
10.如图,将无人机沿着轴向右平移3个单位,若无人机上一点的坐标为(1,2),则平移后点的坐标为__________。
11.计算:__________。
12.如图,同一平面直角坐标系下的正比例函数与反比例函数相交于点和点。若的横坐标为1,则的坐标为__________。
13.如图,以矩形的点为圆心,的长为半径作,交于点,点为上一点,连接,将线段绕点顺时针旋转至,点落在上,且点为中点。若,,则的长为__________。
三、解答题(本题共7小题,共61分)
14.(6分)计算:。
15.(7分)解一元一次方程组,并在数轴上表示。
解:由不等式①得:__________,
由不等式②得:__________,
在数轴上表示为:
所以,原不等式组的解集为__________。
16.(8分)某班级拟开展科技主题班会活动,现从“科技安全”,“科技畅想”,“科技生活”,“科技前沿”,“科技故事”中挑选一个主题。全班同学通过投票选出最受欢迎的主题,投票结果的条形统计图与扇形统计图如下:
请根据以上信息,完成下列问题:
(1)本次投票共__________人参与,其中科技安全所占百分比为__________,并补全条形统计图。(3分)
(2)为确定班会科技主题,从该班选择7名学生代表为“科技畅想”和“科技故事”打分,分数列表如下:
科技畅想 10 9 9 3 6 9 10
科技故事 9 10 7 8 6 8 8
平均数 中位数 众数
科技畅想 9
科技故事 8 8 c
求表中的数据:________,________,________。(3分)
(3)结合上述信息,应该选择哪个科技主题,并说明理由。(2分)
17.(8分)某学校采购体育用品,需要购买三种球类。已知某体育用品商店排球的单价为30元/个,篮球,足球的价格如下表:
①篮球、足球、排球各买一个的价格为140元
②购买2个足球的价格比购买一个篮球多花费40元
③购买5个篮球与购买6个足球花费相同
(1)请你从上述3个条件中任选2个作为条件,求出篮球和足球的单价;
(2)若该学校要购买篮球,足球共10个,且足球的个数不超过篮球个数的2倍,请问购买多少个篮球时,花费最少,最少费用是多少
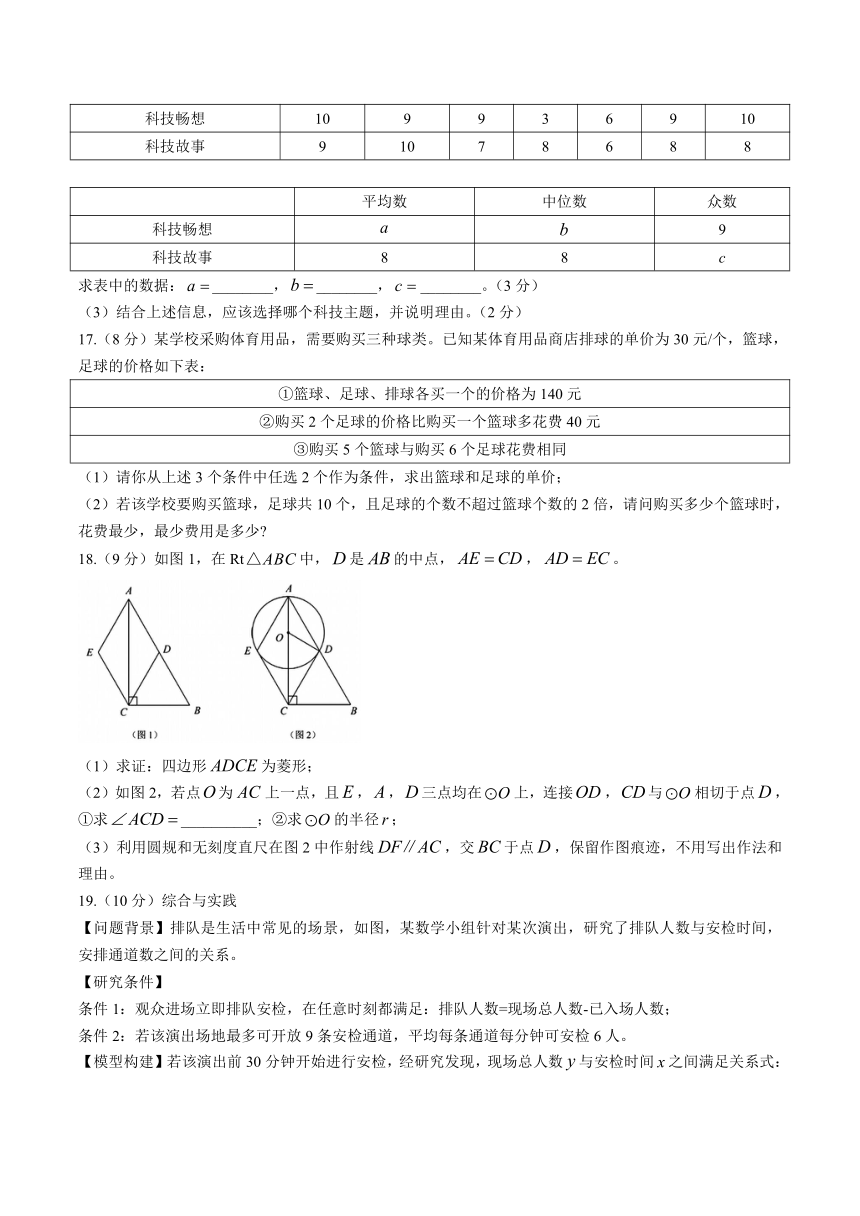
18.(9分)如图1,在Rt中,是的中点,,。
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,且,,三点均在上,连接,与相切于点,①求__________;②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由。
19.(10分)综合与实践
【问题背景】排队是生活中常见的场景,如图,某数学小组针对某次演出,研究了排队人数与安检时间,安排通道数之间的关系。
【研究条件】
条件1:观众进场立即排队安检,在任意时刻都满足:排队人数=现场总人数-已入场人数;
条件2:若该演出场地最多可开放9条安检通道,平均每条通道每分钟可安检6人。
【模型构建】若该演出前30分钟开始进行安检,经研究发现,现场总人数与安检时间之间满足关系式:
结合上述信息,请完成下述问题:
(1)当开通3条安检通道时,安检时间分钟时,已入场人数为__________,排队人数与安检时间的函数关系式为_________.
【模型应用】
(2)在(1)的条件下,排队人数在第几分钟达到最大值,最大人数为多少?
(3)已知该演出主办方要求:
①排队人数在安检开始10分钟内(包含10分钟)减少;
②尽量少安排安检通道,以节省开支。
若同时满足以上两个要求,可开设几条安检通道,请说明理由
【总结反思】
函数可刻画生活实际场景,但要注意验证模型的正确性,未来可结合更多变量(如突发情况、安检流程优化等)进行更深入的分析,以提高模型的准确性和实用性。
20.(12分)综合与探究
【探索发现】如图1,小军用两个大小不同的等腰直角三角板拼接成一个四边形。
【抽象定义】以等腰三角形为边向外作等腰三角形,使该边所对的的角等于原等腰三角形的顶角,此时该四边形称为“双等四边形”,原等腰三角形称为四边形的“伴随三角形”。如图2,在中,,,。此时,四边形是“双等四边形”,是“伴随三角形”。
【问题解决】如图3,在四边形中,,,。
求:①与的位置关系为:__________:②_____。(填“>”,“”或“”)
【方法应用】①如图4,将绕点逆时针旋转至,点恰好落在边上,求证:四边形是双等四边形。
②如图5,在等腰三角形中,,,,在平面内找一点,使四边形是以为伴随三角形的双等四边形,若存在,请求出的长,若不存在,请说明理由。
数学参考答案 2025.6.27
说明:全卷共6页。考试时间90分钟,满分100分。答题前,请将姓名、准考证号、考点用黑色字迹的钢笔或签字笔写在答题卡指定的位置上,并将条形码粘贴好。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(24分)
1 2 3 4 5 6 7 8
B A C D B B A D
二、填空题(15分)
9 10 11 12 13
4 (4,2) a-1 (-1,-1) 6
三、解答题(61分)
14.(6分)计算:
原式
15.(7分)解不等式组,并在数轴上把解集表示出来。
解不等式①,得:
解不等式②,得:
所以不等式组的解集为:
在数轴上表示如下:
16.(1)50
(2)8 9 8
(3)选择科技故事主题;理由是该主题极差比较小,(该题属于开放试题,言之有理即可)
17.解:(1)设每个篮球元,每个足球元
(三个方程组任选一种即可)
解得:
答:每个篮球60元,每个足球50元。
(2)设蓝球有个,则足球有个
解得:
设购买的总费用是元
随着的减小而减小
当m最小值为4时,最小值为540元
答:当购买篮球4个的时候,所花费用最少。
18.解:(1),
四边形ADCE为平行四边形
又,且为中点
平行四边形为菱形.
(2)①四边形为菱形.
又
切于
②设半径为
解得:
(3)示例:
19.(10分)排队
【研究条件】1.始终存在条件:排队人数=现场总人数-已入场人数。
2.最多设置9条安检通道,每条通道平均每分钟进6人.演唱开始前30分钟,现场安检期间现场总人数与安检时间大约存在函数
表达式:
(1)若开设3条安检通道,安检时间为分钟,则已入场人数为(用表示),若排队人数为,则与的函数表达式
(2)在(1)的条件下,当安检时间在第几分钟时,排队人数达到最大值?最大值为多少
当时,
(3)主办方要求:①排队人数在10分钟内(包含10分钟)减少:
②安检通道尽可能少,节约成本.你认为应该设置多少条安检通道并说明理由(4分)
设开了条通道则:对称轴为
∵排队人数10分钟(包括10分钟)内减少
,即:
又最多开通9条
为正整数,最小值为7 最少开7条通道
【研究反思】要结合实际。
20.(1)因为:;
(2)为旋转得到
令,则,
又
四边形为双等四边形
(3)作于点
,
,
设.则:
在中,,即.
解得:
,
若,时,
②若,时,
作于点
③若,时,
③若,时,
综上所述:满足条件时,或或
说明:本卷共6页。考试时间90分钟,满分100分。答题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码。考试结束后,请将本卷和答题卡一并上交。
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.节约水5吨记作+5吨,则浪费水2吨记作
A.-3吨 B.+2吨 C.-2吨 D.+3吨
2.如图为出现在深圳街头的新型无线充电石墩,关于石墩的三视图的描述,正确的是
A.主视图和左视图相同 B.主视图和俯视图相同
C.左视图和俯视图相同 D.三个视图都相同
3.某校进行《九章算术》,《周髀算经》,《孙子算经》,《算法统宗》四本书的长文本阅读活动,小聪从中任取一本,恰好抽到《九章算术》的概率为
A. B. C. D.
4.如图为人行天桥的示意图,若高长为10米,斜道长为30米,则的值为
A. B.3 C. D.
5.下列计算正确的是
A. B. C. D.
6.如图为小颖在试鞋镜前的光路图,入射光线经平面镜后反射入眼,若,,,则入射角的度数为
A.22° B.32° C.35° D.122°
7.某社区植树60棵,实际种植人数是原计划人数的2倍,实际平均每人种植棵树比原计划少了3棵。若设原计划人数为人,则下列方程正确的是
A. B. C. D.
8.如图,将正方形沿折叠,使得点与对角线的交点重合,为折痕,则的值为
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
9.若关于的方程的解为,则__________。
10.如图,将无人机沿着轴向右平移3个单位,若无人机上一点的坐标为(1,2),则平移后点的坐标为__________。
11.计算:__________。
12.如图,同一平面直角坐标系下的正比例函数与反比例函数相交于点和点。若的横坐标为1,则的坐标为__________。
13.如图,以矩形的点为圆心,的长为半径作,交于点,点为上一点,连接,将线段绕点顺时针旋转至,点落在上,且点为中点。若,,则的长为__________。
三、解答题(本题共7小题,共61分)
14.(6分)计算:。
15.(7分)解一元一次方程组,并在数轴上表示。
解:由不等式①得:__________,
由不等式②得:__________,
在数轴上表示为:
所以,原不等式组的解集为__________。
16.(8分)某班级拟开展科技主题班会活动,现从“科技安全”,“科技畅想”,“科技生活”,“科技前沿”,“科技故事”中挑选一个主题。全班同学通过投票选出最受欢迎的主题,投票结果的条形统计图与扇形统计图如下:
请根据以上信息,完成下列问题:
(1)本次投票共__________人参与,其中科技安全所占百分比为__________,并补全条形统计图。(3分)
(2)为确定班会科技主题,从该班选择7名学生代表为“科技畅想”和“科技故事”打分,分数列表如下:
科技畅想 10 9 9 3 6 9 10
科技故事 9 10 7 8 6 8 8
平均数 中位数 众数
科技畅想 9
科技故事 8 8 c
求表中的数据:________,________,________。(3分)
(3)结合上述信息,应该选择哪个科技主题,并说明理由。(2分)
17.(8分)某学校采购体育用品,需要购买三种球类。已知某体育用品商店排球的单价为30元/个,篮球,足球的价格如下表:
①篮球、足球、排球各买一个的价格为140元
②购买2个足球的价格比购买一个篮球多花费40元
③购买5个篮球与购买6个足球花费相同
(1)请你从上述3个条件中任选2个作为条件,求出篮球和足球的单价;
(2)若该学校要购买篮球,足球共10个,且足球的个数不超过篮球个数的2倍,请问购买多少个篮球时,花费最少,最少费用是多少
18.(9分)如图1,在Rt中,是的中点,,。
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,且,,三点均在上,连接,与相切于点,①求__________;②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由。
19.(10分)综合与实践
【问题背景】排队是生活中常见的场景,如图,某数学小组针对某次演出,研究了排队人数与安检时间,安排通道数之间的关系。
【研究条件】
条件1:观众进场立即排队安检,在任意时刻都满足:排队人数=现场总人数-已入场人数;
条件2:若该演出场地最多可开放9条安检通道,平均每条通道每分钟可安检6人。
【模型构建】若该演出前30分钟开始进行安检,经研究发现,现场总人数与安检时间之间满足关系式:
结合上述信息,请完成下述问题:
(1)当开通3条安检通道时,安检时间分钟时,已入场人数为__________,排队人数与安检时间的函数关系式为_________.
【模型应用】
(2)在(1)的条件下,排队人数在第几分钟达到最大值,最大人数为多少?
(3)已知该演出主办方要求:
①排队人数在安检开始10分钟内(包含10分钟)减少;
②尽量少安排安检通道,以节省开支。
若同时满足以上两个要求,可开设几条安检通道,请说明理由
【总结反思】
函数可刻画生活实际场景,但要注意验证模型的正确性,未来可结合更多变量(如突发情况、安检流程优化等)进行更深入的分析,以提高模型的准确性和实用性。
20.(12分)综合与探究
【探索发现】如图1,小军用两个大小不同的等腰直角三角板拼接成一个四边形。
【抽象定义】以等腰三角形为边向外作等腰三角形,使该边所对的的角等于原等腰三角形的顶角,此时该四边形称为“双等四边形”,原等腰三角形称为四边形的“伴随三角形”。如图2,在中,,,。此时,四边形是“双等四边形”,是“伴随三角形”。
【问题解决】如图3,在四边形中,,,。
求:①与的位置关系为:__________:②_____。(填“>”,“”或“”)
【方法应用】①如图4,将绕点逆时针旋转至,点恰好落在边上,求证:四边形是双等四边形。
②如图5,在等腰三角形中,,,,在平面内找一点,使四边形是以为伴随三角形的双等四边形,若存在,请求出的长,若不存在,请说明理由。
数学参考答案 2025.6.27
说明:全卷共6页。考试时间90分钟,满分100分。答题前,请将姓名、准考证号、考点用黑色字迹的钢笔或签字笔写在答题卡指定的位置上,并将条形码粘贴好。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(24分)
1 2 3 4 5 6 7 8
B A C D B B A D
二、填空题(15分)
9 10 11 12 13
4 (4,2) a-1 (-1,-1) 6
三、解答题(61分)
14.(6分)计算:
原式
15.(7分)解不等式组,并在数轴上把解集表示出来。
解不等式①,得:
解不等式②,得:
所以不等式组的解集为:
在数轴上表示如下:
16.(1)50
(2)8 9 8
(3)选择科技故事主题;理由是该主题极差比较小,(该题属于开放试题,言之有理即可)
17.解:(1)设每个篮球元,每个足球元
(三个方程组任选一种即可)
解得:
答:每个篮球60元,每个足球50元。
(2)设蓝球有个,则足球有个
解得:
设购买的总费用是元
随着的减小而减小
当m最小值为4时,最小值为540元
答:当购买篮球4个的时候,所花费用最少。
18.解:(1),
四边形ADCE为平行四边形
又,且为中点
平行四边形为菱形.
(2)①四边形为菱形.
又
切于
②设半径为
解得:
(3)示例:
19.(10分)排队
【研究条件】1.始终存在条件:排队人数=现场总人数-已入场人数。
2.最多设置9条安检通道,每条通道平均每分钟进6人.演唱开始前30分钟,现场安检期间现场总人数与安检时间大约存在函数
表达式:
(1)若开设3条安检通道,安检时间为分钟,则已入场人数为(用表示),若排队人数为,则与的函数表达式
(2)在(1)的条件下,当安检时间在第几分钟时,排队人数达到最大值?最大值为多少
当时,
(3)主办方要求:①排队人数在10分钟内(包含10分钟)减少:
②安检通道尽可能少,节约成本.你认为应该设置多少条安检通道并说明理由(4分)
设开了条通道则:对称轴为
∵排队人数10分钟(包括10分钟)内减少
,即:
又最多开通9条
为正整数,最小值为7 最少开7条通道
【研究反思】要结合实际。
20.(1)因为:;
(2)为旋转得到
令,则,
又
四边形为双等四边形
(3)作于点
,
,
设.则:
在中,,即.
解得:
,
若,时,
②若,时,
作于点
③若,时,
③若,时,
综上所述:满足条件时,或或
同课章节目录
