专题3图形与几何-2025年小升初数学暑假专项提升(沪教版)(含解析)
文档属性
| 名称 | 专题3图形与几何-2025年小升初数学暑假专项提升(沪教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 431.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览




文档简介
专题3:图形与几何
1.爸爸将净含量为625毫升的一瓶饮料浸没在一个装满水的盆里,盆里溢出的水( )。
A.是625毫升 B.比625毫升多 C.不足625毫升 D.无法确定
2.如图,求CD长度正确的是( )。(单位:dm)
A.5×4÷3 B.3×4÷5 C.5×3÷4 D.5×3×4
3.平行四边形的高有( )条。
A.1 B.2 C.4 D.无数
4.一个长方体中,如果有四个面的面积相等,其余两个面( )。
A.都是长方形 B.都是正方形 C.一个是长方形,一个是正方形 D.不能确定
5.从长7分米、宽6分米、高3分米的长方体中切出一个表面积最大的正方体,该正方体的棱长总和是( )分米。
A.36 B.64 C.72 D.84
6.下图是一个直角三角形和一个正方形组成的梯形,已知直角三角形的面积是15平方厘米,那么梯形的高是( )厘米,面积是( )平方厘米。
A.6;51 B.112;16.5 C.3;33 D.33;51
7.两个( )的梯形可以拼成一个平行四边形。
A.形状相同 B.等底等高 C.完全一样 D.大小相等
8.三角形和平行四边形面积相等,平行四边形的底是三角形底的2倍,若平行四边形的高是4厘米,则三角形的高是( )。
A.2厘米 B.4厘米 C.8厘米 D.16厘米
9.如图,MN是平行四边形DC边上的( ),边DC叫做平行四边形的( )。
10.有两个完全相同的直角三角形,三条边长分别为6cm、8cm和10cm,用它们可以拼出( )种不同的平行四边形,这个三角形斜边上的高是( )cm。
11.一个等腰梯形的周长是40分米,高是5分米,一条腰长8分米,这个等腰梯形的面积是( )平方分米。
12.用一根长72厘米的铁丝做长方体框架,已知长是宽的3倍,宽是高的2倍,这个长方体的体积是( )立方厘米。
13.一个正方体的棱长4分米,它的棱长之和是( )分米,它的表面积为( )平方分米。
14.如图,一个正方体的展开图,2号面相对的是( )号面;4号面相对的是( )号面。
15.单位换算。
0.2m2=( )cm2 ( )dm3( )cm3=6.051dm3
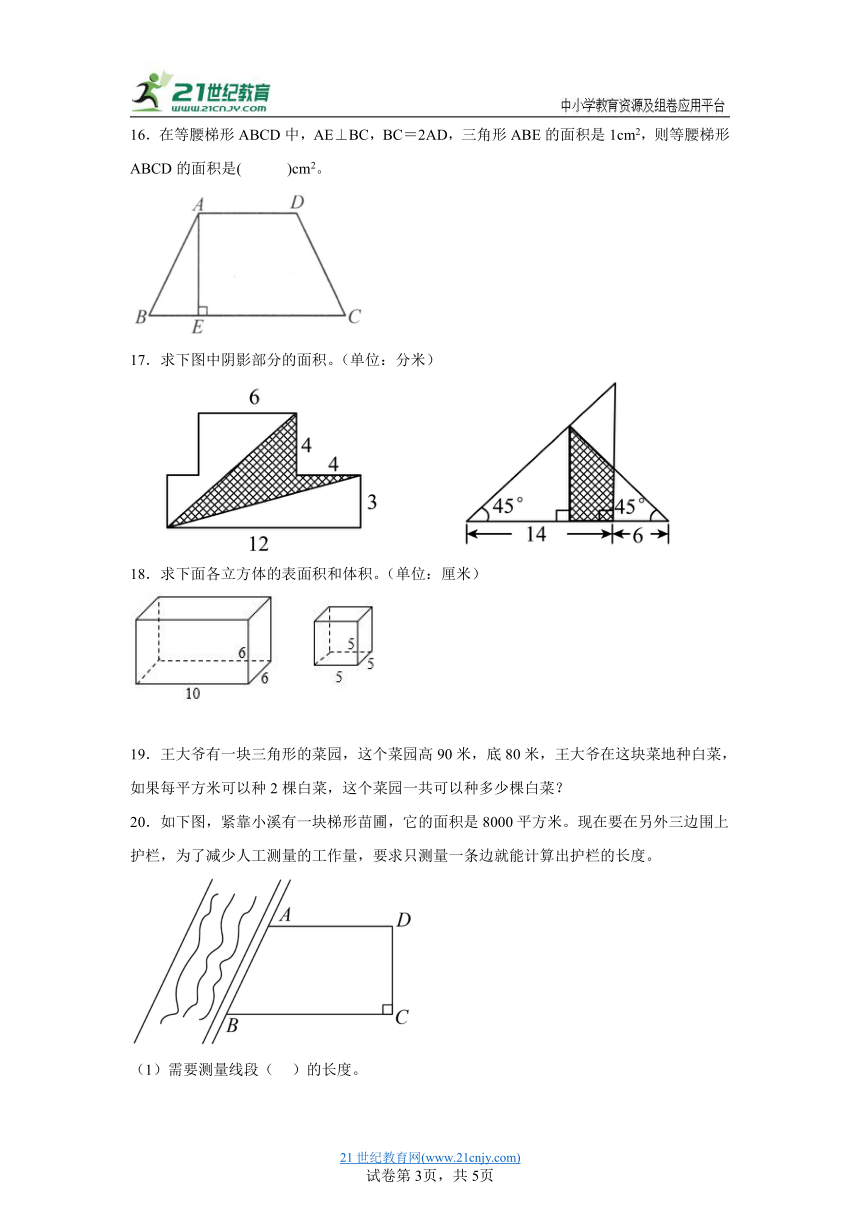
16.在等腰梯形ABCD中,AE⊥BC,BC=2AD,三角形ABE的面积是1cm2,则等腰梯形ABCD的面积是( )cm2。
17.求下图中阴影部分的面积。(单位:分米)
18.求下面各立方体的表面积和体积。(单位:厘米)
19.王大爷有一块三角形的菜园,这个菜园高90米,底80米,王大爷在这块菜地种白菜,如果每平方米可以种2棵白菜,这个菜园一共可以种多少棵白菜?
20.如下图,紧靠小溪有一块梯形苗圃,它的面积是8000平方米。现在要在另外三边围上护栏,为了减少人工测量的工作量,要求只测量一条边就能计算出护栏的长度。
(1)需要测量线段( )的长度。
(2)如果测出这条线段长50米,那么护栏的长度是多少米?
21.外卖给我们的生活带来了很大的便利,这种便利离不开外卖人员的辛苦付出。淘气的叔叔是一个外卖骑手,下图是他的外卖保温包的示意图,做一个这样的保温包至少需要多少平方厘米的材料?(重叠部分忽略不计)
22.一块棱长是80厘米的正方体的铁块,现在要把它溶解成一个横截面积是40平方厘米的长方体,这个长方体的长是多少厘米?请你分析小胖的解题过程的错误点在哪里。并在下面写出正确的解题过程:
23.如图是全运会济南赛区奥体中心游泳馆的主游泳池,它长50米、宽25米、深2米。
(1)建造奥体中心游泳池至少需要挖土多少立方米?
(2)如果要给这个游泳池注1.8米深的水,已知每小时能注水150立方米。需要几小时注完?
24.一个直角梯形,如果把上底延长5cm,下底延长2cm,高不变,面积就增加了28cm2,而且变成一个正方形,求原来直角梯形的面积。
25.如图,在直角梯形ABCD中,AD=DC=12cm,三角形ABE的面积是24cm2,求三角形BDF的面积。
26.一个长方体的玻璃缸,从里面量长,宽,高,水深。如果投入一块棱长为的正方体铁块(如图),缸里的水溢出多少升?
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《专题3 图形与几何- 2025年小升初数学暑假专项提升(沪教版)》参考答案:
1.B
【分析】净含量为625毫升,所以625毫升是瓶子里饮料的体积,那么饮料瓶子的体积必定大于625毫升,由此解答。
【详解】根据分析可知,盆里溢出的水比625毫升多。
故答案为:B
【点睛】本题主要考查学生对体积概念的认识。
2.C
【分析】“平行四边形的面积=底×高”,底和高必须是相对应的,用5×3求出平行四边形的面积,再除以4即可求出其相对应的底CD。
【详解】求CD长度,列式为:5×3÷4;
故答案为:C。
【点睛】熟记平行四边形的面积公式是解答本题的关键。
3.D
【分析】从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。据此可知,平行四边形有两组高,无数条高;据此解答。
【详解】根据平行四边形高的意义可知:平行四边形的高有无数条。
故答案为:D
4.B
【分析】当长方体有相对的两个面是正方形时,其余四个面都是完全一样的长方形,反之,当长方体有4个面的面积相等,其余两个面一定是正方形,由此解决问题。
【详解】当长方体有4个面的面积相等,说明这四个面的长和宽是一样的,一定有四条边相等,即其余两个面是正方形。
故答案选:B
【点睛】此题主要是利用长方体的面的特征:长方体有六个面,每一个面都是长方形(特殊情况有相对的两个面是正方形)来解决问题。
5.A
【分析】从长7分米、宽6分米、高3分米的长方体中切出一个表面积最大的正方体,那么正方体的棱长是长方体的高3分米,根据正方体的棱长总和=棱长×12,代入数据计算即可。
【详解】3<6<7
最大的正方体的棱长是3分米。
正方体的棱长总和:3×12=36(分米)
故答案为:A
【点睛】明确在长方体中切出一个最大的正方体,那么正方体的棱长是长方体最小的棱长。
6.A
【分析】观察图形可知,梯形高等于三角形的高也就是正方形的边长,已知三角形面积和底,根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出三角形的高,进而求出梯形的上底、下底和高的长度,再根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
【详解】梯形的高:15×2÷5
=30÷5
=6(厘米)
梯形面积:(6+6+5)×6÷2
=(12+5)×6÷2
=17×6÷2
=102÷2
=51(平方厘米)
故答案为:A
【点睛】本题也可以利用正方形面积加上三角形面积的和求出梯形面积。
7.C
【分析】根据梯形和平行四边形的关系,直接解题即可。
【详解】两个完全一样的梯形可以拼成一个平行四边形。
故答案为:C
【点睛】本题考查了梯形和平行四边形的关系,明确两个图形的特征是解题的关键。
8.D
【分析】三角形的面积=底×高÷2,平行四边形的面积=底×高,平行四边形的底是三角形底的2倍,则三角形的高是平行四边形的高的4倍,据此解答即可。
【详解】若平行四边形的高是4厘米,则三角形的高是4×4=16厘米。
故答案为:D。
【点睛】本题考查三角形、平行四边形的面积,解答本题的关键是掌握三角形、平行四边形的面积的计算公式。
9. 高 底
【分析】根据平行四边形高的含义:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高;据此解答即可。
【详解】由分析可得:MN是平行四边形DC边上的高,边DC叫做平行四边形的底。
【点睛】此题考查了平行四边形高的含义,应注意灵活运用。
10. 3 4.8
【分析】由于两个完全相同的直角三角形三条边分别是6cm、8cm、10cm,即三条边长度不同,因此可以分别用三条边作公共边来拼,这样可以拼出3种不同的平行四边形;
根据三角形面积公式:面积=底×高÷2,用直角三角形两条直角边做为底和高,求出这个三角形的面积,再利用高=面积×2÷底,即可求出斜边商的高的长度。
【详解】根据分析可知,可以拼出3种不同的平行四边形;
6×8÷2×2÷10
=48÷2×2÷10
=24×2÷10
=48÷10
=4.8(cm)
有两个完全相同的直角三角形,三条边长分别为6cm、8cm和10cm,用它们可以拼出3种不同的平行四边形,这个三角形斜边上的高是4.8cm。
【点睛】本题考察图形的拼组以及三角形面积公式的灵活运用。
11.60
【分析】根据等腰梯形的特征可知,等腰梯形的两条腰相等,用等腰梯形的周长-8×2,求出梯形的上底与下底的和,再根据梯形面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
【详解】(40-8×2)×5÷2
=(40-16)×5÷2
=24×5÷2
=120÷2
=60(平方分米)
一个等腰梯形的周长是40分米,高是5分米,一条腰长8分米,这个等腰梯形的面积是60平方分米。
【点睛】熟练掌握等腰梯形的特征以及梯形面积公式是解答本题的关键。
12.96
【分析】根据题意可知,长是宽的3倍,宽是高的2倍,则可以设高为x厘米,宽为2x厘米,长为(3×2x)厘米,根据长方体棱长和=(长+宽+高)×4,列方程为(3×2x+2x+x)×4=72,然后解出方程,进而求出宽和长,最后根据长方体的体积=长×宽×高,代入数据解答。
【详解】解:设高为x厘米,宽为2x厘米,长为(3×2x)厘米。
(3×2x+2x+x)×4=72
(6x+2x+x)×4=72
9x×4=72
36x=72
36x÷36=72÷36
x=2
宽:2×2=4(厘米)
长:4×3=12(厘米)
12×4×2=96(立方厘米)
这个长方体的体积是96立方厘米。
【点睛】本题主要考查了长方体棱长和公式、长方体体积公式的灵活应用,可列方程解决问题。
13. 48 96
【分析】已知正方体的棱长,求正方体的棱长总和,用公式:正方体的棱长总和=棱长×12,正方体的表面积=棱长×棱长×6,据此列式解答。
【详解】4×12=48(分米)
4×4×6
=16×6
=96(平方分米)
【点睛】此题考查了正方体的棱长总和和表面积的计算,牢记公式认真计算即可。
14. 4 2
【分析】
根据正方体的展开图知识,属于“1-3-2型”,折成正方体后,有公共边的两个面相邻,没有公共边的两个面相对。1号面相对的是5号面;2号面相对的是4号面,3号面相对的是6号面。
【详解】由分析可知:
如图,一个正方体的展开图,2号面相对的是4号面;4号面相对的是2号面。
15. 2000 6 51
【分析】根据1=10000,1=1000,高级单位化低级单位乘进率,低级单位化高级单位除以进率解答。
【详解】0.2×10000=2000(),所以0.2=2000;
因为0.051×1000=51(),所以6.051=651。
16.6
【分析】由S梯形=(上底+下底)×高÷2得,S梯形ABCD=(AD+BC)×AE÷2,因为BC=2AD,所以S梯形ABCD=3AD×AE÷2=1.5AD×AE,据此解答。
【详解】
过A作AF∥CD,交BC于F
由题意可知,AB=CD=AF
则三角形ABF为等腰三角形
S△ABF=2S△ABE=1×2=2(cm2)
S△ABF=BF×AE÷2=2(cm2)
BF×AE=4(cm2)
由图可知,AD=BF=FC
则AD×AE=4(cm2)
S梯形ABCD=1.5×4=6(cm2)
【点睛】作辅助线把三角形ABE的面积转化为梯形ABCD的面积是解答本题的关键。
17.(1)22平方分米;
(2)32平方分米
【分析】(1)将阴影部分两个三角形,其中有一个三角形的底为4分米、高3分米;另一个三角形的底4分米、高(12-4)分米,分别计算面积,再相加即可;
(2)根据等腰直角三角形的特点,分别求出梯形(阴影部分)的上底、下底和高,其中梯形的上底是6,根据直角三角形斜边上的高等于斜边的一半可得,梯形的下底是14与6的和的一半,再用减法得出高,然后根据梯形的面积计算公式求解。
【详解】(1)4×3÷2+4×(12-4)÷2
=6+4×8÷2
=6+16
=22(平方分米)
则阴影部分的面积22平方分米。
(2)(14+6)÷2
=20÷2
=10(分米)
梯形的高:14-10=4(分米)
阴影部分的面积:
(6+10)×4÷2
=16×4÷2
=32(平方分米)
则阴影部分的面积32平方分米。
18.长方体:312平方厘米;360立方厘米。
正方体:150平方厘米;125立方厘米。
【分析】已知题目里的长方体、正方体均为一般情形,故可直接套用公式计算。
S长方体=(长×宽+高×宽+长×高)×2;
V长方体=长×宽×高
S正方体=棱长×棱长×6
V正方体=棱长×棱长×棱长
【详解】(1)(10×6+10×6+6×6)×2
=(60+60+36)×2
=156×2
=312(平方厘米)
10×6×6
=60×6
=360(立方厘米)
(2)5×5×6
=25×6
=150(平方厘米)
5×5×5
=25×5
=125(立方厘米)
19.7200棵
【分析】根据“三角形的面积=底×高÷2”求出这个菜园的面积,一共可以种白菜的棵数=菜园的面积×每平方米可以种白菜的棵数,据此解答。
【详解】90×80÷2×2
=7200÷2×2
=3600×2
=7200(棵)
答:这个菜园一共可以种7200棵白菜。
【点睛】掌握三角形的面积计算公式是解答题目的关键。
20.(1)CD
(2)370米
【分析】(1)由于要计算护栏的长度,相当于:上底(AD线段)+下底(BC线段)+高(CD线段),根据梯形的面积公式:(上底+下底)×高÷2,由于面积已知,如果知道高的长度(即CD线段),那么可以求出上底AD线段加下底BC线段的和,只需要测量一个长度即可,所以测量CD线段的长度。
(2)由于测出这条线段长是50米,也就相当于高是50米,根据梯形的面积公式:面积×2÷高=(上底+下底),把数代入即可求解,之后再把上底和下底还有高这三个线段长度相加即可求出护栏的长度。
【详解】(1)根据梯形面积公式,如果知道梯形的高(CD线段),即可求出上底(AD线段)和下底(BC线段)的和,由此即可知测量CD线段的长。
(2)8000×2÷50
=16000÷50
=320(米)
320+50=370(米)
答:护栏的长共是370米。
【点睛】本题主要考查梯形的面积公式,熟练掌握梯形的面积公式并灵活运用。
21.10138平方厘米
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(50×37+50×37+37×37)×2即可求出做一个这样的保温包至少需要的材料面积。
【详解】(50×37+50×37+37×37)×2
=(1850+1850+1369)×2
=5069×2
=10138(平方厘米)
答:做一个这样的保温包至少需要10138平方厘米的材料。
22.12800厘米;小胖把横截面积看作横截面的周长来计算
【分析】把正方体铁块溶解成一个长方体铁块,体积不变;根据正方体的体积=棱长×棱长×棱长,用80×80×80即可求出铁块的体积,然后根据长方体=横截面积×长,用铁块的体积除以横截面积,即可求出长方体的长;小胖用40÷4,显然是把40的数据当作横截面的周长,然后根据正方形的周长公式求出边长,显然这种算法是错误的。
【详解】80×80×80÷40
=512000÷40
=12800(厘米)
答:这个长方体的长是12800厘米;小胖的解题过程是错的,因为他把横截面积看作横截面的周长来计算。
【点睛】本题主要考查了正方体体积公式和长方体体积公式的灵活应用。
23.(1)2500立方米
(2)15小时
【分析】(1)要求建造奥体中心游泳池至少需要挖土多少立方米,把这个中心游泳池看作一个无盖的长方体,相当于求这个长方体的体积,根据长方体的体积=长×宽×高,代入数值计算即可解答。
(2)根据长方体的体积公式,求出注入的水的总体积,再除以150,所得结果即为需要几小时注完。
【详解】(1)50×25×2=2500(立方米)
答:建造奥体中心游泳池至少需要挖土2500立方米。
(2)50×25×1.8÷150
=2250÷150
=15(小时)
答:需要15小时注完。
24.36cm2
【分析】一个直角梯形,如果把上底延长5cm,下底延长2cm,高不变,面积就增加了28cm2,而且变成一个正方形,说明增加部分是一个上底为2厘米,下底为5厘米,高不变的直角梯形,再根据高=梯形面积×2÷(上底+下底)求出高,也就是拼成正方形的边长,再根据梯形的面积公式,求原来的梯形面积。
【详解】28×2÷(5+2)
=56÷7
=8(cm)
(8-5+8-2)×8÷2
=72÷2
=36(cm2)
答:原来直角梯形的面积是36平方厘米。
【点睛】本题考查正方形、梯形的面积,解答本题的关键是掌握梯形的面积计算公式。
25.36cm2
【分析】观察图形可知,三角形ABD和三角形AFD是同底同高,所以三角形ABD面积=三角形AFD的面积;根据三角形面积公式:底×高÷2;底是AD=12cm,高是DC=12cm,求出三角形AED的面积,三角形AED的面积=三角形ABD的面积-三角形ABE的面积,再根据三角形面积公式,求出AE的长,进而求出BF的长,三角形BDF的底是BF,高是AF,即可求出三角形BDF的面积。
【详解】根据分析可知:三角形AFD的面积=三角形ABD的面积:
12×12÷2
=144÷2
=72(cm2)
三角形AED 的面积:
72-24=48(cm2)
AE=48×2÷12
=96÷12
=8(cm)
BF=24×2÷8
=48÷8
=6(cm)
三角形BDF的面积:
6×12÷2
=72÷2
=36(cm2)
答:三角形BDF的面积是36cm2。
【点睛】本题考查三角形面积公式的应用,根据同底同高的关系,求出同底同高三角形面积,进而求出需要解答三角形面积。
26.40升
【分析】根据正方体的体积公式:V=a3,长方体的容积(体积)公式:V=abh,用长方体玻璃缸内水的体积加上正方体的铁块的体积减去长方体玻璃缸的容积,即可求出溢出水的体积。
【详解】4×4×4+6×5×3.2-6×5×4
=64+96-120
=160-120
=40(立方分米)
40立方分米=40升
答:缸里的水溢出40升。
【点睛】此题主要考查正方体的体积公式、长方体的容积(体积)公式的灵活运用,关键是熟记公式。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
1.爸爸将净含量为625毫升的一瓶饮料浸没在一个装满水的盆里,盆里溢出的水( )。
A.是625毫升 B.比625毫升多 C.不足625毫升 D.无法确定
2.如图,求CD长度正确的是( )。(单位:dm)
A.5×4÷3 B.3×4÷5 C.5×3÷4 D.5×3×4
3.平行四边形的高有( )条。
A.1 B.2 C.4 D.无数
4.一个长方体中,如果有四个面的面积相等,其余两个面( )。
A.都是长方形 B.都是正方形 C.一个是长方形,一个是正方形 D.不能确定
5.从长7分米、宽6分米、高3分米的长方体中切出一个表面积最大的正方体,该正方体的棱长总和是( )分米。
A.36 B.64 C.72 D.84
6.下图是一个直角三角形和一个正方形组成的梯形,已知直角三角形的面积是15平方厘米,那么梯形的高是( )厘米,面积是( )平方厘米。
A.6;51 B.112;16.5 C.3;33 D.33;51
7.两个( )的梯形可以拼成一个平行四边形。
A.形状相同 B.等底等高 C.完全一样 D.大小相等
8.三角形和平行四边形面积相等,平行四边形的底是三角形底的2倍,若平行四边形的高是4厘米,则三角形的高是( )。
A.2厘米 B.4厘米 C.8厘米 D.16厘米
9.如图,MN是平行四边形DC边上的( ),边DC叫做平行四边形的( )。
10.有两个完全相同的直角三角形,三条边长分别为6cm、8cm和10cm,用它们可以拼出( )种不同的平行四边形,这个三角形斜边上的高是( )cm。
11.一个等腰梯形的周长是40分米,高是5分米,一条腰长8分米,这个等腰梯形的面积是( )平方分米。
12.用一根长72厘米的铁丝做长方体框架,已知长是宽的3倍,宽是高的2倍,这个长方体的体积是( )立方厘米。
13.一个正方体的棱长4分米,它的棱长之和是( )分米,它的表面积为( )平方分米。
14.如图,一个正方体的展开图,2号面相对的是( )号面;4号面相对的是( )号面。
15.单位换算。
0.2m2=( )cm2 ( )dm3( )cm3=6.051dm3
16.在等腰梯形ABCD中,AE⊥BC,BC=2AD,三角形ABE的面积是1cm2,则等腰梯形ABCD的面积是( )cm2。
17.求下图中阴影部分的面积。(单位:分米)
18.求下面各立方体的表面积和体积。(单位:厘米)
19.王大爷有一块三角形的菜园,这个菜园高90米,底80米,王大爷在这块菜地种白菜,如果每平方米可以种2棵白菜,这个菜园一共可以种多少棵白菜?
20.如下图,紧靠小溪有一块梯形苗圃,它的面积是8000平方米。现在要在另外三边围上护栏,为了减少人工测量的工作量,要求只测量一条边就能计算出护栏的长度。
(1)需要测量线段( )的长度。
(2)如果测出这条线段长50米,那么护栏的长度是多少米?
21.外卖给我们的生活带来了很大的便利,这种便利离不开外卖人员的辛苦付出。淘气的叔叔是一个外卖骑手,下图是他的外卖保温包的示意图,做一个这样的保温包至少需要多少平方厘米的材料?(重叠部分忽略不计)
22.一块棱长是80厘米的正方体的铁块,现在要把它溶解成一个横截面积是40平方厘米的长方体,这个长方体的长是多少厘米?请你分析小胖的解题过程的错误点在哪里。并在下面写出正确的解题过程:
23.如图是全运会济南赛区奥体中心游泳馆的主游泳池,它长50米、宽25米、深2米。
(1)建造奥体中心游泳池至少需要挖土多少立方米?
(2)如果要给这个游泳池注1.8米深的水,已知每小时能注水150立方米。需要几小时注完?
24.一个直角梯形,如果把上底延长5cm,下底延长2cm,高不变,面积就增加了28cm2,而且变成一个正方形,求原来直角梯形的面积。
25.如图,在直角梯形ABCD中,AD=DC=12cm,三角形ABE的面积是24cm2,求三角形BDF的面积。
26.一个长方体的玻璃缸,从里面量长,宽,高,水深。如果投入一块棱长为的正方体铁块(如图),缸里的水溢出多少升?
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《专题3 图形与几何- 2025年小升初数学暑假专项提升(沪教版)》参考答案:
1.B
【分析】净含量为625毫升,所以625毫升是瓶子里饮料的体积,那么饮料瓶子的体积必定大于625毫升,由此解答。
【详解】根据分析可知,盆里溢出的水比625毫升多。
故答案为:B
【点睛】本题主要考查学生对体积概念的认识。
2.C
【分析】“平行四边形的面积=底×高”,底和高必须是相对应的,用5×3求出平行四边形的面积,再除以4即可求出其相对应的底CD。
【详解】求CD长度,列式为:5×3÷4;
故答案为:C。
【点睛】熟记平行四边形的面积公式是解答本题的关键。
3.D
【分析】从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。据此可知,平行四边形有两组高,无数条高;据此解答。
【详解】根据平行四边形高的意义可知:平行四边形的高有无数条。
故答案为:D
4.B
【分析】当长方体有相对的两个面是正方形时,其余四个面都是完全一样的长方形,反之,当长方体有4个面的面积相等,其余两个面一定是正方形,由此解决问题。
【详解】当长方体有4个面的面积相等,说明这四个面的长和宽是一样的,一定有四条边相等,即其余两个面是正方形。
故答案选:B
【点睛】此题主要是利用长方体的面的特征:长方体有六个面,每一个面都是长方形(特殊情况有相对的两个面是正方形)来解决问题。
5.A
【分析】从长7分米、宽6分米、高3分米的长方体中切出一个表面积最大的正方体,那么正方体的棱长是长方体的高3分米,根据正方体的棱长总和=棱长×12,代入数据计算即可。
【详解】3<6<7
最大的正方体的棱长是3分米。
正方体的棱长总和:3×12=36(分米)
故答案为:A
【点睛】明确在长方体中切出一个最大的正方体,那么正方体的棱长是长方体最小的棱长。
6.A
【分析】观察图形可知,梯形高等于三角形的高也就是正方形的边长,已知三角形面积和底,根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出三角形的高,进而求出梯形的上底、下底和高的长度,再根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
【详解】梯形的高:15×2÷5
=30÷5
=6(厘米)
梯形面积:(6+6+5)×6÷2
=(12+5)×6÷2
=17×6÷2
=102÷2
=51(平方厘米)
故答案为:A
【点睛】本题也可以利用正方形面积加上三角形面积的和求出梯形面积。
7.C
【分析】根据梯形和平行四边形的关系,直接解题即可。
【详解】两个完全一样的梯形可以拼成一个平行四边形。
故答案为:C
【点睛】本题考查了梯形和平行四边形的关系,明确两个图形的特征是解题的关键。
8.D
【分析】三角形的面积=底×高÷2,平行四边形的面积=底×高,平行四边形的底是三角形底的2倍,则三角形的高是平行四边形的高的4倍,据此解答即可。
【详解】若平行四边形的高是4厘米,则三角形的高是4×4=16厘米。
故答案为:D。
【点睛】本题考查三角形、平行四边形的面积,解答本题的关键是掌握三角形、平行四边形的面积的计算公式。
9. 高 底
【分析】根据平行四边形高的含义:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高;据此解答即可。
【详解】由分析可得:MN是平行四边形DC边上的高,边DC叫做平行四边形的底。
【点睛】此题考查了平行四边形高的含义,应注意灵活运用。
10. 3 4.8
【分析】由于两个完全相同的直角三角形三条边分别是6cm、8cm、10cm,即三条边长度不同,因此可以分别用三条边作公共边来拼,这样可以拼出3种不同的平行四边形;
根据三角形面积公式:面积=底×高÷2,用直角三角形两条直角边做为底和高,求出这个三角形的面积,再利用高=面积×2÷底,即可求出斜边商的高的长度。
【详解】根据分析可知,可以拼出3种不同的平行四边形;
6×8÷2×2÷10
=48÷2×2÷10
=24×2÷10
=48÷10
=4.8(cm)
有两个完全相同的直角三角形,三条边长分别为6cm、8cm和10cm,用它们可以拼出3种不同的平行四边形,这个三角形斜边上的高是4.8cm。
【点睛】本题考察图形的拼组以及三角形面积公式的灵活运用。
11.60
【分析】根据等腰梯形的特征可知,等腰梯形的两条腰相等,用等腰梯形的周长-8×2,求出梯形的上底与下底的和,再根据梯形面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
【详解】(40-8×2)×5÷2
=(40-16)×5÷2
=24×5÷2
=120÷2
=60(平方分米)
一个等腰梯形的周长是40分米,高是5分米,一条腰长8分米,这个等腰梯形的面积是60平方分米。
【点睛】熟练掌握等腰梯形的特征以及梯形面积公式是解答本题的关键。
12.96
【分析】根据题意可知,长是宽的3倍,宽是高的2倍,则可以设高为x厘米,宽为2x厘米,长为(3×2x)厘米,根据长方体棱长和=(长+宽+高)×4,列方程为(3×2x+2x+x)×4=72,然后解出方程,进而求出宽和长,最后根据长方体的体积=长×宽×高,代入数据解答。
【详解】解:设高为x厘米,宽为2x厘米,长为(3×2x)厘米。
(3×2x+2x+x)×4=72
(6x+2x+x)×4=72
9x×4=72
36x=72
36x÷36=72÷36
x=2
宽:2×2=4(厘米)
长:4×3=12(厘米)
12×4×2=96(立方厘米)
这个长方体的体积是96立方厘米。
【点睛】本题主要考查了长方体棱长和公式、长方体体积公式的灵活应用,可列方程解决问题。
13. 48 96
【分析】已知正方体的棱长,求正方体的棱长总和,用公式:正方体的棱长总和=棱长×12,正方体的表面积=棱长×棱长×6,据此列式解答。
【详解】4×12=48(分米)
4×4×6
=16×6
=96(平方分米)
【点睛】此题考查了正方体的棱长总和和表面积的计算,牢记公式认真计算即可。
14. 4 2
【分析】
根据正方体的展开图知识,属于“1-3-2型”,折成正方体后,有公共边的两个面相邻,没有公共边的两个面相对。1号面相对的是5号面;2号面相对的是4号面,3号面相对的是6号面。
【详解】由分析可知:
如图,一个正方体的展开图,2号面相对的是4号面;4号面相对的是2号面。
15. 2000 6 51
【分析】根据1=10000,1=1000,高级单位化低级单位乘进率,低级单位化高级单位除以进率解答。
【详解】0.2×10000=2000(),所以0.2=2000;
因为0.051×1000=51(),所以6.051=651。
16.6
【分析】由S梯形=(上底+下底)×高÷2得,S梯形ABCD=(AD+BC)×AE÷2,因为BC=2AD,所以S梯形ABCD=3AD×AE÷2=1.5AD×AE,据此解答。
【详解】
过A作AF∥CD,交BC于F
由题意可知,AB=CD=AF
则三角形ABF为等腰三角形
S△ABF=2S△ABE=1×2=2(cm2)
S△ABF=BF×AE÷2=2(cm2)
BF×AE=4(cm2)
由图可知,AD=BF=FC
则AD×AE=4(cm2)
S梯形ABCD=1.5×4=6(cm2)
【点睛】作辅助线把三角形ABE的面积转化为梯形ABCD的面积是解答本题的关键。
17.(1)22平方分米;
(2)32平方分米
【分析】(1)将阴影部分两个三角形,其中有一个三角形的底为4分米、高3分米;另一个三角形的底4分米、高(12-4)分米,分别计算面积,再相加即可;
(2)根据等腰直角三角形的特点,分别求出梯形(阴影部分)的上底、下底和高,其中梯形的上底是6,根据直角三角形斜边上的高等于斜边的一半可得,梯形的下底是14与6的和的一半,再用减法得出高,然后根据梯形的面积计算公式求解。
【详解】(1)4×3÷2+4×(12-4)÷2
=6+4×8÷2
=6+16
=22(平方分米)
则阴影部分的面积22平方分米。
(2)(14+6)÷2
=20÷2
=10(分米)
梯形的高:14-10=4(分米)
阴影部分的面积:
(6+10)×4÷2
=16×4÷2
=32(平方分米)
则阴影部分的面积32平方分米。
18.长方体:312平方厘米;360立方厘米。
正方体:150平方厘米;125立方厘米。
【分析】已知题目里的长方体、正方体均为一般情形,故可直接套用公式计算。
S长方体=(长×宽+高×宽+长×高)×2;
V长方体=长×宽×高
S正方体=棱长×棱长×6
V正方体=棱长×棱长×棱长
【详解】(1)(10×6+10×6+6×6)×2
=(60+60+36)×2
=156×2
=312(平方厘米)
10×6×6
=60×6
=360(立方厘米)
(2)5×5×6
=25×6
=150(平方厘米)
5×5×5
=25×5
=125(立方厘米)
19.7200棵
【分析】根据“三角形的面积=底×高÷2”求出这个菜园的面积,一共可以种白菜的棵数=菜园的面积×每平方米可以种白菜的棵数,据此解答。
【详解】90×80÷2×2
=7200÷2×2
=3600×2
=7200(棵)
答:这个菜园一共可以种7200棵白菜。
【点睛】掌握三角形的面积计算公式是解答题目的关键。
20.(1)CD
(2)370米
【分析】(1)由于要计算护栏的长度,相当于:上底(AD线段)+下底(BC线段)+高(CD线段),根据梯形的面积公式:(上底+下底)×高÷2,由于面积已知,如果知道高的长度(即CD线段),那么可以求出上底AD线段加下底BC线段的和,只需要测量一个长度即可,所以测量CD线段的长度。
(2)由于测出这条线段长是50米,也就相当于高是50米,根据梯形的面积公式:面积×2÷高=(上底+下底),把数代入即可求解,之后再把上底和下底还有高这三个线段长度相加即可求出护栏的长度。
【详解】(1)根据梯形面积公式,如果知道梯形的高(CD线段),即可求出上底(AD线段)和下底(BC线段)的和,由此即可知测量CD线段的长。
(2)8000×2÷50
=16000÷50
=320(米)
320+50=370(米)
答:护栏的长共是370米。
【点睛】本题主要考查梯形的面积公式,熟练掌握梯形的面积公式并灵活运用。
21.10138平方厘米
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(50×37+50×37+37×37)×2即可求出做一个这样的保温包至少需要的材料面积。
【详解】(50×37+50×37+37×37)×2
=(1850+1850+1369)×2
=5069×2
=10138(平方厘米)
答:做一个这样的保温包至少需要10138平方厘米的材料。
22.12800厘米;小胖把横截面积看作横截面的周长来计算
【分析】把正方体铁块溶解成一个长方体铁块,体积不变;根据正方体的体积=棱长×棱长×棱长,用80×80×80即可求出铁块的体积,然后根据长方体=横截面积×长,用铁块的体积除以横截面积,即可求出长方体的长;小胖用40÷4,显然是把40的数据当作横截面的周长,然后根据正方形的周长公式求出边长,显然这种算法是错误的。
【详解】80×80×80÷40
=512000÷40
=12800(厘米)
答:这个长方体的长是12800厘米;小胖的解题过程是错的,因为他把横截面积看作横截面的周长来计算。
【点睛】本题主要考查了正方体体积公式和长方体体积公式的灵活应用。
23.(1)2500立方米
(2)15小时
【分析】(1)要求建造奥体中心游泳池至少需要挖土多少立方米,把这个中心游泳池看作一个无盖的长方体,相当于求这个长方体的体积,根据长方体的体积=长×宽×高,代入数值计算即可解答。
(2)根据长方体的体积公式,求出注入的水的总体积,再除以150,所得结果即为需要几小时注完。
【详解】(1)50×25×2=2500(立方米)
答:建造奥体中心游泳池至少需要挖土2500立方米。
(2)50×25×1.8÷150
=2250÷150
=15(小时)
答:需要15小时注完。
24.36cm2
【分析】一个直角梯形,如果把上底延长5cm,下底延长2cm,高不变,面积就增加了28cm2,而且变成一个正方形,说明增加部分是一个上底为2厘米,下底为5厘米,高不变的直角梯形,再根据高=梯形面积×2÷(上底+下底)求出高,也就是拼成正方形的边长,再根据梯形的面积公式,求原来的梯形面积。
【详解】28×2÷(5+2)
=56÷7
=8(cm)
(8-5+8-2)×8÷2
=72÷2
=36(cm2)
答:原来直角梯形的面积是36平方厘米。
【点睛】本题考查正方形、梯形的面积,解答本题的关键是掌握梯形的面积计算公式。
25.36cm2
【分析】观察图形可知,三角形ABD和三角形AFD是同底同高,所以三角形ABD面积=三角形AFD的面积;根据三角形面积公式:底×高÷2;底是AD=12cm,高是DC=12cm,求出三角形AED的面积,三角形AED的面积=三角形ABD的面积-三角形ABE的面积,再根据三角形面积公式,求出AE的长,进而求出BF的长,三角形BDF的底是BF,高是AF,即可求出三角形BDF的面积。
【详解】根据分析可知:三角形AFD的面积=三角形ABD的面积:
12×12÷2
=144÷2
=72(cm2)
三角形AED 的面积:
72-24=48(cm2)
AE=48×2÷12
=96÷12
=8(cm)
BF=24×2÷8
=48÷8
=6(cm)
三角形BDF的面积:
6×12÷2
=72÷2
=36(cm2)
答:三角形BDF的面积是36cm2。
【点睛】本题考查三角形面积公式的应用,根据同底同高的关系,求出同底同高三角形面积,进而求出需要解答三角形面积。
26.40升
【分析】根据正方体的体积公式:V=a3,长方体的容积(体积)公式:V=abh,用长方体玻璃缸内水的体积加上正方体的铁块的体积减去长方体玻璃缸的容积,即可求出溢出水的体积。
【详解】4×4×4+6×5×3.2-6×5×4
=64+96-120
=160-120
=40(立方分米)
40立方分米=40升
答:缸里的水溢出40升。
【点睛】此题主要考查正方体的体积公式、长方体的容积(体积)公式的灵活运用,关键是熟记公式。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
同课章节目录
