专题4统计与可能性-2025年小升初数学暑假专项提升(沪教版)(含解析)
文档属性
| 名称 | 专题4统计与可能性-2025年小升初数学暑假专项提升(沪教版)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 547.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览



文档简介
专题4:统计与可能性
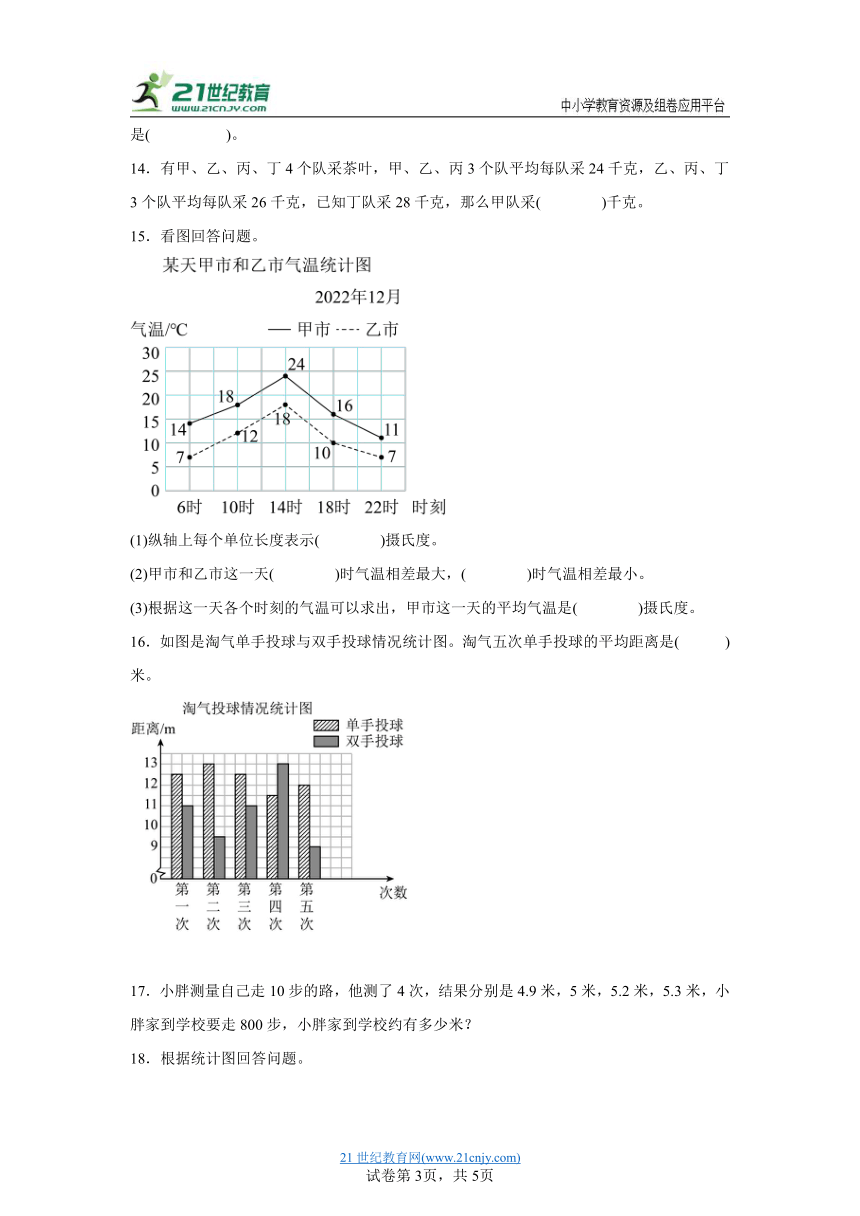
1.五(1)班12月份收集可回收物的情况如下:第一小队有11人,共收集25.3千克;第二小队有9人,平均每人收集2.7千克;第三小队有10人,共收集28.4千克。求五(1)班平均每人收集可回收物多少千克?列式正确的是( )。
A.(25.3+2.7+28.4)÷3 B.25.3÷10+2.7+28.4÷10
C.(25.3÷10+2.7+28.4÷10)÷3 D.(25.3+2.7×9+28.4)÷(11+9+10)
2.图中的虚线表示苹苹本学期已经进行过的体育测试的平均分,灰色直条代表的是期末成绩。下面期末成绩的四种情况中,对平均分影响最大的是( )。
A. B. C. D.
3.人们经常把圆木、钢管、水泥管堆成如下图的样子。下面求总共根数的方法错误的是( )。
A.3+4+5+6+7 B.(3+7)×5÷2 C.5×5 D.(3+7)×5
4.服装商店第一天卖出服装360件,第二天卖出服装450件,第三天上午卖出160件,下午卖出180件,平均每天卖出服装多少件?下面算式中正确的是( )。
A.(360+450+160+180)÷2 B.(360+450+160+180)÷3
C.(360+450+160+180)÷4 D.(360+450+160+180)÷6
5.甲车间3天生产零件90个,乙车间6天生产198个,两个车间平均每天生产几个零件?算式是( )。
A.(90+198)÷2 B.(90+198)÷3 C.(90+198)÷(6+3) D.90÷3+198÷6
6.6月2日,淘气查了所在城市6月3日至5日的天气预报情况如下,下面说法正确的是( )。
A.6月3日有可能会下雨 B.6月4日一定不下雨
C.6月5日一定是晴天 D.以上三种说法都正确
7.盒子里有红、黄、绿三种颜色的小球共20个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
A.5 B.6 C.7 D.8
8.一个盆子里放着2个红球,2个黄球,2个白球和2个蓝球,它们的大小形状相同,从中任意摸出2个球,会出现( )种不同的结果。
A.4 B.8 C.10 D.12
9.有1、2、3、4四张数卡,从中抽取三张,能组成( )个不同的三位数。
10.用“可能”“不可能”或“一定”填空。
(1)某地今天晴天,那么明天 下雨。
(2)8个红球放在口袋里,任意摸一个 是白球。
(3)公鸡 会下蛋。
(4)玻璃杯从很高的地方落在水泥地面上, 会破碎。
(5)有1~6共六个数字的骰子,随便怎么投掷, 出现数字“7”。
(6)每天 有人出生。
11.课外活动时,老师在盒子里装有30个红色棋子,10个黄色棋子。任意摸一个,可能是( )色的,也可能是( )色的,摸到( )色棋子的可能性小一些。
12.下面图形中,一次抽出一张。抽出( )的可能性最大,抽出( )的可能性最小。
13.有四个数,其中每三个数的和分别是45、46、49、52,那么这四个数中最小的一个数是( )。
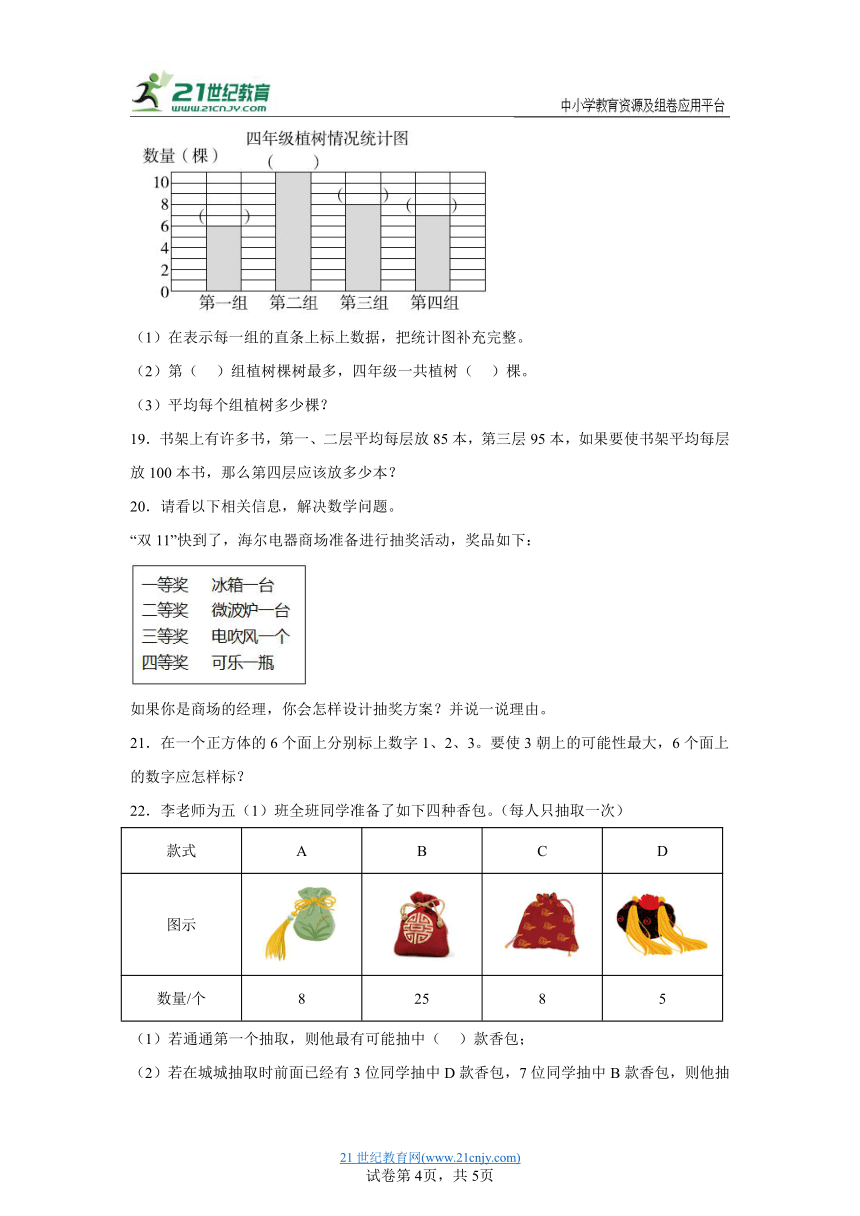
14.有甲、乙、丙、丁4个队采茶叶,甲、乙、丙3个队平均每队采24千克,乙、丙、丁3个队平均每队采26千克,已知丁队采28千克,那么甲队采( )千克。
15.看图回答问题。
(1)纵轴上每个单位长度表示( )摄氏度。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )摄氏度。
16.如图是淘气单手投球与双手投球情况统计图。淘气五次单手投球的平均距离是( )米。
17.小胖测量自己走10步的路,他测了4次,结果分别是4.9米,5米,5.2米,5.3米,小胖家到学校要走800步,小胖家到学校约有多少米?
18.根据统计图回答问题。
(1)在表示每一组的直条上标上数据,把统计图补充完整。
(2)第( )组植树棵树最多,四年级一共植树( )棵。
(3)平均每个组植树多少棵?
19.书架上有许多书,第一、二层平均每层放85本,第三层95本,如果要使书架平均每层放100本书,那么第四层应该放多少本?
20.请看以下相关信息,解决数学问题。
“双11”快到了,海尔电器商场准备进行抽奖活动,奖品如下:
如果你是商场的经理,你会怎样设计抽奖方案?并说一说理由。
21.在一个正方体的6个面上分别标上数字1、2、3。要使3朝上的可能性最大,6个面上的数字应怎样标?
22.李老师为五(1)班全班同学准备了如下四种香包。(每人只抽取一次)
款式 A B C D
图示
数量/个 8 25 8 5
(1)若通通第一个抽取,则他最有可能抽中( )款香包;
(2)若在城城抽取时前面已经有3位同学抽中D款香包,7位同学抽中B款香包,则他抽中哪一款香包的可能性最小?抽中哪两种款式香包的可能性相同?
23.如图,一块梯形木板被分割成黑白两块三角形形状的区域,淘气、笑笑分别向这块平放在水平地上的木板上掷一个骰子,如果这个骰子落在白色区域,淘气赢;如果这个骰子落在黑色区域,笑笑赢。这个游戏公平吗?请说明理由。
24.六(1)班共50人,在记单词竞赛中,成绩按从高到低排列,前30名的平均分比后20名的平均分多12分。李阳把前30名的平均分加上后20名的平均分再除以2,这样得到的结果与全班实际的平均成绩相差多少分?请你想一想,在图上画一画,再试着算一算。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《专题4 统计与可能性- 2025年小升初数学暑假专项提升(沪教版)》参考答案:
1.D
【分析】根据平均数=总数÷份数,先求出收集的总质量,再求出总人数,用总质量÷总人数即可。
【详解】(25.3+2.7×9+28.4)÷(11+9+10)
=(25.3+24.3+28.4)÷(11+9+10)
=78÷30
=2.6(千克)
故答案为:D
【点睛】关键是理解平均数的意义,掌握平均数的求法。
2.D
【分析】平均数能代表一组数据的整体水平,平均数介于一组数据的最大值和最小值之间,平均数容易受一组数据中极端数据的影响,极大或极小的数据都会影响平均数的大小。
【详解】A.期末成绩和苹苹已经进行过的体育测试的平均分相等,不会影响平均分。
B.期末成绩低于苹苹已经进行过的体育测试的平均分,平均分会下降,但是期末成绩和苹苹已经进行过的体育测试的平均分相差不大,对平均分的影响不大。
C.期末成绩高于苹苹已经进行过的体育测试的平均分,平均分会上升,但是期末成绩和苹苹已经进行过的体育测试的平均分相差不大,对平均分的影响不大。
D.期末成绩高于苹苹已经进行过的体育测试的平均分,平均分会上升,期末成绩和苹苹已经进行过的体育测试的平均分相差较大,对平均分的影响较大。
对平均分影响最大的是。
故答案为:D
3.D
【分析】观察图片可知:一共有5层,从最上层到最下层分别是3根、4根、5根、6根、7根,除最上层外,每层都比上一层多1根。据此逐项分析。
【详解】A.3+4+5+6+7,把五层各自的根数相加,可以求出总根数,此选项方法正确;
B.(3+7)×5÷2,把它的截面看作一个上底是3,下底是7,高是5的梯形,根据梯形的面积公式列出算式(3+7)×5÷2,求出梯形的面积即是总根数,此选项方法正确;
C.5×5,从最上层到最下层分别是3根、4根、5根、6根、7根,中间一层的根数是它们的平均数,用平均根数乘层数,即5×5,可以求出总根数,此选项方法正确;
D.(3+7)×5,根据梯形的面积公式,这个式子列式错误,不能求出总根数,此选项方法错误。
故答案为:D
4.B
【分析】根据平均数的意义,把三天的卖出的服装数量相加,再除以3即可求得每天卖出服装多少件。据此解答。
【详解】(360+450+160+180)÷3
=1150÷3
≈383(件)
故答案为:B
【点睛】本题考查了平均数的计算,解答本题的关键是求出第三天一共卖出服装多少件。
5.D
【分析】根据题意,用90÷3,求出甲车间一天平均生产的零件个数;再用198÷6,求出乙车间一天平均生产的零件个数,再把甲车间平均一天生产零件个数+乙车间平均一天生产的零件个数相加,即可解答。
【详解】90÷3+198÷6
=30+33
=63(个)
甲车间3天生产零件90个,乙车间6天生产198个,两个车间平均每天生产几个零件?算式是90÷3+198÷6。
故答案为:D
【点睛】本题主要考查求平均数的计算方法,即生产零件的总个数÷生产零件的天数=平均每天生产零件的个数。
6.A
【分析】天气预报播报的天气只是可能性很大,会出现,并不是一定会出现,据此解答。
【详解】6月3日下雨的可能性大,但也可能不下雨;6月4日可能是多云,但也可能下雨;6月5日晴天的可能性大,但不一定是晴天;所以只有A说法正确。
故答案选:A
【点睛】本题考查不确定事件发生的可能性,应根据可能性的大小,进行分析,进而得出结论。
7.B
【分析】根据各种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【详解】红、黄、绿三种颜色的小球共20个,任意摸一个球,要使摸到红球的可能性最小,则红球的个数<黄球的个数=绿球的个数,根据平均分的定义可知红球不能是7个或7个以上那么最多有6个。
故答案为:B
【点睛】解答此题应结合题意,并考虑可能性的大小,进行分析、解答即可。
8.C
【分析】运用列举法找出可能出现两个球的颜色有多少种情况,即可求解。
【详解】从中任意摸出2个球,可能出现:红、红;红、黄;红、白;红、蓝;黄、黄;黄、白;黄、蓝;白、白;白、蓝;蓝、蓝。
4+3+2+1=10(种)
故答案为:C
【点睛】解决本题的关键是将结果列举出来,再计数。
9.24
【分析】组成的三位数,各个数位的数字是由顺序性的,首先排百位可以是1、2、3、4有4种选法,当百位确定后,然后排十位,有3种选法;最后排个位有2种选法;再根据乘法原理,求出能组成多少个不同的三位数即可。
【详解】4×3×2=24(个)
能组成24个不同的三位数。
【点睛】此题考查排列组合问题,首先考虑排列是否跟顺序有关,再来解答。
10.(1)可能
(2)不可能
(3)不可能
(4)一定
(5)不可能
(6)一定
【分析】“可能”表示不确定事件,“一定”表示确定事件中的必然事件,“不可能”属于确定事件中的不可能事件,结合实际生活,按要求写出即可。
【详解】(1)某地今天晴天,那么明天可能下雨。
(2)8个红球放在口袋里,任意摸一个不可能是白球。
(3)公鸡不可能会下蛋。
(4)玻璃杯从很高的地方落在水泥地面上,一定会破碎。
(5)有1~6共六个数字的骰子,随便怎么投掷,不可能出现数字“7”。
(6)每天一定有人出生。
【点睛】此题考查了事件的确定性和不确定性;解答此题的关键是先确定该事件是随机事件、必然事件还是不可能事件,然后进行分析,得出答案。
11. 红 黄 黄
【分析】根据题意,盒子里有30个红色棋子,10个黄色棋子,那么任意摸一个,就有可能摸到这两种颜色棋子中的任何一个,所以有两种可能的结果。
根据可能性大小的判断方法,比较盒子里红色棋子、黄色棋子的数量多少,数量少的,摸到的可能性就小。
【详解】10<30,黄色棋子数量少。
课外活动时,老师在盒子里装有30个红色棋子,10个黄色棋子。任意摸一个,可能是(红)色的,也可能是(黄)色的,摸到(黄)色棋子的可能性小一些。
12.
【分析】分析题目,哪种图形的卡片多,则随机抽出一张,抽出哪种图形的卡片就多,哪种图形的卡片少,则抽出哪种图形的卡片就少,据此解答。
【详解】
有5张,3张,2张。
5>3>2
一次抽出一张。抽出的可能性最大,抽出的可能性最小。
13.12
【分析】已知有四个数,设为a、b、c、d 。每三个数求和,会得到a+b+c、a+b+d、a+c+d、b+c+d这4个和,对应题目中的45、46、49、52 。
把这4个和相加,即(a+b+c)+(a+b+d)+(a+c+d)+(b+c+d),整理后是3(a+b+c+d) ,这说明4个和的总和是四个数总和的3倍。
所以先将4个和相加,再除以3,就能求出四个数的总和a+b+c+d 。
要找最小的数,因为最大的“三个数的和”(52 )是除最小数外其他三个数的和,所以用四个数的总和减去最大的三个数的和,结果就是最小数。
【详解】(45+46+49+52)÷3
=192÷3
=64
64-52=12
那么这四个数中最小的一个数是12。
【点睛】解题关键在于两点:一是发现 “四组每三个数的和相加,等于四个数总和的3倍”,以此求出四个数的总和;二是明确 “最大的三个数的和,对应的是除最小数外另外三个数的和”,用总和减去这个最大和,就能精准得到最小数,这两步逻辑紧密关联,是突破本题的核心思路。
14.22
【分析】由题意得,甲、乙、丙3个队平均每队采24千克,那么直接用24乘3可以算出甲、乙、丙3个队一共采茶多少千克。乙、丙、丁3个队平均每队采26千克,直接用26乘3即可算出乙、丙、丁3个队一共采茶多少千克。已知丁队采28千克,那么用乙、丙、丁3个队一共采茶的数量减去28可以算出乙、丙2个队一共采茶的数量。最后再用甲、乙、丙3个队一共采茶的数量减去乙、丙2个队一共采茶的数量,即可算出甲队采茶多少千克。
【详解】24×3=72(千克)
26×3=78(千克)
78-28=50(千克)
72-50=22(千克)
故甲队采茶22千克。
15.(1)5
(2) 6 22
(3)16.6
【分析】(1)纵轴表示气温,观察纵轴即可确定每个单位长度表示的温度;
(2)分别计算每个时刻的气温差,比较即可;
(3)根据平均数=总数量÷总份数,列式计算即可。
【详解】(1)纵轴上每个单位长度表示5摄氏度。
(2)14-7=7(摄氏度)、18-12=6(摄氏度)、24-18=6(摄氏度)、
16-10=6(摄氏度)、11-7=4(摄氏度)
7>6>4
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(摄氏度)
甲市这一天的平均气温是16.6摄氏度。
16.12.3
【分析】从统计图中可知,5次单手投球的米数分别是:12.5、13、12.5、11.5、12,即五次单手投球的平均距离=5次的总和÷次数。
【详解】(12.5+13+12.5+11.5+12)÷5
=61.5÷5
=12.3(米)
则淘气五次单手投球的平均距离是12.3米。
17.408米
【分析】4次的结果分别为4.9米,5米,5.2米,5.3米,则将4.9米,5米,5.2米,5.3米这四个数相加再除以4,即可计算出平均10步能走多少米,再除以10计算出平均每步多少米。小胖家到学校要走800步,用800乘平均每步走的米数,即可计算出小胖家到学校多少米。
【详解】(4.9+5+5.2+5.3)÷4÷10
=(9.9+5.2+5.3)÷4÷10
=(15.1+5.3)÷4÷10
=20.4÷4÷10
=5.1÷10
=0.51(米)
0.51×800=408(米)
答:小胖家到学校约有408米。
18.(1)见详解
(2)二;32
(3)8棵
【分析】(1)根据条形统计图可知,2格表示2棵,则每格表示1棵。先数出各个直条中有几格,就表示几棵树。
(2)比较各个组植树棵数大小。将各个组植树棵数相加,求出四年级植树总棵数。
(3)用四年级植树总棵数除以4,求出平均每组植树棵数。
【详解】
(1)
(2)11>8>7>6
6+11+8+7=32(棵)
第二组植树棵树最多,四年级一共植树32棵。
(3)32÷4=8(棵)
答:平均每个组植树8棵。
【点睛】此题考查的目的是理解掌握统计图的特点及作用、平均数的意义和求法,能够根据统计图提供的信息,解决有关的实际问题。
19.135本
【解析】略
20.如果我是经理我会这样设计:一等奖商品最贵,数量最少;二等奖数量次之,三等奖数量第三少,四等奖数量最多;因为贵的商品越少,商场的利益越大。(答案不唯一)
【分析】商场的经理为保证商场利益,应该把最贵的一等奖数量设置最少,摸到的可能性最小;二等奖第二少,三等奖第三少,四等奖最多,据此解答即可(答案不唯一)。
【详解】答:如果我是经理我会这样设计:一等奖商品最贵,数量最少;二等奖数量次之,三等奖数量第三少,四等奖数量最多;因为贵的商品越少,商场的利益越大。(答案不唯一)
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的概念。
21.要使3朝上的可能性最大,一个面标1,一个面标2,剩下的4个面标3。
【分析】一个正方体有6个面,可标上数字1、2、3,要想掷一次后出现3的可能性大,只要尽可能多标3即可。
【详解】一个正方体有6个面,一个面标1,一个面标2,剩下的4个面标3,这样掷一次后出现3的可能性最大。
答:要使3朝上的可能性最大,一个面标1,一个面标2,剩下的4个面标3。
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的大小由数量多少决定。
22.(1)B
(2)D款;A款和C款
【分析】(1)可能性大小的判断,从香包的数量上分析。数量最多的,抽到的可能性最大,数量最少的,抽到的可能性最小,数量相等的,抽到的可能性一样。据此解答。
(2)在城城抽取时,A款有8个,B款有25-7=18个,C款有8个,D款有5-3=2个。据此即可判断。
【详解】(1)25>8=8>5
若通通第一个抽取,则他最有可能抽中B款香包;
(2)25-7=18(个)
5-3=2(个)
18>8=8>2
答:他抽中D款香包的可能性最小;抽中A款和C款香包的可能性相同。
23.不公平;理由见详解
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
据此根据梯形的特征和三角形面积公式,比较两个三角形的面积,面积相等,游戏公平;面积不相等,则游戏不公平,据此解答。
【详解】白三角形的底等于梯形的上底,高等于梯形的高;
黑三角形的底等于梯形的下底,高等于梯形的高;
白三角形的底<黑三角形的底,则白三角形的面积<黑三角形的面积,淘气赢的机会少,笑笑赢的机会大,游戏不公平。
24.图见详解;1.2分
【分析】先画一个长方形表示前30人的总分,长为平均分,宽为人数;再画第二个长方形表示后20人的总分,两部分的长的差为12;从表示前30人的长方形中移出一部分来填补表示后20人的长方形可知,李阳把前30名的平均分加上后20名的平均分再除以2,李阳少算了(6×10=60分),这样得到的结果与全班实际的平均成绩相差(60÷50=1.2)分;据此解答。
【详解】如图所示:
李阳少算了:6×10=60(分)
李阳少算的平均分:60÷(20+30)
=60÷50
=1.2(分)
答:李阳这样得到的结果与全班实际的平均成绩相差1.2分。
【点睛】本题需要学生正确理解平均分的意义和求法,关键是明确李阳少算了60分。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
1.五(1)班12月份收集可回收物的情况如下:第一小队有11人,共收集25.3千克;第二小队有9人,平均每人收集2.7千克;第三小队有10人,共收集28.4千克。求五(1)班平均每人收集可回收物多少千克?列式正确的是( )。
A.(25.3+2.7+28.4)÷3 B.25.3÷10+2.7+28.4÷10
C.(25.3÷10+2.7+28.4÷10)÷3 D.(25.3+2.7×9+28.4)÷(11+9+10)
2.图中的虚线表示苹苹本学期已经进行过的体育测试的平均分,灰色直条代表的是期末成绩。下面期末成绩的四种情况中,对平均分影响最大的是( )。
A. B. C. D.
3.人们经常把圆木、钢管、水泥管堆成如下图的样子。下面求总共根数的方法错误的是( )。
A.3+4+5+6+7 B.(3+7)×5÷2 C.5×5 D.(3+7)×5
4.服装商店第一天卖出服装360件,第二天卖出服装450件,第三天上午卖出160件,下午卖出180件,平均每天卖出服装多少件?下面算式中正确的是( )。
A.(360+450+160+180)÷2 B.(360+450+160+180)÷3
C.(360+450+160+180)÷4 D.(360+450+160+180)÷6
5.甲车间3天生产零件90个,乙车间6天生产198个,两个车间平均每天生产几个零件?算式是( )。
A.(90+198)÷2 B.(90+198)÷3 C.(90+198)÷(6+3) D.90÷3+198÷6
6.6月2日,淘气查了所在城市6月3日至5日的天气预报情况如下,下面说法正确的是( )。
A.6月3日有可能会下雨 B.6月4日一定不下雨
C.6月5日一定是晴天 D.以上三种说法都正确
7.盒子里有红、黄、绿三种颜色的小球共20个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
A.5 B.6 C.7 D.8
8.一个盆子里放着2个红球,2个黄球,2个白球和2个蓝球,它们的大小形状相同,从中任意摸出2个球,会出现( )种不同的结果。
A.4 B.8 C.10 D.12
9.有1、2、3、4四张数卡,从中抽取三张,能组成( )个不同的三位数。
10.用“可能”“不可能”或“一定”填空。
(1)某地今天晴天,那么明天 下雨。
(2)8个红球放在口袋里,任意摸一个 是白球。
(3)公鸡 会下蛋。
(4)玻璃杯从很高的地方落在水泥地面上, 会破碎。
(5)有1~6共六个数字的骰子,随便怎么投掷, 出现数字“7”。
(6)每天 有人出生。
11.课外活动时,老师在盒子里装有30个红色棋子,10个黄色棋子。任意摸一个,可能是( )色的,也可能是( )色的,摸到( )色棋子的可能性小一些。
12.下面图形中,一次抽出一张。抽出( )的可能性最大,抽出( )的可能性最小。
13.有四个数,其中每三个数的和分别是45、46、49、52,那么这四个数中最小的一个数是( )。
14.有甲、乙、丙、丁4个队采茶叶,甲、乙、丙3个队平均每队采24千克,乙、丙、丁3个队平均每队采26千克,已知丁队采28千克,那么甲队采( )千克。
15.看图回答问题。
(1)纵轴上每个单位长度表示( )摄氏度。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )摄氏度。
16.如图是淘气单手投球与双手投球情况统计图。淘气五次单手投球的平均距离是( )米。
17.小胖测量自己走10步的路,他测了4次,结果分别是4.9米,5米,5.2米,5.3米,小胖家到学校要走800步,小胖家到学校约有多少米?
18.根据统计图回答问题。
(1)在表示每一组的直条上标上数据,把统计图补充完整。
(2)第( )组植树棵树最多,四年级一共植树( )棵。
(3)平均每个组植树多少棵?
19.书架上有许多书,第一、二层平均每层放85本,第三层95本,如果要使书架平均每层放100本书,那么第四层应该放多少本?
20.请看以下相关信息,解决数学问题。
“双11”快到了,海尔电器商场准备进行抽奖活动,奖品如下:
如果你是商场的经理,你会怎样设计抽奖方案?并说一说理由。
21.在一个正方体的6个面上分别标上数字1、2、3。要使3朝上的可能性最大,6个面上的数字应怎样标?
22.李老师为五(1)班全班同学准备了如下四种香包。(每人只抽取一次)
款式 A B C D
图示
数量/个 8 25 8 5
(1)若通通第一个抽取,则他最有可能抽中( )款香包;
(2)若在城城抽取时前面已经有3位同学抽中D款香包,7位同学抽中B款香包,则他抽中哪一款香包的可能性最小?抽中哪两种款式香包的可能性相同?
23.如图,一块梯形木板被分割成黑白两块三角形形状的区域,淘气、笑笑分别向这块平放在水平地上的木板上掷一个骰子,如果这个骰子落在白色区域,淘气赢;如果这个骰子落在黑色区域,笑笑赢。这个游戏公平吗?请说明理由。
24.六(1)班共50人,在记单词竞赛中,成绩按从高到低排列,前30名的平均分比后20名的平均分多12分。李阳把前30名的平均分加上后20名的平均分再除以2,这样得到的结果与全班实际的平均成绩相差多少分?请你想一想,在图上画一画,再试着算一算。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《专题4 统计与可能性- 2025年小升初数学暑假专项提升(沪教版)》参考答案:
1.D
【分析】根据平均数=总数÷份数,先求出收集的总质量,再求出总人数,用总质量÷总人数即可。
【详解】(25.3+2.7×9+28.4)÷(11+9+10)
=(25.3+24.3+28.4)÷(11+9+10)
=78÷30
=2.6(千克)
故答案为:D
【点睛】关键是理解平均数的意义,掌握平均数的求法。
2.D
【分析】平均数能代表一组数据的整体水平,平均数介于一组数据的最大值和最小值之间,平均数容易受一组数据中极端数据的影响,极大或极小的数据都会影响平均数的大小。
【详解】A.期末成绩和苹苹已经进行过的体育测试的平均分相等,不会影响平均分。
B.期末成绩低于苹苹已经进行过的体育测试的平均分,平均分会下降,但是期末成绩和苹苹已经进行过的体育测试的平均分相差不大,对平均分的影响不大。
C.期末成绩高于苹苹已经进行过的体育测试的平均分,平均分会上升,但是期末成绩和苹苹已经进行过的体育测试的平均分相差不大,对平均分的影响不大。
D.期末成绩高于苹苹已经进行过的体育测试的平均分,平均分会上升,期末成绩和苹苹已经进行过的体育测试的平均分相差较大,对平均分的影响较大。
对平均分影响最大的是。
故答案为:D
3.D
【分析】观察图片可知:一共有5层,从最上层到最下层分别是3根、4根、5根、6根、7根,除最上层外,每层都比上一层多1根。据此逐项分析。
【详解】A.3+4+5+6+7,把五层各自的根数相加,可以求出总根数,此选项方法正确;
B.(3+7)×5÷2,把它的截面看作一个上底是3,下底是7,高是5的梯形,根据梯形的面积公式列出算式(3+7)×5÷2,求出梯形的面积即是总根数,此选项方法正确;
C.5×5,从最上层到最下层分别是3根、4根、5根、6根、7根,中间一层的根数是它们的平均数,用平均根数乘层数,即5×5,可以求出总根数,此选项方法正确;
D.(3+7)×5,根据梯形的面积公式,这个式子列式错误,不能求出总根数,此选项方法错误。
故答案为:D
4.B
【分析】根据平均数的意义,把三天的卖出的服装数量相加,再除以3即可求得每天卖出服装多少件。据此解答。
【详解】(360+450+160+180)÷3
=1150÷3
≈383(件)
故答案为:B
【点睛】本题考查了平均数的计算,解答本题的关键是求出第三天一共卖出服装多少件。
5.D
【分析】根据题意,用90÷3,求出甲车间一天平均生产的零件个数;再用198÷6,求出乙车间一天平均生产的零件个数,再把甲车间平均一天生产零件个数+乙车间平均一天生产的零件个数相加,即可解答。
【详解】90÷3+198÷6
=30+33
=63(个)
甲车间3天生产零件90个,乙车间6天生产198个,两个车间平均每天生产几个零件?算式是90÷3+198÷6。
故答案为:D
【点睛】本题主要考查求平均数的计算方法,即生产零件的总个数÷生产零件的天数=平均每天生产零件的个数。
6.A
【分析】天气预报播报的天气只是可能性很大,会出现,并不是一定会出现,据此解答。
【详解】6月3日下雨的可能性大,但也可能不下雨;6月4日可能是多云,但也可能下雨;6月5日晴天的可能性大,但不一定是晴天;所以只有A说法正确。
故答案选:A
【点睛】本题考查不确定事件发生的可能性,应根据可能性的大小,进行分析,进而得出结论。
7.B
【分析】根据各种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【详解】红、黄、绿三种颜色的小球共20个,任意摸一个球,要使摸到红球的可能性最小,则红球的个数<黄球的个数=绿球的个数,根据平均分的定义可知红球不能是7个或7个以上那么最多有6个。
故答案为:B
【点睛】解答此题应结合题意,并考虑可能性的大小,进行分析、解答即可。
8.C
【分析】运用列举法找出可能出现两个球的颜色有多少种情况,即可求解。
【详解】从中任意摸出2个球,可能出现:红、红;红、黄;红、白;红、蓝;黄、黄;黄、白;黄、蓝;白、白;白、蓝;蓝、蓝。
4+3+2+1=10(种)
故答案为:C
【点睛】解决本题的关键是将结果列举出来,再计数。
9.24
【分析】组成的三位数,各个数位的数字是由顺序性的,首先排百位可以是1、2、3、4有4种选法,当百位确定后,然后排十位,有3种选法;最后排个位有2种选法;再根据乘法原理,求出能组成多少个不同的三位数即可。
【详解】4×3×2=24(个)
能组成24个不同的三位数。
【点睛】此题考查排列组合问题,首先考虑排列是否跟顺序有关,再来解答。
10.(1)可能
(2)不可能
(3)不可能
(4)一定
(5)不可能
(6)一定
【分析】“可能”表示不确定事件,“一定”表示确定事件中的必然事件,“不可能”属于确定事件中的不可能事件,结合实际生活,按要求写出即可。
【详解】(1)某地今天晴天,那么明天可能下雨。
(2)8个红球放在口袋里,任意摸一个不可能是白球。
(3)公鸡不可能会下蛋。
(4)玻璃杯从很高的地方落在水泥地面上,一定会破碎。
(5)有1~6共六个数字的骰子,随便怎么投掷,不可能出现数字“7”。
(6)每天一定有人出生。
【点睛】此题考查了事件的确定性和不确定性;解答此题的关键是先确定该事件是随机事件、必然事件还是不可能事件,然后进行分析,得出答案。
11. 红 黄 黄
【分析】根据题意,盒子里有30个红色棋子,10个黄色棋子,那么任意摸一个,就有可能摸到这两种颜色棋子中的任何一个,所以有两种可能的结果。
根据可能性大小的判断方法,比较盒子里红色棋子、黄色棋子的数量多少,数量少的,摸到的可能性就小。
【详解】10<30,黄色棋子数量少。
课外活动时,老师在盒子里装有30个红色棋子,10个黄色棋子。任意摸一个,可能是(红)色的,也可能是(黄)色的,摸到(黄)色棋子的可能性小一些。
12.
【分析】分析题目,哪种图形的卡片多,则随机抽出一张,抽出哪种图形的卡片就多,哪种图形的卡片少,则抽出哪种图形的卡片就少,据此解答。
【详解】
有5张,3张,2张。
5>3>2
一次抽出一张。抽出的可能性最大,抽出的可能性最小。
13.12
【分析】已知有四个数,设为a、b、c、d 。每三个数求和,会得到a+b+c、a+b+d、a+c+d、b+c+d这4个和,对应题目中的45、46、49、52 。
把这4个和相加,即(a+b+c)+(a+b+d)+(a+c+d)+(b+c+d),整理后是3(a+b+c+d) ,这说明4个和的总和是四个数总和的3倍。
所以先将4个和相加,再除以3,就能求出四个数的总和a+b+c+d 。
要找最小的数,因为最大的“三个数的和”(52 )是除最小数外其他三个数的和,所以用四个数的总和减去最大的三个数的和,结果就是最小数。
【详解】(45+46+49+52)÷3
=192÷3
=64
64-52=12
那么这四个数中最小的一个数是12。
【点睛】解题关键在于两点:一是发现 “四组每三个数的和相加,等于四个数总和的3倍”,以此求出四个数的总和;二是明确 “最大的三个数的和,对应的是除最小数外另外三个数的和”,用总和减去这个最大和,就能精准得到最小数,这两步逻辑紧密关联,是突破本题的核心思路。
14.22
【分析】由题意得,甲、乙、丙3个队平均每队采24千克,那么直接用24乘3可以算出甲、乙、丙3个队一共采茶多少千克。乙、丙、丁3个队平均每队采26千克,直接用26乘3即可算出乙、丙、丁3个队一共采茶多少千克。已知丁队采28千克,那么用乙、丙、丁3个队一共采茶的数量减去28可以算出乙、丙2个队一共采茶的数量。最后再用甲、乙、丙3个队一共采茶的数量减去乙、丙2个队一共采茶的数量,即可算出甲队采茶多少千克。
【详解】24×3=72(千克)
26×3=78(千克)
78-28=50(千克)
72-50=22(千克)
故甲队采茶22千克。
15.(1)5
(2) 6 22
(3)16.6
【分析】(1)纵轴表示气温,观察纵轴即可确定每个单位长度表示的温度;
(2)分别计算每个时刻的气温差,比较即可;
(3)根据平均数=总数量÷总份数,列式计算即可。
【详解】(1)纵轴上每个单位长度表示5摄氏度。
(2)14-7=7(摄氏度)、18-12=6(摄氏度)、24-18=6(摄氏度)、
16-10=6(摄氏度)、11-7=4(摄氏度)
7>6>4
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(摄氏度)
甲市这一天的平均气温是16.6摄氏度。
16.12.3
【分析】从统计图中可知,5次单手投球的米数分别是:12.5、13、12.5、11.5、12,即五次单手投球的平均距离=5次的总和÷次数。
【详解】(12.5+13+12.5+11.5+12)÷5
=61.5÷5
=12.3(米)
则淘气五次单手投球的平均距离是12.3米。
17.408米
【分析】4次的结果分别为4.9米,5米,5.2米,5.3米,则将4.9米,5米,5.2米,5.3米这四个数相加再除以4,即可计算出平均10步能走多少米,再除以10计算出平均每步多少米。小胖家到学校要走800步,用800乘平均每步走的米数,即可计算出小胖家到学校多少米。
【详解】(4.9+5+5.2+5.3)÷4÷10
=(9.9+5.2+5.3)÷4÷10
=(15.1+5.3)÷4÷10
=20.4÷4÷10
=5.1÷10
=0.51(米)
0.51×800=408(米)
答:小胖家到学校约有408米。
18.(1)见详解
(2)二;32
(3)8棵
【分析】(1)根据条形统计图可知,2格表示2棵,则每格表示1棵。先数出各个直条中有几格,就表示几棵树。
(2)比较各个组植树棵数大小。将各个组植树棵数相加,求出四年级植树总棵数。
(3)用四年级植树总棵数除以4,求出平均每组植树棵数。
【详解】
(1)
(2)11>8>7>6
6+11+8+7=32(棵)
第二组植树棵树最多,四年级一共植树32棵。
(3)32÷4=8(棵)
答:平均每个组植树8棵。
【点睛】此题考查的目的是理解掌握统计图的特点及作用、平均数的意义和求法,能够根据统计图提供的信息,解决有关的实际问题。
19.135本
【解析】略
20.如果我是经理我会这样设计:一等奖商品最贵,数量最少;二等奖数量次之,三等奖数量第三少,四等奖数量最多;因为贵的商品越少,商场的利益越大。(答案不唯一)
【分析】商场的经理为保证商场利益,应该把最贵的一等奖数量设置最少,摸到的可能性最小;二等奖第二少,三等奖第三少,四等奖最多,据此解答即可(答案不唯一)。
【详解】答:如果我是经理我会这样设计:一等奖商品最贵,数量最少;二等奖数量次之,三等奖数量第三少,四等奖数量最多;因为贵的商品越少,商场的利益越大。(答案不唯一)
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的概念。
21.要使3朝上的可能性最大,一个面标1,一个面标2,剩下的4个面标3。
【分析】一个正方体有6个面,可标上数字1、2、3,要想掷一次后出现3的可能性大,只要尽可能多标3即可。
【详解】一个正方体有6个面,一个面标1,一个面标2,剩下的4个面标3,这样掷一次后出现3的可能性最大。
答:要使3朝上的可能性最大,一个面标1,一个面标2,剩下的4个面标3。
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的大小由数量多少决定。
22.(1)B
(2)D款;A款和C款
【分析】(1)可能性大小的判断,从香包的数量上分析。数量最多的,抽到的可能性最大,数量最少的,抽到的可能性最小,数量相等的,抽到的可能性一样。据此解答。
(2)在城城抽取时,A款有8个,B款有25-7=18个,C款有8个,D款有5-3=2个。据此即可判断。
【详解】(1)25>8=8>5
若通通第一个抽取,则他最有可能抽中B款香包;
(2)25-7=18(个)
5-3=2(个)
18>8=8>2
答:他抽中D款香包的可能性最小;抽中A款和C款香包的可能性相同。
23.不公平;理由见详解
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
据此根据梯形的特征和三角形面积公式,比较两个三角形的面积,面积相等,游戏公平;面积不相等,则游戏不公平,据此解答。
【详解】白三角形的底等于梯形的上底,高等于梯形的高;
黑三角形的底等于梯形的下底,高等于梯形的高;
白三角形的底<黑三角形的底,则白三角形的面积<黑三角形的面积,淘气赢的机会少,笑笑赢的机会大,游戏不公平。
24.图见详解;1.2分
【分析】先画一个长方形表示前30人的总分,长为平均分,宽为人数;再画第二个长方形表示后20人的总分,两部分的长的差为12;从表示前30人的长方形中移出一部分来填补表示后20人的长方形可知,李阳把前30名的平均分加上后20名的平均分再除以2,李阳少算了(6×10=60分),这样得到的结果与全班实际的平均成绩相差(60÷50=1.2)分;据此解答。
【详解】如图所示:
李阳少算了:6×10=60(分)
李阳少算的平均分:60÷(20+30)
=60÷50
=1.2(分)
答:李阳这样得到的结果与全班实际的平均成绩相差1.2分。
【点睛】本题需要学生正确理解平均分的意义和求法,关键是明确李阳少算了60分。
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
同课章节目录
