2025年内蒙古自治区中考数学真题试卷(含答案)
文档属性
| 名称 | 2025年内蒙古自治区中考数学真题试卷(含答案) | 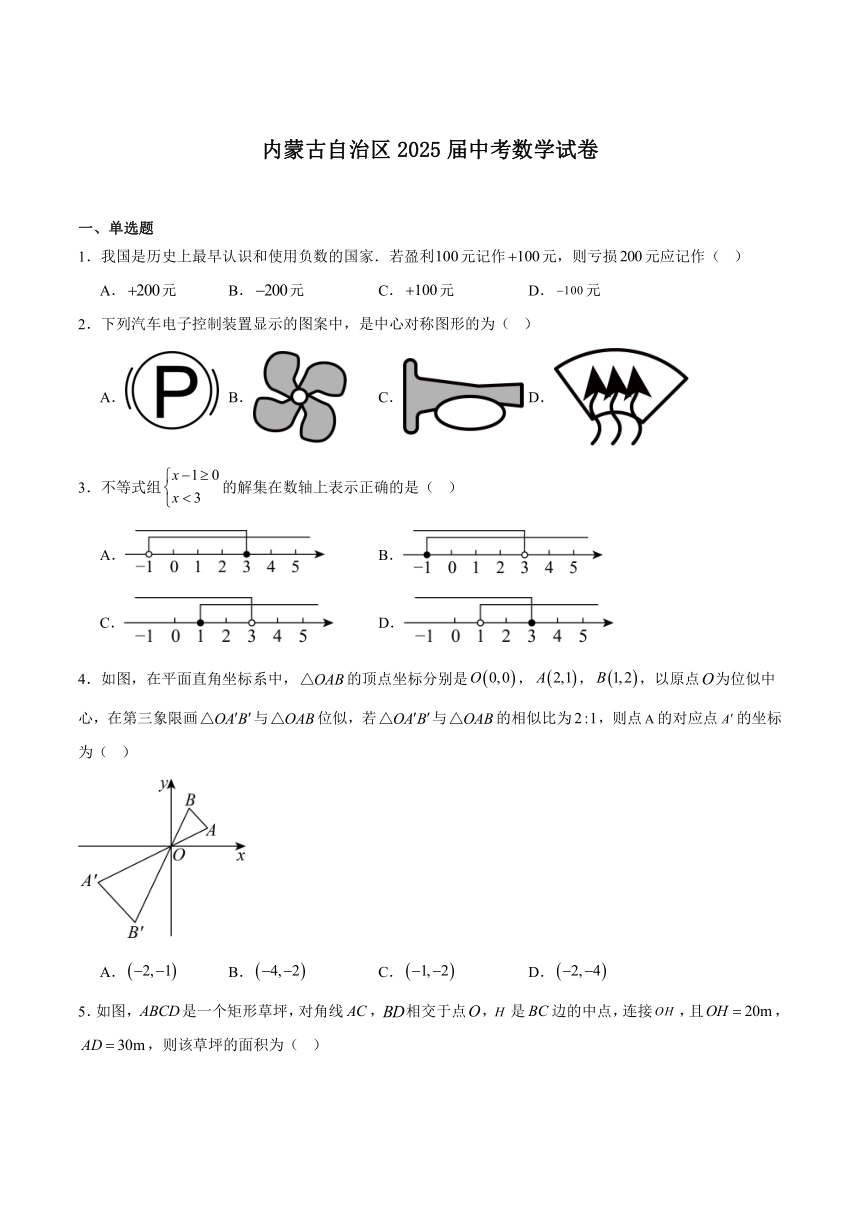 | |
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 16:32:18 | ||
图片预览





文档简介
内蒙古自治区2025届中考数学试卷
一、单选题
1.我国是历史上最早认识和使用负数的国家.若盈利元记作元,则亏损元应记作( )
A.元 B.元 C.元 D.元
2.下列汽车电子控制装置显示的图案中,是中心对称图形的为( )
A. B. C. D.
3.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,的顶点坐标分别是,,,以原点为位似中心,在第三象限画与位似,若与的相似比为,则点的对应点的坐标为( )
A. B. C. D.
5.如图,是一个矩形草坪,对角线,相交于点,是边的中点,连接,且,,则该草坪的面积为( )
A. B. C. D.
6.如图,直线,点,分别在直线,上,连接,以点为圆心,适当长为半径画弧.交射线于点,交于点,再分别以点,为圆心,大于的长为半径画弧(两弧半径相等),两弧在的内部相交于点,画射线交于点,若,则的度数为( )
A. B. C. D.
7.在闭合电路中,通过定值电阻的电流(单位:A)是它两端的电压(单位:)的正比例函数,其图象如图所示,当该电阻两端的电压为时,通过它的电流为( )
A. B. C. D.
8.已知点,都在反比例函数的图象上,则下列结论一定正确的是( )
A. B.
C.当时, D.当时,
二、填空题
9.在单词(班级)中随机选择一个字母,则选中字母“”的概率是 .
10.冰糖葫芦是我国传统小吃,若大串冰糖葫芦每根穿5个山楂,小串冰糖葫芦每根穿3个山楂,则穿根大串和根小串冰糖葫芦需要的山楂总个数用代数式表示为 .
11.如图,因地形原因,湖泊两端,的距离不易测量,某科技小组需要用无人机进行测量.他们将无人机上升并飞行至距湖面的点处.从点测得点的俯角为,测得点的俯角为(,,三点在同一竖直平面内),则湖泊两端,的距离为 (结果保留根号).
12.如图,在菱形中,,对角线的长为,是的中点,是上一点,连接.若,则的长为 .
三、解答题
13.计算:
(1);
(2).
14.每年的6月6日是全国爱眼日,某校为了解八年级学生的视力健康状况,从该年级学生今年的体检结果中随机抽取了40名学生的视力数据,将所得视力数据进行整理后分为5组,得到如下的频数分布表:
分组 A B C D E
人数(频数) 2 8 14 12 4
请根据所给信息,解答下列问题:
(1)这40名学生视力的中位数落在哪个组内
(2)该校八年级共有500名学生.
①根据上表数据,请估计这500名八年级学生的视力在范围内的人数;
②从去年同期这500名学生的体检结果中可知,视力在范围内的人数为263人.如果你是该校的一名学生,请说明这500名学生今年和去年视力在范围内的人数变化情况,并为学校提一条保护学生视力的合理化建议.
15.智能机器人的广泛应用是智慧农业的发展趋势之一.某品牌苹果采摘机器人的机械手能自动对成熟的苹果进行采摘,一个机器人可以搭载多个机械手同时工作.在正常工作状态下,该机器人的每一个机械手平均秒采摘一个成熟的苹果,它的一个机械手用800秒采摘苹果的个数比用600秒采摘苹果的个数多25个.
(1)求的值;
(2)现需要一定数量的苹果发往外地,采摘工作由多个机器人共同完成.每个机器人搭载4个相同的机械手,那么至少需要多少个这样的机器人同时工作1小时,才能使采摘的苹果个数不少于10000个
16.如图,是的直径,半径,垂足为,,是延长线上一点,连接,交于点,连接,.过点作的切线,切点为,交的延长线于点.
(1)求的长;
(2)求的度数;
(3)求的值.
17.问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
18.如图,是一个平行四边形纸片,是一条对角线,,.
(1)如图1,将平行四边形纸片沿折叠,点的对应点落在点处,交于点.
①试猜想与的数量关系,并说明理由;
②求的面积;
(2)如图2,点,分别在平行四边形纸片的,边上,连接,且,将平行四边形纸片沿折叠,使点的对应点落在边上,求的长.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B B C B C D A D
9.
10./
11.
12.
13.(1)
(2)
(1)解:
;
(2)解:
.
14.(1)组
(2)①200人;②合理即可
(1)解:∵随机抽取了40名学生,
∴中位数为第名学生的视力的平均数,
由频数分布表可得第名学生在组,
∴这40名学生视力的中位数落在组;
(2)解:①由题意得,(人)
答:500名八年级学生的视力在范围内有200人;
②因为,
所以今年学生视力在范围内的人数相比去年减少,
建议:①读书时,坐姿要端正,不要在光线不好的地方看书;②保证充足的睡眠,饮食均衡;③减少电子产品的使用(合理即可).
15.(1)8
(2)至少需要6个这样的机器人
(1)解:由题意得,,
解得:,
经检验:是原方程的解,且符合题意,
∴的值为8;
(2)解:1小时,
设需要个这样的机器人,
由题意得:,
解得:,
∵为正整数,
∴最小值为6,
答:至少需要6个这样的机器人.
16.(1)
(2)
(3)
(1)解:如图,连接,
在中,,
又∵,
∴是等边三角形,
∴,
∵,
∴的长;
(2)解:∵,
∴,
∴,
∵在中,,
∴;
(3)解:如图,连接,
∵,,
∴,
∴,
∵是的切线,
∴,,
∴,
∵,
∴,
∴,
∴.
17.(1),,
(2)抛物线和的顶点坐标分别为,, 的表达式为;的表达式为;
(3)
(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,
解得,
则抛物线的表达式为;
将代入,
解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,
∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,
解得:或(在对称轴右侧,舍),
∴,
由抛物线对称性可得.
18.(1)①,理由略;②
(2)
(1)解:①由翻折得,,
∵四边形是平行四边形,
∴,,
∴,,
又∵,
∴,
∴;
②由,
∴,
如图,过点作于点,过点作于点,
∴,
∵,,
∴,
∴,
∴,
∴,
∴;
(2)解:过点作于点,连接交于点,过点作于点,
由翻折的性质得,
同(2)可得,
∴,
∴,
即,
得,
∴,
∵平行四边形中,,,
∴,
又∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
即,
解得:.
一、单选题
1.我国是历史上最早认识和使用负数的国家.若盈利元记作元,则亏损元应记作( )
A.元 B.元 C.元 D.元
2.下列汽车电子控制装置显示的图案中,是中心对称图形的为( )
A. B. C. D.
3.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,的顶点坐标分别是,,,以原点为位似中心,在第三象限画与位似,若与的相似比为,则点的对应点的坐标为( )
A. B. C. D.
5.如图,是一个矩形草坪,对角线,相交于点,是边的中点,连接,且,,则该草坪的面积为( )
A. B. C. D.
6.如图,直线,点,分别在直线,上,连接,以点为圆心,适当长为半径画弧.交射线于点,交于点,再分别以点,为圆心,大于的长为半径画弧(两弧半径相等),两弧在的内部相交于点,画射线交于点,若,则的度数为( )
A. B. C. D.
7.在闭合电路中,通过定值电阻的电流(单位:A)是它两端的电压(单位:)的正比例函数,其图象如图所示,当该电阻两端的电压为时,通过它的电流为( )
A. B. C. D.
8.已知点,都在反比例函数的图象上,则下列结论一定正确的是( )
A. B.
C.当时, D.当时,
二、填空题
9.在单词(班级)中随机选择一个字母,则选中字母“”的概率是 .
10.冰糖葫芦是我国传统小吃,若大串冰糖葫芦每根穿5个山楂,小串冰糖葫芦每根穿3个山楂,则穿根大串和根小串冰糖葫芦需要的山楂总个数用代数式表示为 .
11.如图,因地形原因,湖泊两端,的距离不易测量,某科技小组需要用无人机进行测量.他们将无人机上升并飞行至距湖面的点处.从点测得点的俯角为,测得点的俯角为(,,三点在同一竖直平面内),则湖泊两端,的距离为 (结果保留根号).
12.如图,在菱形中,,对角线的长为,是的中点,是上一点,连接.若,则的长为 .
三、解答题
13.计算:
(1);
(2).
14.每年的6月6日是全国爱眼日,某校为了解八年级学生的视力健康状况,从该年级学生今年的体检结果中随机抽取了40名学生的视力数据,将所得视力数据进行整理后分为5组,得到如下的频数分布表:
分组 A B C D E
人数(频数) 2 8 14 12 4
请根据所给信息,解答下列问题:
(1)这40名学生视力的中位数落在哪个组内
(2)该校八年级共有500名学生.
①根据上表数据,请估计这500名八年级学生的视力在范围内的人数;
②从去年同期这500名学生的体检结果中可知,视力在范围内的人数为263人.如果你是该校的一名学生,请说明这500名学生今年和去年视力在范围内的人数变化情况,并为学校提一条保护学生视力的合理化建议.
15.智能机器人的广泛应用是智慧农业的发展趋势之一.某品牌苹果采摘机器人的机械手能自动对成熟的苹果进行采摘,一个机器人可以搭载多个机械手同时工作.在正常工作状态下,该机器人的每一个机械手平均秒采摘一个成熟的苹果,它的一个机械手用800秒采摘苹果的个数比用600秒采摘苹果的个数多25个.
(1)求的值;
(2)现需要一定数量的苹果发往外地,采摘工作由多个机器人共同完成.每个机器人搭载4个相同的机械手,那么至少需要多少个这样的机器人同时工作1小时,才能使采摘的苹果个数不少于10000个
16.如图,是的直径,半径,垂足为,,是延长线上一点,连接,交于点,连接,.过点作的切线,切点为,交的延长线于点.
(1)求的长;
(2)求的度数;
(3)求的值.
17.问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
18.如图,是一个平行四边形纸片,是一条对角线,,.
(1)如图1,将平行四边形纸片沿折叠,点的对应点落在点处,交于点.
①试猜想与的数量关系,并说明理由;
②求的面积;
(2)如图2,点,分别在平行四边形纸片的,边上,连接,且,将平行四边形纸片沿折叠,使点的对应点落在边上,求的长.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B B C B C D A D
9.
10./
11.
12.
13.(1)
(2)
(1)解:
;
(2)解:
.
14.(1)组
(2)①200人;②合理即可
(1)解:∵随机抽取了40名学生,
∴中位数为第名学生的视力的平均数,
由频数分布表可得第名学生在组,
∴这40名学生视力的中位数落在组;
(2)解:①由题意得,(人)
答:500名八年级学生的视力在范围内有200人;
②因为,
所以今年学生视力在范围内的人数相比去年减少,
建议:①读书时,坐姿要端正,不要在光线不好的地方看书;②保证充足的睡眠,饮食均衡;③减少电子产品的使用(合理即可).
15.(1)8
(2)至少需要6个这样的机器人
(1)解:由题意得,,
解得:,
经检验:是原方程的解,且符合题意,
∴的值为8;
(2)解:1小时,
设需要个这样的机器人,
由题意得:,
解得:,
∵为正整数,
∴最小值为6,
答:至少需要6个这样的机器人.
16.(1)
(2)
(3)
(1)解:如图,连接,
在中,,
又∵,
∴是等边三角形,
∴,
∵,
∴的长;
(2)解:∵,
∴,
∴,
∵在中,,
∴;
(3)解:如图,连接,
∵,,
∴,
∴,
∵是的切线,
∴,,
∴,
∵,
∴,
∴,
∴.
17.(1),,
(2)抛物线和的顶点坐标分别为,, 的表达式为;的表达式为;
(3)
(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,
解得,
则抛物线的表达式为;
将代入,
解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,
∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,
解得:或(在对称轴右侧,舍),
∴,
由抛物线对称性可得.
18.(1)①,理由略;②
(2)
(1)解:①由翻折得,,
∵四边形是平行四边形,
∴,,
∴,,
又∵,
∴,
∴;
②由,
∴,
如图,过点作于点,过点作于点,
∴,
∵,,
∴,
∴,
∴,
∴,
∴;
(2)解:过点作于点,连接交于点,过点作于点,
由翻折的性质得,
同(2)可得,
∴,
∴,
即,
得,
∴,
∵平行四边形中,,,
∴,
又∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
即,
解得:.
同课章节目录
