期末综合试题 2024-2025学年下期小学数学人教版五年级下册
文档属性
| 名称 | 期末综合试题 2024-2025学年下期小学数学人教版五年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 514.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 16:35:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末综合试题 2024-2025学年
下期小学数学人教版五年级下册
一、选择题
1.下列物体中,( )的体积最接近1cm 。
A. B. C. D.
2.一瓶“可口可乐”饮料有220( )。
A.升 B.毫升 C.立方分米 D.立方米
3.下列各组数中,( )的第一个数是第二个数的倍数。
A.6和12 B.16和6 C.36和0.6 D.24和8
4.如果是真分数,是假分数,那么n表示的整数最多有( )。
A.3个 B.2个 C.4个 D.无数个
5.下面的平面图中,( )号不能折成正方体。
A. B. C.
6.“哥德巴赫猜想”被誉为“数学皇冠上的明珠”,内容是“任何大于2的偶数都可以表示成两个质数之和”。下面所举的四个例子,符合哥德巴赫猜想的是( )。
A.6=1+5 B.7=2+5 C.10=3+7 D.12=4+8
二、填空题
7.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
8.下面的这段话中,出现了一些自然数,请认真阅读,完成下面的问题。
2025年4月24日,搭载神舟二十号载人飞船的长征二号F遥二十运载火箭在酒泉卫星发射中心点火发射成功。此次任务是我国载人航天工程进入空间站应用与发展阶段的第5次载人飞行任务,是工程立项实施以来的第35次发射任务,截至目前,我国已有26名航天员、41人次进入太空执行飞行任务。
这些划横线的自然数中偶数有( )个,质数有( )个,既是3的倍数又是5的倍数的数是( ),其中5和35的最大公因数是( )。
9.如图,把长方形看作“1”,那么阴影部分用分数表示是( ),用小数表示是( ),用除法算式表示是( )÷24。
10.如果是假分数,那么最大是( );如果是真分数,那么最小是( )。
11.某区的109路公交车每12分钟发一次车,102路公交车每15分钟发一次车,这两路车每天早上6:10在同一起点同时发车,下一次同时发车时间是( )。
12.将一根3米长的铁丝围成一个正方体框架,正方体的棱长为( )米,每条棱长是这根铁丝的。
13.如图,一条水管2小时可将小水槽注满,用同一条水管将大水池注满需( )小时。
14.在修复一处古代宫殿时,将一块长方体木料沿高截去2厘米,就变成一个正方体,表面积比原来减少了48平方厘米,正方体的表面积是( )平方厘米。
15.一个最简分数,如果分子加1,分数就等于1;如果分母加3,分数就等于。原来分数是( )。
16.如图,图①是一个盛满水的无盖长方体容器,水深,将容器如图②所示倾斜倒出一部分水,此时的长度是,再把容器放平,如图③所示,这时容器中水的深度是( )cm。
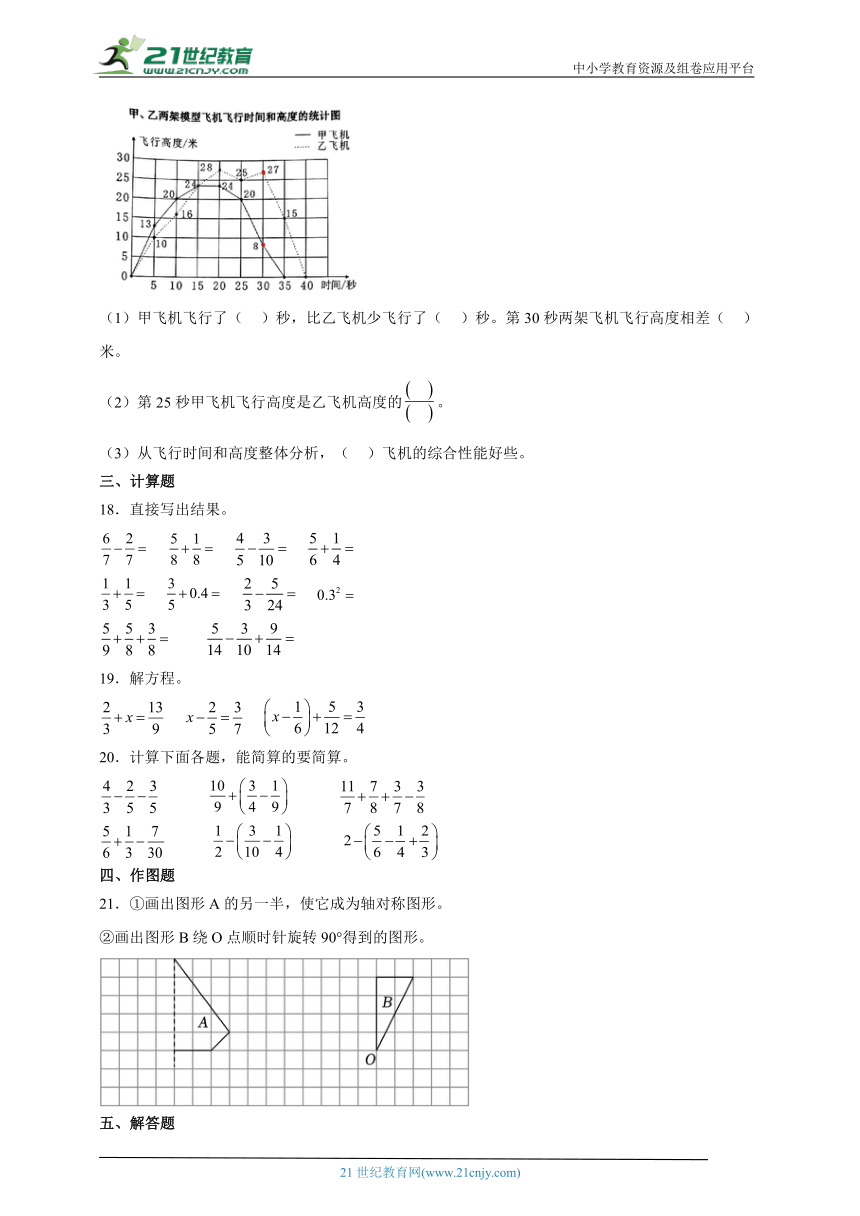
17.航模小组制作了甲、乙两架模型飞机,对两架模型飞机在一次飞行中飞行时间和高度进行记录,绘制了如下统计图。请根据图中的信息,解答下列问题。
(1)甲飞机飞行了( )秒,比乙飞机少飞行了( )秒。第30秒两架飞机飞行高度相差( )米。
(2)第25秒甲飞机飞行高度是乙飞机高度的。
(3)从飞行时间和高度整体分析,( )飞机的综合性能好些。
三、计算题
18.直接写出结果。
19.解方程。
20.计算下面各题,能简算的要简算。
四、作图题
21.①画出图形A的另一半,使它成为轴对称图形。
②画出图形B绕O点顺时针旋转90°得到的图形。
五、解答题
22.五(1)班有42人,大课间分组活动,每组人数相等且超过2人(组数大于1)。可以分成几组?每组几人?
23.一个长方体鱼缸,从内部量长6分米,宽4分米,高3分米,水深2分米。放入一块珊瑚石后,水面上升到2.5分米。珊瑚石的体积是多少?
24.修一条路,第一天修了全长的,第二天修了全长的,还剩全长的几分之几未修?
25.用铁丝焊接一个棱长总和为60厘米的正方体框架,至少需要多长的铁丝?如果用彩纸包装,至少需要多少平方厘米彩纸?
26.有两根钢管,一根长36分米,另一根长48分米。现在要把它们截成同样长的小段且无剩余,每段最长多少分米?一共能截多少段?
参考答案
题号 1 2 3 4 5 6
答案 B B D C B C
1.B
【分析】常见的体积单位有立方厘米、立方分米、立方米。立方厘米用字母表示是cm3,立方分米用字母表示是dm3,立方米用字母表示是m3。棱长1厘米的正方体,体积是1立方厘米;棱长1分米的正方体,体积是1立方分米;棱长1米的正方体,体积是1立方米。一个骰子的体积接近1立方厘米;一个粉笔盒的体积接近1立方分米;一个电视纸箱的体积接近1立方米。
【详解】A.计算器体积约200cm3。
B.游戏用的骰子体积约为1cm3。
C.一桶油约的体积约是5dm3。
D.一个苹果的体积约为1dm3。
骰子体积最接近1cm3。
故答案为:B
2.B
【分析】一瓶“可口可乐”饮料瓶容积比较小,用毫升作单位比较合适,据此解答即可。
【详解】一瓶“可口可乐”饮料有220毫升。
故答案为:B
【点睛】本题考查容积单位,解答本题的关键是掌握根据实际问题选择合适的容积单位。
3.D
【分析】用第一个数除以第二个数,被除数和除数都是整数,且商是整数且没有余数,则第一个数是第二个数的倍数。据此选择即可。
【详解】A.6÷12=0.5,第一个数不是第二个数的倍数;
B.16÷6=2……4,第一个数不是第二个数的倍数;
C.因为0.6不是整数,所以第一个数不是第二个数的倍数;
D.24÷8=3,所以第一个数是第二个数的倍数。
故答案为:D
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
4.C
【分析】分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
根据题意,是真分数,分子是4的真分数,那么分母必须大于4;是假分数,分子是8的假分数,那么分母必须小于或等于8;据此找出n表示的整数最多的个数。
【详解】如果是真分数,则n>4;
是假分数,则n≤8;
4<n≤8的数有:5,6,7,8;共4个。
所以n表示的整数最多有4个。
故答案为:C
【点睛】本题考查真分数和假分数的意义及实际应用。
5.B
【分析】根据正方体展开图的特点,“1—4—1”型、“2—3—1”型、“2—2—2”型、“3—3”型可以折成正方体;据此解答。
【详解】
A.,属于“1—4—1”型,是正方体的展开图,能折成正方体;
B.,不是正方体的展开图,不能折成正方体;
C.,属于“2—3—1”型,是正方体的展开图,能折成正方体;
故答案为:B
【点睛】运用空间想象力,结合正方体的展开图的特点以及正方体的特征进行解答。
6.C
【分析】是2的倍数的数叫做偶数(0也是偶数);只有1和它本身两个因数的数叫做质数,据此定义即可作出选择。
【详解】A.6=1+5中1既不是质数也不是偶数,不符合;
B.7=2+5中7不是偶数,不符合;
C.10=3+7中10是大于2的偶数,3和7都是质数,符合;
D.12=4+8中4和8都是合数,不符合。
故答案为:C
【点睛】掌握偶数、质数的定义,理解好“任何大于2的偶数都可以表示成两个质数之和”的意思,这是解决此题的关键。
7. 5 9
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。对于真分数、假分数来说,分子是几,就有几个这样的分数单位。
最小的质数是2,先把2化成分母为7而大小不变的假分数,再看分子与的分子相差几,就需要再添上几个这样的分数单位就是最小的质数。
【详解】里面有5个;
最小的质数是2;
2=,里面有14个;
14-5=9(个)
的分数单位是,它有5个这样的分数单位,再添上9个这样的分数单位就是最小的质数。
8.
3
2
2025
5
【分析】能被2整除的整数叫做偶数;一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;5的倍数的数的特征是个位数字是0或5,3的倍数的数的特征是各位数字之和能被3整除;两个或多个自然数公因数中最大的一个叫做最大公因数,可使用分解质因数法求最大公因数;根据概念逐一分析划横线的自然数2025、4、24、5、35、26、41,分别选出符合条件的数字。
【详解】4÷2=2,24÷2=12,26÷2=13,所以4、24、26是偶数,共3个;
5除了1和它本身外,不能被其他自然数整除;41除了1和它本身外,不能被其他自然数整除,所以5、41是质数,共2个;
2025个位是5,2+0+2+5=9,9÷3=3,能被3整除,所以2025既是3的倍数又是5的倍数;
35=5×7,所以5和35的最大公因数是5。
因此这些划横线的自然数中偶数有3个,质数有2个,既是3的倍数又是5的倍数的数是2025,其中5和35的最大公因数是5。
9. 0.375 9
【分析】求阴影部分用分数表示的结果:把长方形看作“1”,观察图形可知长方形被平均分成了8份,阴影部分占3份,根据分数的定义,阴影部分用分数表示为。
求阴影部分用小数表示的结果:分数号化为小数,用分子除以分母,即3÷8=0.375,所以阴影部分用小数表示为0.375。求除法算式中的被除数:设除法算式中被除数为x,根据分数与除法的关系=x÷24,由商不变的性质,24÷8=3,则x=3×3=9,即除法算式表示为9÷24。
【详解】=3÷8=0.375
解:设除法算式中被除数为x,
x÷24==3÷8=(3×3)÷(8×3)=9÷24
所以x=24
把长方形看作“1”,那么阴影部分用分数表示是,用小数表示是0.375,用除法算式表示是9÷24。
10. 7 8
【分析】要使是假分数,则a为等于或小于7整数;要使是真分数,则a为大于7的任意一个整数。据此填空即可。
【详解】是假分数,a 是整数且a≤7,最大是7;
是真分数,a 是整数且a>7,最小为8。
【点睛】此题主要利用真分数与假分数的意义进行解答即可。
11.7:10/7时10分
【分析】 发车间隔分析:109路每12分钟发车,102路每15分钟发车。 最小公倍数应用:求12和15的最小公倍数,得到两车同时发车的间隔时间。 时间计算:从首次同时发车时间6:10开始,加上间隔时间。
【详解】(1)12和15的最小公倍数:60
(2)6时10分+60分=7时10分或7:10
下一次同时发车时间是7:10。
12.;
【分析】 正方体棱长计算:正方体有12条相等的棱,用3米铁丝围成框架,每条棱长为总长除以12。
分数关系理解:将整根铁丝看作单位“1”,用每条棱长除以铁丝全长,即可求出每条棱长占铁丝全长的几分之几。
【详解】(1)棱长计算:3÷12=0.25(米)或(米)
(2)分数计算:÷3=×=
正方体的棱长为米,每条棱长是这根铁丝的。
13.24
【分析】已知小水槽长5m、宽4m、高3m,根据“长方体体积=长×宽×高”计算出小水槽的容积;已知注满小水槽需2小时,根据“注水速度=体积÷时间”,可得水管每小时注水的体积;已知大水池长12m、宽10m、高6m,根据长方体体积公式,计算出大水池容积;最后根据“时间=体积÷注水速度”,用大水池的体积除以注水速度计算出注满大水池需要的时间。
【详解】5×4×3
=20×3
=60(m3)
60÷2=30(m3)
12×10×6
=120×6
=720(m3)
720÷30=24(小时)
所以用同一条水管将大水池注满需24小时。
14.216
【分析】根据题意,将长方体沿高截去2厘米后变成正方体,表面积减少的部分是4个相同的长方形的面积之和。
用减少的表面积除以4,求出每个长方形的面积;长方形的宽为2厘米,长等于正方体的棱长,根据长方形的长=面积÷宽,据此求出正方体的棱长;
根据正方体的表面积=棱长×棱长×6,据此求出正方体的表面积。
【详解】每个长方形的面积:48÷4=12(平方厘米)
正方体的棱长:12÷2=6(厘米)
正方体的表面积:6×6×6=216(平方厘米)
正方体的表面积是216平方厘米。
15.
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。根据“如果分子加1,分数就等于1”可知,原分母比分子大1;已知如果分母加3,分数就等于,先根据分数的基本性质,把化成,分母6-3=3,3即是原来的分母,分数变成,4-3=1,分子比分母大1,不符合题意;同样把化成,分母9-3=6,6即是原来的分母,分数变成,6-6=0,分子等于分母,不符合题意;继续把化成,分母12-3=9,9即是原来的分母,分数变成,9-8=1,分母比分子大1,符合题意。
【详解】==
分母12-3=9,原来分数是,且9-8=1,分母比分子大1,符合题意。
所以原来分数是。
16.15
【分析】设长方体容器的长为a,宽为b。计算初始水的体积:初始水深24cm,根据长方体体积公式V=长×宽×高,则初始水的体积V=24ab。计算倒出部分水的体积:容器倾斜后,倒出部分水的体积相当于一个以ab为底面积,高为(24-6)cm的长方体体积的一半(因为倾斜后空白部分是三角形,其体积是对应长方体体积的一半)。倒出部分水的体积V=(24-6)×ab÷2=9ab。用24ab减去9ab求出剩余水的体积,再除以底面积即可求出放平后的水深。
【详解】解:设长方体容器的长为a,宽为b。
V=24ab
V=(24-6)×ab÷2=18×ab÷2=9ab
(24ab-9ab)÷ab
=15ab÷ab
=15(cm)
这时容器中水的深度是15cm。
【点睛】本题可根据长方体体积公式,结合倾斜前后水的体积变化来求解。
17.(1)35;5;19;
(2);
(3)乙
【分析】(1)计算飞行时间和高度差:甲飞机飞行到35秒落地,所以甲飞行了35秒;乙飞机飞行到40秒落地,甲比乙少飞行(40-35)秒。第30秒,甲飞机高度是8米,乙飞机高度是27米,相差(27-8)米。
(2)求第25秒甲、乙飞机高度的比例,第25秒,甲飞机高度是20米,乙飞机高度是25米,甲是乙的20÷25=,根据分数与除法的关系即可得解。
(3)分析综合性能:乙飞机飞行时间更长(40秒>35秒),且多数时间飞行高度不低于甲飞机,所以乙飞机综合性能好些。
【详解】(1)40-35=5(秒)
27-8=19(米)
甲飞机飞行了35秒,比乙飞机少飞行了5秒。第30秒两架飞机飞行高度相差19米。
(2)20÷25==
第25秒甲飞机飞行高度是乙飞机高度的。
(3)根据分析得,从飞行时间和高度整体分析,乙飞机的综合性能好些。
18.
; ;; ;
;1;;0.09;
;
【解析】略
19.;;
【分析】根据等式的性质1,方程两边同时减去,即可得解;
根据等式的性质1,方程两边同时加上,即可得解;
根据等式的性质1,方程两边先同时减去,再加上,即可得解。
【详解】
解:
解:
解:
20.;;
;;
【分析】(1)根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(2)先去掉括号把算式变成,再交换“”和“”的位置进行简算;
(3)先交换“”和“”的位置,把算式变成,再根据加法结合律(a+b)+c=a+(b+c)把算式变成进行简算;
(4)从左往右依次计算;
(5)先算括号里面的减法,再算括号外面的减法;
(6)先算括号里面的减法,再算括号里面的加法,最后算括号外面的减法。
【详解】(1)
(2)
(3)
(4)
(5)
(6)
21.见详解
【分析】①轴对称图形对应点到对称轴的距离相等,对应点的连线垂直于对称轴,据此作图画出A的另一半;
②点O不动,将图形的各边均顺时针旋转90°,画出旋转后的图形。
【详解】如图:
【点睛】本题考查了轴对称和旋转,掌握轴对称图形和旋转的作图方法是解题的关键。
22.分成14组,每组3人;分成7组,每组6人;分成6组,每组7人;分成3组,每组14人;分成2组,每组21人
【分析】分析题目,先找出42的因数,则每组人数是42的因数中大于2且小于42的数,据此确定每组的人数,最后用总人数除以每组人数即可得到分成的组数。
【详解】42=1×42=2×21=3×14=6×7
42的因数有:1,2,3,6,7,14,21,42;
每组的人数可能是3,6,7,14,21;
42÷3=14(组)
42÷6=7(组)
42÷7=6(组)
42÷14=3(组)
42÷21=2(组)
答:可以分成14组,每组3人;分成7组,每组6人;分成6组,每组7人;分成3组,每组14人;分成2组,每组21人。
23.12立方分米
【分析】分析题目,珊瑚石的体积等于长是6分米宽是4分米高是(2.5-2)分米的长方体的体积,根据长方体的体积=长×宽×高代入数据列式计算即可。
【详解】6×4×(2.5-2)
=6×4×0.5
=24×0.5
=12(立方分米)
答:珊瑚石的体积是12立方分米。
24.
【分析】将全长看作单位“1”,1-第一天修了全长的几分之几-第二天修了全长的几分之几=还剩全长的几分之几未修。
【详解】1--
=-
=-
=
答:还剩全长的未修。
25.60厘米;150平方厘米
【分析】铁丝长度相当于正方体棱长总和,正方体棱长=棱长总和÷12,正方体表面积=棱长×棱长×6,据此列式解答。
【详解】棱长:60÷12=5(厘米)
表面积:5×5×6=150(平方厘米)
答:至少需要60厘米的铁丝,如果用彩纸包装,至少需要150平方厘米彩纸。
26.12分米;7段
【分析】截成同样长的小段,且没有剩余,说明每段钢管是36和48的公因数,求最长是多少米,则是求36和48的最大公因数,再用36除以最大公因数的商加上48除以最大公因数的商,即是一共截成的段数,列式解答即可得到答案。
【详解】36=2×2×3×3
48=2×2×2×2×3
36和48的最大公因数为:2×2×3=12
所以每小段最长是12分米
36÷12+48÷12
=3+4
=7(段)
答:每小段彩带最长是12分米,一共可以截成7段。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合试题 2024-2025学年
下期小学数学人教版五年级下册
一、选择题
1.下列物体中,( )的体积最接近1cm 。
A. B. C. D.
2.一瓶“可口可乐”饮料有220( )。
A.升 B.毫升 C.立方分米 D.立方米
3.下列各组数中,( )的第一个数是第二个数的倍数。
A.6和12 B.16和6 C.36和0.6 D.24和8
4.如果是真分数,是假分数,那么n表示的整数最多有( )。
A.3个 B.2个 C.4个 D.无数个
5.下面的平面图中,( )号不能折成正方体。
A. B. C.
6.“哥德巴赫猜想”被誉为“数学皇冠上的明珠”,内容是“任何大于2的偶数都可以表示成两个质数之和”。下面所举的四个例子,符合哥德巴赫猜想的是( )。
A.6=1+5 B.7=2+5 C.10=3+7 D.12=4+8
二、填空题
7.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
8.下面的这段话中,出现了一些自然数,请认真阅读,完成下面的问题。
2025年4月24日,搭载神舟二十号载人飞船的长征二号F遥二十运载火箭在酒泉卫星发射中心点火发射成功。此次任务是我国载人航天工程进入空间站应用与发展阶段的第5次载人飞行任务,是工程立项实施以来的第35次发射任务,截至目前,我国已有26名航天员、41人次进入太空执行飞行任务。
这些划横线的自然数中偶数有( )个,质数有( )个,既是3的倍数又是5的倍数的数是( ),其中5和35的最大公因数是( )。
9.如图,把长方形看作“1”,那么阴影部分用分数表示是( ),用小数表示是( ),用除法算式表示是( )÷24。
10.如果是假分数,那么最大是( );如果是真分数,那么最小是( )。
11.某区的109路公交车每12分钟发一次车,102路公交车每15分钟发一次车,这两路车每天早上6:10在同一起点同时发车,下一次同时发车时间是( )。
12.将一根3米长的铁丝围成一个正方体框架,正方体的棱长为( )米,每条棱长是这根铁丝的。
13.如图,一条水管2小时可将小水槽注满,用同一条水管将大水池注满需( )小时。
14.在修复一处古代宫殿时,将一块长方体木料沿高截去2厘米,就变成一个正方体,表面积比原来减少了48平方厘米,正方体的表面积是( )平方厘米。
15.一个最简分数,如果分子加1,分数就等于1;如果分母加3,分数就等于。原来分数是( )。
16.如图,图①是一个盛满水的无盖长方体容器,水深,将容器如图②所示倾斜倒出一部分水,此时的长度是,再把容器放平,如图③所示,这时容器中水的深度是( )cm。
17.航模小组制作了甲、乙两架模型飞机,对两架模型飞机在一次飞行中飞行时间和高度进行记录,绘制了如下统计图。请根据图中的信息,解答下列问题。
(1)甲飞机飞行了( )秒,比乙飞机少飞行了( )秒。第30秒两架飞机飞行高度相差( )米。
(2)第25秒甲飞机飞行高度是乙飞机高度的。
(3)从飞行时间和高度整体分析,( )飞机的综合性能好些。
三、计算题
18.直接写出结果。
19.解方程。
20.计算下面各题,能简算的要简算。
四、作图题
21.①画出图形A的另一半,使它成为轴对称图形。
②画出图形B绕O点顺时针旋转90°得到的图形。
五、解答题
22.五(1)班有42人,大课间分组活动,每组人数相等且超过2人(组数大于1)。可以分成几组?每组几人?
23.一个长方体鱼缸,从内部量长6分米,宽4分米,高3分米,水深2分米。放入一块珊瑚石后,水面上升到2.5分米。珊瑚石的体积是多少?
24.修一条路,第一天修了全长的,第二天修了全长的,还剩全长的几分之几未修?
25.用铁丝焊接一个棱长总和为60厘米的正方体框架,至少需要多长的铁丝?如果用彩纸包装,至少需要多少平方厘米彩纸?
26.有两根钢管,一根长36分米,另一根长48分米。现在要把它们截成同样长的小段且无剩余,每段最长多少分米?一共能截多少段?
参考答案
题号 1 2 3 4 5 6
答案 B B D C B C
1.B
【分析】常见的体积单位有立方厘米、立方分米、立方米。立方厘米用字母表示是cm3,立方分米用字母表示是dm3,立方米用字母表示是m3。棱长1厘米的正方体,体积是1立方厘米;棱长1分米的正方体,体积是1立方分米;棱长1米的正方体,体积是1立方米。一个骰子的体积接近1立方厘米;一个粉笔盒的体积接近1立方分米;一个电视纸箱的体积接近1立方米。
【详解】A.计算器体积约200cm3。
B.游戏用的骰子体积约为1cm3。
C.一桶油约的体积约是5dm3。
D.一个苹果的体积约为1dm3。
骰子体积最接近1cm3。
故答案为:B
2.B
【分析】一瓶“可口可乐”饮料瓶容积比较小,用毫升作单位比较合适,据此解答即可。
【详解】一瓶“可口可乐”饮料有220毫升。
故答案为:B
【点睛】本题考查容积单位,解答本题的关键是掌握根据实际问题选择合适的容积单位。
3.D
【分析】用第一个数除以第二个数,被除数和除数都是整数,且商是整数且没有余数,则第一个数是第二个数的倍数。据此选择即可。
【详解】A.6÷12=0.5,第一个数不是第二个数的倍数;
B.16÷6=2……4,第一个数不是第二个数的倍数;
C.因为0.6不是整数,所以第一个数不是第二个数的倍数;
D.24÷8=3,所以第一个数是第二个数的倍数。
故答案为:D
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
4.C
【分析】分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
根据题意,是真分数,分子是4的真分数,那么分母必须大于4;是假分数,分子是8的假分数,那么分母必须小于或等于8;据此找出n表示的整数最多的个数。
【详解】如果是真分数,则n>4;
是假分数,则n≤8;
4<n≤8的数有:5,6,7,8;共4个。
所以n表示的整数最多有4个。
故答案为:C
【点睛】本题考查真分数和假分数的意义及实际应用。
5.B
【分析】根据正方体展开图的特点,“1—4—1”型、“2—3—1”型、“2—2—2”型、“3—3”型可以折成正方体;据此解答。
【详解】
A.,属于“1—4—1”型,是正方体的展开图,能折成正方体;
B.,不是正方体的展开图,不能折成正方体;
C.,属于“2—3—1”型,是正方体的展开图,能折成正方体;
故答案为:B
【点睛】运用空间想象力,结合正方体的展开图的特点以及正方体的特征进行解答。
6.C
【分析】是2的倍数的数叫做偶数(0也是偶数);只有1和它本身两个因数的数叫做质数,据此定义即可作出选择。
【详解】A.6=1+5中1既不是质数也不是偶数,不符合;
B.7=2+5中7不是偶数,不符合;
C.10=3+7中10是大于2的偶数,3和7都是质数,符合;
D.12=4+8中4和8都是合数,不符合。
故答案为:C
【点睛】掌握偶数、质数的定义,理解好“任何大于2的偶数都可以表示成两个质数之和”的意思,这是解决此题的关键。
7. 5 9
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。对于真分数、假分数来说,分子是几,就有几个这样的分数单位。
最小的质数是2,先把2化成分母为7而大小不变的假分数,再看分子与的分子相差几,就需要再添上几个这样的分数单位就是最小的质数。
【详解】里面有5个;
最小的质数是2;
2=,里面有14个;
14-5=9(个)
的分数单位是,它有5个这样的分数单位,再添上9个这样的分数单位就是最小的质数。
8.
3
2
2025
5
【分析】能被2整除的整数叫做偶数;一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;5的倍数的数的特征是个位数字是0或5,3的倍数的数的特征是各位数字之和能被3整除;两个或多个自然数公因数中最大的一个叫做最大公因数,可使用分解质因数法求最大公因数;根据概念逐一分析划横线的自然数2025、4、24、5、35、26、41,分别选出符合条件的数字。
【详解】4÷2=2,24÷2=12,26÷2=13,所以4、24、26是偶数,共3个;
5除了1和它本身外,不能被其他自然数整除;41除了1和它本身外,不能被其他自然数整除,所以5、41是质数,共2个;
2025个位是5,2+0+2+5=9,9÷3=3,能被3整除,所以2025既是3的倍数又是5的倍数;
35=5×7,所以5和35的最大公因数是5。
因此这些划横线的自然数中偶数有3个,质数有2个,既是3的倍数又是5的倍数的数是2025,其中5和35的最大公因数是5。
9. 0.375 9
【分析】求阴影部分用分数表示的结果:把长方形看作“1”,观察图形可知长方形被平均分成了8份,阴影部分占3份,根据分数的定义,阴影部分用分数表示为。
求阴影部分用小数表示的结果:分数号化为小数,用分子除以分母,即3÷8=0.375,所以阴影部分用小数表示为0.375。求除法算式中的被除数:设除法算式中被除数为x,根据分数与除法的关系=x÷24,由商不变的性质,24÷8=3,则x=3×3=9,即除法算式表示为9÷24。
【详解】=3÷8=0.375
解:设除法算式中被除数为x,
x÷24==3÷8=(3×3)÷(8×3)=9÷24
所以x=24
把长方形看作“1”,那么阴影部分用分数表示是,用小数表示是0.375,用除法算式表示是9÷24。
10. 7 8
【分析】要使是假分数,则a为等于或小于7整数;要使是真分数,则a为大于7的任意一个整数。据此填空即可。
【详解】是假分数,a 是整数且a≤7,最大是7;
是真分数,a 是整数且a>7,最小为8。
【点睛】此题主要利用真分数与假分数的意义进行解答即可。
11.7:10/7时10分
【分析】 发车间隔分析:109路每12分钟发车,102路每15分钟发车。 最小公倍数应用:求12和15的最小公倍数,得到两车同时发车的间隔时间。 时间计算:从首次同时发车时间6:10开始,加上间隔时间。
【详解】(1)12和15的最小公倍数:60
(2)6时10分+60分=7时10分或7:10
下一次同时发车时间是7:10。
12.;
【分析】 正方体棱长计算:正方体有12条相等的棱,用3米铁丝围成框架,每条棱长为总长除以12。
分数关系理解:将整根铁丝看作单位“1”,用每条棱长除以铁丝全长,即可求出每条棱长占铁丝全长的几分之几。
【详解】(1)棱长计算:3÷12=0.25(米)或(米)
(2)分数计算:÷3=×=
正方体的棱长为米,每条棱长是这根铁丝的。
13.24
【分析】已知小水槽长5m、宽4m、高3m,根据“长方体体积=长×宽×高”计算出小水槽的容积;已知注满小水槽需2小时,根据“注水速度=体积÷时间”,可得水管每小时注水的体积;已知大水池长12m、宽10m、高6m,根据长方体体积公式,计算出大水池容积;最后根据“时间=体积÷注水速度”,用大水池的体积除以注水速度计算出注满大水池需要的时间。
【详解】5×4×3
=20×3
=60(m3)
60÷2=30(m3)
12×10×6
=120×6
=720(m3)
720÷30=24(小时)
所以用同一条水管将大水池注满需24小时。
14.216
【分析】根据题意,将长方体沿高截去2厘米后变成正方体,表面积减少的部分是4个相同的长方形的面积之和。
用减少的表面积除以4,求出每个长方形的面积;长方形的宽为2厘米,长等于正方体的棱长,根据长方形的长=面积÷宽,据此求出正方体的棱长;
根据正方体的表面积=棱长×棱长×6,据此求出正方体的表面积。
【详解】每个长方形的面积:48÷4=12(平方厘米)
正方体的棱长:12÷2=6(厘米)
正方体的表面积:6×6×6=216(平方厘米)
正方体的表面积是216平方厘米。
15.
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。根据“如果分子加1,分数就等于1”可知,原分母比分子大1;已知如果分母加3,分数就等于,先根据分数的基本性质,把化成,分母6-3=3,3即是原来的分母,分数变成,4-3=1,分子比分母大1,不符合题意;同样把化成,分母9-3=6,6即是原来的分母,分数变成,6-6=0,分子等于分母,不符合题意;继续把化成,分母12-3=9,9即是原来的分母,分数变成,9-8=1,分母比分子大1,符合题意。
【详解】==
分母12-3=9,原来分数是,且9-8=1,分母比分子大1,符合题意。
所以原来分数是。
16.15
【分析】设长方体容器的长为a,宽为b。计算初始水的体积:初始水深24cm,根据长方体体积公式V=长×宽×高,则初始水的体积V=24ab。计算倒出部分水的体积:容器倾斜后,倒出部分水的体积相当于一个以ab为底面积,高为(24-6)cm的长方体体积的一半(因为倾斜后空白部分是三角形,其体积是对应长方体体积的一半)。倒出部分水的体积V=(24-6)×ab÷2=9ab。用24ab减去9ab求出剩余水的体积,再除以底面积即可求出放平后的水深。
【详解】解:设长方体容器的长为a,宽为b。
V=24ab
V=(24-6)×ab÷2=18×ab÷2=9ab
(24ab-9ab)÷ab
=15ab÷ab
=15(cm)
这时容器中水的深度是15cm。
【点睛】本题可根据长方体体积公式,结合倾斜前后水的体积变化来求解。
17.(1)35;5;19;
(2);
(3)乙
【分析】(1)计算飞行时间和高度差:甲飞机飞行到35秒落地,所以甲飞行了35秒;乙飞机飞行到40秒落地,甲比乙少飞行(40-35)秒。第30秒,甲飞机高度是8米,乙飞机高度是27米,相差(27-8)米。
(2)求第25秒甲、乙飞机高度的比例,第25秒,甲飞机高度是20米,乙飞机高度是25米,甲是乙的20÷25=,根据分数与除法的关系即可得解。
(3)分析综合性能:乙飞机飞行时间更长(40秒>35秒),且多数时间飞行高度不低于甲飞机,所以乙飞机综合性能好些。
【详解】(1)40-35=5(秒)
27-8=19(米)
甲飞机飞行了35秒,比乙飞机少飞行了5秒。第30秒两架飞机飞行高度相差19米。
(2)20÷25==
第25秒甲飞机飞行高度是乙飞机高度的。
(3)根据分析得,从飞行时间和高度整体分析,乙飞机的综合性能好些。
18.
; ;; ;
;1;;0.09;
;
【解析】略
19.;;
【分析】根据等式的性质1,方程两边同时减去,即可得解;
根据等式的性质1,方程两边同时加上,即可得解;
根据等式的性质1,方程两边先同时减去,再加上,即可得解。
【详解】
解:
解:
解:
20.;;
;;
【分析】(1)根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(2)先去掉括号把算式变成,再交换“”和“”的位置进行简算;
(3)先交换“”和“”的位置,把算式变成,再根据加法结合律(a+b)+c=a+(b+c)把算式变成进行简算;
(4)从左往右依次计算;
(5)先算括号里面的减法,再算括号外面的减法;
(6)先算括号里面的减法,再算括号里面的加法,最后算括号外面的减法。
【详解】(1)
(2)
(3)
(4)
(5)
(6)
21.见详解
【分析】①轴对称图形对应点到对称轴的距离相等,对应点的连线垂直于对称轴,据此作图画出A的另一半;
②点O不动,将图形的各边均顺时针旋转90°,画出旋转后的图形。
【详解】如图:
【点睛】本题考查了轴对称和旋转,掌握轴对称图形和旋转的作图方法是解题的关键。
22.分成14组,每组3人;分成7组,每组6人;分成6组,每组7人;分成3组,每组14人;分成2组,每组21人
【分析】分析题目,先找出42的因数,则每组人数是42的因数中大于2且小于42的数,据此确定每组的人数,最后用总人数除以每组人数即可得到分成的组数。
【详解】42=1×42=2×21=3×14=6×7
42的因数有:1,2,3,6,7,14,21,42;
每组的人数可能是3,6,7,14,21;
42÷3=14(组)
42÷6=7(组)
42÷7=6(组)
42÷14=3(组)
42÷21=2(组)
答:可以分成14组,每组3人;分成7组,每组6人;分成6组,每组7人;分成3组,每组14人;分成2组,每组21人。
23.12立方分米
【分析】分析题目,珊瑚石的体积等于长是6分米宽是4分米高是(2.5-2)分米的长方体的体积,根据长方体的体积=长×宽×高代入数据列式计算即可。
【详解】6×4×(2.5-2)
=6×4×0.5
=24×0.5
=12(立方分米)
答:珊瑚石的体积是12立方分米。
24.
【分析】将全长看作单位“1”,1-第一天修了全长的几分之几-第二天修了全长的几分之几=还剩全长的几分之几未修。
【详解】1--
=-
=-
=
答:还剩全长的未修。
25.60厘米;150平方厘米
【分析】铁丝长度相当于正方体棱长总和,正方体棱长=棱长总和÷12,正方体表面积=棱长×棱长×6,据此列式解答。
【详解】棱长:60÷12=5(厘米)
表面积:5×5×6=150(平方厘米)
答:至少需要60厘米的铁丝,如果用彩纸包装,至少需要150平方厘米彩纸。
26.12分米;7段
【分析】截成同样长的小段,且没有剩余,说明每段钢管是36和48的公因数,求最长是多少米,则是求36和48的最大公因数,再用36除以最大公因数的商加上48除以最大公因数的商,即是一共截成的段数,列式解答即可得到答案。
【详解】36=2×2×3×3
48=2×2×2×2×3
36和48的最大公因数为:2×2×3=12
所以每小段最长是12分米
36÷12+48÷12
=3+4
=7(段)
答:每小段彩带最长是12分米,一共可以截成7段。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
