期末综合试题 2024-2025学年下期初中数学人教版七年级下册(新教材)
文档属性
| 名称 | 期末综合试题 2024-2025学年下期初中数学人教版七年级下册(新教材) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 16:35:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末综合试题 2024-2025学年下期初中
数学人教版七年级下册(新教材)
一、单选题
1.在实数,,,,,,(两个1之间依次多一个6)中,无理数的个数是( )
A.5 B.4 C.3 D.2
2.化简的结果是( )
A.3 B. C. D.9
3.以下调查中,适合全面调查的是( )
A.了解山西中学生的视力情况
B.检测临汾地区和运城地区的城市空气质量
C.调查汾河源头现有鱼的数量
D.调查某教研组老师是否参加新教材培训
4.如图,直线与交于点O,,若,则的度数为( )
A. B. C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.我国古代数学著作《算法统宗》中记载了这样一道题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?其大意为:用绳子测量井的深度,如果将绳子折成三等份,则一份绳长比井深多4尺,如果将绳子折成四等份,则一份绳长比井深多1尺,则绳长、井深各是多少尺?若设绳长x尺,井深y尺,则下列所列方程组正确的是( )
A. B. C. D.
7.如果关于的不等式的解集为,那么的取值范围是( )
A. B. C. D.
8.点P在第二象限内,点P到x轴的距离是6,到y轴的距离是2,那么点P的坐标为( )
A.(﹣6,2) B.(﹣2,﹣6) C.(﹣2,6) D.(2,﹣6)
9.如图,智能机器人从平面直角坐标系的原点O出发,向上走1个单位长度到达点,再向左走1个单位长度到达点,再向下走2个单位长度到达点,再向右走2个单位长度到达点,再向上走3个单位长度到达点,…以此规律走下去,当智能机器人到达点时,它的坐标为( )
A. B. C. D.
10.已知关于,的二元一次方程组给出下列结论中正确的是( )
①当时,方程组的解也是方程的解;
②无论取什么实数,的值始终不变;
③当时,.
A.①② B.①③ C.②③ D.①②③
二、填空题
11.计算:= .
12.在平面直角坐标系中,若将点先向上平移3个单位长度,再向右平移3个单位长度得到点,则点的坐标为 .
13.统计得到的一组数据最大值为139,最小值为48,取组距为10,可分成 组.
14.已知关于的方程组,若其解互为相反数,则的值为 .
15.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190”为一次操作.若操作恰好进行两次停止,则x的取值范围是 .
16.下列命题:①相等的角是对顶角;②算术平方根等于它本身的数有两个,分别是0和1;③已知关于的二元一次方程组,不论取什么有理数,的值始终不变;④已知正实数的平方根是和,若,则;⑤若不等式对一切实数都成立,则的最大值是5;
其中真命题是: .(请填序号)
三、解答题
17.计算:.
18.(1)解方程组:
(2)解不等式组:
19.如图,直线和相交于点,,若,求的度数.
20.在平面直角坐标系中,已知点,,现将线段按照某种方式进行平移,使点平移到点处,点平移到点处.
(1)画出平移后的线段,并写出点的坐标;
(2)连接,,求三角形的面积.
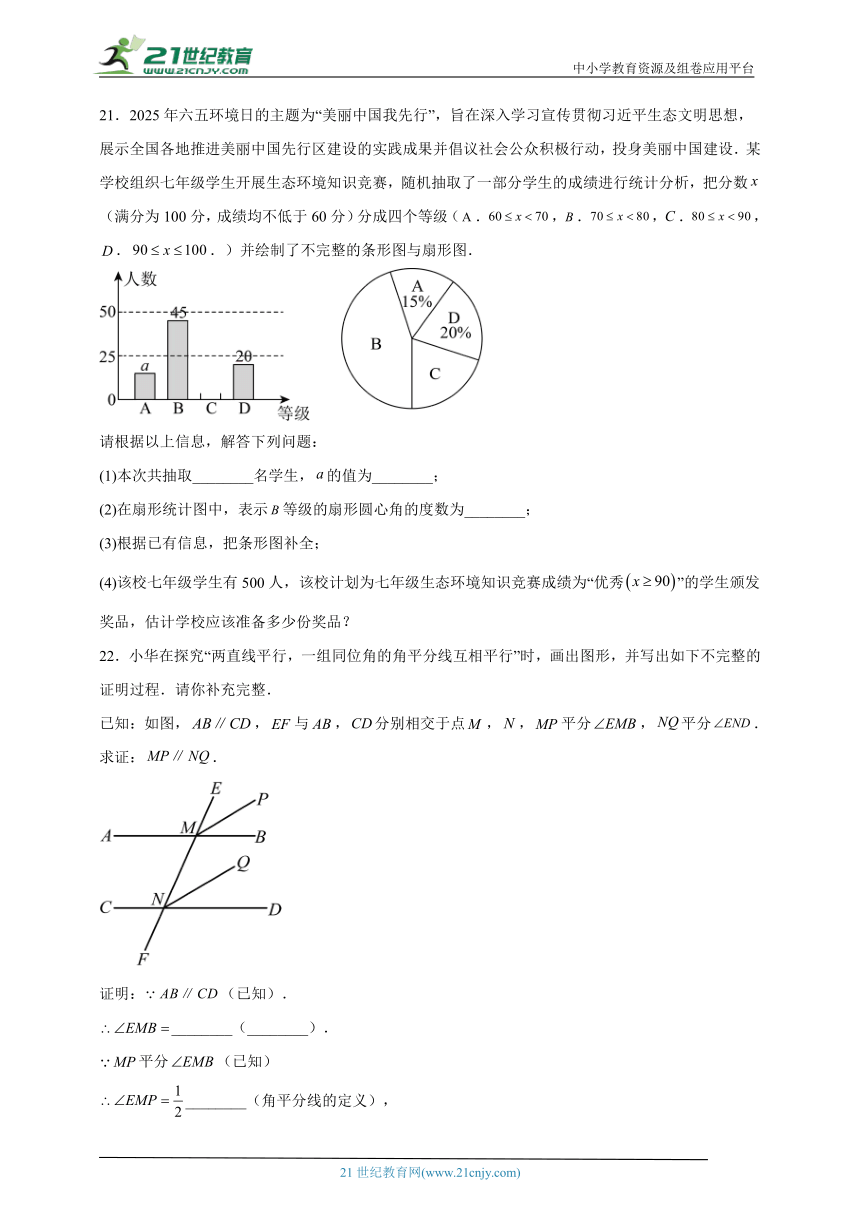
21.2025年六五环境日的主题为“美丽中国我先行”,旨在深入学习宣传贯彻习近平生态文明思想,展示全国各地推进美丽中国先行区建设的实践成果并倡议社会公众积极行动,投身美丽中国建设.某学校组织七年级学生开展生态环境知识竞赛,随机抽取了一部分学生的成绩进行统计分析,把分数(满分为100分,成绩均不低于60分)分成四个等级(.,.,.,..)并绘制了不完整的条形图与扇形图.
请根据以上信息,解答下列问题:
(1)本次共抽取________名学生,的值为________;
(2)在扇形统计图中,表示等级的扇形圆心角的度数为________;
(3)根据已有信息,把条形图补全;
(4)该校七年级学生有500人,该校计划为七年级生态环境知识竞赛成绩为“优秀”的学生颁发奖品,估计学校应该准备多少份奖品?
22.小华在探究“两直线平行,一组同位角的角平分线互相平行”时,画出图形,并写出如下不完整的证明过程.请你补充完整.
已知:如图,,与,分别相交于点,,平分,平分.
求证:.
证明:(已知).
________(________).
平分(已知)
________(角平分线的定义),
同理.
________(等式的性质).
(________).
23.国家主席习近平在2025年新年贺词中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.“今年某市计划引进,两种车型的新能源公交车,若购买型公交车2辆,型公交车3辆,共需360万元;若购买型公交车3辆,型公交车2辆,共需340万元
(1)求购买型和型新能源公交车每辆分别需要多少万元?
(2)若计划本批次购买型和型新能源公交车20辆,要求两种车型都要购买,且型新能源公交车的数量不超过型新能源公交车数量的,请写出花钱最少的购车方案.
24.【综合实践】——折纸中的数学
某兴趣小组在探究“过直线外一点作已知直线的平行线”的活动中,通过以下的折纸方式找符合要求的直线.如图①,在一张正方形纸片的两边上分别有,两点,连接,是正方形纸片上一点,用折纸的方法过点作的平行线的基本步骤如下:
第一步:如图②,过点进行第一次折叠,使点的对应点落在上,折痕与互相垂直,垂足为,打开纸张铺平;
第二步:如图③,过点进行第二次折叠,使折痕,打开纸张铺平(如图④).
(1)根据上述步骤可知,与的位置关系是________.
(2)如图④,设直线与正方形上、下两边分别交于点,,试探究与的数量关系,并说明理由.
25.如图,在平面直角坐标系中,已知点,,,其中是的立方根,且满足.
(1)直接写出、、三点坐标:___________,___________,___________;
(2)如图1,将三角形向左平移个单位,三角形被轴分成面积比为的两个部分,求的值.
(3)如图2,将线段向上平移2个单位长度,点为轴上一动点,点为第一象限内动点,且,连接,若,直接写出点的纵坐标(用含的式子表示).
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B B C A C A D
1.C
【分析】本题考查了无理数的定义,掌握无理数的常见形式“①最终结果含有开方开不尽的数,②最终结果含有的数,③形如(每两个增加一个).”是解题的关键.
【详解】解:是有限小数,0,3是整数,是分数,它们不是无理数;
,,(两个1之间依次多一个6)是无限不循环小数,它们是无理数,共3个;
故选:C.
2.A
【分析】本题考查算术平方根计算.根据题意先将根式中计算出来,再开根号即可得到本题答案.
【详解】解:,
故选:A.
3.D
【分析】根据抽样调查和全面调查的特点,选择合适的调查方式.本题考查了调查的两种方式,熟练掌握两种方式使用的基本特点是解题的关键.
【详解】解:了解山西中学生的视力情况,采用抽样调查方式,
∴A不符合题意;
检测临汾地区和运城地区的城市空气质量,采用抽样调查方式,
∴B不符合题意;
调查汾河源头现有鱼的数量,采用抽查方式,
∴C不符合题意;
调查某教研组老师是否参加新教材培训,采取全面调查的方式,
∴D符合题意;
故选:D.
4.B
【分析】直接利用邻补角的定义结合垂线的定义进而得出答案.
【详解】解:∵,
∴,
∵,
∴,
∴,故B正确.
故选:B.
【点睛】主要考查了邻补角和垂线的定义,正确得出的度数是解题关键.
5.B
【分析】本题主要考查了在数轴上表示不等式的解集,大于号,要向数轴右边画,且表示的点画空心圆圈,据此可得答案.
【详解】解:大于,则应从表示的点向右画,并且不包含的点,即表示的点画空心圆圈,即数轴表示如下:
故选:B.
6.C
【分析】本题主要考查了二元一次方程组的实际应用,设绳长x尺,井深y尺,根据将绳子折成三等份,则一份绳长比井深多4尺可得方程,根据将绳子折成四等份,则一份绳长比井深多1尺可得方程,据此列出方程组即可.
【详解】解:由题意得,,
故选:C.
7.A
【分析】利用不等式的基本性质求解即可.
【详解】解:∵不等式的解集为,
∴,
故选:A.
【点睛】本题考查不等式的基本性质、不等式的解集,熟练掌握不等式的基本性质的运用,注意符号的变化是解答的关键.
8.C
【分析】根据点(x,y)到x轴的距离为|y|,到y轴的距离|x|解答即可.
【详解】解:设点P坐标为(x,y),
∵点P到x轴的距离是6,到y轴的距离是2,
∴|y|=6,|x|=2,
∵点P在第二象限内,
∴y=6,x=-2,
∴点P坐标为(-2,6),
故选:C.
【点睛】本题考查点到坐标轴的距离、点所在的象限,熟知点到坐标轴的距离与坐标的关系是解答的关键.
9.A
【分析】本题主要考查坐标与图形变化-平移和找规律的知识点,熟悉平移规律和坐标系是解答本题的关键.
根据这些点的坐标找出某一象限点的坐标规律,最后判断所在象限,从而求出其坐标.
【详解】解:依题意可知:点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,且,
∴是第一象限的点,
∴的坐标是.
故选:A.
10.D
【分析】本题考查了含参二元一次方程组中参数的确定,二元一次方程组的解法,解一元一次不等式等知识,掌握二元一次方程组的解法是解题的关键.
解方程组得到,再逐项进行判断即可.
【详解】解:解方程组,得,
当时,,,代入得到,满足方程,结论①正确;
,与无关,始终为定值3,结论②正确;
若,即,解得:,
所以当时,成立,结论③正确;
综上,①②③均正确,
故选:D.
11.2
【分析】根据立方根的定义进行计算.
【详解】解:∵23=8,
∴,
故答案为:2.
12.
【分析】此题主要考查坐标与图形变化-平移,掌握点的坐标变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.利用点平移的坐标规律,把点的横坐标加3,纵坐标加3即可得到点的坐标.
【详解】解:∵将点先向上平移3个单位长度,再向右平移3个单位长度得到点,
∴点的坐标是,即.
故答案为:.
13.10
【分析】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数(最大值最小值)÷组距计算,注意小数部分要进位.
【详解】解:∵极差为,
∴由,
所以可分10组,
故答案为:10.
14.2
【分析】本题考查根据方程组的解的情况求参数,两个方程相减,结合互为相反数的两数之和为0,列出关于的一元一次方程,进行求解即可.
【详解】解:,
,得:,
∵互为相反数,
∴,
∴;
故答案为:2.
15./
【分析】根据第一次操作没有停止可得不等式,根据第二次操作后停止可得不等式,由此建立不等式组求解即可.
【详解】解:由题意得,,
解得,
故答案为:.
【点睛】本题主要考查了解一元一次不等式组,正确理解题意列出不等式组是解题的关键.
16.②③④
【分析】根据对顶角、平方根、解二元一次方程组、代数式求值、绝对值等知识逐项判断即可.
【详解】解:①对顶角一定相等,但相等的角不一定是对顶角,所以①是假命题;
②算术平方根等于它本身的数有两个,分别是0和1,即②是真命题.
③解方程组可得:,则,
所以不论取什么有理数,的值始终不变,③是真命题.
④因为正实数的平方根是和,
所以,即,且,
因为,
所以,即,
因为正实数,则,④是真命题.
⑤:设,
当时,;
当时,;
当时,.
所以的最小值是3,
若不等式对一切实数a都成立,则,即m的最大值是3,则⑤是假命题.
故答案为:②③④.
【点睛】本题主要考查了对顶角、平方根、解二元一次方程组、代数式求值、绝对值等知识点,灵活运用相关知识成为解题的关键.
17.
【分析】本题考查了实数的运算,熟练掌握运算法则是解题的关键.
分别求立方根,化简绝对值以及乘方运算,再进行加减计算.
【详解】解:
,
.
18.(1);(2)
【分析】本题主要考查了解二元一次方程组,解不等式组,掌握解方程组的方法和解一元一次不等式组的步骤是解题的关键.
(1)用加减消元法解二元一次方程组即可;
(2)先求出两个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集即可.
【详解】解:(1)
由得:,
解得:,
将代入①得:,
解得:,
∴原方程组的解为:;
(2)
由①得:,
由②得:,
∴原不等式组的解集为:.
19.
【分析】本题考查了对顶角相等,垂直的意义,解题关键是掌握上述知识,并能运用求解.
先利用垂直的意义,得出,再利用对顶角相等,求得的度数.
【详解】解:∵,
,
∵直线和相交于点,,
∴
.
20.(1)图见解析,点的坐标为
(2)5
【分析】本题考查平面直角坐标系,平移,利用网格求三角形的面积:
(1)根据平移前后坐标判断平移方式为:向下移动1个单位长度,再向左移动3个单位长度,由此确定点C的位置,即可求解;
(2)利用割补法求解.
【详解】(1)解:如图,即为所求,点的坐标为;
(2)解:如图,.
21.(1)100,15
(2)
(3)图见解析
(4)100
【分析】本题考查条形统计图与扇形统计图的综合应用,利用样本估计总体等,能够从图中获取相关信息是解题的关键.
(1)用D等级的人数及所占百分数可求总人数,总人数乘以A所占百分数,可求的值;
(2)用B等级所占比例乘以360度可得对应的圆心角的度数;
(3)先求出C等级人数,再补全条形统计图;
(4)利用样本估计总体即可.
【详解】(1)解:抽取学生总数为:(名),
,
故答案为:100,15;
(2)解:,
故答案为:;
(3)解:C等级人数为:,
补全条形统计图如下:
(4)解:,
答:估计学校应该准备100份奖品.
22.;两直线平行,同位角相等;;;同位角相等,两直线平行
【分析】本题考查平行线的判定和性质,根据平行线的判定定理和性质定理,角平分线的定义,结合已知过程,逐步推导论证即可.
【详解】证明:(已知).
(两直线平行,同位角相等).
平分(已知)
(角平分线的定义),
同理.
(等式的性质).
(同位角相等,两直线平行).
故答案为:;两直线平行,同位角相等;;;同位角相等,两直线平行.
23.(1)购买A型新能源公交车每辆需要60万元,购买B型新能源公交车每辆需要80万元
(2)购买5辆A型新能源公交车辆、15辆B型新能源公交车辆花钱最少
【分析】本题考查二元一次方程组的应用,一元一次不等式的应用,一次函数的应用:
(1)根据题意列二元一次方程组,解方程组即可;
(2)设购买A型新能源公交车m辆,则购买型新能源公交车辆,根据两者数量关系列不等式求出m的取值范围,再列出总费用W关于m的一次函数,根据函数增减性即可求解.
【详解】(1)解:设购买A型新能源公交车每辆需要x万元,购买B型新能源公交车每辆需要y万元,
根据题意,得
解得:,
答:购买A型新能源公交车每辆需要60万元,购买B型新能源公交车每辆需要80万元.
(2)解: 设购买A型新能源公交车m辆,则购买型新能源公交车辆,
根据题意,得,
解得,
设投入的费用为W万元,
则,
,
W随m的增大而减小,
当时W的值最小,(辆)
(万元),
即购买5辆A型新能源公交车辆、15辆B型新能源公交车辆花钱最少.
24.(1)
(2),理由见解析
【分析】本题主要考查了折叠的性质,平行线的判定及性质,熟练掌握平行线的判定及性质是解题的关键,
(1)根据平行线的判定判断即可;
(2)连接.由正方形可知,,进而得.由,得,从而可得.
【详解】(1)解:.理由如下:
由折叠可得,,
∴,
∴,
∴
(2)解:.
理由如下:如图,连接.
由正方形可知,,
∴.
∵,
∴,
∴,即.
25.(1)
(2)或3
(3)或
【分析】1)根据立方根定义求出a的值,根据非负数的性质求出b、c的值,即可得出答案;
(2)先求出,再求出面积小的那个部分为,共有两种情况分别画出图形,求出结果即可;
(3)先求出平移后点A的坐标为,,连接,过点A作轴于点M,过点B作轴,求出,再求出,分两种情况:当点G在下方时,当点G在上方时,求出结果即可.
【详解】(1)解:∵是的立方根,且满足,
∴,,,
解得:,,
∴;
故答案为:;
(2)解:∵,
∴,
∵要将面积分为两个部分,
∴面积小的那个部分为,
共有两种情况:
①如图1,设与y轴交于点,平移后点坐标分别为,,
则,,连接,
,即,
解得:,
,
,
开平方得:,
解得:或,
∵,
∴;
如图2,设与轴交于点,平移后点坐标分别为,,,则,连接.
同理:,
即,
解得:,
,
开平方得:,
解得:或9,
∵当时,三角形都在轴左侧,不符合题意,
;
综上所述,或3;
(3)解:根据平移可知,平移后点A的坐标为,,
连接,过点A作轴于点M,过点B作轴,如图所示:
设与y轴交于点P,设,
则,
∵,
∴,
解得:,
∴;
∵,,,,,,
∴
,
当点G在下方时,如图所示:
,
∵,
∴,
解得:;
当点G在上方时,如图所示:
,
∵,
∴,
解得:;
综上分析可知:点纵坐标为或.
【点睛】本题主要考查了算术平方根的非负性,坐标与平移,三角形面积计算,解题的关键是数形结合,注意进行分类讨论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合试题 2024-2025学年下期初中
数学人教版七年级下册(新教材)
一、单选题
1.在实数,,,,,,(两个1之间依次多一个6)中,无理数的个数是( )
A.5 B.4 C.3 D.2
2.化简的结果是( )
A.3 B. C. D.9
3.以下调查中,适合全面调查的是( )
A.了解山西中学生的视力情况
B.检测临汾地区和运城地区的城市空气质量
C.调查汾河源头现有鱼的数量
D.调查某教研组老师是否参加新教材培训
4.如图,直线与交于点O,,若,则的度数为( )
A. B. C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.我国古代数学著作《算法统宗》中记载了这样一道题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?其大意为:用绳子测量井的深度,如果将绳子折成三等份,则一份绳长比井深多4尺,如果将绳子折成四等份,则一份绳长比井深多1尺,则绳长、井深各是多少尺?若设绳长x尺,井深y尺,则下列所列方程组正确的是( )
A. B. C. D.
7.如果关于的不等式的解集为,那么的取值范围是( )
A. B. C. D.
8.点P在第二象限内,点P到x轴的距离是6,到y轴的距离是2,那么点P的坐标为( )
A.(﹣6,2) B.(﹣2,﹣6) C.(﹣2,6) D.(2,﹣6)
9.如图,智能机器人从平面直角坐标系的原点O出发,向上走1个单位长度到达点,再向左走1个单位长度到达点,再向下走2个单位长度到达点,再向右走2个单位长度到达点,再向上走3个单位长度到达点,…以此规律走下去,当智能机器人到达点时,它的坐标为( )
A. B. C. D.
10.已知关于,的二元一次方程组给出下列结论中正确的是( )
①当时,方程组的解也是方程的解;
②无论取什么实数,的值始终不变;
③当时,.
A.①② B.①③ C.②③ D.①②③
二、填空题
11.计算:= .
12.在平面直角坐标系中,若将点先向上平移3个单位长度,再向右平移3个单位长度得到点,则点的坐标为 .
13.统计得到的一组数据最大值为139,最小值为48,取组距为10,可分成 组.
14.已知关于的方程组,若其解互为相反数,则的值为 .
15.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190”为一次操作.若操作恰好进行两次停止,则x的取值范围是 .
16.下列命题:①相等的角是对顶角;②算术平方根等于它本身的数有两个,分别是0和1;③已知关于的二元一次方程组,不论取什么有理数,的值始终不变;④已知正实数的平方根是和,若,则;⑤若不等式对一切实数都成立,则的最大值是5;
其中真命题是: .(请填序号)
三、解答题
17.计算:.
18.(1)解方程组:
(2)解不等式组:
19.如图,直线和相交于点,,若,求的度数.
20.在平面直角坐标系中,已知点,,现将线段按照某种方式进行平移,使点平移到点处,点平移到点处.
(1)画出平移后的线段,并写出点的坐标;
(2)连接,,求三角形的面积.
21.2025年六五环境日的主题为“美丽中国我先行”,旨在深入学习宣传贯彻习近平生态文明思想,展示全国各地推进美丽中国先行区建设的实践成果并倡议社会公众积极行动,投身美丽中国建设.某学校组织七年级学生开展生态环境知识竞赛,随机抽取了一部分学生的成绩进行统计分析,把分数(满分为100分,成绩均不低于60分)分成四个等级(.,.,.,..)并绘制了不完整的条形图与扇形图.
请根据以上信息,解答下列问题:
(1)本次共抽取________名学生,的值为________;
(2)在扇形统计图中,表示等级的扇形圆心角的度数为________;
(3)根据已有信息,把条形图补全;
(4)该校七年级学生有500人,该校计划为七年级生态环境知识竞赛成绩为“优秀”的学生颁发奖品,估计学校应该准备多少份奖品?
22.小华在探究“两直线平行,一组同位角的角平分线互相平行”时,画出图形,并写出如下不完整的证明过程.请你补充完整.
已知:如图,,与,分别相交于点,,平分,平分.
求证:.
证明:(已知).
________(________).
平分(已知)
________(角平分线的定义),
同理.
________(等式的性质).
(________).
23.国家主席习近平在2025年新年贺词中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.“今年某市计划引进,两种车型的新能源公交车,若购买型公交车2辆,型公交车3辆,共需360万元;若购买型公交车3辆,型公交车2辆,共需340万元
(1)求购买型和型新能源公交车每辆分别需要多少万元?
(2)若计划本批次购买型和型新能源公交车20辆,要求两种车型都要购买,且型新能源公交车的数量不超过型新能源公交车数量的,请写出花钱最少的购车方案.
24.【综合实践】——折纸中的数学
某兴趣小组在探究“过直线外一点作已知直线的平行线”的活动中,通过以下的折纸方式找符合要求的直线.如图①,在一张正方形纸片的两边上分别有,两点,连接,是正方形纸片上一点,用折纸的方法过点作的平行线的基本步骤如下:
第一步:如图②,过点进行第一次折叠,使点的对应点落在上,折痕与互相垂直,垂足为,打开纸张铺平;
第二步:如图③,过点进行第二次折叠,使折痕,打开纸张铺平(如图④).
(1)根据上述步骤可知,与的位置关系是________.
(2)如图④,设直线与正方形上、下两边分别交于点,,试探究与的数量关系,并说明理由.
25.如图,在平面直角坐标系中,已知点,,,其中是的立方根,且满足.
(1)直接写出、、三点坐标:___________,___________,___________;
(2)如图1,将三角形向左平移个单位,三角形被轴分成面积比为的两个部分,求的值.
(3)如图2,将线段向上平移2个单位长度,点为轴上一动点,点为第一象限内动点,且,连接,若,直接写出点的纵坐标(用含的式子表示).
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B B C A C A D
1.C
【分析】本题考查了无理数的定义,掌握无理数的常见形式“①最终结果含有开方开不尽的数,②最终结果含有的数,③形如(每两个增加一个).”是解题的关键.
【详解】解:是有限小数,0,3是整数,是分数,它们不是无理数;
,,(两个1之间依次多一个6)是无限不循环小数,它们是无理数,共3个;
故选:C.
2.A
【分析】本题考查算术平方根计算.根据题意先将根式中计算出来,再开根号即可得到本题答案.
【详解】解:,
故选:A.
3.D
【分析】根据抽样调查和全面调查的特点,选择合适的调查方式.本题考查了调查的两种方式,熟练掌握两种方式使用的基本特点是解题的关键.
【详解】解:了解山西中学生的视力情况,采用抽样调查方式,
∴A不符合题意;
检测临汾地区和运城地区的城市空气质量,采用抽样调查方式,
∴B不符合题意;
调查汾河源头现有鱼的数量,采用抽查方式,
∴C不符合题意;
调查某教研组老师是否参加新教材培训,采取全面调查的方式,
∴D符合题意;
故选:D.
4.B
【分析】直接利用邻补角的定义结合垂线的定义进而得出答案.
【详解】解:∵,
∴,
∵,
∴,
∴,故B正确.
故选:B.
【点睛】主要考查了邻补角和垂线的定义,正确得出的度数是解题关键.
5.B
【分析】本题主要考查了在数轴上表示不等式的解集,大于号,要向数轴右边画,且表示的点画空心圆圈,据此可得答案.
【详解】解:大于,则应从表示的点向右画,并且不包含的点,即表示的点画空心圆圈,即数轴表示如下:
故选:B.
6.C
【分析】本题主要考查了二元一次方程组的实际应用,设绳长x尺,井深y尺,根据将绳子折成三等份,则一份绳长比井深多4尺可得方程,根据将绳子折成四等份,则一份绳长比井深多1尺可得方程,据此列出方程组即可.
【详解】解:由题意得,,
故选:C.
7.A
【分析】利用不等式的基本性质求解即可.
【详解】解:∵不等式的解集为,
∴,
故选:A.
【点睛】本题考查不等式的基本性质、不等式的解集,熟练掌握不等式的基本性质的运用,注意符号的变化是解答的关键.
8.C
【分析】根据点(x,y)到x轴的距离为|y|,到y轴的距离|x|解答即可.
【详解】解:设点P坐标为(x,y),
∵点P到x轴的距离是6,到y轴的距离是2,
∴|y|=6,|x|=2,
∵点P在第二象限内,
∴y=6,x=-2,
∴点P坐标为(-2,6),
故选:C.
【点睛】本题考查点到坐标轴的距离、点所在的象限,熟知点到坐标轴的距离与坐标的关系是解答的关键.
9.A
【分析】本题主要考查坐标与图形变化-平移和找规律的知识点,熟悉平移规律和坐标系是解答本题的关键.
根据这些点的坐标找出某一象限点的坐标规律,最后判断所在象限,从而求出其坐标.
【详解】解:依题意可知:点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,点的坐标为,且,
∴是第一象限的点,
∴的坐标是.
故选:A.
10.D
【分析】本题考查了含参二元一次方程组中参数的确定,二元一次方程组的解法,解一元一次不等式等知识,掌握二元一次方程组的解法是解题的关键.
解方程组得到,再逐项进行判断即可.
【详解】解:解方程组,得,
当时,,,代入得到,满足方程,结论①正确;
,与无关,始终为定值3,结论②正确;
若,即,解得:,
所以当时,成立,结论③正确;
综上,①②③均正确,
故选:D.
11.2
【分析】根据立方根的定义进行计算.
【详解】解:∵23=8,
∴,
故答案为:2.
12.
【分析】此题主要考查坐标与图形变化-平移,掌握点的坐标变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.利用点平移的坐标规律,把点的横坐标加3,纵坐标加3即可得到点的坐标.
【详解】解:∵将点先向上平移3个单位长度,再向右平移3个单位长度得到点,
∴点的坐标是,即.
故答案为:.
13.10
【分析】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数(最大值最小值)÷组距计算,注意小数部分要进位.
【详解】解:∵极差为,
∴由,
所以可分10组,
故答案为:10.
14.2
【分析】本题考查根据方程组的解的情况求参数,两个方程相减,结合互为相反数的两数之和为0,列出关于的一元一次方程,进行求解即可.
【详解】解:,
,得:,
∵互为相反数,
∴,
∴;
故答案为:2.
15./
【分析】根据第一次操作没有停止可得不等式,根据第二次操作后停止可得不等式,由此建立不等式组求解即可.
【详解】解:由题意得,,
解得,
故答案为:.
【点睛】本题主要考查了解一元一次不等式组,正确理解题意列出不等式组是解题的关键.
16.②③④
【分析】根据对顶角、平方根、解二元一次方程组、代数式求值、绝对值等知识逐项判断即可.
【详解】解:①对顶角一定相等,但相等的角不一定是对顶角,所以①是假命题;
②算术平方根等于它本身的数有两个,分别是0和1,即②是真命题.
③解方程组可得:,则,
所以不论取什么有理数,的值始终不变,③是真命题.
④因为正实数的平方根是和,
所以,即,且,
因为,
所以,即,
因为正实数,则,④是真命题.
⑤:设,
当时,;
当时,;
当时,.
所以的最小值是3,
若不等式对一切实数a都成立,则,即m的最大值是3,则⑤是假命题.
故答案为:②③④.
【点睛】本题主要考查了对顶角、平方根、解二元一次方程组、代数式求值、绝对值等知识点,灵活运用相关知识成为解题的关键.
17.
【分析】本题考查了实数的运算,熟练掌握运算法则是解题的关键.
分别求立方根,化简绝对值以及乘方运算,再进行加减计算.
【详解】解:
,
.
18.(1);(2)
【分析】本题主要考查了解二元一次方程组,解不等式组,掌握解方程组的方法和解一元一次不等式组的步骤是解题的关键.
(1)用加减消元法解二元一次方程组即可;
(2)先求出两个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集即可.
【详解】解:(1)
由得:,
解得:,
将代入①得:,
解得:,
∴原方程组的解为:;
(2)
由①得:,
由②得:,
∴原不等式组的解集为:.
19.
【分析】本题考查了对顶角相等,垂直的意义,解题关键是掌握上述知识,并能运用求解.
先利用垂直的意义,得出,再利用对顶角相等,求得的度数.
【详解】解:∵,
,
∵直线和相交于点,,
∴
.
20.(1)图见解析,点的坐标为
(2)5
【分析】本题考查平面直角坐标系,平移,利用网格求三角形的面积:
(1)根据平移前后坐标判断平移方式为:向下移动1个单位长度,再向左移动3个单位长度,由此确定点C的位置,即可求解;
(2)利用割补法求解.
【详解】(1)解:如图,即为所求,点的坐标为;
(2)解:如图,.
21.(1)100,15
(2)
(3)图见解析
(4)100
【分析】本题考查条形统计图与扇形统计图的综合应用,利用样本估计总体等,能够从图中获取相关信息是解题的关键.
(1)用D等级的人数及所占百分数可求总人数,总人数乘以A所占百分数,可求的值;
(2)用B等级所占比例乘以360度可得对应的圆心角的度数;
(3)先求出C等级人数,再补全条形统计图;
(4)利用样本估计总体即可.
【详解】(1)解:抽取学生总数为:(名),
,
故答案为:100,15;
(2)解:,
故答案为:;
(3)解:C等级人数为:,
补全条形统计图如下:
(4)解:,
答:估计学校应该准备100份奖品.
22.;两直线平行,同位角相等;;;同位角相等,两直线平行
【分析】本题考查平行线的判定和性质,根据平行线的判定定理和性质定理,角平分线的定义,结合已知过程,逐步推导论证即可.
【详解】证明:(已知).
(两直线平行,同位角相等).
平分(已知)
(角平分线的定义),
同理.
(等式的性质).
(同位角相等,两直线平行).
故答案为:;两直线平行,同位角相等;;;同位角相等,两直线平行.
23.(1)购买A型新能源公交车每辆需要60万元,购买B型新能源公交车每辆需要80万元
(2)购买5辆A型新能源公交车辆、15辆B型新能源公交车辆花钱最少
【分析】本题考查二元一次方程组的应用,一元一次不等式的应用,一次函数的应用:
(1)根据题意列二元一次方程组,解方程组即可;
(2)设购买A型新能源公交车m辆,则购买型新能源公交车辆,根据两者数量关系列不等式求出m的取值范围,再列出总费用W关于m的一次函数,根据函数增减性即可求解.
【详解】(1)解:设购买A型新能源公交车每辆需要x万元,购买B型新能源公交车每辆需要y万元,
根据题意,得
解得:,
答:购买A型新能源公交车每辆需要60万元,购买B型新能源公交车每辆需要80万元.
(2)解: 设购买A型新能源公交车m辆,则购买型新能源公交车辆,
根据题意,得,
解得,
设投入的费用为W万元,
则,
,
W随m的增大而减小,
当时W的值最小,(辆)
(万元),
即购买5辆A型新能源公交车辆、15辆B型新能源公交车辆花钱最少.
24.(1)
(2),理由见解析
【分析】本题主要考查了折叠的性质,平行线的判定及性质,熟练掌握平行线的判定及性质是解题的关键,
(1)根据平行线的判定判断即可;
(2)连接.由正方形可知,,进而得.由,得,从而可得.
【详解】(1)解:.理由如下:
由折叠可得,,
∴,
∴,
∴
(2)解:.
理由如下:如图,连接.
由正方形可知,,
∴.
∵,
∴,
∴,即.
25.(1)
(2)或3
(3)或
【分析】1)根据立方根定义求出a的值,根据非负数的性质求出b、c的值,即可得出答案;
(2)先求出,再求出面积小的那个部分为,共有两种情况分别画出图形,求出结果即可;
(3)先求出平移后点A的坐标为,,连接,过点A作轴于点M,过点B作轴,求出,再求出,分两种情况:当点G在下方时,当点G在上方时,求出结果即可.
【详解】(1)解:∵是的立方根,且满足,
∴,,,
解得:,,
∴;
故答案为:;
(2)解:∵,
∴,
∵要将面积分为两个部分,
∴面积小的那个部分为,
共有两种情况:
①如图1,设与y轴交于点,平移后点坐标分别为,,
则,,连接,
,即,
解得:,
,
,
开平方得:,
解得:或,
∵,
∴;
如图2,设与轴交于点,平移后点坐标分别为,,,则,连接.
同理:,
即,
解得:,
,
开平方得:,
解得:或9,
∵当时,三角形都在轴左侧,不符合题意,
;
综上所述,或3;
(3)解:根据平移可知,平移后点A的坐标为,,
连接,过点A作轴于点M,过点B作轴,如图所示:
设与y轴交于点P,设,
则,
∵,
∴,
解得:,
∴;
∵,,,,,,
∴
,
当点G在下方时,如图所示:
,
∵,
∴,
解得:;
当点G在上方时,如图所示:
,
∵,
∴,
解得:;
综上分析可知:点纵坐标为或.
【点睛】本题主要考查了算术平方根的非负性,坐标与平移,三角形面积计算,解题的关键是数形结合,注意进行分类讨论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
