2.4.3 向量与夹角 学案(含答案)
文档属性
| 名称 | 2.4.3 向量与夹角 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 17:28:34 | ||
图片预览



文档简介
2.4.3 向量与夹角
(1)理解直线与直线、直线与平面、平面与平面的夹角定义.(2)能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.
新知初探·课前预习——突出基础性
教 材 要 点
要点一 异面直线所成的角
设两条异面直线l1与l2所成的角为θ(θ∈(0,]),它们的方向向量分别为v1,v2,则cos θ=|cos 〈v1,v2〉|=.
要点二 直线与平面所成的角
直线l与平面α所成的角为θ,v是直线l的一个方向向量,n是平面α的一个法向量,则sin θ=|cos 〈v,n〉|=.
要点三 平面与平面所成的角
设两个平面α1和α2所成的角为θ,平面α1,α2的法向量分别为n1,n2,则cos θ=|cos 〈n1,n2〉|=.
批注 异面直线所成的角为锐角或直角,而不共线的向量的夹角为(0,π),所以计算公式中要加绝对值.
批注 直线与平面所成角的范围为[0,],而向量之间的夹角的范围为[0,π],所以计算公式中要加绝对值.
批注 利用公式求二面角的平面角时,要注意〉与二面角大小的关系,是相等还是互补,需要结合图形进行判断
基 础 自 测
1.判断正误(正确的画“√”,错误的画“×”)
(1)两条异面直线所成的角与两直线的方向向量所成的角相等.( )
(2)直线与平面所成的角等于直线与该平面法向量夹角的余角.( )
(3)二面角的大小就是该二面角两个面的法向量的夹角.( )
2.设直线l1的方向向量为s1=(1,1,1),直线l2的方向向量为s2=(-2,2,-2),则l1,l2夹角的余弦值为( )
A.- B. C. D.
3.已知两平面的法向量分别为n1=(0,1,0),n2=(0,-1,1),则两平面所成的锐二面角的大小为( )
A.30° B.45°
C.60° D.75°
4.若直线l的方向向量为v=(1,0,3),平面α的一个法向量为n=(-2,0,2),则直线l与平面α所成角的正弦值为________.
题型探究·课堂解透——强化创新性
题型1 向量法求两异面直线所成角
例1 如图所示,在三棱柱ABC A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
方法归纳
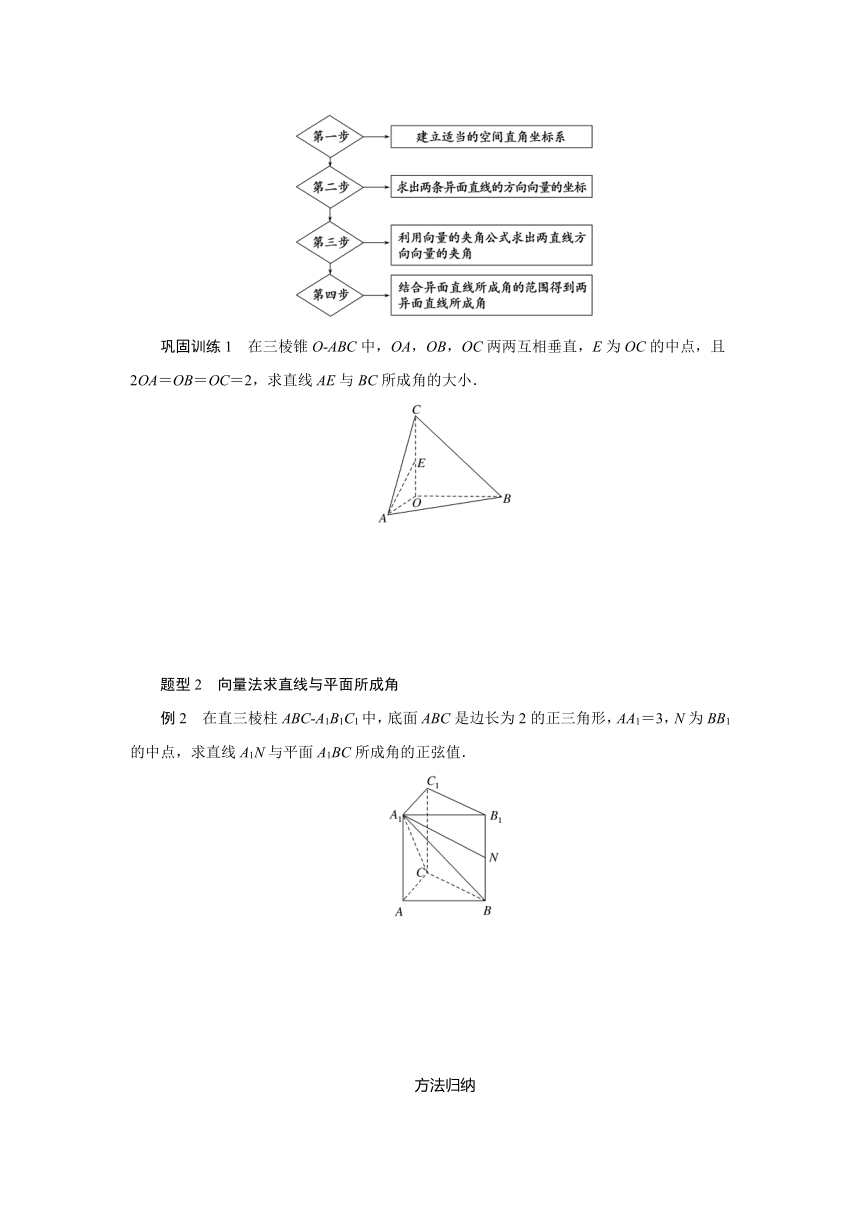
利用坐标法求两异面直线所成角的步骤
巩固训练1 在三棱锥O ABC中,OA,OB,OC两两互相垂直,E为OC的中点,且2OA=OB=OC=2,求直线AE与BC所成角的大小.
题型2 向量法求直线与平面所成角
例2 在直三棱柱ABC A1B1C1中,底面ABC是边长为2的正三角形,AA1=3,N为BB1的中点,求直线A1N与平面A1BC所成角的正弦值.
方法归纳
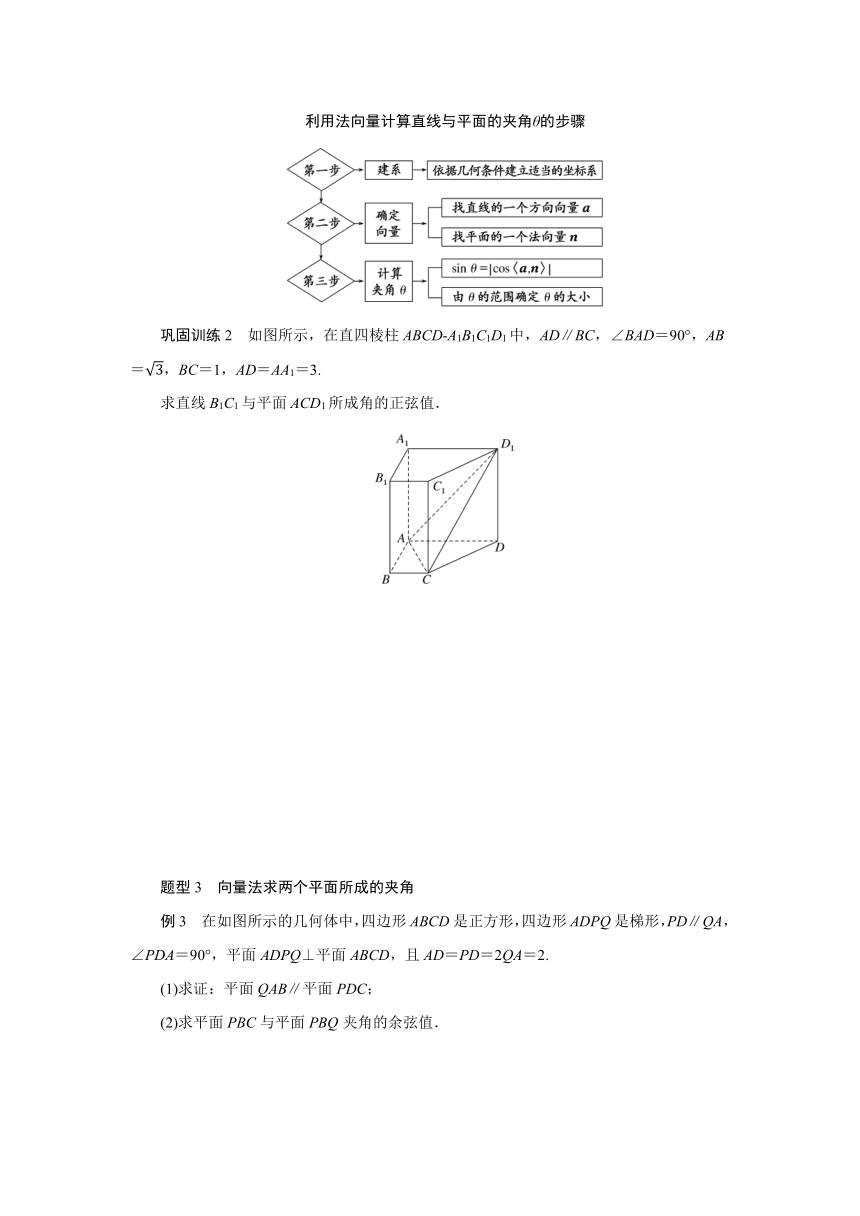
利用法向量计算直线与平面的夹角θ的步骤
巩固训练2 如图所示,在直四棱柱ABCD A1B1C1D1中,AD∥BC,∠BAD=90°,AB=,BC=1,AD=AA1=3.
求直线B1C1与平面ACD1所成角的正弦值.
题型3 向量法求两个平面所成的夹角
例3 在如图所示的几何体中,四边形ABCD是正方形,四边形ADPQ是梯形,PD∥QA,∠PDA=90°,平面ADPQ⊥平面ABCD,且AD=PD=2QA=2.
(1)求证:平面QAB∥平面PDC;
(2)求平面PBC与平面PBQ夹角的余弦值.
方法归纳
利用法向量求两个平面夹角的步骤
巩固训练3 在四棱锥P ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,BC∥AD,AD⊥AB,E,F分别是棱AB,PC的中点.
(1)证明:EF∥平面PAD;
(2)若PA=AB=BC,AD=2BC,求平面AEF与平面CDF夹角的余弦值.
2.4.3 向量与夹角
新知初探·课前预习
[基础自测]
1.(1)× (2)× (3)×
2.解析:∵cos 〈s1,s2〉==-,
∴l1,l2夹角的余弦值为.
答案:B
3.解析:cos 〈n1,n2〉===-,所以两平面所成的锐二面角的大小为45°.
答案:B
4.解析:设v=(1,0,3)与n=(-2,0,2)的夹角为θ,直线l与平面α所成角为φ,
所以sin φ=|cos θ|=
==.
答案:
题型探究·课堂解透
例1解析:分别以直线BC,BA,B1B为x,y,z轴,建立空间直角坐标系(如图).
设AB=1,则B(0,0,0),E(0,,0),F(0,0,),C1(1,0,1),
所以==(1,0,1),
于是,〉===,
所以直线EF和BC1所成角的大小为60°.
巩固训练1
解析:由已知以O为原点,以的方向为x,y,z轴建立空间直角坐标系,
由2OA=OB=OC=2,知A(1,0,0),E(0,0,1),B(0,2,0),C(0,0,2),
所以=(-1,0,1),=(0,-2,2),
所以|cos 〈〉|=
==,
所以〈〉=,即直线AE与BC所成角的大小为.
例2 解析:取AB中点O,A1B1中点O1,连接OC,OO1.
∵△ABC是边长为2的正三角形,∴OC⊥AB.
以OB,OC,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系O xyz
则C(0,,0),A1(-1,0,3),B(1,0,0),N(1,0,),
==(-2,0,3),=(2,0,-),
设平面A1BC的法向量n=(x,y,z),
由,得,取n=(3,,2),
设直线A1N与平面A1BC所成的角为θ,则
sin θ=|cos 〈n,A1N〉|===,
∴直线A1N与平面A1BC所成角的正弦值为.
巩固训练2
解析:以A为原点,以的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,
则A(0,0,0),C(,1,0),B1(,0,3),D(0,3,0),C1(,1,3),D1(0,3,3).
设平面ACD1的法向量为m=(x,y,z),
==(0,3,3),
则即
令x=1,则y=-,z=,
∴平面ACD1的一个法向量为m=(1,-).
设直线B1C1与平面ACD1所成的角为=(0,1,0),∴sin θ==,
∴直线B1C1与平面ACD1所成角的正弦值为.
例3 解析:(1)证明:四边形ABCD是正方形,可得AB∥CD,
又AB 平面DCP,CD 平面DCP,
则有AB∥平面DCP,
四边形ADPQ是梯形,可得QA∥PD,
又QA 平面DCP,PD 平面DCP,
则有QA∥平面DCP,
又QA=A,
故平面QAB∥平面PDC.
(2)依题意知DA,DC,DP两两垂直,故以D为原点,DA,DC,DP所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系. 则有
C(0,2,0),P(0,0,2),B(2,2,0),Q(2,0,1)
可得=(2,2,-2),=(0,2,-2),=(2,0,-1),
设平面PBC的一个法向量n=(x,y,z),则有:
,
取y=1,可得n=(0,1,1),
设平面PBQ的一个法向量m=(x,y,z),则有
,
取x=1,可得m=(1,1,2),
设平面PBC与平面PBQ的夹角为θ,则cos θ===,
故平面PBC与平面PBQ夹角的余弦值为.
巩固训练3 解析:(1)证明:取CD的中点G,连接EG,FG.
因为F,G分别是棱PC,CD的中点,所以FG∥PD,
又FG 平面PAD,PD 平面PAD,所以FG∥平面PAD.
因为BC∥AD,且E,G分别是棱AB,CD的中点,所以EG∥AD,
又EG 平面PAD,AD 平面PAD,所以EG∥平面PAD.
因为EG,FG 平面EFG,且EG=G,所以平面EFG∥平面PAD.
因为EF 平面EFG,所以EF∥平面PAD.
(2)以A为原点,分别以的方向为x,y,z轴的正方向,建立空间直角坐标系,
设AB=2,则A(0,0,0),C(2,2,0),D(0,4,0),E(1,0,0),P(0,0,2).
因为F是棱PC的中点,所以F(1,1,1),
所以=(1,0,0),=(1,1,1),=(-2,2,0),=(-1,-1,1).
设平面AEF的法向量为n=(x1,y1,z1),
则,令y1=1,得n=(0,1,-1).
设平面CDF的法向量为m=(x2,y2,z2),
则令x2=1,得m=(1,1,2).
设平面AEF与平面CDF的夹角为θ,则cos θ=|cos 〈m,n〉|===.
所以平面AEF与平面CDF夹角的余弦值为.
(1)理解直线与直线、直线与平面、平面与平面的夹角定义.(2)能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.
新知初探·课前预习——突出基础性
教 材 要 点
要点一 异面直线所成的角
设两条异面直线l1与l2所成的角为θ(θ∈(0,]),它们的方向向量分别为v1,v2,则cos θ=|cos 〈v1,v2〉|=.
要点二 直线与平面所成的角
直线l与平面α所成的角为θ,v是直线l的一个方向向量,n是平面α的一个法向量,则sin θ=|cos 〈v,n〉|=.
要点三 平面与平面所成的角
设两个平面α1和α2所成的角为θ,平面α1,α2的法向量分别为n1,n2,则cos θ=|cos 〈n1,n2〉|=.
批注 异面直线所成的角为锐角或直角,而不共线的向量的夹角为(0,π),所以计算公式中要加绝对值.
批注 直线与平面所成角的范围为[0,],而向量之间的夹角的范围为[0,π],所以计算公式中要加绝对值.
批注 利用公式求二面角的平面角时,要注意〉与二面角大小的关系,是相等还是互补,需要结合图形进行判断
基 础 自 测
1.判断正误(正确的画“√”,错误的画“×”)
(1)两条异面直线所成的角与两直线的方向向量所成的角相等.( )
(2)直线与平面所成的角等于直线与该平面法向量夹角的余角.( )
(3)二面角的大小就是该二面角两个面的法向量的夹角.( )
2.设直线l1的方向向量为s1=(1,1,1),直线l2的方向向量为s2=(-2,2,-2),则l1,l2夹角的余弦值为( )
A.- B. C. D.
3.已知两平面的法向量分别为n1=(0,1,0),n2=(0,-1,1),则两平面所成的锐二面角的大小为( )
A.30° B.45°
C.60° D.75°
4.若直线l的方向向量为v=(1,0,3),平面α的一个法向量为n=(-2,0,2),则直线l与平面α所成角的正弦值为________.
题型探究·课堂解透——强化创新性
题型1 向量法求两异面直线所成角
例1 如图所示,在三棱柱ABC A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,试求直线EF和BC1所成的角.
方法归纳
利用坐标法求两异面直线所成角的步骤
巩固训练1 在三棱锥O ABC中,OA,OB,OC两两互相垂直,E为OC的中点,且2OA=OB=OC=2,求直线AE与BC所成角的大小.
题型2 向量法求直线与平面所成角
例2 在直三棱柱ABC A1B1C1中,底面ABC是边长为2的正三角形,AA1=3,N为BB1的中点,求直线A1N与平面A1BC所成角的正弦值.
方法归纳
利用法向量计算直线与平面的夹角θ的步骤
巩固训练2 如图所示,在直四棱柱ABCD A1B1C1D1中,AD∥BC,∠BAD=90°,AB=,BC=1,AD=AA1=3.
求直线B1C1与平面ACD1所成角的正弦值.
题型3 向量法求两个平面所成的夹角
例3 在如图所示的几何体中,四边形ABCD是正方形,四边形ADPQ是梯形,PD∥QA,∠PDA=90°,平面ADPQ⊥平面ABCD,且AD=PD=2QA=2.
(1)求证:平面QAB∥平面PDC;
(2)求平面PBC与平面PBQ夹角的余弦值.
方法归纳
利用法向量求两个平面夹角的步骤
巩固训练3 在四棱锥P ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,BC∥AD,AD⊥AB,E,F分别是棱AB,PC的中点.
(1)证明:EF∥平面PAD;
(2)若PA=AB=BC,AD=2BC,求平面AEF与平面CDF夹角的余弦值.
2.4.3 向量与夹角
新知初探·课前预习
[基础自测]
1.(1)× (2)× (3)×
2.解析:∵cos 〈s1,s2〉==-,
∴l1,l2夹角的余弦值为.
答案:B
3.解析:cos 〈n1,n2〉===-,所以两平面所成的锐二面角的大小为45°.
答案:B
4.解析:设v=(1,0,3)与n=(-2,0,2)的夹角为θ,直线l与平面α所成角为φ,
所以sin φ=|cos θ|=
==.
答案:
题型探究·课堂解透
例1解析:分别以直线BC,BA,B1B为x,y,z轴,建立空间直角坐标系(如图).
设AB=1,则B(0,0,0),E(0,,0),F(0,0,),C1(1,0,1),
所以==(1,0,1),
于是,〉===,
所以直线EF和BC1所成角的大小为60°.
巩固训练1
解析:由已知以O为原点,以的方向为x,y,z轴建立空间直角坐标系,
由2OA=OB=OC=2,知A(1,0,0),E(0,0,1),B(0,2,0),C(0,0,2),
所以=(-1,0,1),=(0,-2,2),
所以|cos 〈〉|=
==,
所以〈〉=,即直线AE与BC所成角的大小为.
例2 解析:取AB中点O,A1B1中点O1,连接OC,OO1.
∵△ABC是边长为2的正三角形,∴OC⊥AB.
以OB,OC,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系O xyz
则C(0,,0),A1(-1,0,3),B(1,0,0),N(1,0,),
==(-2,0,3),=(2,0,-),
设平面A1BC的法向量n=(x,y,z),
由,得,取n=(3,,2),
设直线A1N与平面A1BC所成的角为θ,则
sin θ=|cos 〈n,A1N〉|===,
∴直线A1N与平面A1BC所成角的正弦值为.
巩固训练2
解析:以A为原点,以的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,
则A(0,0,0),C(,1,0),B1(,0,3),D(0,3,0),C1(,1,3),D1(0,3,3).
设平面ACD1的法向量为m=(x,y,z),
==(0,3,3),
则即
令x=1,则y=-,z=,
∴平面ACD1的一个法向量为m=(1,-).
设直线B1C1与平面ACD1所成的角为=(0,1,0),∴sin θ==,
∴直线B1C1与平面ACD1所成角的正弦值为.
例3 解析:(1)证明:四边形ABCD是正方形,可得AB∥CD,
又AB 平面DCP,CD 平面DCP,
则有AB∥平面DCP,
四边形ADPQ是梯形,可得QA∥PD,
又QA 平面DCP,PD 平面DCP,
则有QA∥平面DCP,
又QA=A,
故平面QAB∥平面PDC.
(2)依题意知DA,DC,DP两两垂直,故以D为原点,DA,DC,DP所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系. 则有
C(0,2,0),P(0,0,2),B(2,2,0),Q(2,0,1)
可得=(2,2,-2),=(0,2,-2),=(2,0,-1),
设平面PBC的一个法向量n=(x,y,z),则有:
,
取y=1,可得n=(0,1,1),
设平面PBQ的一个法向量m=(x,y,z),则有
,
取x=1,可得m=(1,1,2),
设平面PBC与平面PBQ的夹角为θ,则cos θ===,
故平面PBC与平面PBQ夹角的余弦值为.
巩固训练3 解析:(1)证明:取CD的中点G,连接EG,FG.
因为F,G分别是棱PC,CD的中点,所以FG∥PD,
又FG 平面PAD,PD 平面PAD,所以FG∥平面PAD.
因为BC∥AD,且E,G分别是棱AB,CD的中点,所以EG∥AD,
又EG 平面PAD,AD 平面PAD,所以EG∥平面PAD.
因为EG,FG 平面EFG,且EG=G,所以平面EFG∥平面PAD.
因为EF 平面EFG,所以EF∥平面PAD.
(2)以A为原点,分别以的方向为x,y,z轴的正方向,建立空间直角坐标系,
设AB=2,则A(0,0,0),C(2,2,0),D(0,4,0),E(1,0,0),P(0,0,2).
因为F是棱PC的中点,所以F(1,1,1),
所以=(1,0,0),=(1,1,1),=(-2,2,0),=(-1,-1,1).
设平面AEF的法向量为n=(x1,y1,z1),
则,令y1=1,得n=(0,1,-1).
设平面CDF的法向量为m=(x2,y2,z2),
则令x2=1,得m=(1,1,2).
设平面AEF与平面CDF的夹角为θ,则cos θ=|cos 〈m,n〉|===.
所以平面AEF与平面CDF夹角的余弦值为.
同课章节目录
