【开学摸底培优】专项05 操作题-2025年人教版数学四升五暑假开学摸底培优精练(含解析)
文档属性
| 名称 | 【开学摸底培优】专项05 操作题-2025年人教版数学四升五暑假开学摸底培优精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 20:50:46 | ||
图片预览

文档简介
2025年人教版数学四升五暑假开学摸底培优精练(人教版)
专项05 操作题
学校:___________姓名:___________班级:___________考号:___________
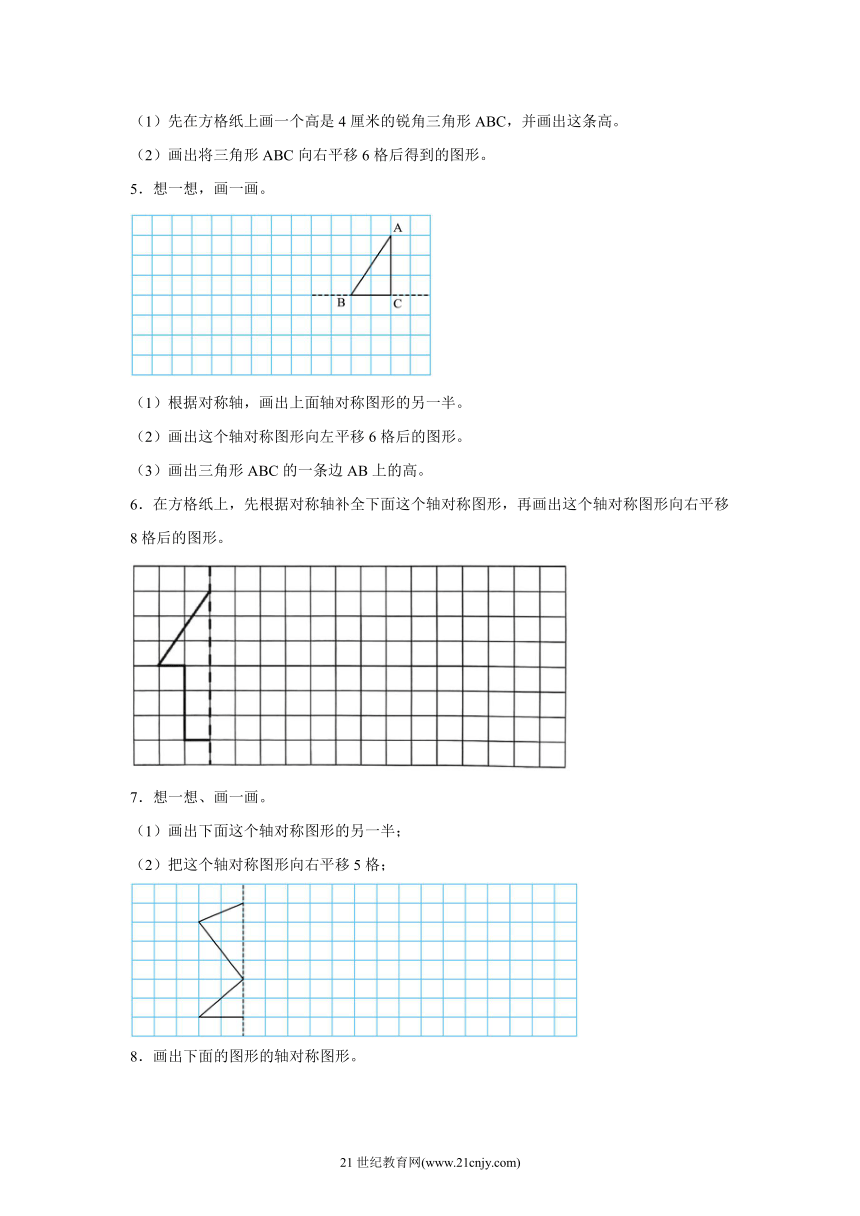
1.根据对称轴补全下面轴对称图形。
2.根据要求在方格纸上画图。
(1)根据对称轴补全下面这个轴对称图形。
(2)画出这个轴对称图形向右平移6个格后的图形。
3.画出下面三角形指定底边上的高,并标出“高”。
4.按要求在下面方格纸上画一画。
(1)先在方格纸上画一个高是4厘米的锐角三角形ABC,并画出这条高。
(2)画出将三角形ABC向右平移6格后得到的图形。
5.想一想,画一画。
(1)根据对称轴,画出上面轴对称图形的另一半。
(2)画出这个轴对称图形向左平移6格后的图形。
(3)画出三角形ABC的一条边AB上的高。
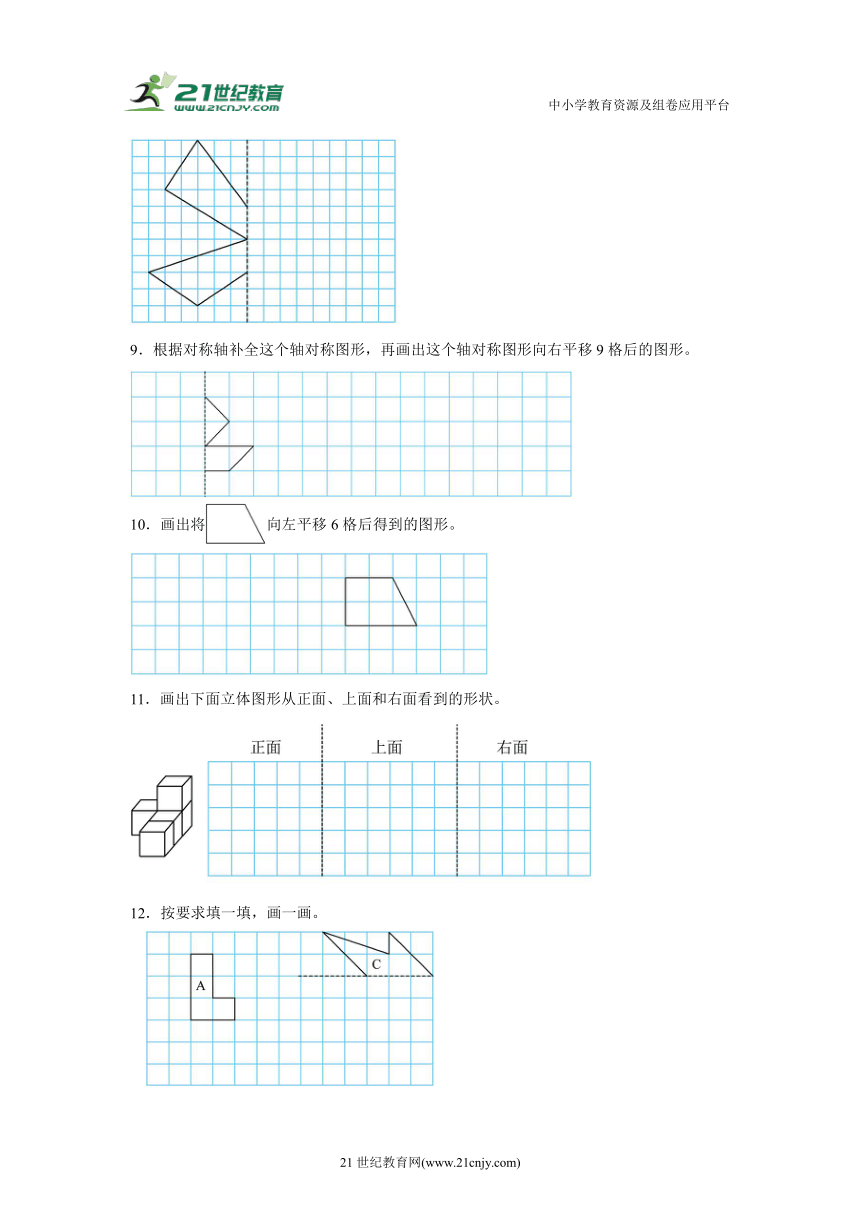
6.在方格纸上,先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移8格后的图形。
7.想一想、画一画。
(1)画出下面这个轴对称图形的另一半;
(2)把这个轴对称图形向右平移5格;
8.画出下面的图形的轴对称图形。
9.根据对称轴补全这个轴对称图形,再画出这个轴对称图形向右平移9格后的图形。
10.画出将向左平移6格后得到的图形。
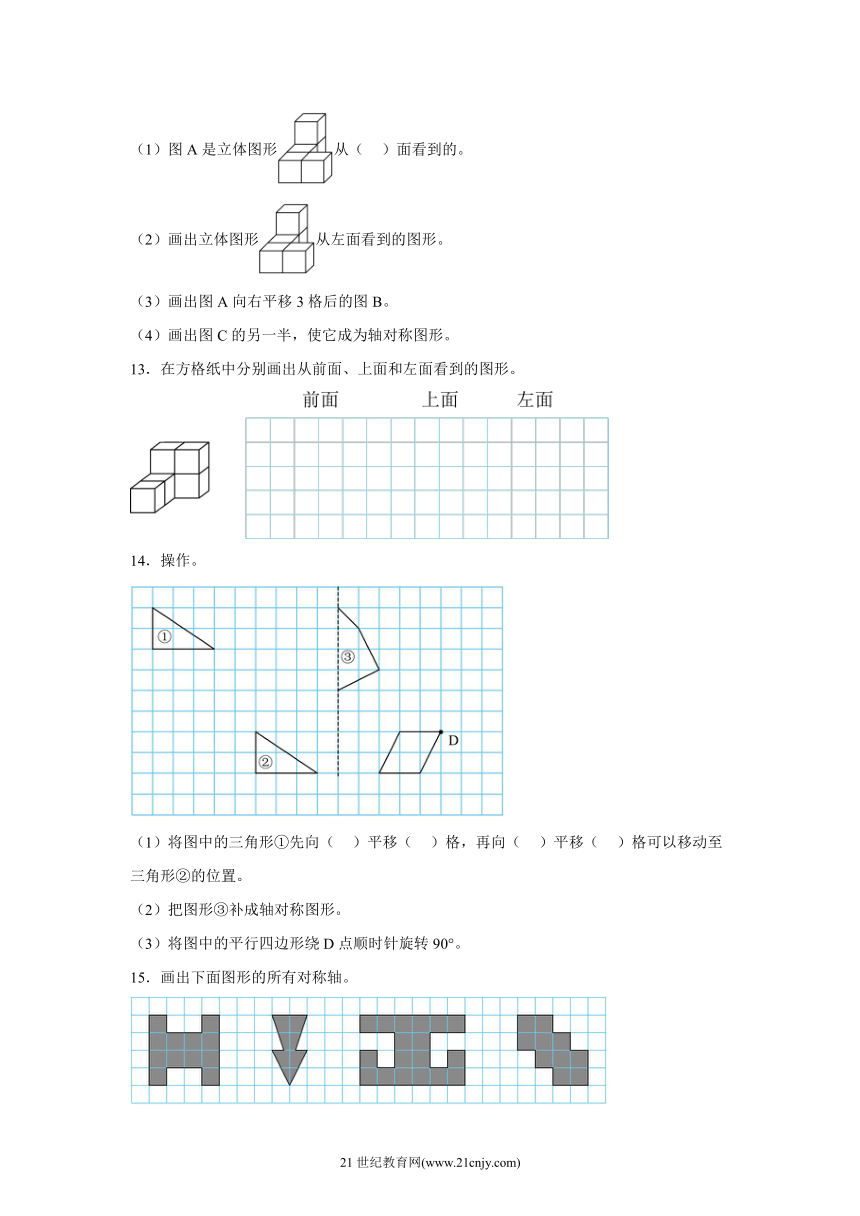
11.画出下面立体图形从正面、上面和右面看到的形状。
12.按要求填一填,画一画。
(1)图A是立体图形从( )面看到的。
(2)画出立体图形从左面看到的图形。
(3)画出图A向右平移3格后的图B。
(4)画出图C的另一半,使它成为轴对称图形。
13.在方格纸中分别画出从前面、上面和左面看到的图形。
14.操作。
(1)将图中的三角形①先向( )平移( )格,再向( )平移( )格可以移动至三角形②的位置。
(2)把图形③补成轴对称图形。
(3)将图中的平行四边形绕D点顺时针旋转90°。
15.画出下面图形的所有对称轴。
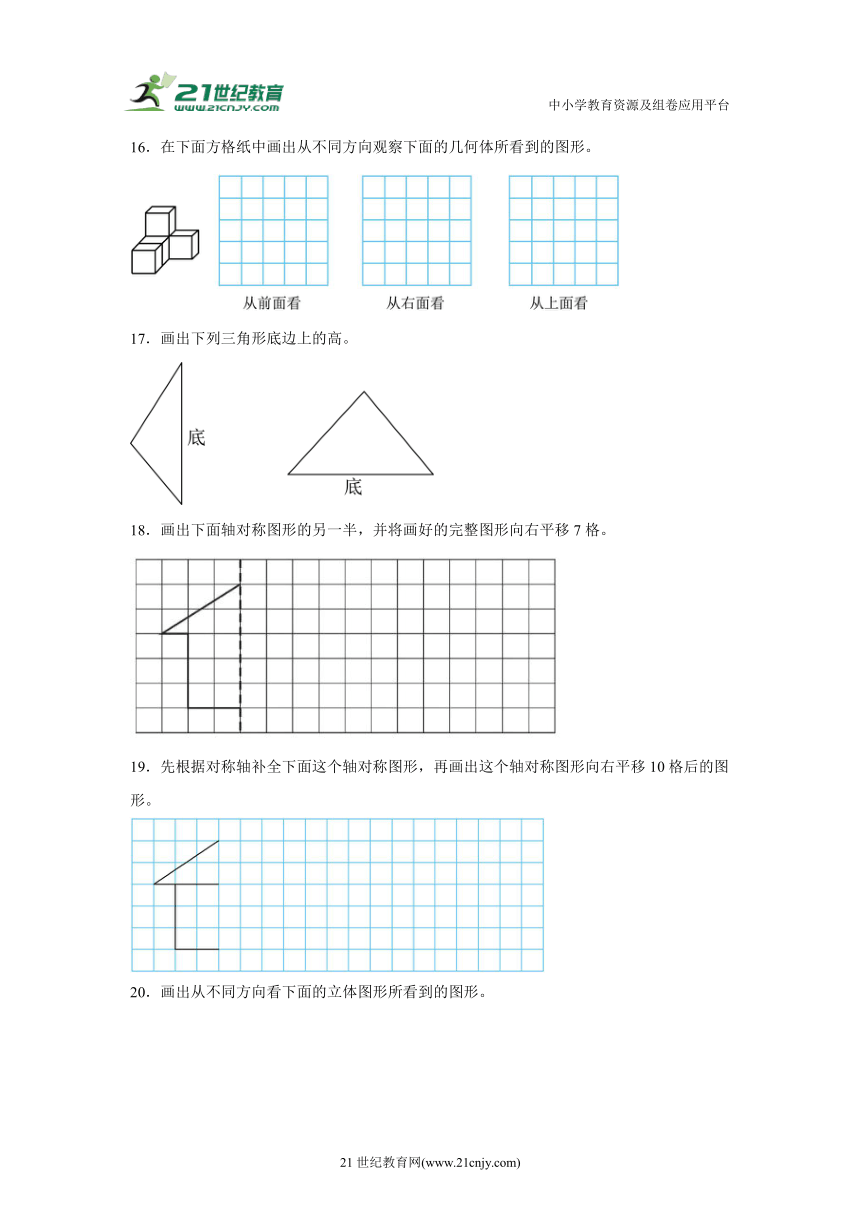
16.在下面方格纸中画出从不同方向观察下面的几何体所看到的图形。
17.画出下列三角形底边上的高。
18.画出下面轴对称图形的另一半,并将画好的完整图形向右平移7格。
19.先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移10格后的图形。
20.画出从不同方向看下面的立体图形所看到的图形。
21.下面方格纸中每个小正方形的面积代表1平方厘米,给定的这条线段长5厘米。以这条线段为一条边画一个周长是22厘米的长方形。
22.把小船图先向左平移4格,再向上平移4格;把金鱼图的另一半画出来。
23.用方格纸画出从正面、左面和上面看到的图形。
24.画一画。
先画出图①向左平移5格后的图形再画出图②的另一半,使它成为一个对称轴图形。
25.画出从前面 上面和左面看到的图形。
26.涂色表示下面的小数。
27.观察下面的物体,画出从前面、上面和左面看到的图形。
28.在直线上标出下面各数的位置。
29.在方格纸中画出从前面、左面和上面看到的图形。
30.分别画出下面用小正方体组成的几何体从上面、左面和前面看到的图形。
31.在下面方格里,画出从不同位置观察所看到的图形。
32.涂阴影表示下面各小数。
33.在方格纸上画出下面几何体从前面、上面、左面看到的图形。
34.作图题。
(1)画出①号三角形AB边上的高。
(2)画出三角形ABC以N为对称轴的轴对称图形的另一半,标注为②号。①号与②号组成了( )三角形。
(3)画出线段AB向左平移5格后的图形,标注为A'B'。
35.(1)先画出下图平行四边形的轴对称图形(虚线为对称轴)。
(2)再画出原平行四边形图先向上平移3格,再向左平移5格后的图形。
36.(1)以虚线为对称轴,补全这个轴对称图形。
(2)将这个完整的图形先向上平移3格,得到图形①,再向右平移5格得到图形②。
37.按要求作图。(每个小方格的边长表示1厘米)
(1)先画出上面这个轴对称图形的另一半,再画出这个轴对称图形向左平移6格后的图形。
(2)在合适位置画一个底是4厘米的三角形,再画出它的一条高,并标出所画的高和对应的底;所画三角形的面积是( )平方厘米。
38.先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移10格、向上平移5格后得到的图形。
39.操作。
(1)根据图中的对称轴l,画出这个轴对称图形的另一半。
(2)将补充完整的轴对称图形图形向右平移6格,画出平移后的图形。
40.涂色表示下面各小数。
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.见详解
【思路分析】根据轴对称图形的性质,对称点到对称轴的距离相等,在对称轴的另一边画出图形的几个顶点的对应点,依次连线即可。
【解析】
2.(1)(2)见详解
【思路分析】(1)补全轴对称图形:根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连结即可补全这个轴对称图形;
(2)作平移图形:根据平移的特征,把这个对称图形的各顶点分别向右平移6格,然后依次连结即可得到平移后的图形。
【解析】
3.见详解
【思路分析】从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高,这个顶点所对的边叫做三角形的底。据此作图。
【解析】
4.(1)(2)图见详解
【思路分析】(1)三个角都是锐角的三角形是锐角三角形,先画出一条线段BC,使顶点A到BC的距离为4格,再连接AB、AC,使三角形ABC为锐角三角形,过点A向对边BC作垂线,则顶点与垂足之间的线段就是这个三角形的高,据此画图即可;
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形。据此画出三角形ABC向右平移6格后得到的图形即可。
【解析】(1)(2)作图如下:
5.见详解
【思路分析】(1)补全轴对称图形的方法:找出构成图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
【解析】
6.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
7.见详解
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连结即可补全这个轴对称图形。
(2)根据平移的特征,把这个轴对称图形的各顶点分别向右平移5格,然后依次连结即可得到平移后的图形。
【解析】根据分析画图如下:
8.见详解
【思路分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线是对称轴。
补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解析】由分析得:
9.见详解
【思路分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
10.见详解
【思路分析】根据平移的特征,将图形的各顶点分别向左平移6格,依次连接即可得到平移后的图形。
【解析】如下图:
11.见详解
【思路分析】根据题意,从正面看有两行,上面一行一个小正方形右对齐,下面一行两个小正方形横着排;从上面看有三行,上面一行两个小正方形横着排,第二行和第三行均有一个小正方形右对齐;从右面看有两行,上面一行一个小正方形右对齐,下面一行三个小正方形横着排;据此画出图形。
【解析】
12.(1)上
(2)(3)(4)见详解
【思路分析】(1)(2)从前面看图A,有两层,上层1个(靠左),下层2个;从上面看图A,有三层,上层1个(靠左),中间1个(靠左),下层2个;从左面看图A,有两层,上层1个(靠左),下层3个;
(3)根据平移的特征,把图A的各顶点分别向右平移3格,依次连结即可得到向右平移3格后的图形;
(4)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图A的关键对称点,依次连结即可画出图A的另一半,使它成为一个轴对称图形。
【解析】(1)根据分析可知,图A是立体图形从上面看到的。
(2)(3)(4)如下图:
13.见详解
【思路分析】根据题意,仔细观察图形,从前面看到的图形是2层,下层是2个正方形,上层是2个正方形,并列排着;从上面看到的图形是3层,上层是2个正方形,中层下层都是1个正方形,靠左;从左面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠左边;由此画图即可。
【解析】根据分析画图如下:
14.(1)下;6;右;5
(2)(3)见详解
【思路分析】(1)结合图示信息以及所学知识可知,图形的平移是整体的平移,平移后的大小形状不发生改变,故实际解答的时候往往可以根据三角形①图形上某一个对应点来判断平移。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
【解析】(1)找到三角形的一个顶点,据此判断可得:将图中的三角形①先向下平移6格(或向右平移5格),再向右平移5格(或向下平移6格)即可移动至三角形②的位置。
(2)(3)如图所示:
15.见详解
【思路分析】一个图形沿一条直线对折后,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。画对称轴的步骤:找出轴对称图形的任意一组对称点,连结对称点,画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。据此画出每个图形的所有对称轴即可。
【解析】
16.见详解
【思路分析】从前面看,看到的是两层,下层2个小正方形,上层1个小正方形靠左对齐;从右面看,看到的也是两层,下层3个小正方形,上层1个小正方形靠右对齐;从上面看,看到的是三层,最上层是2个小正方形,下面两层各有1个小正方形靠左对齐。
【解析】
17.图见详解
【思路分析】作三角形高的方法是:先找到三角形的顶点和对应的边,然后在对应边上放一把三角尺,让三角尺和这条边保持垂直,接着移动三角尺,当三角尺的另一边和顶点重合时,就连接顶点和三角尺直角与对应边的重合点,这条线段就是三角形底边上的高。
【解析】如下图:
18.见详解
【思路分析】如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形。
【解析】如图:
19.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】如下图:
20.见详解
【思路分析】从正面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有2行,上面1行2个小正方形,下面1行2个小正方形,上面一行右侧小正方形和下面一行左侧小正方形对齐;从右面看,共有2行,上面1行1个小正方形,下面1行2个小正方形,右对齐;据此画出从不同方向所看到的图形即可。
【解析】
21.图见详解
【思路分析】根据长方形周长=(长+宽)×2,先用周长÷2算出长与宽的和,再结合已知的一条边(宽)的长度,用减法求出长方形另一条边(长)的长度,最后根据长和宽在方格纸上画出长方形。
【解析】22÷2-5
=11-5
=6(厘米)
画出的长方形长是6厘米,宽是5厘米:
22.见详解
【思路分析】作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形;
根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出这个图形的关键对称点,依次连接即可补全下面这个轴对称图形。
【解析】如图:
23.见详解
【思路分析】从正面看到的图形是两层:下层3个正方形,上层2个正方形,分别左右对齐;从上面看到的图形是两层:上层3个正方形,下层2个正方形,左齐;从左面看到的图形是两层:下层2个正方形,上层1个正方形,左齐;据此即可画图。
【解析】据分析作图如下:
24.见详解
【思路分析】根据题意,图形平移的方法是点对点平移,把图①的各顶点分别向左平移5格,依次连接各点即可得到平移后的图形。根据轴对称图形的特征,对称点到对称轴的距离相等,在对称轴(虚线)的右边画出图②的各对称点,依次连接各点即可。
【解析】根据分析画图如下:
25.见详解
【思路分析】从前面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有3行,上面1行3个小正方形,下面1行1个小正方形,中间1行1个小正方形,右对齐;从左面看,共有2行,上面1行1个小正方形,下面1行3个小正方形,左对齐,据此解答即可。
【解析】
26.见详解
【思路分析】(1)把一个正方形涂满,它表示整数部分1,另一个正方形平均分成10份,取其中的3份,就是0.3,把这两个部分合在一起就是1.3;
(2)0.045m表示把1m平均分成1000份,根据1m=1000mm,所以每份是1mm,则45份就是45mm;右上图1小格表示1mm,画45个小格即表示45mm,据此画图。
【解析】如下图:
27.见详解
【思路分析】从前面看,一共两层,从上往下看,第一层左边和中间各有一个小正方形,第二层有三个小正方形;从上面看,一共两层,从上往下看,第一层有三个小正方形,第二层左边和右边各有一个小正方形;从左面看,一共两层,从上往下看,第一层左上角有一个小正方形,第二层有两个小正方形;据此画图。
【解析】
28.见详解
【思路分析】观察可知,直线上的1大格被平均分成10份,每小格代表0.1。1大格被平均分成100份,每份就是0.01。
0.7在0~1之间的第7小格处;1.35在1~2之间的第3小格和第4小格的中间;3.2在3~4之间的第2小格处;据此在直线上标出这3个数的位置。
【解析】各数的位置如下所示:
29.画图见详解
【思路分析】根据图意可知,从前面看有两层,上层有2个正方形,左右各1个,中间没有,下层有3个正方形;从左面看有1列2层,每层各1个正方形;从上面看有1层3个正方形。
【解析】
30.见详解
【思路分析】根据物体三视图的认识和画法,该物体从上面能看到3个相同的小正方形,分两层,上层1个下层2个,一共有3列,上层的在最右边的一列,下层的在左边的两列;从左面能看到5个相同的小正方形,分三层,上层1个中间层2个下层2个,右齐;从前面能看到6个相同的小正方形,分三层,上层1个中间层2个下层3个,一共有3列,上层的在最左边的一列,中间层的在左右两列,下层的正好在3列,据此作图即可。
【解析】
如图:
31.见详解
【思路分析】从前面看两行,下面一行3个,上面一行1个,左对齐;
从左面看两列,左面一列1个,右面一列2个;
从上面看两行,下面一行3个,上面一行1个,右对齐;
【解析】如图:
32.见详解
【思路分析】0.5表示把一个正方形平均分成10份,涂其中的5份是0.5;
0.06米根据1米=100厘米,把1米平均分成100份,涂其中的6份是6厘米,也是0.06米;
1.3的整数部分是1表示有一个图形要全部涂满,小数部分是0.3表示把另一个图形平均分成10份,涂另一个图形中的3份,即把一个图形涂满,另一个图形涂其中的3份即可;
【解析】
33.见详解
【思路分析】观察图形,从前面看到两行,下面一行是3个正方形,上面一行是1个正方形,左对齐。从上面看到两行,下面一行是2个正方形,上面一行是2个正方形,上面一行右边的正方形与下面一行左面的正方形对齐。从左面看到两行,下面一行是2个正方形,上面一行是1个正方形,左对齐。
【解析】
34.(1)图见详解;
(2)图见详解;等腰直角
(3)图见详解;
【思路分析】(1)根据三角形高的画法,从三角形的一个顶点C到它的对边AB做一条垂线,顶点的垂足之间的线段,就是三角形的高,画出三角形ABC中AB边上的高即可;
(2)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形;在三角形中,两条边相等的三角形叫作等腰三角形,有一个角是直角的等腰三角形是等腰直角三角形;
(3)作平移后的图形步骤:找出构成图形的关键点,确定平移方向和平移距离,由平移的距离确定关键点平移后的对应点的位置,连接对应点;据此作图。
【解析】(1)三角形AB边上的高如图:
(2)三角形ABC以N为对称轴的轴对称图形的另一半如图:
根据图示可知,BC=AC,∠BCA是直角,所以①号三角形是直角等腰三角形;用三角形的内角和180°减去90°,就得到另外两个角的和是90°,又因为等腰三角形的两个底角相同,所以∠CBA和∠BAC都是45°;根据轴对称的性质可知,AB=AD,∠DAC是45°,所以∠BAD是一个直角,所以①号与②号组成了等腰直角三角形;
(3)如图:
35.(1)见详解
(2)见详解
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的另一边画出关键对称点,依次连接即可画出轴对称图形。
(2)根据平移图形的特征,把图形的各点分别先向上平移3格,再向左平移5格,依次连接各点即可得到平移后的图形。
【解析】根据分析画图如下:
(1)(2)
36.见详解
【思路分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可。
物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
【解析】
37.(1)见详解;(2)图见详解;6(答案不唯一)
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)画一个底是4厘米的三角形(占小方格的边长4个),在垂直方向位置画出高,比如3厘米(占小方格的边长3个),再连接另外两边;从图中观察所画三角形面积是等底等高的长方形面积的一半,长方形面积=长×宽,再除以2即为三角形面积。
【解析】(2)4×3÷2
=12÷2
=6(平方厘米)
所画三角形的面积是(6)平方厘米。(答案不唯一)
(1)(2)作图如下:
(三角形的画法不唯一)
38.图见详解
【思路分析】如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出这个轴对称图形向右平移10格、向上平移5格后得到的图形。
【解析】
39.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
40.见详解
【思路分析】(1)0.6表示把这个正方形平均分成10份,涂色部分占其中的6份。
(2)0.36表示把这个正方形平均分成100份,涂色部分占其中的36份。
(3)1.2表示一个完整的长方形和一个被平均分成10份,取其中的2份的长方形合在一起,以此涂色即可。
【解析】根据分析涂色如下:
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
专项05 操作题
学校:___________姓名:___________班级:___________考号:___________
1.根据对称轴补全下面轴对称图形。
2.根据要求在方格纸上画图。
(1)根据对称轴补全下面这个轴对称图形。
(2)画出这个轴对称图形向右平移6个格后的图形。
3.画出下面三角形指定底边上的高,并标出“高”。
4.按要求在下面方格纸上画一画。
(1)先在方格纸上画一个高是4厘米的锐角三角形ABC,并画出这条高。
(2)画出将三角形ABC向右平移6格后得到的图形。
5.想一想,画一画。
(1)根据对称轴,画出上面轴对称图形的另一半。
(2)画出这个轴对称图形向左平移6格后的图形。
(3)画出三角形ABC的一条边AB上的高。
6.在方格纸上,先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移8格后的图形。
7.想一想、画一画。
(1)画出下面这个轴对称图形的另一半;
(2)把这个轴对称图形向右平移5格;
8.画出下面的图形的轴对称图形。
9.根据对称轴补全这个轴对称图形,再画出这个轴对称图形向右平移9格后的图形。
10.画出将向左平移6格后得到的图形。
11.画出下面立体图形从正面、上面和右面看到的形状。
12.按要求填一填,画一画。
(1)图A是立体图形从( )面看到的。
(2)画出立体图形从左面看到的图形。
(3)画出图A向右平移3格后的图B。
(4)画出图C的另一半,使它成为轴对称图形。
13.在方格纸中分别画出从前面、上面和左面看到的图形。
14.操作。
(1)将图中的三角形①先向( )平移( )格,再向( )平移( )格可以移动至三角形②的位置。
(2)把图形③补成轴对称图形。
(3)将图中的平行四边形绕D点顺时针旋转90°。
15.画出下面图形的所有对称轴。
16.在下面方格纸中画出从不同方向观察下面的几何体所看到的图形。
17.画出下列三角形底边上的高。
18.画出下面轴对称图形的另一半,并将画好的完整图形向右平移7格。
19.先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移10格后的图形。
20.画出从不同方向看下面的立体图形所看到的图形。
21.下面方格纸中每个小正方形的面积代表1平方厘米,给定的这条线段长5厘米。以这条线段为一条边画一个周长是22厘米的长方形。
22.把小船图先向左平移4格,再向上平移4格;把金鱼图的另一半画出来。
23.用方格纸画出从正面、左面和上面看到的图形。
24.画一画。
先画出图①向左平移5格后的图形再画出图②的另一半,使它成为一个对称轴图形。
25.画出从前面 上面和左面看到的图形。
26.涂色表示下面的小数。
27.观察下面的物体,画出从前面、上面和左面看到的图形。
28.在直线上标出下面各数的位置。
29.在方格纸中画出从前面、左面和上面看到的图形。
30.分别画出下面用小正方体组成的几何体从上面、左面和前面看到的图形。
31.在下面方格里,画出从不同位置观察所看到的图形。
32.涂阴影表示下面各小数。
33.在方格纸上画出下面几何体从前面、上面、左面看到的图形。
34.作图题。
(1)画出①号三角形AB边上的高。
(2)画出三角形ABC以N为对称轴的轴对称图形的另一半,标注为②号。①号与②号组成了( )三角形。
(3)画出线段AB向左平移5格后的图形,标注为A'B'。
35.(1)先画出下图平行四边形的轴对称图形(虚线为对称轴)。
(2)再画出原平行四边形图先向上平移3格,再向左平移5格后的图形。
36.(1)以虚线为对称轴,补全这个轴对称图形。
(2)将这个完整的图形先向上平移3格,得到图形①,再向右平移5格得到图形②。
37.按要求作图。(每个小方格的边长表示1厘米)
(1)先画出上面这个轴对称图形的另一半,再画出这个轴对称图形向左平移6格后的图形。
(2)在合适位置画一个底是4厘米的三角形,再画出它的一条高,并标出所画的高和对应的底;所画三角形的面积是( )平方厘米。
38.先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移10格、向上平移5格后得到的图形。
39.操作。
(1)根据图中的对称轴l,画出这个轴对称图形的另一半。
(2)将补充完整的轴对称图形图形向右平移6格,画出平移后的图形。
40.涂色表示下面各小数。
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.见详解
【思路分析】根据轴对称图形的性质,对称点到对称轴的距离相等,在对称轴的另一边画出图形的几个顶点的对应点,依次连线即可。
【解析】
2.(1)(2)见详解
【思路分析】(1)补全轴对称图形:根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连结即可补全这个轴对称图形;
(2)作平移图形:根据平移的特征,把这个对称图形的各顶点分别向右平移6格,然后依次连结即可得到平移后的图形。
【解析】
3.见详解
【思路分析】从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高,这个顶点所对的边叫做三角形的底。据此作图。
【解析】
4.(1)(2)图见详解
【思路分析】(1)三个角都是锐角的三角形是锐角三角形,先画出一条线段BC,使顶点A到BC的距离为4格,再连接AB、AC,使三角形ABC为锐角三角形,过点A向对边BC作垂线,则顶点与垂足之间的线段就是这个三角形的高,据此画图即可;
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形。据此画出三角形ABC向右平移6格后得到的图形即可。
【解析】(1)(2)作图如下:
5.见详解
【思路分析】(1)补全轴对称图形的方法:找出构成图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
【解析】
6.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
7.见详解
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连结即可补全这个轴对称图形。
(2)根据平移的特征,把这个轴对称图形的各顶点分别向右平移5格,然后依次连结即可得到平移后的图形。
【解析】根据分析画图如下:
8.见详解
【思路分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线是对称轴。
补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解析】由分析得:
9.见详解
【思路分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
10.见详解
【思路分析】根据平移的特征,将图形的各顶点分别向左平移6格,依次连接即可得到平移后的图形。
【解析】如下图:
11.见详解
【思路分析】根据题意,从正面看有两行,上面一行一个小正方形右对齐,下面一行两个小正方形横着排;从上面看有三行,上面一行两个小正方形横着排,第二行和第三行均有一个小正方形右对齐;从右面看有两行,上面一行一个小正方形右对齐,下面一行三个小正方形横着排;据此画出图形。
【解析】
12.(1)上
(2)(3)(4)见详解
【思路分析】(1)(2)从前面看图A,有两层,上层1个(靠左),下层2个;从上面看图A,有三层,上层1个(靠左),中间1个(靠左),下层2个;从左面看图A,有两层,上层1个(靠左),下层3个;
(3)根据平移的特征,把图A的各顶点分别向右平移3格,依次连结即可得到向右平移3格后的图形;
(4)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图A的关键对称点,依次连结即可画出图A的另一半,使它成为一个轴对称图形。
【解析】(1)根据分析可知,图A是立体图形从上面看到的。
(2)(3)(4)如下图:
13.见详解
【思路分析】根据题意,仔细观察图形,从前面看到的图形是2层,下层是2个正方形,上层是2个正方形,并列排着;从上面看到的图形是3层,上层是2个正方形,中层下层都是1个正方形,靠左;从左面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠左边;由此画图即可。
【解析】根据分析画图如下:
14.(1)下;6;右;5
(2)(3)见详解
【思路分析】(1)结合图示信息以及所学知识可知,图形的平移是整体的平移,平移后的大小形状不发生改变,故实际解答的时候往往可以根据三角形①图形上某一个对应点来判断平移。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
【解析】(1)找到三角形的一个顶点,据此判断可得:将图中的三角形①先向下平移6格(或向右平移5格),再向右平移5格(或向下平移6格)即可移动至三角形②的位置。
(2)(3)如图所示:
15.见详解
【思路分析】一个图形沿一条直线对折后,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。画对称轴的步骤:找出轴对称图形的任意一组对称点,连结对称点,画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。据此画出每个图形的所有对称轴即可。
【解析】
16.见详解
【思路分析】从前面看,看到的是两层,下层2个小正方形,上层1个小正方形靠左对齐;从右面看,看到的也是两层,下层3个小正方形,上层1个小正方形靠右对齐;从上面看,看到的是三层,最上层是2个小正方形,下面两层各有1个小正方形靠左对齐。
【解析】
17.图见详解
【思路分析】作三角形高的方法是:先找到三角形的顶点和对应的边,然后在对应边上放一把三角尺,让三角尺和这条边保持垂直,接着移动三角尺,当三角尺的另一边和顶点重合时,就连接顶点和三角尺直角与对应边的重合点,这条线段就是三角形底边上的高。
【解析】如下图:
18.见详解
【思路分析】如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形。
【解析】如图:
19.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】如下图:
20.见详解
【思路分析】从正面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有2行,上面1行2个小正方形,下面1行2个小正方形,上面一行右侧小正方形和下面一行左侧小正方形对齐;从右面看,共有2行,上面1行1个小正方形,下面1行2个小正方形,右对齐;据此画出从不同方向所看到的图形即可。
【解析】
21.图见详解
【思路分析】根据长方形周长=(长+宽)×2,先用周长÷2算出长与宽的和,再结合已知的一条边(宽)的长度,用减法求出长方形另一条边(长)的长度,最后根据长和宽在方格纸上画出长方形。
【解析】22÷2-5
=11-5
=6(厘米)
画出的长方形长是6厘米,宽是5厘米:
22.见详解
【思路分析】作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形;
根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出这个图形的关键对称点,依次连接即可补全下面这个轴对称图形。
【解析】如图:
23.见详解
【思路分析】从正面看到的图形是两层:下层3个正方形,上层2个正方形,分别左右对齐;从上面看到的图形是两层:上层3个正方形,下层2个正方形,左齐;从左面看到的图形是两层:下层2个正方形,上层1个正方形,左齐;据此即可画图。
【解析】据分析作图如下:
24.见详解
【思路分析】根据题意,图形平移的方法是点对点平移,把图①的各顶点分别向左平移5格,依次连接各点即可得到平移后的图形。根据轴对称图形的特征,对称点到对称轴的距离相等,在对称轴(虚线)的右边画出图②的各对称点,依次连接各点即可。
【解析】根据分析画图如下:
25.见详解
【思路分析】从前面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有3行,上面1行3个小正方形,下面1行1个小正方形,中间1行1个小正方形,右对齐;从左面看,共有2行,上面1行1个小正方形,下面1行3个小正方形,左对齐,据此解答即可。
【解析】
26.见详解
【思路分析】(1)把一个正方形涂满,它表示整数部分1,另一个正方形平均分成10份,取其中的3份,就是0.3,把这两个部分合在一起就是1.3;
(2)0.045m表示把1m平均分成1000份,根据1m=1000mm,所以每份是1mm,则45份就是45mm;右上图1小格表示1mm,画45个小格即表示45mm,据此画图。
【解析】如下图:
27.见详解
【思路分析】从前面看,一共两层,从上往下看,第一层左边和中间各有一个小正方形,第二层有三个小正方形;从上面看,一共两层,从上往下看,第一层有三个小正方形,第二层左边和右边各有一个小正方形;从左面看,一共两层,从上往下看,第一层左上角有一个小正方形,第二层有两个小正方形;据此画图。
【解析】
28.见详解
【思路分析】观察可知,直线上的1大格被平均分成10份,每小格代表0.1。1大格被平均分成100份,每份就是0.01。
0.7在0~1之间的第7小格处;1.35在1~2之间的第3小格和第4小格的中间;3.2在3~4之间的第2小格处;据此在直线上标出这3个数的位置。
【解析】各数的位置如下所示:
29.画图见详解
【思路分析】根据图意可知,从前面看有两层,上层有2个正方形,左右各1个,中间没有,下层有3个正方形;从左面看有1列2层,每层各1个正方形;从上面看有1层3个正方形。
【解析】
30.见详解
【思路分析】根据物体三视图的认识和画法,该物体从上面能看到3个相同的小正方形,分两层,上层1个下层2个,一共有3列,上层的在最右边的一列,下层的在左边的两列;从左面能看到5个相同的小正方形,分三层,上层1个中间层2个下层2个,右齐;从前面能看到6个相同的小正方形,分三层,上层1个中间层2个下层3个,一共有3列,上层的在最左边的一列,中间层的在左右两列,下层的正好在3列,据此作图即可。
【解析】
如图:
31.见详解
【思路分析】从前面看两行,下面一行3个,上面一行1个,左对齐;
从左面看两列,左面一列1个,右面一列2个;
从上面看两行,下面一行3个,上面一行1个,右对齐;
【解析】如图:
32.见详解
【思路分析】0.5表示把一个正方形平均分成10份,涂其中的5份是0.5;
0.06米根据1米=100厘米,把1米平均分成100份,涂其中的6份是6厘米,也是0.06米;
1.3的整数部分是1表示有一个图形要全部涂满,小数部分是0.3表示把另一个图形平均分成10份,涂另一个图形中的3份,即把一个图形涂满,另一个图形涂其中的3份即可;
【解析】
33.见详解
【思路分析】观察图形,从前面看到两行,下面一行是3个正方形,上面一行是1个正方形,左对齐。从上面看到两行,下面一行是2个正方形,上面一行是2个正方形,上面一行右边的正方形与下面一行左面的正方形对齐。从左面看到两行,下面一行是2个正方形,上面一行是1个正方形,左对齐。
【解析】
34.(1)图见详解;
(2)图见详解;等腰直角
(3)图见详解;
【思路分析】(1)根据三角形高的画法,从三角形的一个顶点C到它的对边AB做一条垂线,顶点的垂足之间的线段,就是三角形的高,画出三角形ABC中AB边上的高即可;
(2)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形;在三角形中,两条边相等的三角形叫作等腰三角形,有一个角是直角的等腰三角形是等腰直角三角形;
(3)作平移后的图形步骤:找出构成图形的关键点,确定平移方向和平移距离,由平移的距离确定关键点平移后的对应点的位置,连接对应点;据此作图。
【解析】(1)三角形AB边上的高如图:
(2)三角形ABC以N为对称轴的轴对称图形的另一半如图:
根据图示可知,BC=AC,∠BCA是直角,所以①号三角形是直角等腰三角形;用三角形的内角和180°减去90°,就得到另外两个角的和是90°,又因为等腰三角形的两个底角相同,所以∠CBA和∠BAC都是45°;根据轴对称的性质可知,AB=AD,∠DAC是45°,所以∠BAD是一个直角,所以①号与②号组成了等腰直角三角形;
(3)如图:
35.(1)见详解
(2)见详解
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的另一边画出关键对称点,依次连接即可画出轴对称图形。
(2)根据平移图形的特征,把图形的各点分别先向上平移3格,再向左平移5格,依次连接各点即可得到平移后的图形。
【解析】根据分析画图如下:
(1)(2)
36.见详解
【思路分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可。
物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
【解析】
37.(1)见详解;(2)图见详解;6(答案不唯一)
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)画一个底是4厘米的三角形(占小方格的边长4个),在垂直方向位置画出高,比如3厘米(占小方格的边长3个),再连接另外两边;从图中观察所画三角形面积是等底等高的长方形面积的一半,长方形面积=长×宽,再除以2即为三角形面积。
【解析】(2)4×3÷2
=12÷2
=6(平方厘米)
所画三角形的面积是(6)平方厘米。(答案不唯一)
(1)(2)作图如下:
(三角形的画法不唯一)
38.图见详解
【思路分析】如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出这个轴对称图形向右平移10格、向上平移5格后得到的图形。
【解析】
39.见详解
【思路分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【解析】
40.见详解
【思路分析】(1)0.6表示把这个正方形平均分成10份,涂色部分占其中的6份。
(2)0.36表示把这个正方形平均分成100份,涂色部分占其中的36份。
(3)1.2表示一个完整的长方形和一个被平均分成10份,取其中的2份的长方形合在一起,以此涂色即可。
【解析】根据分析涂色如下:
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
