3.1.1代数式 课件(共34张PPT)
文档属性
| 名称 | 3.1.1代数式 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 15:05:01 | ||
图片预览











文档简介
(共34张PPT)
人教版数学七年级上册
第三章 代数式
汇报人:孙老师
汇报班级:X级X班
3.1 列代数式表示数量关系
3.1.1代数式
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解代数式的基本概念,能正确认识代数式.
2.掌握代数式的书写要求,能根据代数式的类型正确书写代数式.
3.理解代数式的意义,明白每个符号代表的意义以及整个式子所表示的数量关系.
第贰章节
新课导入
新课导入
新课导入
智能机器人的广泛应用是智慧农业的发展趋势之一. 某品牌苹果采摘机器人平均每秒可以完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手平均 8 s 可以采摘一个苹果. 根据这些数据回答下列问题:
(1)该机器人 10 s 能识别多大范围内的苹果?60 s 呢?t s 呢?
(2)该机器人识别 n m2 范围内的苹果需要多少秒?
(3)若该机器人搭载了 m 个机械手(m > 1),它与采摘工人同时工作 1 h,已知工人平均 5 s 可以采摘一个苹果,则机器人可比工人多采摘多少个苹果?
回答上面的问题,要用到含有字母的式子.
第叁章节
新知探究
新知探究
知识点1:字母表示数
问题 智能机器人的广泛应用是智慧农业的发展越势之一. 某品牌苹果采摘机器人可以 1 s 完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手 8 s 可以采摘一个苹果,根据这些数据回答下列问题:
(1) 该机器人 10 s 能识别
多大范围内的苹果
60 s 呢 t s 呢
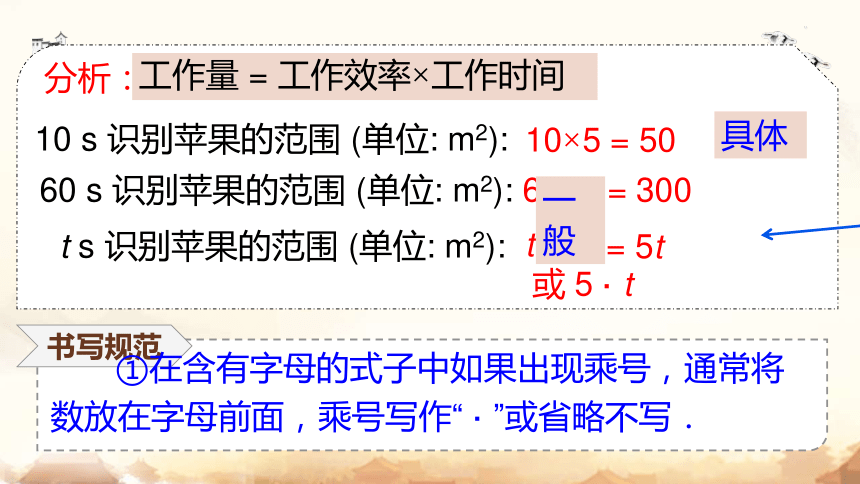
工作量 = 工作效率×工作时间
10 s 识别苹果的范围 (单位: m2):
60 s 识别苹果的范围 (单位: m2):
t s 识别苹果的范围 (单位: m2):
= 5t
10×5 = 50
60×5 = 300
分析:
t×5
或 5 · t
具体
一般
书写规范
①在含有字母的式子中如果出现乘号,通常将数放在字母前面,乘号写作“ · ”或省略不写.
(2) 该机器人识别 n m2 范围内的苹果需要多少秒
工作时间 = 工作量÷工作效率
背景:某品牌苹果采摘机器人可以 1 s 完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手 8 s 可以采摘一个苹果.
书写规范
②除法运算写成分数形式,即除号改为分数线.
用字母表示数
分析:机器人多采摘苹果个数
= 机器人采摘的苹果个数 一 工人采摘的苹果个数
= 机器人的采摘效率×工作时间
一 工人采摘效率×工作时间
(3) 若该机器人搭载了 10 个机械手,它与采摘工人同时工作 1 h,假设工人 m s 可以采摘一个苹果,则机器人可比工人多采摘多少个苹果
用字母表示数量关系
(1) 一条河的水流速度是 2.5 km/h. 船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶的速度;
用含有字母的式子表示数量和数量关系的问题.
合作探究
顺水时
逆水时
船的速度=船在静水中的速度+水流速度
船的速度=船在静水中的速度-水流速度
行船问题
分析:
解:船在这条河中顺水行驶的速度是 (v+2.5) km/h,逆水行驶的速度是 (v-2.5) km/h.
书写规范
③后面带单位的相加或相减的式子要用括号括起来.
(2)一个正方形的边长是 a,这个正方形的周长 l 是多少?面积 S 呢
解:由正方形的周长=4×边长,
正方形的面积=边长×边长, 得
书写规范
④相同字母相乘时,结果需要写成幂的形式.
l=4a,
S=a2.
定义总结
想一想:这些式子都有什么样的特点?
它们都是用运算符号把数或表示数的字母连接起来的式子,
我们称这样的式子为代数式.
单独的一个数或字母也是代数式.
例如,5,t 都是代数式.
方法:(1) 代数式中不含表示数量关系的符号,如“=”“>”“<”“≥”“≤”“≠”等 .
(2) 单独的一个数或字母也是代数式.
例1 下列各式中哪些是代数式?哪些不是?
(1)m + 5 (2)a + b = b + a (3)0
(4)x + 3x + 4 (5)x + y>1 (6)
√
×
√
√
×
√
典例精析
典例精析
例2 (1) 苹果原价是 p 元/kg. 现在按九折优惠出售,用代数式表示苹果的售价:
解:现价是每千克 0.9p 元.
现价 = 原价×折扣 (0.9)
分析:
(2) 一个长方形的长是 0.9 m,宽是 p m. 用代数式表示这个长方形的面积;
解:长方形的面积为 0.9p m2.
(3) 某产品前年的产量是 n 件,去年的产量比前年产量的 2 倍少 10 件,用代数式表示去年的产量;
(4) 一个长方体水池底面的长和宽都是 a m,高是 h m, 池内水的体积占水池容积的三分之一,用代数式表示池内水的体积.
解:由长方体的体积=长×宽×高,得
这个长方体水池的容积是 a · a · h cm3,即 a2h cm3.
解:去年的产量是 ( 2n-10 ) 件.
故池内水的体积为 cm3.
练一练
1. (1) 某产品前年的产量是 n 件,去年的产量是前年产量的 m 倍,用代数式表示去年的产量;
解:去年的产量是 mn 件.
书写规范
⑤字母与字母相乘时,按字母表顺序排列.
(3) 用式子表示数 n 的相反数.
解:数 n 的相反数是-n.
书写规范
⑦ 当“1”与字母相乘时,“1”省略不写;
当“-1”与字母相乘时,只需在该字母前加上“-”号.
(2) 若每斤苹果 元,则买 m 斤苹果需 元.
书写规范
⑥带分数与字母相乘时,把带分数化成假分数.
想一想
知识点2:代数式的意义
在例 1 中“0.9p”代数式的意义是什么?
实际意义是什么?
实际意义:(1) 苹果的售价;(2) 长方形的面积.
总结
用字母表示数后,同一个代数式可以表示不同实际问题中的数量或数量关系.
代数式的意义:p 的 0.9 倍.
例2 说出下列代数式的意义:
典例精析
(1) 2a+3; (2) 2(a+3); (3) ; (4) x2+2x+8.
(4) x2+2x+8 的意义是 x 的平方,x 的 2 倍,与 8 的和.
解:(1) 2a+3 的意义是 a 的 2 倍与 3 的和;
(2) 2(a+3) 的意义是 a 与 3 的和的 2 倍;
(3) 的意义是 c 除以 a,b 的积的商;
变式 下列代数式可以表示什么实际意义呢?
(1)2a-b; (2)2(a-b).
解:(1)若篮球的单价是 a 元,足球的单价是 b 元,则 2a - b 可表示买两个篮球比买一个足球多花的钱数.
(2)若某商店的一台学习机的售价为 a 元,进价为 b 元,则 2(a - b) 可表示该商店卖出两台学习机的盈利.
答案不唯一.
想一想
字母表示数的含义:
数量
数量关系
计算公式
运算律
2n
s = vt
C = 2(a + b)
a+b = b+a
n只青蛙的眼睛的数量
s表示路程,v表示速度,t表示时间
长方形周长
加法交换律
仿照例子,你还能写出其他式子吗?
第肆章节
随堂练习
随堂练习
【教材P71】
1. 填空题.
(1)每包书有 10 册,6 包书有_____册,n 包书有______册;
(2)王芳今年 m 岁,她去年_______岁,6 年后________岁;
60
10n
(m-1)
(m+6)
(3)将 p kg 糖装入 n 个包装袋中,每袋糖的质量相同,每袋装入糖______kg;
(4)棱长为 a 的正方体的体积是_______.
p
n
a3
2. 说出下列代数式的意义:
(1)2a + 3c;(2)3(m-n);(3)a2 + 1;(4) .
3a
5b
解:(1)a 的 2 倍与 c 的 3 倍的和;
(2)m 与 n 的差的 3 倍;
(3)a 的平方与 1 的和;
(4)a 的 3 倍除以 b 的 5 倍的商.
3. 代数式 100-2x 可以表示不同实际问题中的数量或数量关系,请举例说明.
A、B 两地相距 100 km,一辆汽车以平均速度 x km/h,从 A 地出发,行驶 2 h后,距离 B 地还有(100-2x)千米.
第伍章节
课堂小结
课堂小结
代数式
代数式的定义
代数式的意义
代数式的书写要求
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学七年级上册
第三章 代数式
汇报人:孙老师
汇报班级:X级X班
3.1 列代数式表示数量关系
3.1.1代数式
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解代数式的基本概念,能正确认识代数式.
2.掌握代数式的书写要求,能根据代数式的类型正确书写代数式.
3.理解代数式的意义,明白每个符号代表的意义以及整个式子所表示的数量关系.
第贰章节
新课导入
新课导入
新课导入
智能机器人的广泛应用是智慧农业的发展趋势之一. 某品牌苹果采摘机器人平均每秒可以完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手平均 8 s 可以采摘一个苹果. 根据这些数据回答下列问题:
(1)该机器人 10 s 能识别多大范围内的苹果?60 s 呢?t s 呢?
(2)该机器人识别 n m2 范围内的苹果需要多少秒?
(3)若该机器人搭载了 m 个机械手(m > 1),它与采摘工人同时工作 1 h,已知工人平均 5 s 可以采摘一个苹果,则机器人可比工人多采摘多少个苹果?
回答上面的问题,要用到含有字母的式子.
第叁章节
新知探究
新知探究
知识点1:字母表示数
问题 智能机器人的广泛应用是智慧农业的发展越势之一. 某品牌苹果采摘机器人可以 1 s 完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手 8 s 可以采摘一个苹果,根据这些数据回答下列问题:
(1) 该机器人 10 s 能识别
多大范围内的苹果
60 s 呢 t s 呢
工作量 = 工作效率×工作时间
10 s 识别苹果的范围 (单位: m2):
60 s 识别苹果的范围 (单位: m2):
t s 识别苹果的范围 (单位: m2):
= 5t
10×5 = 50
60×5 = 300
分析:
t×5
或 5 · t
具体
一般
书写规范
①在含有字母的式子中如果出现乘号,通常将数放在字母前面,乘号写作“ · ”或省略不写.
(2) 该机器人识别 n m2 范围内的苹果需要多少秒
工作时间 = 工作量÷工作效率
背景:某品牌苹果采摘机器人可以 1 s 完成 5 m2 范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手 8 s 可以采摘一个苹果.
书写规范
②除法运算写成分数形式,即除号改为分数线.
用字母表示数
分析:机器人多采摘苹果个数
= 机器人采摘的苹果个数 一 工人采摘的苹果个数
= 机器人的采摘效率×工作时间
一 工人采摘效率×工作时间
(3) 若该机器人搭载了 10 个机械手,它与采摘工人同时工作 1 h,假设工人 m s 可以采摘一个苹果,则机器人可比工人多采摘多少个苹果
用字母表示数量关系
(1) 一条河的水流速度是 2.5 km/h. 船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶的速度;
用含有字母的式子表示数量和数量关系的问题.
合作探究
顺水时
逆水时
船的速度=船在静水中的速度+水流速度
船的速度=船在静水中的速度-水流速度
行船问题
分析:
解:船在这条河中顺水行驶的速度是 (v+2.5) km/h,逆水行驶的速度是 (v-2.5) km/h.
书写规范
③后面带单位的相加或相减的式子要用括号括起来.
(2)一个正方形的边长是 a,这个正方形的周长 l 是多少?面积 S 呢
解:由正方形的周长=4×边长,
正方形的面积=边长×边长, 得
书写规范
④相同字母相乘时,结果需要写成幂的形式.
l=4a,
S=a2.
定义总结
想一想:这些式子都有什么样的特点?
它们都是用运算符号把数或表示数的字母连接起来的式子,
我们称这样的式子为代数式.
单独的一个数或字母也是代数式.
例如,5,t 都是代数式.
方法:(1) 代数式中不含表示数量关系的符号,如“=”“>”“<”“≥”“≤”“≠”等 .
(2) 单独的一个数或字母也是代数式.
例1 下列各式中哪些是代数式?哪些不是?
(1)m + 5 (2)a + b = b + a (3)0
(4)x + 3x + 4 (5)x + y>1 (6)
√
×
√
√
×
√
典例精析
典例精析
例2 (1) 苹果原价是 p 元/kg. 现在按九折优惠出售,用代数式表示苹果的售价:
解:现价是每千克 0.9p 元.
现价 = 原价×折扣 (0.9)
分析:
(2) 一个长方形的长是 0.9 m,宽是 p m. 用代数式表示这个长方形的面积;
解:长方形的面积为 0.9p m2.
(3) 某产品前年的产量是 n 件,去年的产量比前年产量的 2 倍少 10 件,用代数式表示去年的产量;
(4) 一个长方体水池底面的长和宽都是 a m,高是 h m, 池内水的体积占水池容积的三分之一,用代数式表示池内水的体积.
解:由长方体的体积=长×宽×高,得
这个长方体水池的容积是 a · a · h cm3,即 a2h cm3.
解:去年的产量是 ( 2n-10 ) 件.
故池内水的体积为 cm3.
练一练
1. (1) 某产品前年的产量是 n 件,去年的产量是前年产量的 m 倍,用代数式表示去年的产量;
解:去年的产量是 mn 件.
书写规范
⑤字母与字母相乘时,按字母表顺序排列.
(3) 用式子表示数 n 的相反数.
解:数 n 的相反数是-n.
书写规范
⑦ 当“1”与字母相乘时,“1”省略不写;
当“-1”与字母相乘时,只需在该字母前加上“-”号.
(2) 若每斤苹果 元,则买 m 斤苹果需 元.
书写规范
⑥带分数与字母相乘时,把带分数化成假分数.
想一想
知识点2:代数式的意义
在例 1 中“0.9p”代数式的意义是什么?
实际意义是什么?
实际意义:(1) 苹果的售价;(2) 长方形的面积.
总结
用字母表示数后,同一个代数式可以表示不同实际问题中的数量或数量关系.
代数式的意义:p 的 0.9 倍.
例2 说出下列代数式的意义:
典例精析
(1) 2a+3; (2) 2(a+3); (3) ; (4) x2+2x+8.
(4) x2+2x+8 的意义是 x 的平方,x 的 2 倍,与 8 的和.
解:(1) 2a+3 的意义是 a 的 2 倍与 3 的和;
(2) 2(a+3) 的意义是 a 与 3 的和的 2 倍;
(3) 的意义是 c 除以 a,b 的积的商;
变式 下列代数式可以表示什么实际意义呢?
(1)2a-b; (2)2(a-b).
解:(1)若篮球的单价是 a 元,足球的单价是 b 元,则 2a - b 可表示买两个篮球比买一个足球多花的钱数.
(2)若某商店的一台学习机的售价为 a 元,进价为 b 元,则 2(a - b) 可表示该商店卖出两台学习机的盈利.
答案不唯一.
想一想
字母表示数的含义:
数量
数量关系
计算公式
运算律
2n
s = vt
C = 2(a + b)
a+b = b+a
n只青蛙的眼睛的数量
s表示路程,v表示速度,t表示时间
长方形周长
加法交换律
仿照例子,你还能写出其他式子吗?
第肆章节
随堂练习
随堂练习
【教材P71】
1. 填空题.
(1)每包书有 10 册,6 包书有_____册,n 包书有______册;
(2)王芳今年 m 岁,她去年_______岁,6 年后________岁;
60
10n
(m-1)
(m+6)
(3)将 p kg 糖装入 n 个包装袋中,每袋糖的质量相同,每袋装入糖______kg;
(4)棱长为 a 的正方体的体积是_______.
p
n
a3
2. 说出下列代数式的意义:
(1)2a + 3c;(2)3(m-n);(3)a2 + 1;(4) .
3a
5b
解:(1)a 的 2 倍与 c 的 3 倍的和;
(2)m 与 n 的差的 3 倍;
(3)a 的平方与 1 的和;
(4)a 的 3 倍除以 b 的 5 倍的商.
3. 代数式 100-2x 可以表示不同实际问题中的数量或数量关系,请举例说明.
A、B 两地相距 100 km,一辆汽车以平均速度 x km/h,从 A 地出发,行驶 2 h后,距离 B 地还有(100-2x)千米.
第伍章节
课堂小结
课堂小结
代数式
代数式的定义
代数式的意义
代数式的书写要求
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
