5.3 第4课时 方案选择问题 课件 (共24张PPT)
文档属性
| 名称 | 5.3 第4课时 方案选择问题 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
人教版数学七年级上册
第五章 一元一次方程
汇报人:孙老师
汇报班级:X级X班
5.3实际问题与一元一次方程
5.3 第4课时 方案选择问题
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 会从空调的综合费用比较计费方式中寻找数量关系,列出方程.
2. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点分析问题,选择最优方案.
第贰章节
新课导入
新课导入
怎么选择更划算?
第叁章节
新知探究
新知探究
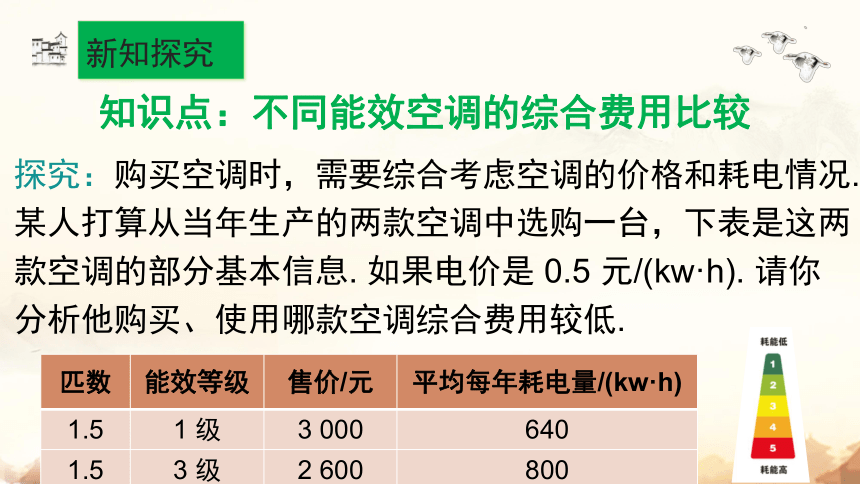
知识点:不同能效空调的综合费用比较
探究:购买空调时,需要综合考虑空调的价格和耗电情况. 某人打算从当年生产的两款空调中选购一台,下表是这两款空调的部分基本信息. 如果电价是 0.5 元/(kw·h). 请你分析他购买、使用哪款空调综合费用较低.
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
1 级
3 级
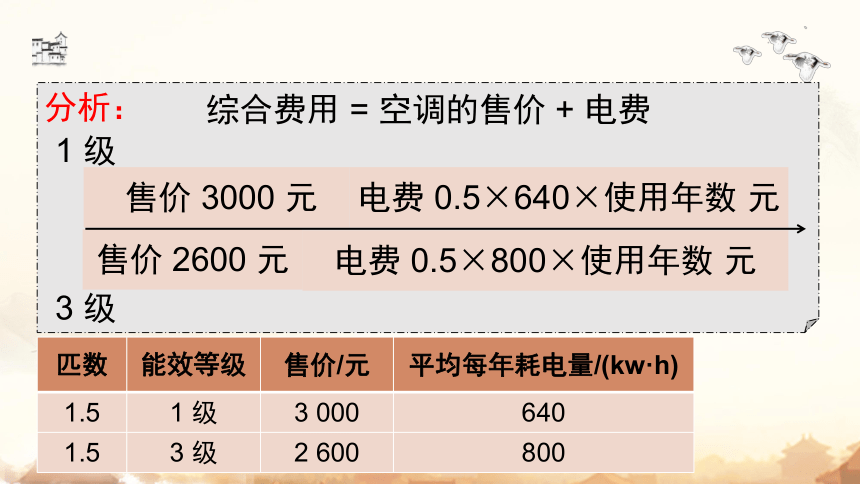
售价 3000 元
售价 2600 元
电费 0.5×640×使用年数 元
电费 0.5×800×使用年数 元
分析:
综合费用 = 空调的售价 + 电费
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
设空调的使用年数是 t,
则 1 级效能空调的综合费用 (单位:元) 是
3000 + 0.5×640t,
即 3000 + 320t
3 级效能空调的综合费用 (单位:元) 是
2600 + 0.5×800t,
即 2600 + 400t
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
问题1: t 取什么值时,两款空调的综合费用相等?
3000 + 320t = 2600 + 400t
解得 t = 5.
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
问题2:如何比较两款空调的综合费用?
比较 3000 + 320t 与 2600 + 400t 的大小.
方法一:运用整式的加减
(3000 + 320t) - (2600 + 400t)
= 3000 + 320t - 2600 - 400t
= 400 - 80t
= 80(5 - t)
当 t < 5 时,80(5 - t) > 0,
3000 + 320t > 2600 + 400t;
当 t > 5 时,80(5 - t) < 0,
3000 + 320t < 2600 + 400t.
(大数-小数>0,小数-大数<0)
方法二:把表示 3 级能效空调的综合资用的式子 2600 + 400t 变形为 1 级能效空调的综合费用与另外一个式于的和.
2600 + 400t = (3000 + 320t) + (80t - 400)
= (3000 + 320t) + 80(t - 5)
当 t < 5 时,80(5 - t) 是负数,
这表明 3 级能效空调的综合费用较低;
当 t > 5 时,80(5 - t) 是正数,
这表明 1 级能效空调的综合费用较低.
问题3:你认为哪种空调更划算呢?
同样是 1.5 匹的空调,1 级能效空调虽然售价高,但由于比较省电,使用年份长 (超过 5 年) 时综合费用反而低. 根据相关行业标准,空调的安全使用年限是 10 年 (从生产日期计起),因此购买、使用 1 级能效空调更划算.
当 t = 5 时,两款空调的综合费用相等;
当 t < 5 时,3 级能效空调的综合费用较低;
当 t > 5 时,1 级能效空调的综合费用较低.
1. 小翼打算办一张电话卡,有如下计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
设小翼主叫时间为 t,当 t≤150 时,选 划算;
当 时,两种方案计费相等;
方式一
当 时,选择方案二划算.
58 + 0.25(t - 150)
= 0.25t + 20.5
88 + 0.19(t - 350)
= 0.19t + 21.5
0.25t + 20.5 = 0.19t + 21.5
t = 270
t > 270
例1 某书店现推出如下购物优惠方案:
①一次性购书在 100 元 (不含 100 元) 以内,不享受优惠;
②一次性购书在 100 元 (含 100 元) 以上,350 元 (不含 350 元) 以内,一律享受九折优惠;
③一次性购书在 350 元 (含 350 元) 以上一律享八折优惠.
金额 (元) 小于 100 大于等于100小于350 大于等于350
优惠 无 0.9 0.8
小优原先计划两次购书分别付款 60 元和 288 元,现决定改为一次性付款,则应付款 元.
解:设第二次购书原本因花费 x 元.
② 第二次购物不低于 350 元
① 第二次购书超过 100 元,但不足 350 元
0.9x = 288
解得 x = 320.
0.8x = 288
解得 x = 360.
320 + 60 = 380
380×0.8 = 304 (元)
>350
360 + 60 = 420
420×0.8 = 336 (元)
>350
304 或 336
第肆章节
随堂练习
随堂练习
1. 在甲复印店用 A4 纸复印文件,复印页数不超过 20 时,每页收费 0.12 元;复印页数超过 20 时,超过部分每页收费降为 0.09 元,在乙复印店用 A4 纸复印文件,不论复印多少页,每页都收费 0.1 元,复印页数为多少时,两店的收费相同?
解:设复印页数为 x 时,两店的收费相同.
由题意可知,x > 20 .
根据题意,得 20×0.12 + (x-20)×0.09 = 0.1x .
解得 x = 60.
答:复印页数为 60 时,两店的收费相同.
2. 现有两种地铁机场线计次月票:第一种售价 200 元,每月包含 10 次;第二种售价 300 元,每月包含 20 次. 两种月票超出每月包含次数后都需要另外购票,票价
为25 元/次,某人每月乘坐地铁机场线超过 10 次,他购买哪种月票比较节省费用?
解:设他每月乘坐地铁机场线 x 次.
当 10 < x < 20 时,购买第一种月票需 [200 + 25(x - 10)] 元,
购买第二种月票需 300 元.
令 200 + 25(x - 10) = 300,解得 x = 14.
当 x ≥ 20 时,购买第二种月票比较节省费用.
因此,当他每月乘坐地铁机场线 14 次时,购买两种月票所需费用相同,超过 10 次且低于 14 次时,购买第一种月票
比较节省费用,超过 14 次时,购买第二种月票比较节省费用.
第伍章节
课堂小结
课堂小结
选择最优方案问题的一般步骤:
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学七年级上册
第五章 一元一次方程
汇报人:孙老师
汇报班级:X级X班
5.3实际问题与一元一次方程
5.3 第4课时 方案选择问题
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 会从空调的综合费用比较计费方式中寻找数量关系,列出方程.
2. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点分析问题,选择最优方案.
第贰章节
新课导入
新课导入
怎么选择更划算?
第叁章节
新知探究
新知探究
知识点:不同能效空调的综合费用比较
探究:购买空调时,需要综合考虑空调的价格和耗电情况. 某人打算从当年生产的两款空调中选购一台,下表是这两款空调的部分基本信息. 如果电价是 0.5 元/(kw·h). 请你分析他购买、使用哪款空调综合费用较低.
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
1 级
3 级
售价 3000 元
售价 2600 元
电费 0.5×640×使用年数 元
电费 0.5×800×使用年数 元
分析:
综合费用 = 空调的售价 + 电费
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
设空调的使用年数是 t,
则 1 级效能空调的综合费用 (单位:元) 是
3000 + 0.5×640t,
即 3000 + 320t
3 级效能空调的综合费用 (单位:元) 是
2600 + 0.5×800t,
即 2600 + 400t
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
问题1: t 取什么值时,两款空调的综合费用相等?
3000 + 320t = 2600 + 400t
解得 t = 5.
匹数 能效等级 售价/元 平均每年耗电量/(kw·h)
1.5 1 级 3 000 640
1.5 3 级 2 600 800
问题2:如何比较两款空调的综合费用?
比较 3000 + 320t 与 2600 + 400t 的大小.
方法一:运用整式的加减
(3000 + 320t) - (2600 + 400t)
= 3000 + 320t - 2600 - 400t
= 400 - 80t
= 80(5 - t)
当 t < 5 时,80(5 - t) > 0,
3000 + 320t > 2600 + 400t;
当 t > 5 时,80(5 - t) < 0,
3000 + 320t < 2600 + 400t.
(大数-小数>0,小数-大数<0)
方法二:把表示 3 级能效空调的综合资用的式子 2600 + 400t 变形为 1 级能效空调的综合费用与另外一个式于的和.
2600 + 400t = (3000 + 320t) + (80t - 400)
= (3000 + 320t) + 80(t - 5)
当 t < 5 时,80(5 - t) 是负数,
这表明 3 级能效空调的综合费用较低;
当 t > 5 时,80(5 - t) 是正数,
这表明 1 级能效空调的综合费用较低.
问题3:你认为哪种空调更划算呢?
同样是 1.5 匹的空调,1 级能效空调虽然售价高,但由于比较省电,使用年份长 (超过 5 年) 时综合费用反而低. 根据相关行业标准,空调的安全使用年限是 10 年 (从生产日期计起),因此购买、使用 1 级能效空调更划算.
当 t = 5 时,两款空调的综合费用相等;
当 t < 5 时,3 级能效空调的综合费用较低;
当 t > 5 时,1 级能效空调的综合费用较低.
1. 小翼打算办一张电话卡,有如下计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
设小翼主叫时间为 t,当 t≤150 时,选 划算;
当 时,两种方案计费相等;
方式一
当 时,选择方案二划算.
58 + 0.25(t - 150)
= 0.25t + 20.5
88 + 0.19(t - 350)
= 0.19t + 21.5
0.25t + 20.5 = 0.19t + 21.5
t = 270
t > 270
例1 某书店现推出如下购物优惠方案:
①一次性购书在 100 元 (不含 100 元) 以内,不享受优惠;
②一次性购书在 100 元 (含 100 元) 以上,350 元 (不含 350 元) 以内,一律享受九折优惠;
③一次性购书在 350 元 (含 350 元) 以上一律享八折优惠.
金额 (元) 小于 100 大于等于100小于350 大于等于350
优惠 无 0.9 0.8
小优原先计划两次购书分别付款 60 元和 288 元,现决定改为一次性付款,则应付款 元.
解:设第二次购书原本因花费 x 元.
② 第二次购物不低于 350 元
① 第二次购书超过 100 元,但不足 350 元
0.9x = 288
解得 x = 320.
0.8x = 288
解得 x = 360.
320 + 60 = 380
380×0.8 = 304 (元)
>350
360 + 60 = 420
420×0.8 = 336 (元)
>350
304 或 336
第肆章节
随堂练习
随堂练习
1. 在甲复印店用 A4 纸复印文件,复印页数不超过 20 时,每页收费 0.12 元;复印页数超过 20 时,超过部分每页收费降为 0.09 元,在乙复印店用 A4 纸复印文件,不论复印多少页,每页都收费 0.1 元,复印页数为多少时,两店的收费相同?
解:设复印页数为 x 时,两店的收费相同.
由题意可知,x > 20 .
根据题意,得 20×0.12 + (x-20)×0.09 = 0.1x .
解得 x = 60.
答:复印页数为 60 时,两店的收费相同.
2. 现有两种地铁机场线计次月票:第一种售价 200 元,每月包含 10 次;第二种售价 300 元,每月包含 20 次. 两种月票超出每月包含次数后都需要另外购票,票价
为25 元/次,某人每月乘坐地铁机场线超过 10 次,他购买哪种月票比较节省费用?
解:设他每月乘坐地铁机场线 x 次.
当 10 < x < 20 时,购买第一种月票需 [200 + 25(x - 10)] 元,
购买第二种月票需 300 元.
令 200 + 25(x - 10) = 300,解得 x = 14.
当 x ≥ 20 时,购买第二种月票比较节省费用.
因此,当他每月乘坐地铁机场线 14 次时,购买两种月票所需费用相同,超过 10 次且低于 14 次时,购买第一种月票
比较节省费用,超过 14 次时,购买第二种月票比较节省费用.
第伍章节
课堂小结
课堂小结
选择最优方案问题的一般步骤:
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
