6.2.2 线段长短的比较与运算 课件(共36张PPT)
文档属性
| 名称 | 6.2.2 线段长短的比较与运算 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 15:05:54 | ||
图片预览








文档简介
(共36张PPT)
人教版数学七年级上册
第六章 几何图形初步
汇报人:孙老师
汇报班级:X级X班
6.2 直线、射线、线段
6.2.2 线段长短的比较与运算
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义.能够运用线段的和、差、倍、分关系求线段的长度.
3. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
第贰章节
新课导入
新课导入
1.基本事实:
经过两点有一条直线,并且只有一条直线.
简单说成:___________________
两点确定一条直线
A
B
A
B
l
A
B
a
A
B
l
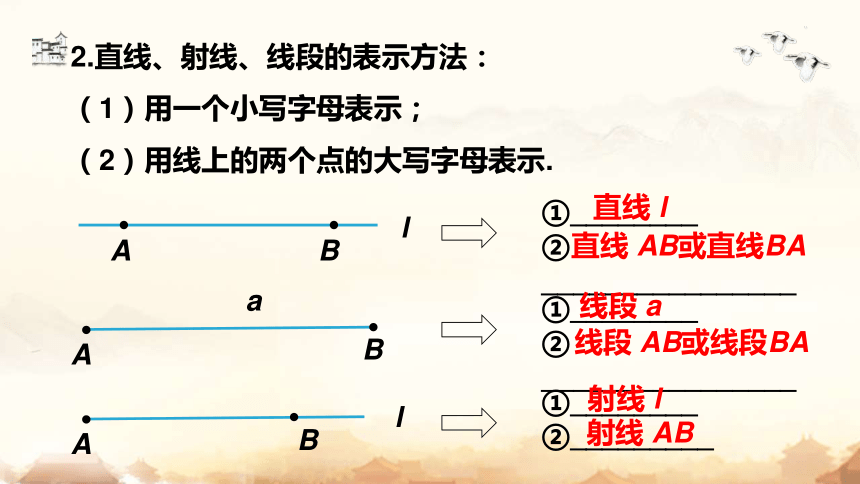
2.直线、射线、线段的表示方法:
(1)用一个小写字母表示;
(2)用线上的两个点的大写字母表示.
①________
②________________
①________
②________________
①________
②_________
直线 l
直线 AB或直线BA
线段 a
线段 AB或线段BA
射线 l
射线 AB
第叁章节
新知探究
新知探究
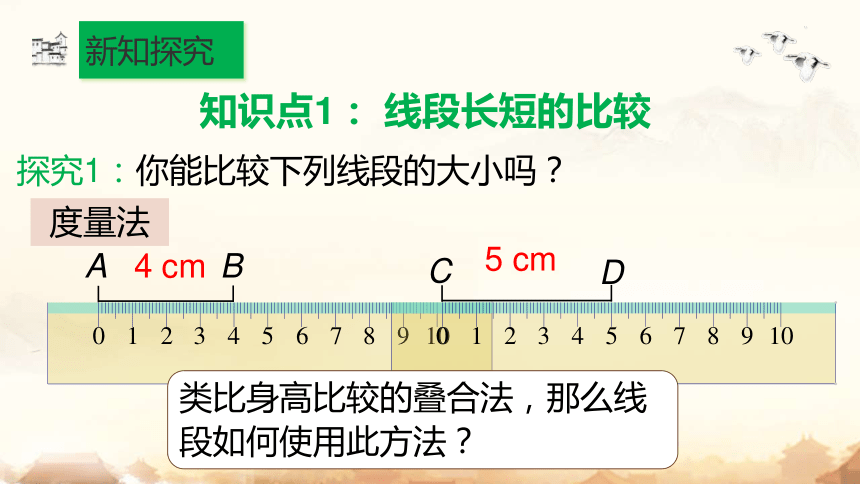
知识点1: 线段长短的比较
探究1:你能比较下列线段的大小吗?
度量法
4 cm
5 cm
类比身高比较的叠合法,那么线段如何使用此方法?
A
B
C
D
1. 两条线段要放在同一条直线上.
2. 一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
合作探究
合作探究
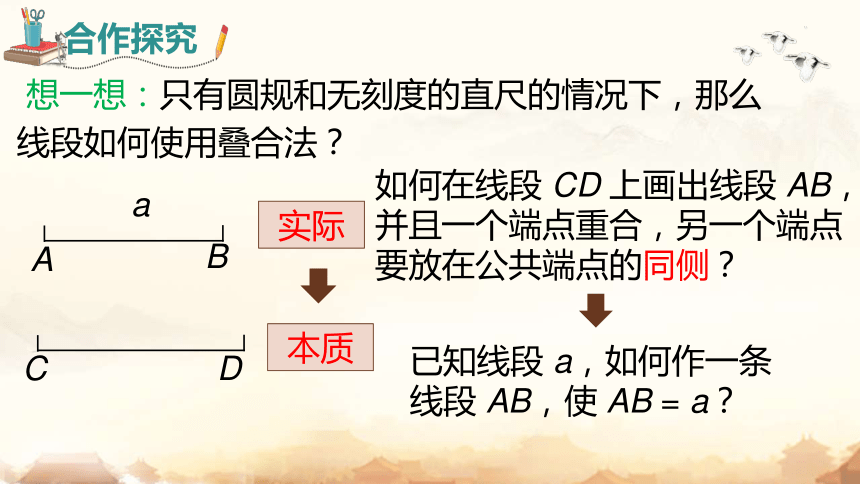
想一想:只有圆规和无刻度的直尺的情况下,那么线段如何使用叠合法?
A
B
C
D
如何在线段 CD 上画出线段 AB,
并且一个端点重合,另一个端点要放在公共端点的同侧?
已知线段 a,如何作一条线段 AB,使 AB = a?
实际
本质
a
总结
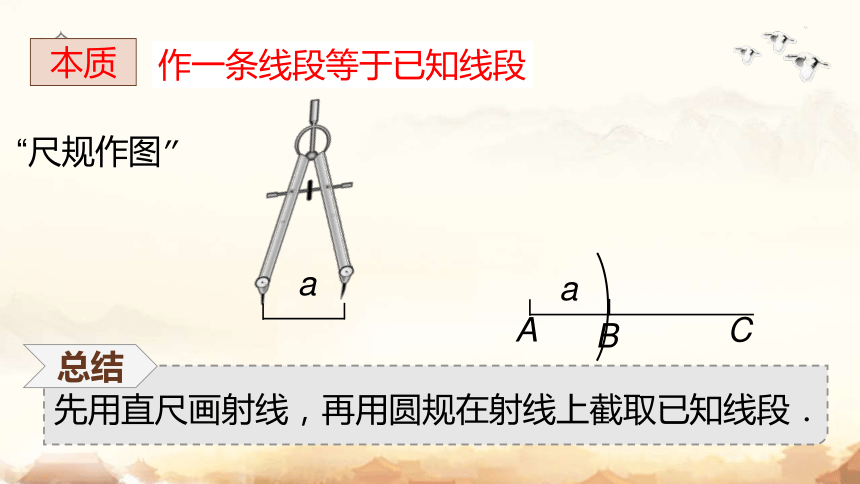
“尺规作图”
先用直尺画射线,再用圆规在射线上截取已知线段.
a
B
作一条线段等于已知线段
a
A
C
本质
叠合法
A
B
C
D
如何在线段 CD 上画出线段 AB,并且一端端点重合,另一个端点要放在公共端点的同侧?
实际
(A)
B
归纳总结
叠合法比较线段的大小:
A(C)
D
B
AB>CD
AB = CD
AB<CD
A(C)
D
B
A(C)
B(D)
画一画
1.在一条直线上,画出线段 AB = 6 cm, BC = 4 cm.
A
C
B
6 cm
4 cm
A
C
B
6 cm
4 cm
知识点2: 有关线段的基本事实
如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
归纳总结
经过比较,我们可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
连接两点的线段的长度,叫作
这两点的距离.
简单说成:两点之间,线段最短.
A
B
两点之间,线段最短
1. 如图,这是 A,B 两地之间的公路,在公路工程
改造计划时,为使 A,B 两地行程最短,应如何
设计线路?请在图中画出,并说明理由.
.
B
A
.
生活实例
知识点3: 线段的和、差、倍、分
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
画一画
2.如图,已知线段 a,求作线段 AB=2a.
a
M
B
a
A
P
AB = 2a
a
总结
如图,点 M 把线段 AB 分成相等的两条线段 AM 与 BM,点 M 叫作线段 AB 的中点.
A
a
a
M
B
M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM).
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点.
思考 那么什么叫作三等分点?四等分点呢?
三等分点
如图,若点 M、N 是线段 AB 的三等分点,
则 AM = = = ,反过来也成立.
MN
NB
AB
1
3
四等分点
如图,若点 M、N、P 是线段 AB 的四等分点,
则 AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
典例精析
例1 (成都期末) 如图,长度为 20 cm 的线段 AB 的中点为 M,点 C 在线段 MB 上,且 MC∶CB = 2∶3,则线段 AC 的长度为_______cm.
A
C
B
M
分析:由题意得
MC∶CB = 2∶3
AC = AM + CM = 14 cm
CM = BM = 4 cm
AM = BM = AB = 10 cm
14
第肆章节
随堂练习
随堂练习
1.下列说法正确的是( )
A.连接两点的线段叫作两点间的距离
B.两点间连线的长度,叫作两点间的距离
C.连接两点的直线的长度,叫作两点的距离
D.连接两点间的线段的长度,叫作两点间的距离
D
2.下列说法正确的是( )
A.画一条3cm长的直线
B.画一条3cm长的射线
C.画一条3cm长的线段
D.在直线、射线、线段中直线最长.
C
3. 若AB=4 cm,BC=3 cm,则A,C 两点的距离为( )
A.1 cm B.7 cm
C.1 cm或7 cm D.不确定
D
【选自教材P166 练习 第1题】
4. 估计下列图中线段AB与AC的大小关系,再用刻度尺或圆规检验.
AB>AC
AB<AC
AB=AC
5.如图,已知线段 a,b,求作线段 AB,使得 AB =a+2b.小明给出了四个步骤:①在射线 AM 上截取线段AP=a;②则线段 AB=a+2b;③在射线 PM 上截取 PQ =b,QB=b;④画射线 AM.你认为正确的顺序是( )
A.①②③④
B.④①③②
C.④③①②
D.④②①③
B
6.如图,C为线段 AB 的中点,D 是线段 BC 的中点,若BD =4 cm,则AB=______cm.
16
7.如图,已知线段a,b,作一条线段,使它等于a+2b.
解:如图所示.
【选自教材P166 练习 第2题】
解:当点 P在线段 MN 的延长线上时,如图①,MP=MN+NP=3+1=4(cm);
当点P在线段MN上时,如图②,MP=MN-NP=3-1=2(cm).
综上所述,线段 MP 的长为 4 cm 或2 cm.
8.点M,N,P,在同一直线上,MN=3cm,NP=1cm.求线段MP的长.
【选自教材P166 练习 第3题】
第伍章节
课堂小结
课堂小结
线段
尺规作图
比较长短的方法
基本事实
两点的距离
线段的中点
作一条线段等于已知线段
作线段的和差
度量法
叠合法
两点之间,线段最短
把一条线段分成两条相等线段的点
连接两点间的线段的长度
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学七年级上册
第六章 几何图形初步
汇报人:孙老师
汇报班级:X级X班
6.2 直线、射线、线段
6.2.2 线段长短的比较与运算
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义.能够运用线段的和、差、倍、分关系求线段的长度.
3. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
第贰章节
新课导入
新课导入
1.基本事实:
经过两点有一条直线,并且只有一条直线.
简单说成:___________________
两点确定一条直线
A
B
A
B
l
A
B
a
A
B
l
2.直线、射线、线段的表示方法:
(1)用一个小写字母表示;
(2)用线上的两个点的大写字母表示.
①________
②________________
①________
②________________
①________
②_________
直线 l
直线 AB或直线BA
线段 a
线段 AB或线段BA
射线 l
射线 AB
第叁章节
新知探究
新知探究
知识点1: 线段长短的比较
探究1:你能比较下列线段的大小吗?
度量法
4 cm
5 cm
类比身高比较的叠合法,那么线段如何使用此方法?
A
B
C
D
1. 两条线段要放在同一条直线上.
2. 一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
合作探究
合作探究
想一想:只有圆规和无刻度的直尺的情况下,那么线段如何使用叠合法?
A
B
C
D
如何在线段 CD 上画出线段 AB,
并且一个端点重合,另一个端点要放在公共端点的同侧?
已知线段 a,如何作一条线段 AB,使 AB = a?
实际
本质
a
总结
“尺规作图”
先用直尺画射线,再用圆规在射线上截取已知线段.
a
B
作一条线段等于已知线段
a
A
C
本质
叠合法
A
B
C
D
如何在线段 CD 上画出线段 AB,并且一端端点重合,另一个端点要放在公共端点的同侧?
实际
(A)
B
归纳总结
叠合法比较线段的大小:
A(C)
D
B
AB>CD
AB = CD
AB<CD
A(C)
D
B
A(C)
B(D)
画一画
1.在一条直线上,画出线段 AB = 6 cm, BC = 4 cm.
A
C
B
6 cm
4 cm
A
C
B
6 cm
4 cm
知识点2: 有关线段的基本事实
如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
归纳总结
经过比较,我们可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
连接两点的线段的长度,叫作
这两点的距离.
简单说成:两点之间,线段最短.
A
B
两点之间,线段最短
1. 如图,这是 A,B 两地之间的公路,在公路工程
改造计划时,为使 A,B 两地行程最短,应如何
设计线路?请在图中画出,并说明理由.
.
B
A
.
生活实例
知识点3: 线段的和、差、倍、分
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
画一画
2.如图,已知线段 a,求作线段 AB=2a.
a
M
B
a
A
P
AB = 2a
a
总结
如图,点 M 把线段 AB 分成相等的两条线段 AM 与 BM,点 M 叫作线段 AB 的中点.
A
a
a
M
B
M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM).
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点.
思考 那么什么叫作三等分点?四等分点呢?
三等分点
如图,若点 M、N 是线段 AB 的三等分点,
则 AM = = = ,反过来也成立.
MN
NB
AB
1
3
四等分点
如图,若点 M、N、P 是线段 AB 的四等分点,
则 AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
典例精析
例1 (成都期末) 如图,长度为 20 cm 的线段 AB 的中点为 M,点 C 在线段 MB 上,且 MC∶CB = 2∶3,则线段 AC 的长度为_______cm.
A
C
B
M
分析:由题意得
MC∶CB = 2∶3
AC = AM + CM = 14 cm
CM = BM = 4 cm
AM = BM = AB = 10 cm
14
第肆章节
随堂练习
随堂练习
1.下列说法正确的是( )
A.连接两点的线段叫作两点间的距离
B.两点间连线的长度,叫作两点间的距离
C.连接两点的直线的长度,叫作两点的距离
D.连接两点间的线段的长度,叫作两点间的距离
D
2.下列说法正确的是( )
A.画一条3cm长的直线
B.画一条3cm长的射线
C.画一条3cm长的线段
D.在直线、射线、线段中直线最长.
C
3. 若AB=4 cm,BC=3 cm,则A,C 两点的距离为( )
A.1 cm B.7 cm
C.1 cm或7 cm D.不确定
D
【选自教材P166 练习 第1题】
4. 估计下列图中线段AB与AC的大小关系,再用刻度尺或圆规检验.
AB>AC
AB<AC
AB=AC
5.如图,已知线段 a,b,求作线段 AB,使得 AB =a+2b.小明给出了四个步骤:①在射线 AM 上截取线段AP=a;②则线段 AB=a+2b;③在射线 PM 上截取 PQ =b,QB=b;④画射线 AM.你认为正确的顺序是( )
A.①②③④
B.④①③②
C.④③①②
D.④②①③
B
6.如图,C为线段 AB 的中点,D 是线段 BC 的中点,若BD =4 cm,则AB=______cm.
16
7.如图,已知线段a,b,作一条线段,使它等于a+2b.
解:如图所示.
【选自教材P166 练习 第2题】
解:当点 P在线段 MN 的延长线上时,如图①,MP=MN+NP=3+1=4(cm);
当点P在线段MN上时,如图②,MP=MN-NP=3-1=2(cm).
综上所述,线段 MP 的长为 4 cm 或2 cm.
8.点M,N,P,在同一直线上,MN=3cm,NP=1cm.求线段MP的长.
【选自教材P166 练习 第3题】
第伍章节
课堂小结
课堂小结
线段
尺规作图
比较长短的方法
基本事实
两点的距离
线段的中点
作一条线段等于已知线段
作线段的和差
度量法
叠合法
两点之间,线段最短
把一条线段分成两条相等线段的点
连接两点间的线段的长度
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
