6.3.3 余角和补角 课件(共28张PPT)
文档属性
| 名称 | 6.3.3 余角和补角 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 14:54:18 | ||
图片预览








文档简介
(共28张PPT)
人教版数学七年级上册
第六章 几何图形初步
汇报人:孙老师
汇报班级:X级X班
6.3 角
6.3.3 余角和补角
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 掌握余角和补角的性质,能运用余角与补角的性质解决实际问题.
2. 通过余角、补角的性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.
第贰章节
新课导入
新课导入
O
A
C
B
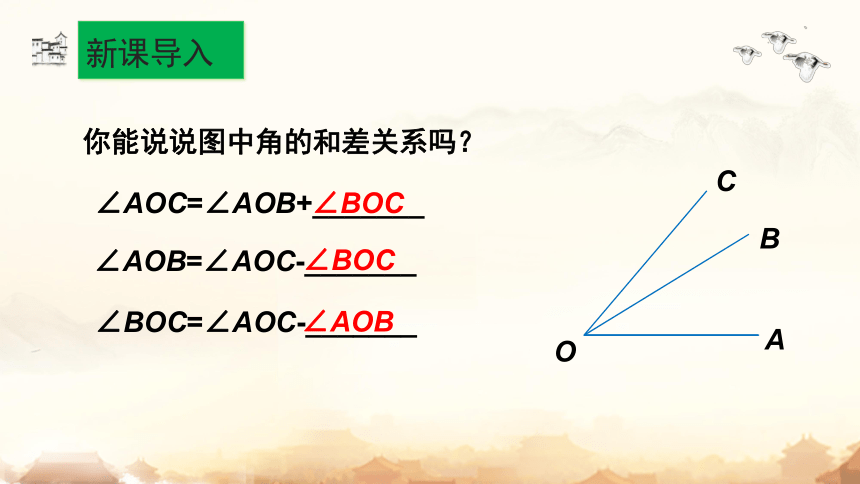
你能说说图中角的和差关系吗?
∠AOC=∠AOB+_______
∠AOB=∠AOC-_______
∠BOC=∠AOC-_______
∠BOC
∠BOC
∠AOB
第叁章节
新知探究
新知探究
知识点1:余角
余角:
如果两个角的和等于 90° (直角),就说这两个角互为余角,简称这两个角互余.
∠3 与∠4 互余;
∠3 是∠4 的余角;
∠4 是∠3 的余角.
3
4
∠3 与∠4 依然互余.
讨论1:此时∠3 与∠4 还互余吗?
讨论2:钝角有余角吗?
没有.
总结
角的数量关系与位置无关.
总结
只有锐角有余角.
3
4
几何语言:
因为∠3 与∠4 互余,
所以 ∠3 +∠4 = 90°
或 ∠3 = 90° -∠4
或 ∠4 = 90° -∠3.
因为∠3 +∠4 = 90°,
所以∠3 与∠4 互余.
互余定义
3
4
补角:
知识要点
如果两个角的和等于 180° (平角),就说这两个角互为补角,简称这两个角互补.
探究1:你能猜猜∠1 与∠2 的数量关系吗?
1
2
知识点2:补角
几何语言:
1
2
因为∠1 与∠2 互补,
所以 ∠1 +∠2 = 180°
或 ∠1 = 180° -∠2
或 ∠2 = 180° -∠1.
因为∠1 + ∠2 = 180°,
所以∠1 与∠2 互补.
互补定义
判断:下列论述是否正确?
①∠1 +∠2 +∠3 = 90°,则∠1、∠2、∠3互余;
②∠1 = 20°,∠2 = 100°,∠3 = 180°,则∠1、∠2、∠3 互补;
③∠1 +∠2 = 90°,则∠1 是余角;∠3 +∠4 = 180°,则∠3 是∠4 的补角;
④如图,∠A 不是∠B 的余角;
⑤如图,∠C 是∠A 的补角.
×
×
×
×
两个角之间的关系
√
32°
A
58°
B
148°
C
比一比:看看谁计算得又快又好!
∠α 5° 62°23′ x° (0余角 60°
补角 110°
∠α 是锐角,则它的余角可以表示为 ,
补角可以表示为 .
90° -∠α
180° -∠α
85°
175°
27°37′
117°37′
(90 - x)°
(180 - x)°
(70 + x)°
(110 + x)°
30°
150°
70°
20°
知识点3:余角与补角的性质
探究2:∠1 与∠2,∠3 都互为补角,∠2 与∠3 的大小有什么关系?
因为∠1 与∠2,∠3 都互为补角,
所以∠2 = 180° - ∠1,∠3 = 180° - ∠1.
所以∠2 =∠3.
补角的性质:
知识要点
同角 (等角) 的补角相等.
探究3:类比探究 2,∠1 与∠2,∠3 都互为余角,∠2 与∠3 的大小有什么关系?
因为∠1 与∠2,∠3 都互为余角,
所以∠2 = 90° - ∠1,∠3 = 90° - ∠1.
所以∠2 = ∠3 .
余角的性质:
定义总结
同角 (等角) 的余角相等.
例1 如图,点 A,O,B 在同一条直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
典例精讲
解:因为点 A,O,B 在同一条直线上,
所以∠AOC 和∠BOC 互为补角.
A
O
B
C
D
E
补角的定义
A
O
B
C
D
E
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,
所以∠COD +∠COE = ∠AOC + ∠BOC
= (∠AOC +∠BOC )
= 90°
所以∠COD 和∠COE 互为余角,
同理,∠AOD 和∠BOE,∠AOD 和∠COE,∠COD 和∠BOE 互为余角.
等式的性质
余角的定义
第肆章节
随堂练习
随堂练习
1.∠1与∠2互为补角,且∠1>∠2,则∠2 的余角是( )
A.∠1+∠2 B.∠1-∠2
C.∠1-90° D.90°-∠1
C
2.如图,O为直线 AB 上一点,OD 平分∠AOC,∠DOE=90°.
(1)图中共有_____对互补的角;
(2)若∠AOD=50°,求∠BOC 的度数.
5
(2)解:因为OD平分∠AOC,∠AOD=50°
所以∠AOC=2∠AOD=100°,
所以∠BOC=180-∠AOC=80°.
3.图中给出的各角中,哪些互为余角?哪些互为补角?
【选自教材P177 练习 第1题】
解:互为余角的角是 10°和 80°、30°和 60°,互为补角的角是10°和 170°、30°和 150°、60°和 120°、80°和 100°.
【选自教材P177 练习 第2题】
4. 一个角是70°39',求它的余角和补角.
解:它的余角是 19°21′,补角是 109°21′.
5. ∠α的补角是它的3倍,∠α是多少度?
解:设∠α= x.则 3x=180°-x,解得 x=45°.所以∠α是 45°
【选自教材P177 练习 第3题】
6.如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进入围墙,如何测量?
解:先将其一边 OA 反向延长为 OC,便可测出∠BOC 的度数,而∠AOB与∠BOC互为补角,故∠AOB=180°-∠BOC
C
【选自教材P177 练习 第4题】
第伍章节
课堂小结
课堂小结
余角和补角
余角和补角的性质:
互余和互补:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.其中一个角是另一个角的余角.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.其中一个角是另一个角的补角.
1.同角(等角)的余角相等.
2.同角(等角)的补角相等.
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学七年级上册
第六章 几何图形初步
汇报人:孙老师
汇报班级:X级X班
6.3 角
6.3.3 余角和补角
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 掌握余角和补角的性质,能运用余角与补角的性质解决实际问题.
2. 通过余角、补角的性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.
第贰章节
新课导入
新课导入
O
A
C
B
你能说说图中角的和差关系吗?
∠AOC=∠AOB+_______
∠AOB=∠AOC-_______
∠BOC=∠AOC-_______
∠BOC
∠BOC
∠AOB
第叁章节
新知探究
新知探究
知识点1:余角
余角:
如果两个角的和等于 90° (直角),就说这两个角互为余角,简称这两个角互余.
∠3 与∠4 互余;
∠3 是∠4 的余角;
∠4 是∠3 的余角.
3
4
∠3 与∠4 依然互余.
讨论1:此时∠3 与∠4 还互余吗?
讨论2:钝角有余角吗?
没有.
总结
角的数量关系与位置无关.
总结
只有锐角有余角.
3
4
几何语言:
因为∠3 与∠4 互余,
所以 ∠3 +∠4 = 90°
或 ∠3 = 90° -∠4
或 ∠4 = 90° -∠3.
因为∠3 +∠4 = 90°,
所以∠3 与∠4 互余.
互余定义
3
4
补角:
知识要点
如果两个角的和等于 180° (平角),就说这两个角互为补角,简称这两个角互补.
探究1:你能猜猜∠1 与∠2 的数量关系吗?
1
2
知识点2:补角
几何语言:
1
2
因为∠1 与∠2 互补,
所以 ∠1 +∠2 = 180°
或 ∠1 = 180° -∠2
或 ∠2 = 180° -∠1.
因为∠1 + ∠2 = 180°,
所以∠1 与∠2 互补.
互补定义
判断:下列论述是否正确?
①∠1 +∠2 +∠3 = 90°,则∠1、∠2、∠3互余;
②∠1 = 20°,∠2 = 100°,∠3 = 180°,则∠1、∠2、∠3 互补;
③∠1 +∠2 = 90°,则∠1 是余角;∠3 +∠4 = 180°,则∠3 是∠4 的补角;
④如图,∠A 不是∠B 的余角;
⑤如图,∠C 是∠A 的补角.
×
×
×
×
两个角之间的关系
√
32°
A
58°
B
148°
C
比一比:看看谁计算得又快又好!
∠α 5° 62°23′ x° (0
补角 110°
∠α 是锐角,则它的余角可以表示为 ,
补角可以表示为 .
90° -∠α
180° -∠α
85°
175°
27°37′
117°37′
(90 - x)°
(180 - x)°
(70 + x)°
(110 + x)°
30°
150°
70°
20°
知识点3:余角与补角的性质
探究2:∠1 与∠2,∠3 都互为补角,∠2 与∠3 的大小有什么关系?
因为∠1 与∠2,∠3 都互为补角,
所以∠2 = 180° - ∠1,∠3 = 180° - ∠1.
所以∠2 =∠3.
补角的性质:
知识要点
同角 (等角) 的补角相等.
探究3:类比探究 2,∠1 与∠2,∠3 都互为余角,∠2 与∠3 的大小有什么关系?
因为∠1 与∠2,∠3 都互为余角,
所以∠2 = 90° - ∠1,∠3 = 90° - ∠1.
所以∠2 = ∠3 .
余角的性质:
定义总结
同角 (等角) 的余角相等.
例1 如图,点 A,O,B 在同一条直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
典例精讲
解:因为点 A,O,B 在同一条直线上,
所以∠AOC 和∠BOC 互为补角.
A
O
B
C
D
E
补角的定义
A
O
B
C
D
E
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,
所以∠COD +∠COE = ∠AOC + ∠BOC
= (∠AOC +∠BOC )
= 90°
所以∠COD 和∠COE 互为余角,
同理,∠AOD 和∠BOE,∠AOD 和∠COE,∠COD 和∠BOE 互为余角.
等式的性质
余角的定义
第肆章节
随堂练习
随堂练习
1.∠1与∠2互为补角,且∠1>∠2,则∠2 的余角是( )
A.∠1+∠2 B.∠1-∠2
C.∠1-90° D.90°-∠1
C
2.如图,O为直线 AB 上一点,OD 平分∠AOC,∠DOE=90°.
(1)图中共有_____对互补的角;
(2)若∠AOD=50°,求∠BOC 的度数.
5
(2)解:因为OD平分∠AOC,∠AOD=50°
所以∠AOC=2∠AOD=100°,
所以∠BOC=180-∠AOC=80°.
3.图中给出的各角中,哪些互为余角?哪些互为补角?
【选自教材P177 练习 第1题】
解:互为余角的角是 10°和 80°、30°和 60°,互为补角的角是10°和 170°、30°和 150°、60°和 120°、80°和 100°.
【选自教材P177 练习 第2题】
4. 一个角是70°39',求它的余角和补角.
解:它的余角是 19°21′,补角是 109°21′.
5. ∠α的补角是它的3倍,∠α是多少度?
解:设∠α= x.则 3x=180°-x,解得 x=45°.所以∠α是 45°
【选自教材P177 练习 第3题】
6.如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进入围墙,如何测量?
解:先将其一边 OA 反向延长为 OC,便可测出∠BOC 的度数,而∠AOB与∠BOC互为补角,故∠AOB=180°-∠BOC
C
【选自教材P177 练习 第4题】
第伍章节
课堂小结
课堂小结
余角和补角
余角和补角的性质:
互余和互补:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.其中一个角是另一个角的余角.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.其中一个角是另一个角的补角.
1.同角(等角)的余角相等.
2.同角(等角)的补角相等.
人教版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
