6.4 多边形的内角和课件(15张PPT) 北师大版八年级下册
文档属性
| 名称 | 6.4 多边形的内角和课件(15张PPT) 北师大版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 14:10:04 | ||
图片预览




文档简介
(共15张PPT)
6.4.1 多边形的内角和
第六章 平行四边形
思考:你知道这些多边形的内角和是多少吗?
探究新知1
探索四边形的内角和
四边形的内角和是360°
问题1:你能用以前学过的知识说明一下你的结论吗?
活动实践:1、请在你的练习本上画一个任意的四边形。
2、用自己的方法探索四边形的内角和,可以借助
工具。
3、限时4分钟。
猜想与证明:
1
多边形的内角和
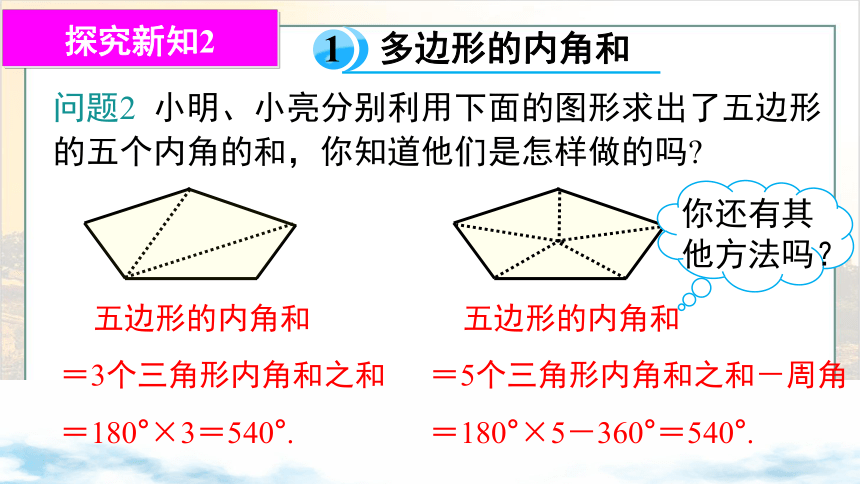
问题2 小明、小亮分别利用下面的图形求出了五边形的五个内角的和,你知道他们是怎样做的吗
五边形的内角和
=3个三角形内角和之和
=180°×3=540°.
五边形的内角和
=5个三角形内角和之和-周角
=180°×5-360°=540°.
你还有其他方法吗?
探究新知2
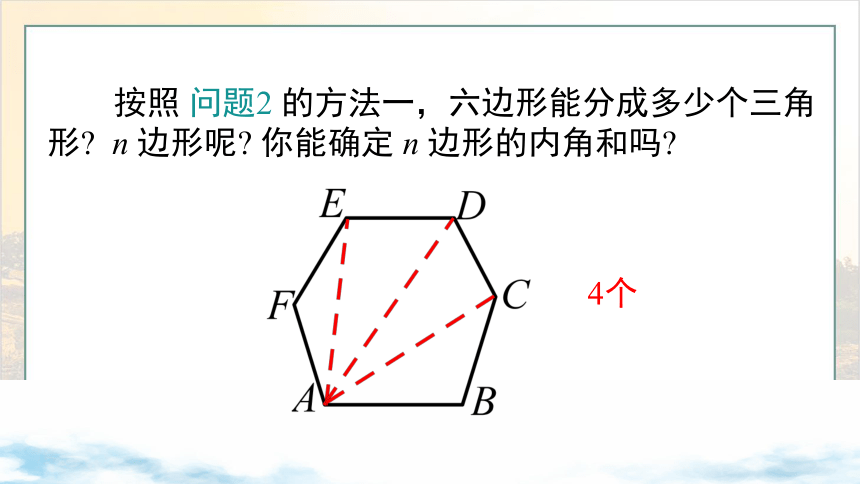
按照 问题2 的方法一,六边形能分成多少个三角形 n 边形呢 你能确定 n 边形的内角和吗
4个
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
···
0
n - 3
1
2
3
1
2
3
4
n - 2
(n - 2)×180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
······
···
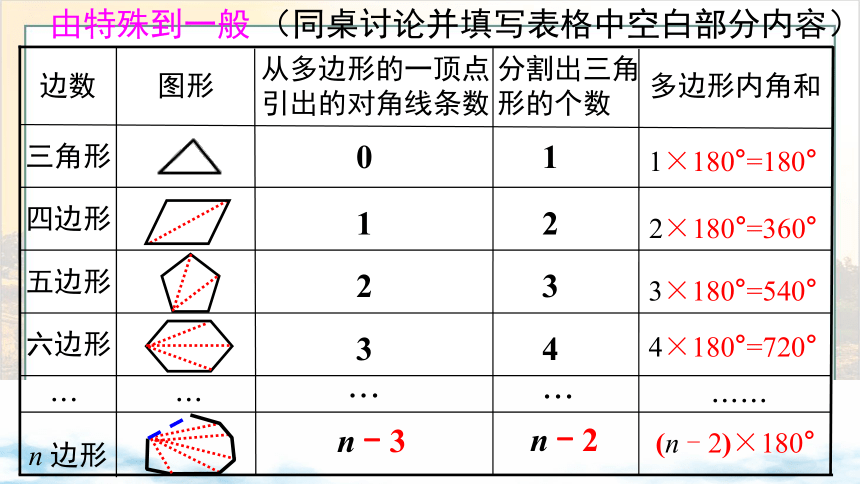
由特殊到一般 (同桌讨论并填写表格中空白部分内容)
定理 n 边形的内角和等于 (n - 2)×180°
( n 是大于或等于 3 的自然数).
按照 问题2 的方法二再试一试?
多边形的内角和公式
总结归纳
从多边形的一个顶点可以引出(n-3) 条对角线,把n边形分成(n-2)个三角形
例1 在四边形 ABCD 中,∠A +∠C = 180°,那么 ∠B 与 ∠D 有什么关系?
B
A
D
C
如果一个四边形的一组对角互补,那么另一组对角互补.
解:∵∠A +∠B +∠C +∠D
= (4 - 2)×180° = 360°,
∴∠B +∠D
= 360°-(∠A +∠C) = 180°.
典例精析
想一想:正 n 边形的一个内角是 度.
正三角形 (等边三角形) 、正四边形 (正方形) 、正五边形、正六边形、正八边形的内角分别是多少度
60°
108°
90°
120°
135°
想一想
剪掉一张长方形纸片的一个角后,纸片还剩几个角 这个多边形的内角和是多少度 与同伴交流.
540°
360°
180°
(小组合作)
议一议
随堂练习
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90°
C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是( )
A.9 B.8
C.7 D.6
A
B
3.六边形的内角和等于( )°.
4.正十边形的每一个内角的度数等于( )°.
5.一个多边形从一个顶点出发有4条对角线,则这个多边形的内角和为( )°.
720
144
900
3. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
头脑风暴
谈谈你在这节课中,有什么收获?
课堂小结
6.4.1 多边形的内角和
第六章 平行四边形
思考:你知道这些多边形的内角和是多少吗?
探究新知1
探索四边形的内角和
四边形的内角和是360°
问题1:你能用以前学过的知识说明一下你的结论吗?
活动实践:1、请在你的练习本上画一个任意的四边形。
2、用自己的方法探索四边形的内角和,可以借助
工具。
3、限时4分钟。
猜想与证明:
1
多边形的内角和
问题2 小明、小亮分别利用下面的图形求出了五边形的五个内角的和,你知道他们是怎样做的吗
五边形的内角和
=3个三角形内角和之和
=180°×3=540°.
五边形的内角和
=5个三角形内角和之和-周角
=180°×5-360°=540°.
你还有其他方法吗?
探究新知2
按照 问题2 的方法一,六边形能分成多少个三角形 n 边形呢 你能确定 n 边形的内角和吗
4个
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
···
0
n - 3
1
2
3
1
2
3
4
n - 2
(n - 2)×180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
······
···
由特殊到一般 (同桌讨论并填写表格中空白部分内容)
定理 n 边形的内角和等于 (n - 2)×180°
( n 是大于或等于 3 的自然数).
按照 问题2 的方法二再试一试?
多边形的内角和公式
总结归纳
从多边形的一个顶点可以引出(n-3) 条对角线,把n边形分成(n-2)个三角形
例1 在四边形 ABCD 中,∠A +∠C = 180°,那么 ∠B 与 ∠D 有什么关系?
B
A
D
C
如果一个四边形的一组对角互补,那么另一组对角互补.
解:∵∠A +∠B +∠C +∠D
= (4 - 2)×180° = 360°,
∴∠B +∠D
= 360°-(∠A +∠C) = 180°.
典例精析
想一想:正 n 边形的一个内角是 度.
正三角形 (等边三角形) 、正四边形 (正方形) 、正五边形、正六边形、正八边形的内角分别是多少度
60°
108°
90°
120°
135°
想一想
剪掉一张长方形纸片的一个角后,纸片还剩几个角 这个多边形的内角和是多少度 与同伴交流.
540°
360°
180°
(小组合作)
议一议
随堂练习
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90°
C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是( )
A.9 B.8
C.7 D.6
A
B
3.六边形的内角和等于( )°.
4.正十边形的每一个内角的度数等于( )°.
5.一个多边形从一个顶点出发有4条对角线,则这个多边形的内角和为( )°.
720
144
900
3. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
头脑风暴
谈谈你在这节课中,有什么收获?
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
