【小升初押题卷】广东省2024-2025学年重点中学小升初择校分班考前冲刺预测卷人教版(含解析)
文档属性
| 名称 | 【小升初押题卷】广东省2024-2025学年重点中学小升初择校分班考前冲刺预测卷人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 296.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年重点中学小升初择校分班考前冲刺预测卷人教版
一、选择题
1.下面各数能用百分数表示的是( )。
A.一辆货车载重约吨 B.大米比面粉多千克
C.一根绳子长米 D.一根绳子,用去了
2.把5克盐溶在50克水中,盐与盐水的质量比是( )。
A. B. C. D.
3.一个圆有( )直径。
A.1条 B.2条 C.无数条 D.0条
4.一种微型零件,零件实际长度是8毫米,而画到纸上是8分米,这幅图的比例尺是( )
A.1∶100 B.100∶1 C.1∶1000 D.1000∶1
5.乐乐向北走40米,记作﹣40米,那么他向南走100米,记作( )。
A.﹣100米 B.﹢100米 C.﹣140米 D.140米
6.若a是非零的自然数,下列算式中的计算结果最大的是( )。
A.a× B.a÷ C.a÷ D.÷a
7.甲、乙二人从底楼(第一层)开始比赛爬楼梯(每两层之间楼梯的级数相同)甲跑到第4层时,乙恰好到第3层,照这样的速度,甲跑到第16层时,乙跑到( )层。
A.9 B.10 C.11 D.12
二、填空题
8.在地球北纬70°以北的地区,一年连续约2个月的时间没有夜晚,该地区没有夜晚的时间约占全年的百分之十六点七,横线上的数写作( )。
9.如果(A,B,C均不为0),那么A,B,C这三个数中,最大的数是 ,最小的数是 。
10.( )的倒数是4;0.3与( )互为倒数。
11.一瓶食用油250ml,用了20%后,还剩( )ml。
12.如果全班某次数学测试的平均成绩为83分,某同学得了85分,记作﹢2,那么得90分和80分,应分别记作( )和( )。
13.一件衬衫降价10%后,售价是135元,这件衬衫原来的售价是( )元。
14.、、分别同乘一个分数,积都是整数.这个分数最小是 .
三、判断题
15.一袋苹果重10%kg。( )
16.体育馆在学校北偏东30°方向400米处,这是以体育馆为观测点。( )
17.如果a是一个大于0且小于1的数,那么a2<2a。( )
18.六(1)班学生64人,今天全部到校,出勤率为64%.( )
19.表示某种食品营养成分的含量,用扇形统计图比较合适。( )
20.比、分数、除法之间既有联系又有区别. ( )
21.3千克的和9千克的一样重。( )
22.投掷一枚硬币3次,至少有两次出现同一面。( )
四、计算题
23.口算。
3.6÷1.2=
24.下面各题,怎样简便就怎样算。
25.求图中阴影部分的面积(单位:cm)。
26.求出下面各图形的体积.(单位:cm)
五、作图题
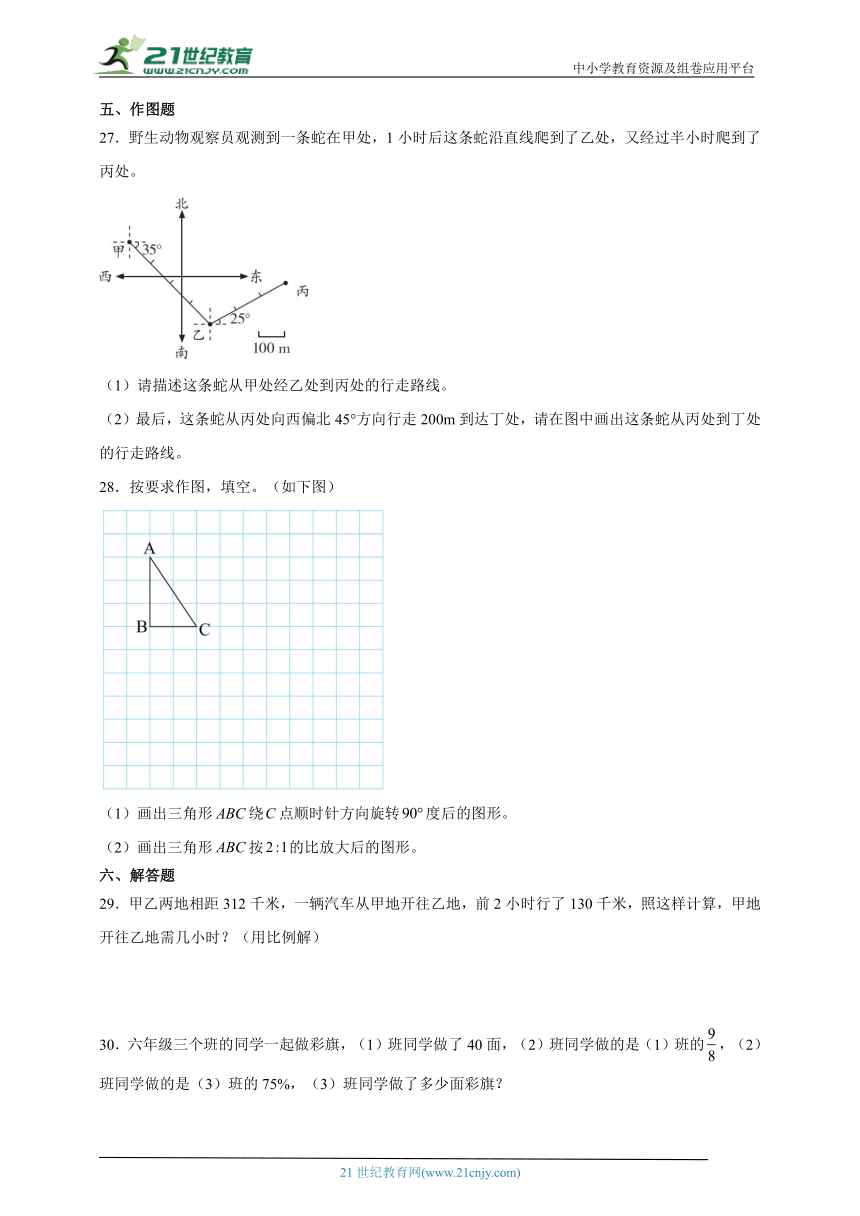
27.野生动物观察员观测到一条蛇在甲处,1小时后这条蛇沿直线爬到了乙处,又经过半小时爬到了丙处。
(1)请描述这条蛇从甲处经乙处到丙处的行走路线。
(2)最后,这条蛇从丙处向西偏北45°方向行走200m到达丁处,请在图中画出这条蛇从丙处到丁处的行走路线。
28.按要求作图,填空。(如下图)
(1)画出三角形绕点顺时针方向旋转度后的图形。
(2)画出三角形按的比放大后的图形。
六、解答题
29.甲乙两地相距312千米,一辆汽车从甲地开往乙地,前2小时行了130千米,照这样计算,甲地开往乙地需几小时?(用比例解)
30.六年级三个班的同学一起做彩旗,(1)班同学做了40面,(2)班同学做的是(1)班的,(2)班同学做的是(3)班的75%,(3)班同学做了多少面彩旗?
31.把一个长8分米、宽6.28分米、高4分米的长方体橡皮泥捏成一个底面半径是4分米的圆柱体,这个圆柱的高是多少分米?
32.一个圆锥形沙堆,底面积是25.12平方米,高是2.4米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
33.大广高速有一段公路需要维修,甲工程队单独完成要20天,乙工程队单独完成要16天,如果甲队先做了5天,剩下的由乙队完成,还需要多少天完成这项工程?
34.做一个底面直径8分米、高0.6米的圆柱形的铁皮油桶(有盖),
(1)做这个油桶至少需要多少平方分米的铁皮?(得数保留整数)
(2)如果每升油重0.65千克,这个油桶最多可以装多少千克?(得数保留整数)
35.如图是从一段钢材上截下的一段(单位:厘米),如果每立方厘米的钢材重7.8克,这段钢材重多少克?
36.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
答案与解析
1.D
【精讲精析】百分数表示一个数是另一个数的百分之几,又叫百分率或百分比;它只能表示两个数之间的倍比关系,不表示具体的数量,所以后面不带单位名称。
【解题思路】A.吨是具体的数量,不能用百分数表示;
B.千克是具体的数量,不能用百分数表示;
C.米是具体的数量,不能用百分数表示;
D.表示用去的是这根绳子的,即用去了75%,能用百分数表示;
故答案为:D
【要点提示】本题考查百分数与分数的区分,明确百分数不能表示具体的数量。
2.C
【精讲精析】根据题意,把5克盐溶在50克水中,那么盐水质量为:(50+5)克,盐与盐水的质量比:5∶(50+5),再根据比的基本性质进行化简即可;据此解答。
【解题思路】5∶(50+5)
=5∶55
=1∶11
=
所以,盐与盐水的质量比是;
故答案为:C
【要点提示】此题考查了比以及比的化简,关键熟记化简方法。
3.C
【解题思路】连接圆周上两点并通过圆心的线段,是圆的直径。一个圆有无数条直径。
故答案为:C
4.B
【精讲精析】要求这幅图的比例尺,首先要从条件中找这种精密零件的图上距离和实际距离,然后根据比例尺的计算公式算出答案。
【解题思路】8分米∶8毫米,
=800毫米∶8毫米,
=100∶1;
答:这幅图的比例尺是100∶1。
故答案为:B
【要点提示】像这种求比例尺的题目单位一般不相同,因此首先要统一单位再计算。
5.B
【精讲精析】向北和向南是具有相反意义的两种量,向北用“﹣”表示,那么向南用“﹢”表示,据此解答。
【解题思路】乐乐向北走40米,记作﹣40米,那么他向南走100米,记作﹢100米。
故答案为:B
【要点提示】掌握正负数的意义和表示方法是解答题目的关键。
6.B
【精讲精析】利用赋值法,令a=40,分别求出各算式的值,再比较即可。
【解题思路】令a=40。
A.40×=25
B.40÷=40×=64
C.40÷=40×=30
D.
64>30>25>
故答案为:B
7.C
【精讲精析】甲、乙二人的速度是不变的,则速度比也是不变的,据“甲跑到第4层时,乙恰好到第3层”可知,甲乙的速度之比为(4-1)∶(3-1)=3∶2,甲跑到第16层时,跑了(16-1)=15层,再据乙的速度=×甲的速度,即可求出乙跑的层数,再加1,就是乙所在的楼层。
【解题思路】甲乙的速度之比:(4-1)∶(3-1)=3∶2
乙跑的层数:(16-1)×
=15×
=10(层)
乙所在的楼层:10+1=11(层)
故答案为:C。
【要点提示】明确甲乙二人的速度比是解决本题的关键。
8.16.7%
【解题思路】略。
9. B A
【精讲精析】假设,分别计算出A、B、C,再进行比较即可。
【解题思路】假设,
则A,B,C;
因为,所以B>C>A。
【要点提示】本题采用了假设法,题目具体化,进而求出A、B、C,再进行比较。
10.
【精讲精析】根据倒数的含义:乘积为1的两个数互为倒数。所以求一个数的倒数,可以用1除以这个数,即1除以4可得解;把小数0.3化成分数,再将分子、分母调换位置,即可得解。
【解题思路】1÷4=
即的倒数是4;
0.3=,与互为倒数,所以0.3与互为倒数。
【要点提示】此题主要考查倒数的认识,关键是掌握求一个数的倒数的方法。
11.200
【精讲精析】把一瓶食用油的总量看作单位“1”,根据求一个数的百分之几是多少,用乘法计算,列式:250×(1-20%),求出剩下的油量。
【解题思路】250×(1-20%)
=250×0.8
=200(ml)
所以,一瓶食用油250ml,用了20%后,还剩200ml。
12. ﹢7 ﹣3
【精讲精析】
此题主要用正负数来表示具有意义相反的两种量:选83分为标准记为0,超过部分为正,不足的部分为负,直接得出结论即可。
【解题思路】
90-83=7(分)
83-80=3(分)
平均成绩为83分,某同学考了85分,记作﹢2,
得分90分和80分应分别记作﹢7和﹣3。
13.150
【精讲精析】把这件衬衫的原价看作单位“1”,现价占原价的(1-10%),根据“量÷对应的百分率”求出这件衬衫的原价,据此解答。
【解题思路】135÷(1-10%)
=135÷0.9
=150(元)
所以,这件衬衫原来的售价是150元。
【要点提示】已知比一个数少百分之几的数是多少,求这个数用除法计算。
14.
【解题思路】试题分析:根据题意得出要求的最小分数的分母应该为5、15、和20的最大公因数数,分子为3、7、9的最小公倍数,由此解答即可.
解:5、15和20的最大公因数为5;
3.7.9的最小公倍数为:7×9=63,
所以要求的分数为.
故答案为.
点评:本题主要是灵活应用求最小公倍数与最大公因数的方法解决问题.
15.×
【精讲精析】百分数是一种特殊的分数,表示两个数之间的倍比关系,不表示具体的数量,所以后面不带单位名称,据此可以判断。
【解题思路】10%是百分数,不表示具体的数量,后面不能带单位,所以原题说法错误。
故答案为:×
16.×
【精讲精析】以平面图上的“上北下南,左西右东”为准,体育馆在学校北偏东30°方向上是以学校的位置为观测点,据此判断。
【解题思路】体育馆在学校北偏东30°方向400米处,这是以学校为观测点。
原题说法错误。
故答案为:×
【要点提示】本题考查根据方向、角度与距离判定物体位置的方法。
17.√
【精讲精析】根据题意,假设a为,分别计算出a2和2a,再进行比较即可。
【解题思路】假设a为;
a2 =×=;
2a=2×=;
<;
故答案为:√。
【要点提示】本题采用了假设法,使题目变具体化、简单化;注意区分a2表示两个a相乘,2a表示两个a相加。
18.×
19.√
【精讲精析】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系;条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;根据不同统计图的特征进行判断即可。
【解题思路】由分析可知:表示某种食品营养成分的含量,用扇形统计图比较合适,说法正确。
故答案为:√
【要点提示】明确数据的特征选取合适的统计图是解答本题的关键。
20.√
【解题思路】根据比、分数、除法之间的关系,比的前项相当于分子、被除数,比号相当于分数线、除号,后项相当于分母、除数;比值相当于分数值,商;它们之间有联系;
比表示两个数之间的关系,分数是一个数值,除法是一种运算,它们之间又有区别.
故答案为√.
21.√
【精讲精析】先利用乘法分别求出3千克的和9千克的是多少千克,再判断二者是否一样重即可。
【解题思路】3×=(千克)
9×=(千克)
所以3千克的和9千克的一样重。
所以判断正确。
【要点提示】本题考查了分数乘法,求一个数的几分之几是多少,用乘法。
22.√
【精讲精析】假设把投掷硬币的次数——3次平均分配给硬币的正反两面,每个面出现1次,剩下的1次不管哪个面朝上,总有一面至少出现了2次。
【解题思路】把3次看作苹果数,硬币的两面看作2个抽屉,因为3÷2=1(次)……1(次),1+1=2(次),所以投掷3次硬币时,至少有两次出现同一面。
故答案安为√。
【要点提示】投掷一枚硬币3次,至少有两次出现同一面。这正符合把n+1个苹果放到n个抽屉中,总有一个抽屉至少有2个苹果的原理。
23.;;;3;
;1;;
24.;46;
;
【精讲精析】(1)先把除法转化为乘法,再逆用乘法分配律简算。
(2)利用乘法分配律简算。
(3)先算分数除法转化为分数乘法,即==,再利用加法结合律先算。
(4)先分别把0.25和25%化成分数,再逆用乘法分配律简算。
【解题思路】
=
=
=
=
=
=12+16+18
=46
=
=
=
=+1
=1
=
=
=1×
=
25.54cm2
【精讲精析】观察图形可知,下面阴影部分的面积=梯形的面积-半圆的面积,上面阴影部分的面积=半圆的面积-三角形的面积;
那么整个图形的阴影部分的面积=梯形的面积-半圆的面积+半圆的面积-三角形的面积=梯形的面积-三角形的面积;
根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,代入数据计算求解。
【解题思路】圆的直径:6×2=12(cm)
梯形的面积:
(12+18)×6÷2
=30×6÷2
=90(cm2)
三角形的面积:
12×6÷2
=72÷2
=36(cm2)
阴影部分的面积:
90-36=54(cm2)
图中阴影部分的面积54cm2。
26.75.36立方厘米
【解题思路】试题分析:根据圆柱的体积公式:v=sh,把数据分别代入公式解答.
解: 3.14×22×6
=3.14×4×6
=75.36(立方厘米)
答:这个圆柱的体积是75.36立方厘米.
27.见详解
【精讲精析】(1)以甲为观测点,乙在甲的东偏南35°(或南偏东55°)方向100×4=400米处;以乙为观测点,丙在乙的东偏北25°(或北偏东65°)方向3×100=300米处;
(2)以丙为观测点,在丙的西偏北45°方向截取200÷100=2个单位长度,终点处标注丁即可。
【解题思路】(1)蛇从甲处出发向东偏南35°(或南偏东55°)方向飞行400米到达乙处,再从乙处出发向东偏北25°(或北偏东65°)方向飞行300米到达丙处。
(2)如图:
28.
【精讲精析】旋转图形,将与旋转中心连接的线段绕顺时针方向旋转90°,再将各点顺次连接。
图形的放大,将各边的长度按照放大的比例算出,再依次画出连接即可。
【解题思路】将BC和AC边绕C点顺时针旋转90°,连接即可。
BC和AC边原来长度是2个格子和3个格子,放大之后长度分别为4个格子和6个格子,画出连接即可。
【要点提示】此题考查图形的旋转以及图形的放大,旋转一定要注意好旋转中心,旋转方向和角度。
29.4.8小时
【精讲精析】根据路程÷时间=速度可知:这辆汽车的速度是一定的,即行驶的路程与时间的比值是一定的,符合正比例的意义,则行驶的路程与时间成正比例,据此即可列比例求解。
【解题思路】解:设甲地开往乙地需x小时,
130∶2=312∶x
130×x=2×312
130x=624
x=624÷130
x=4.8
答:甲地开往乙地需4.8小时。
【要点提示】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
30.60面
【精讲精析】把(1)班同学做彩旗的数量看作单位“1”,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用(1)班同学做彩旗的数量乘即可求出(2)班同学做彩旗的数量;
再把(3)班同学做彩旗的数量看作单位“1”,单位“1”未知,根据百分数除法的意义,已知一个数的百分之几是多少,求这个数,用除法,用(2)班同学做彩旗的数量除以75%,即可求出(3)班同学做了多少面彩旗。
【解题思路】
=
=60(面)
答:(3)班同学做了60面彩旗。
【要点提示】此题的解题关键是理解分数乘法和百分数除法的意义,掌握求一个数的几分之几是多少和已知一个数的百分之几是多少,求这个数的计算方法,从而解决问题。
31.4分米
【精讲精析】首先根据长方体的体积公式:V=abh,求出长方体橡皮泥的体积,再根据圆柱的体积公式:V=Sh,已知圆柱的体积与长方体的体积相等,所以用圆柱的体积除以底面积即可求出圆柱的高,据此解答。
【解题思路】8×6.28×4÷(3.14×42)
=50.24×4÷(3.14×16)
=200.96÷50.24
=4(分米)
答:这个圆柱的高是4分米。
【要点提示】本题主要考查长方体的体积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
32.100.48米
【精讲精析】根据圆锥体积=底面积×高÷3,求出沙堆体积,用沙堆体积÷公路截面=能铺的长度。
【解题思路】2厘米=0.02米
25.12×2.4÷3÷(10×0.02)
=20.096÷0.2
=100.48(米)
答:能铺100.48米。
【要点提示】本题考查了圆锥和长方体体积,长方体体积=长×宽×高=底面积×高=截面×长。
33.12天
【精讲精析】将这项工程看作单位“1”,那么甲队每天完成,乙队每天完成。工作效率×工作时间=工作总量,据此求出甲队做了几分之几,从而利用减法求出还剩下几分之几没有做。工作总量÷工作效率=工作时间,将剩下没做的除以乙队的工作效率,即可求出还需要几天完成这项工程。
【解题思路】(1-×5)÷
=(1-)÷
=÷
=×16
=12(天)
答:还需要12天完成这项工程。
【要点提示】本题考查了工程问题,掌握工作时间、工作总量和工作效率的关系是解题的关键。
34.(1)251.2平方分米;(2)196千克
【精讲精析】(1)0.6米=6分米,根据圆柱的表面积公式:S=2πr2+πdh,用2×3.14×(8÷2)2+3.14×8×6即可求出油桶的表面积;
(2)根据圆柱的体积公式:V=πr2h,用3.14×(8÷2)2×6即可求出油桶的体积,再把单位换成升,最后乘0.65即可求出油的千克数。
【解题思路】(1)0.6米=6分米
2×3.14×(8÷2)2+3.14×8×6
=2×3.14×42+3.14×8×6
=2×3.14×16+3.14×8×6
=100.48+150.72
=251.2(平方分米)
答:做这个油桶至少需要251.2平方分米的铁皮。
(2)3.14×(8÷2)2×6
=3.14×42×6
=3.14×16×6
=301.44(立方分米)
301.44立方分米=301.44升
301.44×0.65≈196(千克)
答:这个油桶最多可以装196千克。
【要点提示】本题主要考查了圆柱的表面积公式、体积公式的灵活应用。
35.881.712克
【解题思路】如果这个图再增加一半,可以拼成一个底面直径是4厘米,高(10+8)厘米的圆柱体,根据圆柱体的体积公式,求出这个圆柱体的体积,再除以2求出图形的体积,然后再乘7.8克,即可求出这段钢材重多少克。
【解答】3.14×(4÷2)2×(10+8)
=3.14×4×18
=12.56×18
=226.08(立方厘米)
226.08÷2×7.8
=113.04×7.8
=881.712(克)
答:这段钢材重881.712克。
36.12套
【精讲精析】把这笔捐款的数目看作单位“1”,先求出桌子和椅子的单价,相加后得到配成一套后的单价,最后依据数量=总价÷单价即可解答。
【解题思路】
1÷(+)
=
=
=
=12(套)
答:这些钱可以买12套办公桌椅。
【要点提示】本题考查了分数除法的应用。求得配成一套后的单价,依据数量=总价÷单价进行计算是解答的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年重点中学小升初择校分班考前冲刺预测卷人教版
一、选择题
1.下面各数能用百分数表示的是( )。
A.一辆货车载重约吨 B.大米比面粉多千克
C.一根绳子长米 D.一根绳子,用去了
2.把5克盐溶在50克水中,盐与盐水的质量比是( )。
A. B. C. D.
3.一个圆有( )直径。
A.1条 B.2条 C.无数条 D.0条
4.一种微型零件,零件实际长度是8毫米,而画到纸上是8分米,这幅图的比例尺是( )
A.1∶100 B.100∶1 C.1∶1000 D.1000∶1
5.乐乐向北走40米,记作﹣40米,那么他向南走100米,记作( )。
A.﹣100米 B.﹢100米 C.﹣140米 D.140米
6.若a是非零的自然数,下列算式中的计算结果最大的是( )。
A.a× B.a÷ C.a÷ D.÷a
7.甲、乙二人从底楼(第一层)开始比赛爬楼梯(每两层之间楼梯的级数相同)甲跑到第4层时,乙恰好到第3层,照这样的速度,甲跑到第16层时,乙跑到( )层。
A.9 B.10 C.11 D.12
二、填空题
8.在地球北纬70°以北的地区,一年连续约2个月的时间没有夜晚,该地区没有夜晚的时间约占全年的百分之十六点七,横线上的数写作( )。
9.如果(A,B,C均不为0),那么A,B,C这三个数中,最大的数是 ,最小的数是 。
10.( )的倒数是4;0.3与( )互为倒数。
11.一瓶食用油250ml,用了20%后,还剩( )ml。
12.如果全班某次数学测试的平均成绩为83分,某同学得了85分,记作﹢2,那么得90分和80分,应分别记作( )和( )。
13.一件衬衫降价10%后,售价是135元,这件衬衫原来的售价是( )元。
14.、、分别同乘一个分数,积都是整数.这个分数最小是 .
三、判断题
15.一袋苹果重10%kg。( )
16.体育馆在学校北偏东30°方向400米处,这是以体育馆为观测点。( )
17.如果a是一个大于0且小于1的数,那么a2<2a。( )
18.六(1)班学生64人,今天全部到校,出勤率为64%.( )
19.表示某种食品营养成分的含量,用扇形统计图比较合适。( )
20.比、分数、除法之间既有联系又有区别. ( )
21.3千克的和9千克的一样重。( )
22.投掷一枚硬币3次,至少有两次出现同一面。( )
四、计算题
23.口算。
3.6÷1.2=
24.下面各题,怎样简便就怎样算。
25.求图中阴影部分的面积(单位:cm)。
26.求出下面各图形的体积.(单位:cm)
五、作图题
27.野生动物观察员观测到一条蛇在甲处,1小时后这条蛇沿直线爬到了乙处,又经过半小时爬到了丙处。
(1)请描述这条蛇从甲处经乙处到丙处的行走路线。
(2)最后,这条蛇从丙处向西偏北45°方向行走200m到达丁处,请在图中画出这条蛇从丙处到丁处的行走路线。
28.按要求作图,填空。(如下图)
(1)画出三角形绕点顺时针方向旋转度后的图形。
(2)画出三角形按的比放大后的图形。
六、解答题
29.甲乙两地相距312千米,一辆汽车从甲地开往乙地,前2小时行了130千米,照这样计算,甲地开往乙地需几小时?(用比例解)
30.六年级三个班的同学一起做彩旗,(1)班同学做了40面,(2)班同学做的是(1)班的,(2)班同学做的是(3)班的75%,(3)班同学做了多少面彩旗?
31.把一个长8分米、宽6.28分米、高4分米的长方体橡皮泥捏成一个底面半径是4分米的圆柱体,这个圆柱的高是多少分米?
32.一个圆锥形沙堆,底面积是25.12平方米,高是2.4米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
33.大广高速有一段公路需要维修,甲工程队单独完成要20天,乙工程队单独完成要16天,如果甲队先做了5天,剩下的由乙队完成,还需要多少天完成这项工程?
34.做一个底面直径8分米、高0.6米的圆柱形的铁皮油桶(有盖),
(1)做这个油桶至少需要多少平方分米的铁皮?(得数保留整数)
(2)如果每升油重0.65千克,这个油桶最多可以装多少千克?(得数保留整数)
35.如图是从一段钢材上截下的一段(单位:厘米),如果每立方厘米的钢材重7.8克,这段钢材重多少克?
36.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
答案与解析
1.D
【精讲精析】百分数表示一个数是另一个数的百分之几,又叫百分率或百分比;它只能表示两个数之间的倍比关系,不表示具体的数量,所以后面不带单位名称。
【解题思路】A.吨是具体的数量,不能用百分数表示;
B.千克是具体的数量,不能用百分数表示;
C.米是具体的数量,不能用百分数表示;
D.表示用去的是这根绳子的,即用去了75%,能用百分数表示;
故答案为:D
【要点提示】本题考查百分数与分数的区分,明确百分数不能表示具体的数量。
2.C
【精讲精析】根据题意,把5克盐溶在50克水中,那么盐水质量为:(50+5)克,盐与盐水的质量比:5∶(50+5),再根据比的基本性质进行化简即可;据此解答。
【解题思路】5∶(50+5)
=5∶55
=1∶11
=
所以,盐与盐水的质量比是;
故答案为:C
【要点提示】此题考查了比以及比的化简,关键熟记化简方法。
3.C
【解题思路】连接圆周上两点并通过圆心的线段,是圆的直径。一个圆有无数条直径。
故答案为:C
4.B
【精讲精析】要求这幅图的比例尺,首先要从条件中找这种精密零件的图上距离和实际距离,然后根据比例尺的计算公式算出答案。
【解题思路】8分米∶8毫米,
=800毫米∶8毫米,
=100∶1;
答:这幅图的比例尺是100∶1。
故答案为:B
【要点提示】像这种求比例尺的题目单位一般不相同,因此首先要统一单位再计算。
5.B
【精讲精析】向北和向南是具有相反意义的两种量,向北用“﹣”表示,那么向南用“﹢”表示,据此解答。
【解题思路】乐乐向北走40米,记作﹣40米,那么他向南走100米,记作﹢100米。
故答案为:B
【要点提示】掌握正负数的意义和表示方法是解答题目的关键。
6.B
【精讲精析】利用赋值法,令a=40,分别求出各算式的值,再比较即可。
【解题思路】令a=40。
A.40×=25
B.40÷=40×=64
C.40÷=40×=30
D.
64>30>25>
故答案为:B
7.C
【精讲精析】甲、乙二人的速度是不变的,则速度比也是不变的,据“甲跑到第4层时,乙恰好到第3层”可知,甲乙的速度之比为(4-1)∶(3-1)=3∶2,甲跑到第16层时,跑了(16-1)=15层,再据乙的速度=×甲的速度,即可求出乙跑的层数,再加1,就是乙所在的楼层。
【解题思路】甲乙的速度之比:(4-1)∶(3-1)=3∶2
乙跑的层数:(16-1)×
=15×
=10(层)
乙所在的楼层:10+1=11(层)
故答案为:C。
【要点提示】明确甲乙二人的速度比是解决本题的关键。
8.16.7%
【解题思路】略。
9. B A
【精讲精析】假设,分别计算出A、B、C,再进行比较即可。
【解题思路】假设,
则A,B,C;
因为,所以B>C>A。
【要点提示】本题采用了假设法,题目具体化,进而求出A、B、C,再进行比较。
10.
【精讲精析】根据倒数的含义:乘积为1的两个数互为倒数。所以求一个数的倒数,可以用1除以这个数,即1除以4可得解;把小数0.3化成分数,再将分子、分母调换位置,即可得解。
【解题思路】1÷4=
即的倒数是4;
0.3=,与互为倒数,所以0.3与互为倒数。
【要点提示】此题主要考查倒数的认识,关键是掌握求一个数的倒数的方法。
11.200
【精讲精析】把一瓶食用油的总量看作单位“1”,根据求一个数的百分之几是多少,用乘法计算,列式:250×(1-20%),求出剩下的油量。
【解题思路】250×(1-20%)
=250×0.8
=200(ml)
所以,一瓶食用油250ml,用了20%后,还剩200ml。
12. ﹢7 ﹣3
【精讲精析】
此题主要用正负数来表示具有意义相反的两种量:选83分为标准记为0,超过部分为正,不足的部分为负,直接得出结论即可。
【解题思路】
90-83=7(分)
83-80=3(分)
平均成绩为83分,某同学考了85分,记作﹢2,
得分90分和80分应分别记作﹢7和﹣3。
13.150
【精讲精析】把这件衬衫的原价看作单位“1”,现价占原价的(1-10%),根据“量÷对应的百分率”求出这件衬衫的原价,据此解答。
【解题思路】135÷(1-10%)
=135÷0.9
=150(元)
所以,这件衬衫原来的售价是150元。
【要点提示】已知比一个数少百分之几的数是多少,求这个数用除法计算。
14.
【解题思路】试题分析:根据题意得出要求的最小分数的分母应该为5、15、和20的最大公因数数,分子为3、7、9的最小公倍数,由此解答即可.
解:5、15和20的最大公因数为5;
3.7.9的最小公倍数为:7×9=63,
所以要求的分数为.
故答案为.
点评:本题主要是灵活应用求最小公倍数与最大公因数的方法解决问题.
15.×
【精讲精析】百分数是一种特殊的分数,表示两个数之间的倍比关系,不表示具体的数量,所以后面不带单位名称,据此可以判断。
【解题思路】10%是百分数,不表示具体的数量,后面不能带单位,所以原题说法错误。
故答案为:×
16.×
【精讲精析】以平面图上的“上北下南,左西右东”为准,体育馆在学校北偏东30°方向上是以学校的位置为观测点,据此判断。
【解题思路】体育馆在学校北偏东30°方向400米处,这是以学校为观测点。
原题说法错误。
故答案为:×
【要点提示】本题考查根据方向、角度与距离判定物体位置的方法。
17.√
【精讲精析】根据题意,假设a为,分别计算出a2和2a,再进行比较即可。
【解题思路】假设a为;
a2 =×=;
2a=2×=;
<;
故答案为:√。
【要点提示】本题采用了假设法,使题目变具体化、简单化;注意区分a2表示两个a相乘,2a表示两个a相加。
18.×
19.√
【精讲精析】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系;条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;根据不同统计图的特征进行判断即可。
【解题思路】由分析可知:表示某种食品营养成分的含量,用扇形统计图比较合适,说法正确。
故答案为:√
【要点提示】明确数据的特征选取合适的统计图是解答本题的关键。
20.√
【解题思路】根据比、分数、除法之间的关系,比的前项相当于分子、被除数,比号相当于分数线、除号,后项相当于分母、除数;比值相当于分数值,商;它们之间有联系;
比表示两个数之间的关系,分数是一个数值,除法是一种运算,它们之间又有区别.
故答案为√.
21.√
【精讲精析】先利用乘法分别求出3千克的和9千克的是多少千克,再判断二者是否一样重即可。
【解题思路】3×=(千克)
9×=(千克)
所以3千克的和9千克的一样重。
所以判断正确。
【要点提示】本题考查了分数乘法,求一个数的几分之几是多少,用乘法。
22.√
【精讲精析】假设把投掷硬币的次数——3次平均分配给硬币的正反两面,每个面出现1次,剩下的1次不管哪个面朝上,总有一面至少出现了2次。
【解题思路】把3次看作苹果数,硬币的两面看作2个抽屉,因为3÷2=1(次)……1(次),1+1=2(次),所以投掷3次硬币时,至少有两次出现同一面。
故答案安为√。
【要点提示】投掷一枚硬币3次,至少有两次出现同一面。这正符合把n+1个苹果放到n个抽屉中,总有一个抽屉至少有2个苹果的原理。
23.;;;3;
;1;;
24.;46;
;
【精讲精析】(1)先把除法转化为乘法,再逆用乘法分配律简算。
(2)利用乘法分配律简算。
(3)先算分数除法转化为分数乘法,即==,再利用加法结合律先算。
(4)先分别把0.25和25%化成分数,再逆用乘法分配律简算。
【解题思路】
=
=
=
=
=
=12+16+18
=46
=
=
=
=+1
=1
=
=
=1×
=
25.54cm2
【精讲精析】观察图形可知,下面阴影部分的面积=梯形的面积-半圆的面积,上面阴影部分的面积=半圆的面积-三角形的面积;
那么整个图形的阴影部分的面积=梯形的面积-半圆的面积+半圆的面积-三角形的面积=梯形的面积-三角形的面积;
根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,代入数据计算求解。
【解题思路】圆的直径:6×2=12(cm)
梯形的面积:
(12+18)×6÷2
=30×6÷2
=90(cm2)
三角形的面积:
12×6÷2
=72÷2
=36(cm2)
阴影部分的面积:
90-36=54(cm2)
图中阴影部分的面积54cm2。
26.75.36立方厘米
【解题思路】试题分析:根据圆柱的体积公式:v=sh,把数据分别代入公式解答.
解: 3.14×22×6
=3.14×4×6
=75.36(立方厘米)
答:这个圆柱的体积是75.36立方厘米.
27.见详解
【精讲精析】(1)以甲为观测点,乙在甲的东偏南35°(或南偏东55°)方向100×4=400米处;以乙为观测点,丙在乙的东偏北25°(或北偏东65°)方向3×100=300米处;
(2)以丙为观测点,在丙的西偏北45°方向截取200÷100=2个单位长度,终点处标注丁即可。
【解题思路】(1)蛇从甲处出发向东偏南35°(或南偏东55°)方向飞行400米到达乙处,再从乙处出发向东偏北25°(或北偏东65°)方向飞行300米到达丙处。
(2)如图:
28.
【精讲精析】旋转图形,将与旋转中心连接的线段绕顺时针方向旋转90°,再将各点顺次连接。
图形的放大,将各边的长度按照放大的比例算出,再依次画出连接即可。
【解题思路】将BC和AC边绕C点顺时针旋转90°,连接即可。
BC和AC边原来长度是2个格子和3个格子,放大之后长度分别为4个格子和6个格子,画出连接即可。
【要点提示】此题考查图形的旋转以及图形的放大,旋转一定要注意好旋转中心,旋转方向和角度。
29.4.8小时
【精讲精析】根据路程÷时间=速度可知:这辆汽车的速度是一定的,即行驶的路程与时间的比值是一定的,符合正比例的意义,则行驶的路程与时间成正比例,据此即可列比例求解。
【解题思路】解:设甲地开往乙地需x小时,
130∶2=312∶x
130×x=2×312
130x=624
x=624÷130
x=4.8
答:甲地开往乙地需4.8小时。
【要点提示】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
30.60面
【精讲精析】把(1)班同学做彩旗的数量看作单位“1”,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用(1)班同学做彩旗的数量乘即可求出(2)班同学做彩旗的数量;
再把(3)班同学做彩旗的数量看作单位“1”,单位“1”未知,根据百分数除法的意义,已知一个数的百分之几是多少,求这个数,用除法,用(2)班同学做彩旗的数量除以75%,即可求出(3)班同学做了多少面彩旗。
【解题思路】
=
=60(面)
答:(3)班同学做了60面彩旗。
【要点提示】此题的解题关键是理解分数乘法和百分数除法的意义,掌握求一个数的几分之几是多少和已知一个数的百分之几是多少,求这个数的计算方法,从而解决问题。
31.4分米
【精讲精析】首先根据长方体的体积公式:V=abh,求出长方体橡皮泥的体积,再根据圆柱的体积公式:V=Sh,已知圆柱的体积与长方体的体积相等,所以用圆柱的体积除以底面积即可求出圆柱的高,据此解答。
【解题思路】8×6.28×4÷(3.14×42)
=50.24×4÷(3.14×16)
=200.96÷50.24
=4(分米)
答:这个圆柱的高是4分米。
【要点提示】本题主要考查长方体的体积公式、圆柱的体积公式的灵活运用,关键是熟记公式。
32.100.48米
【精讲精析】根据圆锥体积=底面积×高÷3,求出沙堆体积,用沙堆体积÷公路截面=能铺的长度。
【解题思路】2厘米=0.02米
25.12×2.4÷3÷(10×0.02)
=20.096÷0.2
=100.48(米)
答:能铺100.48米。
【要点提示】本题考查了圆锥和长方体体积,长方体体积=长×宽×高=底面积×高=截面×长。
33.12天
【精讲精析】将这项工程看作单位“1”,那么甲队每天完成,乙队每天完成。工作效率×工作时间=工作总量,据此求出甲队做了几分之几,从而利用减法求出还剩下几分之几没有做。工作总量÷工作效率=工作时间,将剩下没做的除以乙队的工作效率,即可求出还需要几天完成这项工程。
【解题思路】(1-×5)÷
=(1-)÷
=÷
=×16
=12(天)
答:还需要12天完成这项工程。
【要点提示】本题考查了工程问题,掌握工作时间、工作总量和工作效率的关系是解题的关键。
34.(1)251.2平方分米;(2)196千克
【精讲精析】(1)0.6米=6分米,根据圆柱的表面积公式:S=2πr2+πdh,用2×3.14×(8÷2)2+3.14×8×6即可求出油桶的表面积;
(2)根据圆柱的体积公式:V=πr2h,用3.14×(8÷2)2×6即可求出油桶的体积,再把单位换成升,最后乘0.65即可求出油的千克数。
【解题思路】(1)0.6米=6分米
2×3.14×(8÷2)2+3.14×8×6
=2×3.14×42+3.14×8×6
=2×3.14×16+3.14×8×6
=100.48+150.72
=251.2(平方分米)
答:做这个油桶至少需要251.2平方分米的铁皮。
(2)3.14×(8÷2)2×6
=3.14×42×6
=3.14×16×6
=301.44(立方分米)
301.44立方分米=301.44升
301.44×0.65≈196(千克)
答:这个油桶最多可以装196千克。
【要点提示】本题主要考查了圆柱的表面积公式、体积公式的灵活应用。
35.881.712克
【解题思路】如果这个图再增加一半,可以拼成一个底面直径是4厘米,高(10+8)厘米的圆柱体,根据圆柱体的体积公式,求出这个圆柱体的体积,再除以2求出图形的体积,然后再乘7.8克,即可求出这段钢材重多少克。
【解答】3.14×(4÷2)2×(10+8)
=3.14×4×18
=12.56×18
=226.08(立方厘米)
226.08÷2×7.8
=113.04×7.8
=881.712(克)
答:这段钢材重881.712克。
36.12套
【精讲精析】把这笔捐款的数目看作单位“1”,先求出桌子和椅子的单价,相加后得到配成一套后的单价,最后依据数量=总价÷单价即可解答。
【解题思路】
1÷(+)
=
=
=
=12(套)
答:这些钱可以买12套办公桌椅。
【要点提示】本题考查了分数除法的应用。求得配成一套后的单价,依据数量=总价÷单价进行计算是解答的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
