1.5《等腰三角形》(含详解)八年级数学上册苏科版
文档属性
| 名称 | 1.5《等腰三角形》(含详解)八年级数学上册苏科版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 06:20:14 | ||
图片预览



文档简介
1.5《等腰三角形》
一、单选题
1.下列命题中,是真命题的是( )
A.等腰三角形两腰上的高相等
B.三角形按边分类可分为等边三角形和不等边三角形
C.等腰三角形的角平分线、中线和高重合
D.有一个角等于的三角形是等边三角形
2.下列条件中不能说明三角形是等腰三角形的是( )
A.有两个内角分别是的三角形
B.有一个角为的直角三角形
C.一个外角是,与它不相邻的一个内角为的三角形
D.有两个内角分别是的三角形
3.如图,李大伯用篱笆搭建了一块四边形土地用来种花,,为四边形土地的一条小路(点E在边上),且恰好平分.若篱笆的长度为5米,篱笆的长度为米,则篱笆的长度是( )
A.米 B.米 C.6米 D.米
4.如图,以正五边形的边为一边,向内作等边三角形,连接,则的度数为( )
A. B. C. D.
5.如图,在中,于点D,E是的中点.若,则的长为( )
A.1 B.2 C.4 D.6
6.如图,等边三角形的边长为9,为边上一动点,为延长线上一动点,交于点,点为中点.若,则长为( )
A.2 B.3 C.4 D.5
7.如图,在 ABC中,,,是高,是中线,AH交BM于点N、于点E,交于点D,连接,则下列结论:①;②;③;④.其中,正确的有( )
A.①②③ B.②③④ C.①②④ D.①②③④
二、填空题
8.如图,在中,点A为外部一点,连接,点A、D、C在一条直线上,,若,则的长为 .
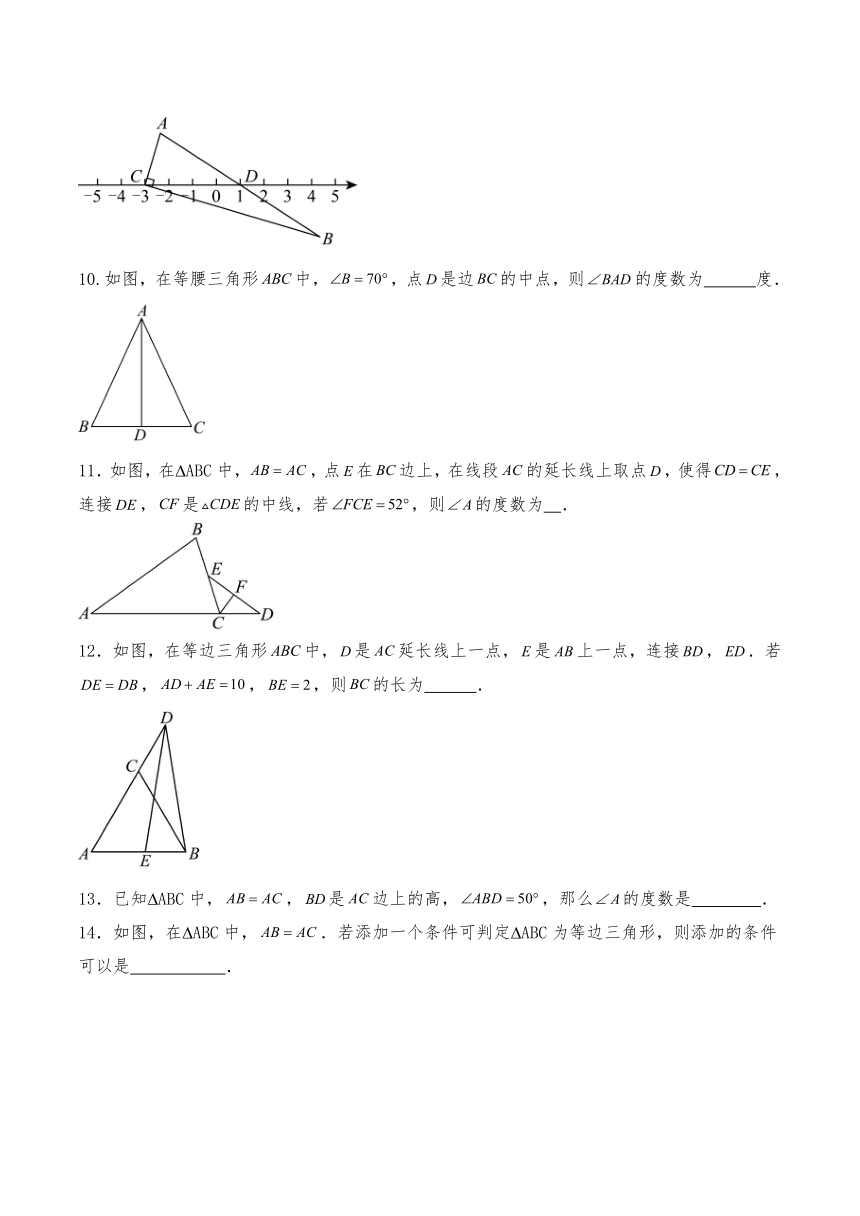
9.如图, ABC的顶点与的中点均在数轴上,且,两点在数轴上对应的数分别为,,当时,的长为 .
10.如图,在等腰三角形中,,点是边的中点,则的度数为 度.
11.如图,在 ABC中,,点在边上,在线段的延长线上取点,使得,连接,是的中线,若,则的度数为 .
12.如图,在等边三角形中,是延长线上一点,是上一点,连接,.若,,,则的长为 .
13.已知 ABC中,,是边上的高,,那么的度数是 .
14.如图,在 ABC中,.若添加一个条件可判定 ABC为等边三角形,则添加的条件可以是 .
三、解答题
15.在学习了等腰三角形的相关知识后,数学学习小组进行了更深入的研究,他们发现一个三角形两边中线相等,则这个三角形是等腰三角形,可利用证明三角形全等得到此结论,请根据他们的想法与思路,完成以下作图和填空:
(1)如图,在 ABC中,点是边上的中点,用尺规过点作边的垂线交于点,连接(不写作法,保留作图痕迹);
(2)已知:在 ABC中,点、点分别是、边上的中点,连接、,过点作于点,过点作于点,满足,求证: ABC是等腰三角形.
证明:点、点分别是、边上的中点,
,,
又,,,
在和中,,,,
在和 CBF中,,,,
,是等腰三角形.
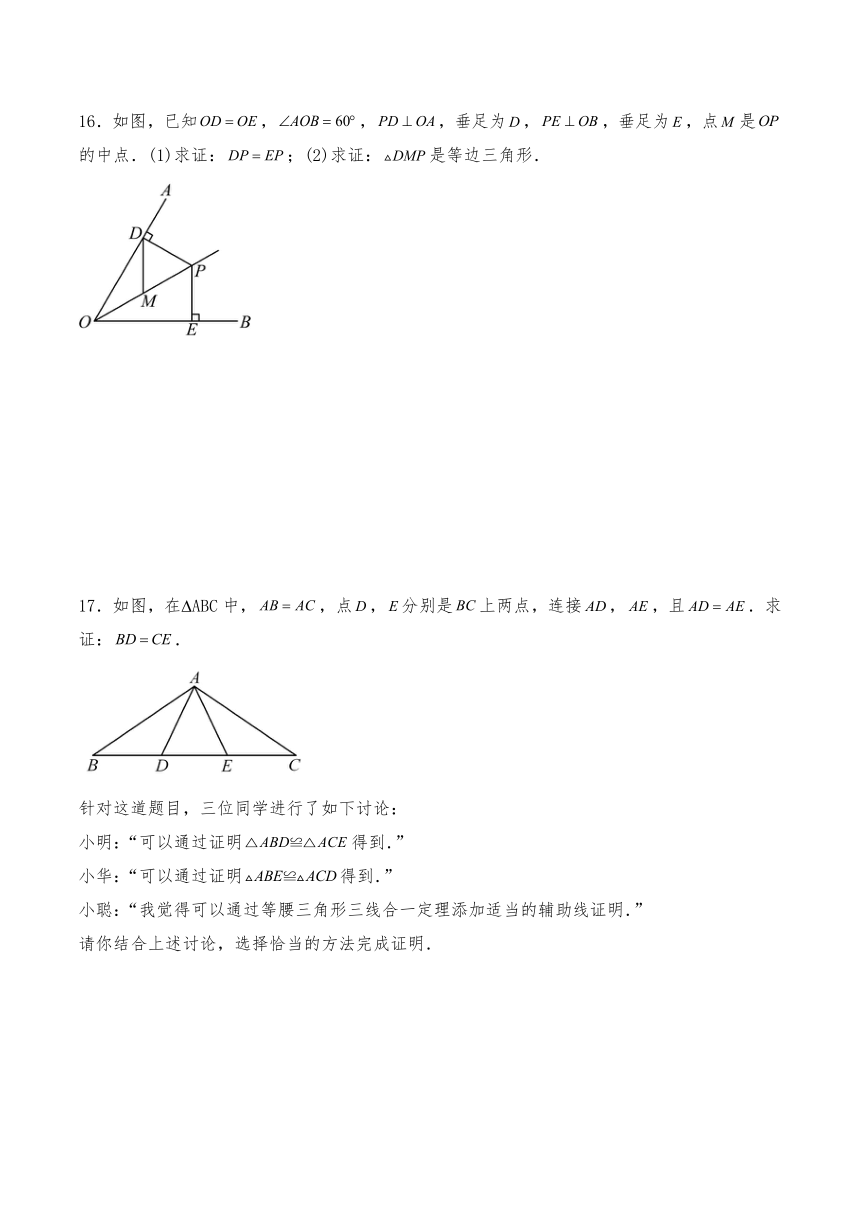
16.如图,已知,,,垂足为,,垂足为,点是的中点.(1)求证:;(2)求证:是等边三角形.
17.如图,在 ABC中,,点,分别是上两点,连接,,且.求证:.
针对这道题目,三位同学进行了如下讨论:
小明:“可以通过证明得到.”
小华:“可以通过证明得到.”
小聪:“我觉得可以通过等腰三角形三线合一定理添加适当的辅助线证明.”
请你结合上述讨论,选择恰当的方法完成证明.
18. 如图, 在 ABC中,于点D,垂直平分,交于点F,交于点E,连接,且.(1)若,求的度数;(2)若 ABC的周长为,,求的长.
19.如图,点O是等边 ABC内一点,D是 ABC外一点,,,,,连接.(1)求证:是等边三角形;(2)当时,试判断的形状,并说明理由;(3)探究:当为多少度时,是等腰三角形.
20.如图,在等边 ABC中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是,与构成的锐角夹角的度数是;并说明理由.
(2)深入探究,将图中的延长至点,使,连接,,如图所示.求证:平分(第一问的结论,本问可直接使用)
21.如图,在中,,点B在边上,且,C是射线上的一个动点(不与点B重合,且),在射线上截取,连接.
(1)当点C在线段上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段与的数量关系为_____;
②如图2,若点C不与点D重合,请证明:;
(2)当点C在线段的延长线上时,直接写出,,之间的数量关系.
参考答案
一、单选题
1.A
【详解】解:A、等腰三角形两腰上的高相等,是真命题,符合题意;
B、三角形按边可分为不等边三角形,等腰三角形,故B是假命题,不符合题意;
C、等腰三角形底边上的高线、顶角的角平分线、底边上的中线重合,故C是假命题,不符合题意;
D、有一个角等于的等腰三角形是等边三角形,故D是假命题,不符合题意.
故选:A.
2.D
【详解】解:A:两内角是,第三角为,存在两个的角,故为等腰三角形,不符合题意;
B:直角三角形中一个角为,则另一锐角为,两角相等,故为等腰直角三角形,不符合题意;
C:外角对应内角为,与它不相邻的内角为,根据三角形外角的性质,另一不相邻内角为,此时三角形内角为,存在两角相等,故为等腰三角形,不符合题意;
D:两内角为,第三角为,三角均不相等,无法构成等腰三角形,符合题意;
故选:D.
3.A
【详解】解:∵,∴,
∵恰好平分,∴,∴,∴,
米,米,米,∴米,故选:A.
4.B
【详解】解:以正五边形的边为一边,向内作等边三角形,,,
是正五边形,,且,
,,,
在等腰中,,则,
,故选:B.
5.B
【详解】解:∵在中,E是的中点, ,∴,
∴,∴,∴是等边三角形,
∵,∴,故选:B
6.B
【详解】解:如下图,过点D作,交于F,
是等边三角形,,,
,是等边三角形,,
点P为中点,,
在和中,,,,,
,,,
设,则,,解得:,,故选:B.
7.D
【详解】解:如图,作交的延长线于.
,,∴ ABC是等腰直角三角形,
∵是高,是中线,∴平分,,,,
,,
,∴,
∵,,
,,,故②③正确,
,,,,
,,,,
,,,
,,,,故①④正确,故选:D.
二、填空题
8.3
【详解】解:∵,∴,∴;
∵,∴,∴,
∴,∴;故答案为:3.
9.8
【详解】解:由题意可得,
,点为的中点,,故答案为:8.
10.
【详解】解:∵在等腰三角形中,点是边的中点,∴,则,
∵,∴故答案为:.
11.
【详解】解:∵,是的中线,∴,
∵,∴,∴,故答案为:.
12.
【详解】解:如图,过作于点,
∵DE=DB,BE=2,,设,则,
∵ ABC是等边三角形,,,,
即,,,故答案为:.
13.或
【分析】本题考查的是三角形的内角和定理的应用,等腰三角形的性质,分情况讨论:当 ABC为锐角三角形时,当 ABC钝角三角形时,结合等腰三角形的性质,即可求解.
【详解】解:如图①,当 ABC为锐角三角形时,;
如图②,当 ABC钝角三角形时,,
所以.
综上,的度数为或.
故答案为:或.
14.(答案不唯一)
【详解】解:①当或时,
∵,∴,即是等边三角形;
②当或或时,
∵,∴是等边三角形;故答案为:(答案不唯一)
三、解答题
15.(1)解:如图所示:
;
(2)证明:点、点分别是、边上的中点,,,
又,,,
在和中,,,,
在和 CBF中,,,,
,是等腰三角形.
故答案为:;;;;.
16.(1)证明:,垂足为D,,垂足为,
在和中,().;
(2)证明:由(1)可知,,
,点是的中点,,
,
又,是等边三角形.
17.小明的方法证明:∵,∴,
∵,∴,∴,∴,∴;
小华的方法证明:∵,∴,
∵,∴,即,∴,∴;
小聪的方法证明:如图,过点作于,
∵,,∴,,∴,即.
18.(1)解:∵,
∴,∴,∴,
∵垂直平分,∴,∴,
∵,∴,∴的度数为;
(2)解:∵,∴,∵,∴,
∵ ABC的周长为,,
∴,解得,,∴的长为.
19.(1)解:∵,∴,又∵,∴是等边三角形;
(2)解:是直角三角形.理由如下:
∵是等边三角形,∴,
∵,,∴,
∴,∴是直角三角形;
(3)解:∵是等边三角形,∴,
∵,,∴,
∵,∴,∴,
∴.
①当时,则,即,∴;
②当时,则,即,∴;
③当时,则,即,∴.
综上所述:当或或时,是等腰三角形.
20.(1)∵ ABC是等边三角形,,
在和中,,,,
,故答案为:,;
(2)证明:由(1)可知,,,
,∴是等边三角形,,
∵ ABC是等边三角形,,,
,即,,
,,
,平分.
21.(1)①解:补全图形如图1所示,
∵,,∴ ABC是等边三角形,∴,∴,
∵,∴,∴,∴,故答案为:;
②证明:如图2,在上截取,连接,
∵,,,∴是等边三角形,,
∴,,∴,
∵,∴,∴,∴,
∵,∴;
(2)解:当点A在点E右边时,如图3,在上截取,连接,
由(1)知,,,
∵,∴;
当点A在点E左边时,如图4,在上截取,连接,
由(1)知,,,∵,∴.
一、单选题
1.下列命题中,是真命题的是( )
A.等腰三角形两腰上的高相等
B.三角形按边分类可分为等边三角形和不等边三角形
C.等腰三角形的角平分线、中线和高重合
D.有一个角等于的三角形是等边三角形
2.下列条件中不能说明三角形是等腰三角形的是( )
A.有两个内角分别是的三角形
B.有一个角为的直角三角形
C.一个外角是,与它不相邻的一个内角为的三角形
D.有两个内角分别是的三角形
3.如图,李大伯用篱笆搭建了一块四边形土地用来种花,,为四边形土地的一条小路(点E在边上),且恰好平分.若篱笆的长度为5米,篱笆的长度为米,则篱笆的长度是( )
A.米 B.米 C.6米 D.米
4.如图,以正五边形的边为一边,向内作等边三角形,连接,则的度数为( )
A. B. C. D.
5.如图,在中,于点D,E是的中点.若,则的长为( )
A.1 B.2 C.4 D.6
6.如图,等边三角形的边长为9,为边上一动点,为延长线上一动点,交于点,点为中点.若,则长为( )
A.2 B.3 C.4 D.5
7.如图,在 ABC中,,,是高,是中线,AH交BM于点N、于点E,交于点D,连接,则下列结论:①;②;③;④.其中,正确的有( )
A.①②③ B.②③④ C.①②④ D.①②③④
二、填空题
8.如图,在中,点A为外部一点,连接,点A、D、C在一条直线上,,若,则的长为 .
9.如图, ABC的顶点与的中点均在数轴上,且,两点在数轴上对应的数分别为,,当时,的长为 .
10.如图,在等腰三角形中,,点是边的中点,则的度数为 度.
11.如图,在 ABC中,,点在边上,在线段的延长线上取点,使得,连接,是的中线,若,则的度数为 .
12.如图,在等边三角形中,是延长线上一点,是上一点,连接,.若,,,则的长为 .
13.已知 ABC中,,是边上的高,,那么的度数是 .
14.如图,在 ABC中,.若添加一个条件可判定 ABC为等边三角形,则添加的条件可以是 .
三、解答题
15.在学习了等腰三角形的相关知识后,数学学习小组进行了更深入的研究,他们发现一个三角形两边中线相等,则这个三角形是等腰三角形,可利用证明三角形全等得到此结论,请根据他们的想法与思路,完成以下作图和填空:
(1)如图,在 ABC中,点是边上的中点,用尺规过点作边的垂线交于点,连接(不写作法,保留作图痕迹);
(2)已知:在 ABC中,点、点分别是、边上的中点,连接、,过点作于点,过点作于点,满足,求证: ABC是等腰三角形.
证明:点、点分别是、边上的中点,
,,
又,,,
在和中,,,,
在和 CBF中,,,,
,是等腰三角形.
16.如图,已知,,,垂足为,,垂足为,点是的中点.(1)求证:;(2)求证:是等边三角形.
17.如图,在 ABC中,,点,分别是上两点,连接,,且.求证:.
针对这道题目,三位同学进行了如下讨论:
小明:“可以通过证明得到.”
小华:“可以通过证明得到.”
小聪:“我觉得可以通过等腰三角形三线合一定理添加适当的辅助线证明.”
请你结合上述讨论,选择恰当的方法完成证明.
18. 如图, 在 ABC中,于点D,垂直平分,交于点F,交于点E,连接,且.(1)若,求的度数;(2)若 ABC的周长为,,求的长.
19.如图,点O是等边 ABC内一点,D是 ABC外一点,,,,,连接.(1)求证:是等边三角形;(2)当时,试判断的形状,并说明理由;(3)探究:当为多少度时,是等腰三角形.
20.如图,在等边 ABC中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是,与构成的锐角夹角的度数是;并说明理由.
(2)深入探究,将图中的延长至点,使,连接,,如图所示.求证:平分(第一问的结论,本问可直接使用)
21.如图,在中,,点B在边上,且,C是射线上的一个动点(不与点B重合,且),在射线上截取,连接.
(1)当点C在线段上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段与的数量关系为_____;
②如图2,若点C不与点D重合,请证明:;
(2)当点C在线段的延长线上时,直接写出,,之间的数量关系.
参考答案
一、单选题
1.A
【详解】解:A、等腰三角形两腰上的高相等,是真命题,符合题意;
B、三角形按边可分为不等边三角形,等腰三角形,故B是假命题,不符合题意;
C、等腰三角形底边上的高线、顶角的角平分线、底边上的中线重合,故C是假命题,不符合题意;
D、有一个角等于的等腰三角形是等边三角形,故D是假命题,不符合题意.
故选:A.
2.D
【详解】解:A:两内角是,第三角为,存在两个的角,故为等腰三角形,不符合题意;
B:直角三角形中一个角为,则另一锐角为,两角相等,故为等腰直角三角形,不符合题意;
C:外角对应内角为,与它不相邻的内角为,根据三角形外角的性质,另一不相邻内角为,此时三角形内角为,存在两角相等,故为等腰三角形,不符合题意;
D:两内角为,第三角为,三角均不相等,无法构成等腰三角形,符合题意;
故选:D.
3.A
【详解】解:∵,∴,
∵恰好平分,∴,∴,∴,
米,米,米,∴米,故选:A.
4.B
【详解】解:以正五边形的边为一边,向内作等边三角形,,,
是正五边形,,且,
,,,
在等腰中,,则,
,故选:B.
5.B
【详解】解:∵在中,E是的中点, ,∴,
∴,∴,∴是等边三角形,
∵,∴,故选:B
6.B
【详解】解:如下图,过点D作,交于F,
是等边三角形,,,
,是等边三角形,,
点P为中点,,
在和中,,,,,
,,,
设,则,,解得:,,故选:B.
7.D
【详解】解:如图,作交的延长线于.
,,∴ ABC是等腰直角三角形,
∵是高,是中线,∴平分,,,,
,,
,∴,
∵,,
,,,故②③正确,
,,,,
,,,,
,,,
,,,,故①④正确,故选:D.
二、填空题
8.3
【详解】解:∵,∴,∴;
∵,∴,∴,
∴,∴;故答案为:3.
9.8
【详解】解:由题意可得,
,点为的中点,,故答案为:8.
10.
【详解】解:∵在等腰三角形中,点是边的中点,∴,则,
∵,∴故答案为:.
11.
【详解】解:∵,是的中线,∴,
∵,∴,∴,故答案为:.
12.
【详解】解:如图,过作于点,
∵DE=DB,BE=2,,设,则,
∵ ABC是等边三角形,,,,
即,,,故答案为:.
13.或
【分析】本题考查的是三角形的内角和定理的应用,等腰三角形的性质,分情况讨论:当 ABC为锐角三角形时,当 ABC钝角三角形时,结合等腰三角形的性质,即可求解.
【详解】解:如图①,当 ABC为锐角三角形时,;
如图②,当 ABC钝角三角形时,,
所以.
综上,的度数为或.
故答案为:或.
14.(答案不唯一)
【详解】解:①当或时,
∵,∴,即是等边三角形;
②当或或时,
∵,∴是等边三角形;故答案为:(答案不唯一)
三、解答题
15.(1)解:如图所示:
;
(2)证明:点、点分别是、边上的中点,,,
又,,,
在和中,,,,
在和 CBF中,,,,
,是等腰三角形.
故答案为:;;;;.
16.(1)证明:,垂足为D,,垂足为,
在和中,().;
(2)证明:由(1)可知,,
,点是的中点,,
,
又,是等边三角形.
17.小明的方法证明:∵,∴,
∵,∴,∴,∴,∴;
小华的方法证明:∵,∴,
∵,∴,即,∴,∴;
小聪的方法证明:如图,过点作于,
∵,,∴,,∴,即.
18.(1)解:∵,
∴,∴,∴,
∵垂直平分,∴,∴,
∵,∴,∴的度数为;
(2)解:∵,∴,∵,∴,
∵ ABC的周长为,,
∴,解得,,∴的长为.
19.(1)解:∵,∴,又∵,∴是等边三角形;
(2)解:是直角三角形.理由如下:
∵是等边三角形,∴,
∵,,∴,
∴,∴是直角三角形;
(3)解:∵是等边三角形,∴,
∵,,∴,
∵,∴,∴,
∴.
①当时,则,即,∴;
②当时,则,即,∴;
③当时,则,即,∴.
综上所述:当或或时,是等腰三角形.
20.(1)∵ ABC是等边三角形,,
在和中,,,,
,故答案为:,;
(2)证明:由(1)可知,,,
,∴是等边三角形,,
∵ ABC是等边三角形,,,
,即,,
,,
,平分.
21.(1)①解:补全图形如图1所示,
∵,,∴ ABC是等边三角形,∴,∴,
∵,∴,∴,∴,故答案为:;
②证明:如图2,在上截取,连接,
∵,,,∴是等边三角形,,
∴,,∴,
∵,∴,∴,∴,
∵,∴;
(2)解:当点A在点E右边时,如图3,在上截取,连接,
由(1)知,,,
∵,∴;
当点A在点E左边时,如图4,在上截取,连接,
由(1)知,,,∵,∴.
同课章节目录
