【暑假温故培优】专题05 三角形-2025年人教版数学四升五暑假温故培优精练(含解析)
文档属性
| 名称 | 【暑假温故培优】专题05 三角形-2025年人教版数学四升五暑假温故培优精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 640.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 18:16:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2025年数学四升五暑假巩固培优精练(人教版)
专题05 是三角形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小新有两根长度分别为4分米和7分米的木条,他想制作一个三角形的支架,第三根木条应选择( )。
A.3分米 B.7分米 C.11分米 D.13分米
2.下面每个选项中的3个数分别表示3条线段的长度,其中不能围成三角形的是( )。
A.3cm,4cm,5cm B.5cm,5cm,5cm
C.3cm,3cm,5cm D.6cm,6cm,12cm
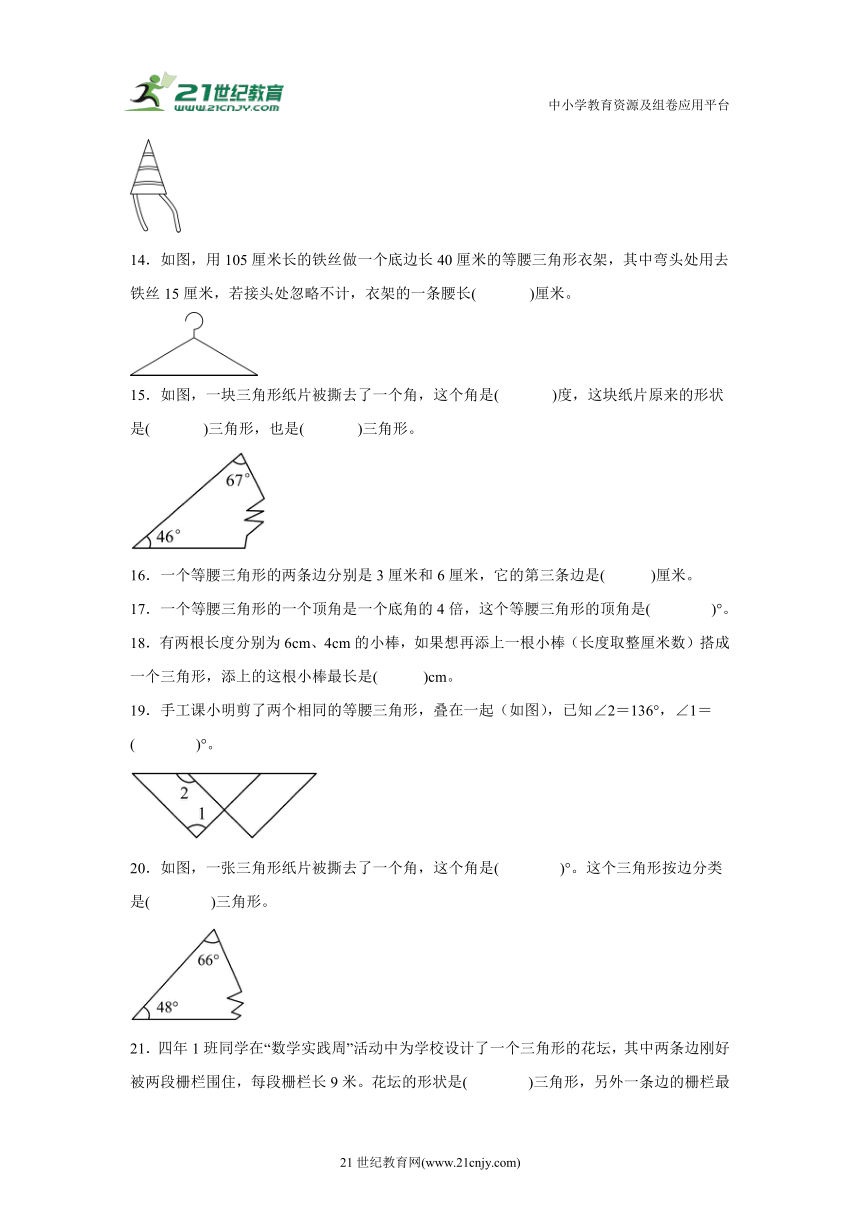
3.一扇窗户打开后,用窗钩AB可将其固定,运用到我们这学期学习的知识是( )。
A.三角形具有稳定性 B.三角形的内角和是
C.两点确定一条直线 D.三角形任意两边的和大于第三边
4.下列四组小棒,可以围成三角形的是( )。
A.1cm,4cm,5cm B.3cm,3cm,3cm
C.1cm,2cm,4cm D.2cm,2cm,6cm
5.如下图,小宇从家到学校行走的过程中,每走一步所在的位置与学校和图书馆所在的位置顺次连接都能围成一个三角形,想象一下所围成的三角形可能是( )。
A.AB B.AC C.BC D.ABC
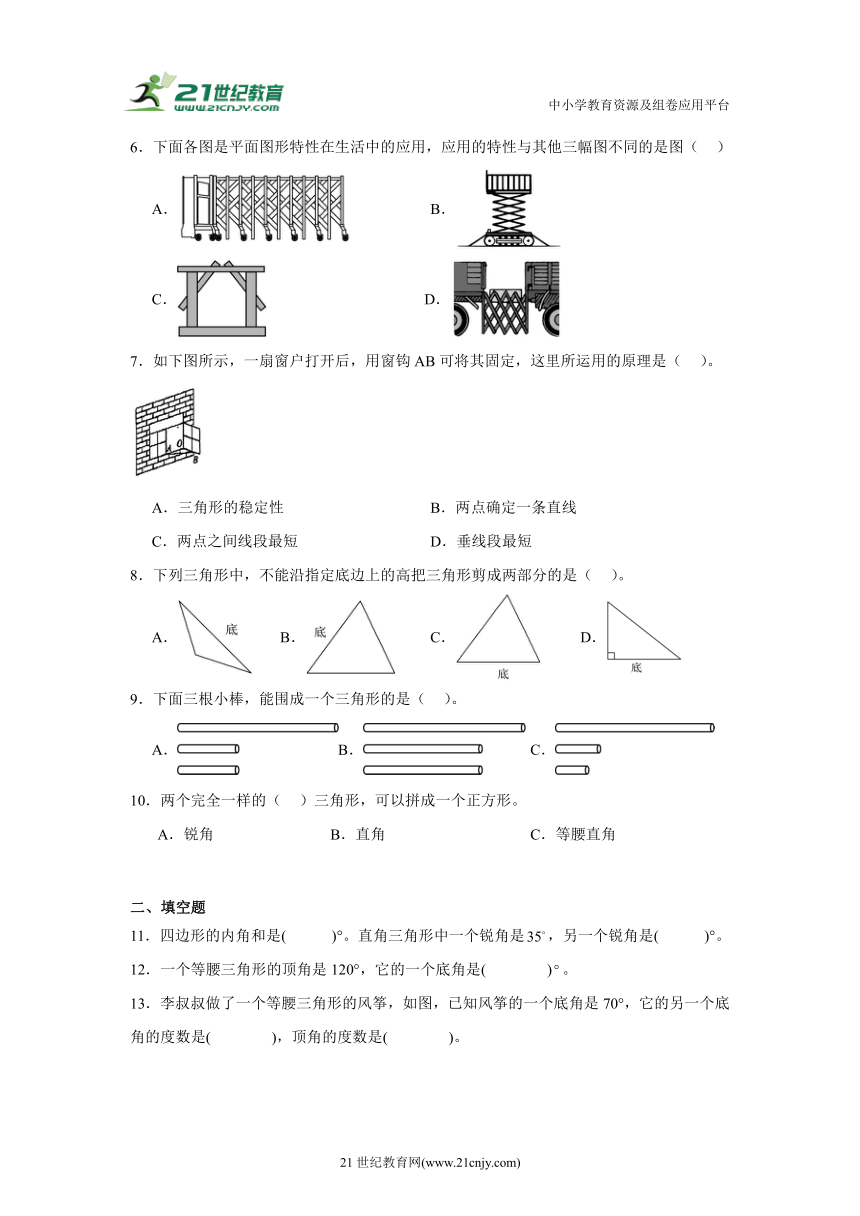
6.下面各图是平面图形特性在生活中的应用,应用的特性与其他三幅图不同的是图( )
A. B.
C. D.
7.如下图所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的原理是( )。
A.三角形的稳定性 B.两点确定一条直线
C.两点之间线段最短 D.垂线段最短
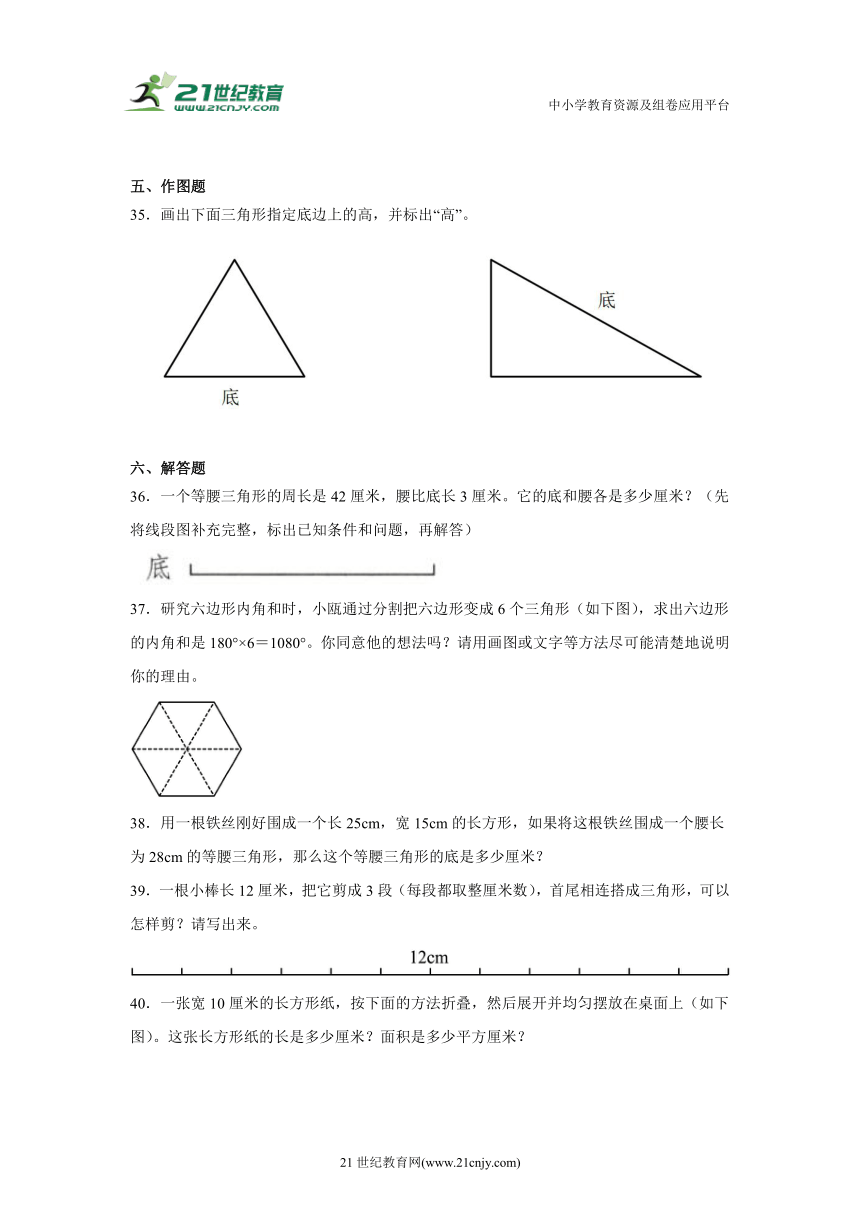
8.下列三角形中,不能沿指定底边上的高把三角形剪成两部分的是( )。
A. B. C. D.
9.下面三根小棒,能围成一个三角形的是( )。
A.B. C.
10.两个完全一样的( )三角形,可以拼成一个正方形。
A.锐角 B.直角 C.等腰直角
二、填空题
11.四边形的内角和是( )°。直角三角形中一个锐角是,另一个锐角是( )°。
12.一个等腰三角形的顶角是120°,它的一个底角是( )。
13.李叔叔做了一个等腰三角形的风筝,如图,已知风筝的一个底角是70°,它的另一个底角的度数是( ),顶角的度数是( )。
14.如图,用105厘米长的铁丝做一个底边长40厘米的等腰三角形衣架,其中弯头处用去铁丝15厘米,若接头处忽略不计,衣架的一条腰长( )厘米。
15.如图,一块三角形纸片被撕去了一个角,这个角是( )度,这块纸片原来的形状是( )三角形,也是( )三角形。
16.一个等腰三角形的两条边分别是3厘米和6厘米,它的第三条边是( )厘米。
17.一个等腰三角形的一个顶角是一个底角的4倍,这个等腰三角形的顶角是( )°。
18.有两根长度分别为6cm、4cm的小棒,如果想再添上一根小棒(长度取整厘米数)搭成一个三角形,添上的这根小棒最长是( )cm。
19.手工课小明剪了两个相同的等腰三角形,叠在一起(如图),已知∠2=136°,∠1=( )°。
20.如图,一张三角形纸片被撕去了一个角,这个角是( )°。这个三角形按边分类是( )三角形。
21.四年1班同学在“数学实践周”活动中为学校设计了一个三角形的花坛,其中两条边刚好被两段栅栏围住,每段栅栏长9米。花坛的形状是( )三角形,另外一条边的栅栏最长为( )米。(限整米数)
22.一个等腰三角形的顶角是80°,它的一个底角是( )°;如果它的底角是50°,顶角是( )°。
23.“儿童散学归来早,忙趁东风放纸鸢。”中国自古就有放风筝的习俗。爸爸给小红买了一个等腰三角形的风筝,其中一个底角是65°,这个风筝的顶角是( )°;测得风筝的两条边长分别是14dm和7dm,这个风筝的周长是( )dm。
24.将直角三角形的直角剪掉(如图),剩下的四边形中,∠1+∠2=( )°,∠4+∠5=( )°。
25.如果在一个三角形中有两个内角的度数和是90°,那么这个三角形一定是( )三角形:如果在一个直角三角形中有一个内角是45°,那么这个三角形一定是( )三角形。
三、判断题
26.有边长分别是5cm、5cm和10cm的三根小棒,小晴认为可以围成一个三角形。( )
27.如果一个三角形有2个角是锐角,那么它一定是锐角三角形。( )
28.锐角三角形任意两个锐角的和一定大于90°。( )
29.三角形任意两个内角之和大于第三个内角。( )
30.长度分别是4厘米、5厘米和9厘米的三根小棒可以围成一个三角形。( )
31.在一个三角形中,至少有两个内角是锐角。( )
32.工人用长3米、3米和7米的三根木料做成了一个三角形木架。( )
33.钝角三角形的两个锐角的和大于90°。( )
四、计算题
34.列式计算算出下面各个未知角的度数。
五、作图题
35.画出下面三角形指定底边上的高,并标出“高”。
六、解答题
36.一个等腰三角形的周长是42厘米,腰比底长3厘米。它的底和腰各是多少厘米?(先将线段图补充完整,标出已知条件和问题,再解答)
37.研究六边形内角和时,小瓯通过分割把六边形变成6个三角形(如下图),求出六边形的内角和是180°×6=1080°。你同意他的想法吗?请用画图或文字等方法尽可能清楚地说明你的理由。
38.用一根铁丝刚好围成一个长25cm,宽15cm的长方形,如果将这根铁丝围成一个腰长为28cm的等腰三角形,那么这个等腰三角形的底是多少厘米?
39.一根小棒长12厘米,把它剪成3段(每段都取整厘米数),首尾相连搭成三角形,可以怎样剪?请写出来。
40.一张宽10厘米的长方形纸,按下面的方法折叠,然后展开并均匀摆放在桌面上(如下图)。这张长方形纸的长是多少厘米?面积是多少平方厘米?
41.把一条长15cm的线段截为三段,使每条线段的长度是整厘米数,用这三条线段可以组成多少个不同的三角形?分别是哪几种情况?
42.如下图所示,文化小区有一个形状是由三个大小不同的等边三角形DMN、等边三角形MAO、等边三角形OBN组成的花园。由M地到N地,走哪条路最近?其它两条路一样长吗?为什么?
43.如图,李叔叔要估计池塘两岸A、B之间的距离,因为A、B之间有淤泥,不方便直接测量,所以李叔叔在池塘外选取一点O,测得OA=15米,OB=10米。根据以上信息,李叔叔说:“A、B之间的距离可能是25米。”你认为李叔叔说得对吗?请写出理由。
44.淘气是个爱动手、爱动脑的孩子。他把一根20厘米长的吸管剪成3段(每段长是整厘米数),再用这三段吸管围成一个等腰三角形,可以怎么剪?(写出三种不同的答案,可画图说明)
45.亮亮准备用铁丝围成一个等腰三角形框架,这个等腰三角形框架的两条边分别是7厘米和11厘米。
(1)有几种围法?画图表示出来。
(2)围这样一个等腰三角形框架,至少需要多少厘米长的铁丝?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.B
【分析】本题可根据三角形三边关系“任意两边之和大于第三边,任意两边之差小于第三边”来确定第三根木条长度的取值范围,进而判断各选项是否符合要求。已知两根木条长度分别为4分米和7分米。根据三角形三边关系,第三边的长度应大于两边之差,小于两边之和。两边之差为7-4=3(分米),两边之和为7+4=11(分米),所以第三根木条的长度范围是大于3分米且小于11分米。
【解析】A.3分米不满足大于3分米的条件,所以A选项错误;
B.7分米在大于3分米且小于11分米的范围内,所以B选项正确;
C.11分米不满足小于11分米的条件,所以C选项错误;
D.13分米不满足小于11分米的条件,所以D选项错误。
所以,第三根木条应选择7分米;
故答案为:B
2.D
【分析】根据三角形的三边关系,三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【解析】A.3+4=7(cm),7>5,3+5=8(cm),8>4,4+5=9(cm),9>3,能组成三角形;所以不符合题意;
B.5+5=10(cm),10>5,能组成三角形;所以不符合题意;
C.3+3=6(cm),6>5,3+5=8(cm),8>3,能组成三角形;所以不符合题意;
D.6+6=12(cm),12=12,不能组成三角形;所以符合题意。
故答案为:D
3.A
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性;据此进行解答。
【解析】由分析可知,一扇窗户打开后,用窗钩AB可将其固定,所运用的知识是三角形的稳定性。
故答案为:A
4.B
【分析】根据三角形的任意两边之和大于第三边,据此判断是否可以围成三角形。
【解析】A.1cm,4cm,5cm,1+4=5,5=5,不满足两边之和大于第三边,无法围成三角形;
B.3cm,3cm,3cm,3+3=6,6>3,满足两边之和大于第三边,可以围成三角形;
C.1cm,2cm,4cm,1+2=3,3<4,不满足两边之和大于第三边,无法围成三角形;
D.2cm,2cm,6cm,2+2=4,4<6,不满足两边之和大于第三边,无法围成三角形。
故答案为:B
5.D
【分析】三个角都是锐角的三角形叫做锐角三角形,有一个直角的三角形叫做直角三角形,有一个角是钝角的三角形叫做钝角三角形。据此可知,任何一个三角形都至少有2个锐角,题目只明确了一个内角是60°,那么这个三角形三种情况都有可能。据此解答。
【解析】由分析得:
如果图书馆到小宇家的那条边与小宇家到学校的那条边围成的夹角是锐角,这个三角形是锐角三角形。若这个夹角是直角,这个三角形是直角三角形,若这个三角形是钝角,这个三角形是钝角三角形。
故答案为:D
6.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性;据此进行解答。
【解析】A.伸缩门应用了平行四边形的不稳定性;
B.伸缩机应用了平行四边形的不稳定性;
C.框架应用了三角形的稳定性;
D.伸缩连接应用了平行四边形的不稳定性;
故答案为:C
7.A
【分析】从图中可知,用窗钩AB将打开的窗户固定后,窗钩与窗户和窗框之间构成了三角形(如下图),因三角形具有稳定性,不容易变形,这样使窗户的位置不容易发生变化,从而固定了窗户;据此解答。
【解析】根据分析可知:
一扇窗户打开后,用窗钩AB可将其固定,这里所运用的原理是:三角形的稳定性。
故答案为:A
8.D
【分析】根据题意,画出三角形的高即可判断。
【解析】
A. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
B. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
C. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
D. 直角三角形直角边上的高就是与它垂直的另一条直角边,因此不能把三角形分成两部分,符合题意。
故答案为:D
9.B
【分析】根据题意,三角形任意两边之和大于第三边,据此判断选择即可。
【解析】
A.下面两根小棒的加起来比上面的短,不能围成三角形。
B.,可以围成三角形。
C.下面两根小棒的加起来比上面的短,不能围成三角形。
故答案为:B
10.C
【分析】根据题意,正方形的四条边都相等,四个角都是直角,所以两个三角形的样子一定是两条边相等,且有一个角是直角,才可拼成一个正方形,如图:正方形沿着对角线剪开后是两个完全相同的等腰直角三角形,等腰直角三角形是有一个角为直角且两腰相等的三角形,据此解答即可。
【解析】根据分析可知:
两个完全一样的等腰直角三角形,可以拼成一个正方形。
故答案为:C
11.360 55
【分析】根据题意,任意四边形(如正方形、长方形等)的四个内角之和等于360°。直角三角形中有一个直角90°,其余两个锐角之和为90°。已知一个锐角是35°,则另一个锐角为90°-35°=55°;以此答题即可。
【解析】根据分析可知:
90°-35°=55°
四边形的内角和是360°。直角三角形中一个锐角是,另一个锐角是55°。
12.30
【分析】等腰三角形两个底角相等,根据三角形内角和为180°,用180°减去顶角度数,然后用所得的结果除以2,据此计算可求出一个底角的度数。
【解析】(180°-120°)÷2
=60°÷2
=30°
综上可知,它的一个底角是30°。
13.70°/70度 40°/40度
【分析】由题意可知,等腰三角形的两个底角相等都是70°,三角形的内角和是180°,那么顶角的度数就是内角和减去2个底角的度数,列式为180°-70°×2。
【解析】180°-70°×2
=180°-140°
=40°
李叔叔做了一个等腰三角形的风筝,如图,已知风筝的一个底角是70°,它的另一个底角的度数是70°,顶角的度数是40°。
14.25
【分析】用105减去弯头处的长度,剩下的就是三角形的周长,然后根据等腰三角形的两条腰相等;用三角形的周长减去底边长度,将所得的差再除以2,据此计算可得出衣架的一条腰长多少。
【解析】105-15=90(厘米)
(90-40)÷2
=50÷2
=25(厘米)
综上可知,衣架的一条腰长25厘米。
15.67 锐角/等腰 等腰/锐角
【分析】根据题意,三角形的内角和是180°,用180°减去67°减去46°就是撕去的那个角的度数。,三个角都是锐角的三角形是锐角三角形。有两个角相等的三角形是等腰三角形。据此判断形状即可。
【解析】180°-67°-46°
=113°-46°
=67°
一块三角形纸片被撕去了一个角,这个角是67度。
因为67°、67°、46°都是锐角,67°=67°所以这块纸片原来的形状是锐角(等腰)三角形,也是等腰(锐角)三角形。
16.
6
【分析】等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此确定出这个等腰三角形的第三条边长。
【解析】3厘米+3厘米=6厘米,因此第三条边长不能为3厘米;
6厘米+6厘米>3厘米,6厘米-3厘米<6厘米,
因此第三条边长是6厘米。
17.120
【分析】根据三角形三个内角的度数和是180°,等腰三角形两个底角度数相等,把一个底角看作1份,则顶角是1×4=4(份),所以三个角的度数和就是1+1+4=6(份),用180°除以总份数6,即得到每份数一个底角的度数,再乘4即得到顶角的度数。据此解答。
【解析】1+1+4=6(份)
180°÷6=30°
30°×4=120°
即一个等腰三角形的一个顶角是一个底角的4倍,这个等腰三角形的顶角是120°。
18.
9
【分析】根据题意,根据三角形三边关系,第三边必须大于两边之差且小于两边之和。已知两根小棒分别为6厘米和4厘米,第三边长度需满足:6-4<第三边<6+4,即2<第三边<10。由于长度取整厘米数,第三边最长为9厘米。以此答题即可。
【解析】根据分析可知:
6-4=2(厘米)
6+4=10(厘米)
10-1=9(厘米)
有两根长度分别为6cm、4cm的小棒,如果想再添上一根小棒(长度取整厘米数)搭成一个三角形,添上的这根小棒最长是9cm。
19.92
【分析】
已知∠2=136°,∠3和∠2组成一个平角,用180°-136°=44°,求出∠3的度数,等腰三角形两个底角度数相等,∠3=∠4,三角形内角和等于180°,用180°―44°―44°,求出∠5的度数,由图形可知∠5=∠1,据此即可求出∠1的度数。
【解析】180°-136°=44°
180°―44°―44°
=136°―44°
=92°
因此,∠1=92°。
20.66 等腰
【分析】三角形按边来分,分为不等边三角形、等腰三角形和等边三角形。有两条边相等的三角形叫作等腰三角形,等腰三角形的两个底角相等。三条边都相等的三角形叫作等边三角形,等边三角形的三个角都相等。
由题意得,一张三角形纸片的两个角分别是66°、48°,三角形的内角和为180°,那么直接用180°减去两个内角的度数即可算出第三个角的度数。然后根据三个角的大小来判断三角形的类型即可。
【解析】180°-48°-66°=66°
这个三角形中有两个角都是66°,这个三角形按边分类是等腰三角形。
如图,一张三角形纸片被撕去了一个角,这个角是66°。这个三角形按边分类是等腰三角形。
21.等腰 17
【分析】一个三角形的花坛,其中两条边刚好被两段栅栏围住,说明两条边的长度相等,两条边长都是9米,等腰三角形两条腰相等,那么这是一个等腰三角形花坛;根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,据此即可求出另外一条边的栅栏最长为米。
【解析】9+9=18(米)
第三边<18米
第三边最长是18-1=17(米)
因此,这个花坛的形状是等腰三角形,另外一条边的栅栏最长为17米。
22.50 80
【分析】三角形的内角和等于180°,等腰三角形的两底角相等,用180°减去顶角的80°等于两个底角的度数和,再除以2即等于一个底角的度数;等腰三角形的底角等于50°,用180°减去两个50°即等于顶角的度数;据此即可解答。
【解析】(180°-80°)÷2
=100°÷2
=50°
180°-50°-50°
=130°-50°
=80°
即,一个等腰三角形的顶角是80°,它的一个底角是50°;如果它的底角是50°,顶角是80°。
23.50 35
【分析】(1)三角形的内角和是180°,等腰三角形的两个底角相等,求顶角的度数,用180°减去两个底角的度数即可解答;
(2)等腰三角形的两个腰相等,测得的两条边是14分米和7分米,不知道哪条边是腰,哪条边是底边,因此需要分类讨论;
当14分米为底边时,那么7分米就是等腰三角形的腰,此时等腰三角形的三边分别为7分米、7分米、14分米,因为7+7=14,三角形的两边之和要大于第三边,所以这个等腰三角形的三边不可能是7分米、7分米、14分米;三条边的长只能是14分米、14分米、7分米,求三角形的周长,把三条边相加即可。
【解析】180°-65°-65°=50°
所以这个风筝的顶角是50°。
14+14+7=35(分米)
所以这个风筝的周长是35分米。
24.90 270
【分析】三角形的内角和为180°,四边形的内角和为360°。
原来的直角三角形中,∠1、∠2和一个直角组成一个三角形,用三角形的内角和减去90°,即可求出∠1与∠2的度数之和。
∠1、∠2、∠4、∠5组成一个四边形,用四边形的内角和减去∠1与∠2的度数之和,即是∠4与∠5的度数之和。
【解析】∠1+∠2=180°-90°=90°
∠4+∠5=360°-(∠1+∠2)=360°-90°=270°
即∠1+∠2=90°,∠4+∠5=270°。
25.直角 等腰直角/等腰
【分析】根据题意,明确三角形内角和是180°,已知三角形中有两个内角的度数和是90°,那么用180°减去90°,就可以求出第三个角的度数;三角形按角分为锐角三角形(三个角均小于90°)、直角三角形(一个角为90°)和钝角三角形(一个角大于90°)。可以判断这个三角形一定是直角三角形。在直角三角形中,已经有一个角是90°,如果还有一个内角是45°,那么第三个角的度数就是:用180°减去90°,再减去45°,可知求出第三个角的度数是45°;两个锐角相等,这个三角形有两条边相等(等腰),且有一个直角。因此,它一定是等腰直角三角形。
【解析】根据分析可知:
180°-90°=90°
180°-90°-45°=45°
如果在一个三角形中有两个内角的度数和是90°,那么这个三角形一定是直角三角形:如果在一个直角三角形中有一个内角是45°,那么这个三角形一定是等腰直角三角形。
26.
×
【分析】根据三角形三边关系,任意两边之和必须大于第三边。题目中较短的两边之和为(cm),等于最长边10cm,不满足“两边之和大于第三边”的条件,因此无法围成三角形,据此解答。
【解析】较短两边之和:(cm)
比较两边之和与最长边:10cm=10cm。
所以5cm、5cm和10cm的三根小棒无法构成三角形。
故答案为:×
27.
×
【分析】根据三角形内角和定理,三个角的和为180°。若一个三角形有两个锐角,第三个角可能是锐角、直角或钝角,因此三角形可能是锐角三角形、直角三角形或钝角三角形。
【解析】假设两个锐角均为45°,则第三个角为,此时为直角三角形;
若两个锐角均为80°,则第三个角为,此时为锐角三角形;
若两个锐角均为30°,则第三个角为,此时为钝角三角形。
因此,有两个锐角的三角形不一定是锐角三角形;
故答案为:×
28.√
【分析】锐角三角形的意义:三个角都小于90°的三角形。三角形内角和是180°;由此可知,任意两个锐角的度数和加第3个角的度数和是180°,由于第3个角是锐角,所以第3个角的度数小于90°,那么任意两个锐角的和一定大于90°,据此解答。
【解析】根据分析可知,锐角三角形任意两个锐角的和一定大于90°,原题干说法正确。
故答案为:√
29.×
【分析】三个角都是锐角的三角形叫作锐角三角形。有一个角是直角的三角形叫作直角三角形。有一个角是钝角的三角形叫作钝角三角形。三角形的内角和为180°。据此解答。
【解析】根据题意作图如下:
在锐角三角形中,60°+60°=120°。120°>60°,满足题意。在直角三角形中,60°+30°=90°。90°=90°,不满足题意。在钝角三角形中,30°+30°=60°。60°<120°,不满足题意。原题说法错误。
故答案为:×
30.×
【分析】三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。
【解析】4+5=9(厘米),9厘米=9厘米,即这三根小棒无法围成三角形。原题说法错误。
故答案为:×
31.√
【分析】根据三角形内角和可知,三角形的三个内角之和为180°。假设一个三角形中只有一个锐角,即可得出结论,据此解答。
【解析】假设一个三角形中只有一个锐角,则另外两个角都大于或等于90°,此时三个角的和必然超过180°,与三角形内角和是180°矛盾;原说法正确。
故答案为:√
32.×
【分析】根据三角形的三边关系,任意两边之和必须大于第三边。据此判断。
【解析】3+7>3,3+3<7,存在两边之和小于第三边的情况。故3米、3米和7米的三根木料不能做成一个三角形木架。原题表述错误。
故答案为:×
33.×
【分析】钝角三角形有一个角大于90°,另外两个角为锐角。根据三角形内角和为180°,钝角的度数大于90°,因此另外两个锐角的和必然小于90°。据此判断。
【解析】例如,若钝角为100°,则两锐角和为80°;若钝角为120°,则两锐角和为60°,均小于90°。
因此钝角三角形的两个锐角的和小于90°。题干说法错误。
故答案为:×
34.78°;60°
【分析】根据三角形内角和是180°和图中给出的度数,用180°减去三角形的两个已知角度,可以求得未知角的度数。
【解析】根据分析可知:
180°-(65°+37°)
=180°-102°
= 78°
图一的未知角的度数是 78°。
180°-(90°+30°)
=180°-120°
= 60°
图二的未知角的度数是 60°。
35.见详解
【分析】从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高,这个顶点所对的边叫做三角形的底。据此作图。
【解析】
36.底12厘米;腰15厘米
【分析】等腰三角形的两腰相等,两条腰长加上底的长度就是它的周长。根据周长是42厘米,腰比底长3厘米。画出线段图即可。
用它的周长减去2个3厘米的长度就是3个底的长度。算出结果除以3就是一条底的长度。再用底的长度加上3厘米就是腰的长度。
【解析】根据条件,画出的线段图如下所示:
底长:
(42-2×3)÷3
=(42-6)÷3
=36÷3
=12(厘米)
腰长:12+3=15(厘米)
答:它的底是12厘米和腰是15厘米。
37.不同意;理由见详解
【分析】求多边形的内角和,可以看这个多边形可以分成几个三角形,三角形的内角和为180°,直接用180°乘可以分成三角形的个数即可算出多边形的内角和。由题意得,小瓯把六边形变成6个三角形。这样分割时把中间的周角也分给了6个三角形,这个周角原本不是六边形的内角,所以最后算出来的结果会比正确的结果多一个周角的度数。
【解析】答:不同意小瓯的方法。因为这样分割把中间6个角的度数和也算进去了,也就是多算了一个周角的度数,正确的度数应该等于1080°减去360°。
38.24厘米
【分析】根据题意,长方形的周长=(长+宽)×2,已知用一根铁丝刚好围成一个长25cm,宽15cm的长方形,先求出铁丝的长度;又知等腰三角形的两腰相等,用铁丝的长度减去两个28,就是这个等腰三角形的底的长度;列式计算即可。
【解析】根据分析可知:
(25+15)×2
=40×2
=80(厘米)
80-28-28
=52-28
=24(厘米)
答:这个等腰三角形的底是24厘米。
39.5厘米,3厘米和4厘米;5厘米,5厘米和2厘米;4厘米,4厘米和4厘米
【分析】三角形两边之和大于第三边,两边之差小于第三边;三角形中三边和等于12厘米, 据此写出所以情况即可解题。
【解析】12=5+3+4;5+3=8(厘米);8厘米>4厘米;
12=5+2+5;5+2=7(厘米);7厘米>5厘米;
12=4+4+4;4+4=8(厘米);8厘米>4厘米;
答:可以剪成三角形的边长分别是5厘米,3厘米和4厘米;5厘米,5厘米和2厘米;4厘米,4厘米和4厘米。
40.60厘米;600平方厘米
【分析】仔细观察发现展开后纸与桌面形成一些等边三角形。等边三角形三条边长都相等,测量展开后的长度是30厘米,那么这张纸原本的长度是30×2=60(厘米),长方形的面积=长×宽,据此计算。
【解析】30×2=60(厘米)
60×10=600(平方厘米)
答:这张长方形纸的长是60厘米,面积是600平方厘米。
41.7个;见解析
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。14÷2=71,截出的三条线段的最大边最大是7厘米,最小是5厘米,由此进行推理归纳即可得出结论。
【解析】根据分析可知:
最大边为7厘米时,另两边之和为8厘米。
1+7=8(厘米)三边分别为:7厘米、7厘米、1厘米
2+6=8(厘米)三边分别为:7厘米、2厘米、6厘米
3+5=8(厘米)三边分别为:7厘米、3厘米、5厘米
4+4=8(厘米)三边分别为:7厘米、4厘米、4厘米
可构成4个不同的三角形。
最大边为6厘米时,另两边之和为9厘米。
3+6=9(厘米) 三边分别为:6厘米、3厘米、6厘米
4+5=9(厘米)三边分别为:6厘米、4厘米、5厘米
可构成2个不同的三角形。
最大边为5厘米时,另两边之和为10厘米。
5+5=10(厘米)三边分别为:5厘米、5厘米、5厘米
可构成1个不同的三角形。
4+2+1=7(个)
答:用这三条线段可以组成7个不同的三角形。
42.沿MN走最近;一样长;见详解
【分析】等边三角形的三条边长度相等。由题意得,从M到N,沿着MN走是最近的,因为两点之间线段是最短的;第二问,可以根据等边三角形的特征判断出各个线段长度之间的关系。
【解析】沿MN走最近,MN=80米。因为三个三角形都是大小不同的等边三角形,所以MD=ND=MO+ON,MO=MA=OA,OB=ON=BN。所以MD+DN=MN×2=(50+30)×2=80×2=160(米),MA+AO+OB+BN=MO×2+ON×2=50×2+30×2=100+60=160(米)。160=160,所以其它两条路一样长。
答:沿MN走最近且其它两条路一样长。
43.不对;理由见详解
【分析】根据题意,连接O、A、B这三点围成一个三角形,三角形任意两边的和大于第三条边。据此解答即可。
【解析】李叔叔说得不对。因为三角形任意两边的和大于第三边,所以OA+OB的长度应该大于AB的长度,15+10=25(米),A、B之间的距离应该比25米小,不可能是25米。
44.见详解
【分析】有两条边相等的三角形叫作等腰三角形。三角形三边的关系:任意两边之和大于第三边,任意两边之差小于第三边。由题意得,淘气要把一根20厘米长的吸管剪成3段(每段长是整厘米数),再用这三段吸管围成一个等腰三角形,那么这三段应该有两段的长度应该相等且满足构成三角形的条件。据此解答。
【解析】6+6+8=12+8=20(厘米),6=6,6+6=12>8,即淘气可以将吸管剪成6厘米,6厘米,8厘米的小段。
7+7+6=14+6=20(厘米),7=7,6+7=13>7,即淘气可以将吸管剪成7厘米,7厘米,6厘米的小段。
8+8+4=16+4=20(厘米),8=8,8+4=12>8,即淘气可以将吸管剪成8厘米,8厘米,4厘米的小段。
答:淘气可以将吸管剪成6厘米,6厘米,8厘米的小段,也可以将吸管剪成7厘米,7厘米,6厘米的小段,还可以将吸管剪成8厘米,8厘米,4厘米的小段。(答案不唯一)
45.(1)有两种围法;见详解
(2)25厘米
【分析】(1)已知这个等腰三角形框架的两条边分别是7厘米和11厘米,根据等腰三角形有两条相等的边和一条底边,我们需要考虑两种情况:①两条相等的边为7厘米,底边为11厘米。②两条相等的边为11厘米,底边为7厘米。再根据三角形的三边关系:三角形三边之和大于第三边,进行判断即可。
(2)把三角形的三条边相加,分别求出两种围法三角形的周长,然后取较小的值即可。
【解析】(1)两种情况:
①两条相等的边为7厘米,底边为11厘米。
7+7=14(厘米);14厘米>11厘米
7+11=18(厘米);18厘米>7厘米
因此两条相等的边为7厘米,底边为11厘米可以围成一个三角形。
②两条相等的边为11厘米,底边为7厘米。
11+11=22(厘米),22厘米>7厘米
7+11=18(厘米);18厘米>11厘米
因此两条相等的边为7厘米,底边为11厘米可以围成一个三角形。
综上可知,有两种围法。
画图如下:
(2)11+11+7=29(厘米)
7+7+11=25(厘米)
25<29
答:至少需要25厘米长的铁丝。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2025年数学四升五暑假巩固培优精练(人教版)
专题05 是三角形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小新有两根长度分别为4分米和7分米的木条,他想制作一个三角形的支架,第三根木条应选择( )。
A.3分米 B.7分米 C.11分米 D.13分米
2.下面每个选项中的3个数分别表示3条线段的长度,其中不能围成三角形的是( )。
A.3cm,4cm,5cm B.5cm,5cm,5cm
C.3cm,3cm,5cm D.6cm,6cm,12cm
3.一扇窗户打开后,用窗钩AB可将其固定,运用到我们这学期学习的知识是( )。
A.三角形具有稳定性 B.三角形的内角和是
C.两点确定一条直线 D.三角形任意两边的和大于第三边
4.下列四组小棒,可以围成三角形的是( )。
A.1cm,4cm,5cm B.3cm,3cm,3cm
C.1cm,2cm,4cm D.2cm,2cm,6cm
5.如下图,小宇从家到学校行走的过程中,每走一步所在的位置与学校和图书馆所在的位置顺次连接都能围成一个三角形,想象一下所围成的三角形可能是( )。
A.AB B.AC C.BC D.ABC
6.下面各图是平面图形特性在生活中的应用,应用的特性与其他三幅图不同的是图( )
A. B.
C. D.
7.如下图所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的原理是( )。
A.三角形的稳定性 B.两点确定一条直线
C.两点之间线段最短 D.垂线段最短
8.下列三角形中,不能沿指定底边上的高把三角形剪成两部分的是( )。
A. B. C. D.
9.下面三根小棒,能围成一个三角形的是( )。
A.B. C.
10.两个完全一样的( )三角形,可以拼成一个正方形。
A.锐角 B.直角 C.等腰直角
二、填空题
11.四边形的内角和是( )°。直角三角形中一个锐角是,另一个锐角是( )°。
12.一个等腰三角形的顶角是120°,它的一个底角是( )。
13.李叔叔做了一个等腰三角形的风筝,如图,已知风筝的一个底角是70°,它的另一个底角的度数是( ),顶角的度数是( )。
14.如图,用105厘米长的铁丝做一个底边长40厘米的等腰三角形衣架,其中弯头处用去铁丝15厘米,若接头处忽略不计,衣架的一条腰长( )厘米。
15.如图,一块三角形纸片被撕去了一个角,这个角是( )度,这块纸片原来的形状是( )三角形,也是( )三角形。
16.一个等腰三角形的两条边分别是3厘米和6厘米,它的第三条边是( )厘米。
17.一个等腰三角形的一个顶角是一个底角的4倍,这个等腰三角形的顶角是( )°。
18.有两根长度分别为6cm、4cm的小棒,如果想再添上一根小棒(长度取整厘米数)搭成一个三角形,添上的这根小棒最长是( )cm。
19.手工课小明剪了两个相同的等腰三角形,叠在一起(如图),已知∠2=136°,∠1=( )°。
20.如图,一张三角形纸片被撕去了一个角,这个角是( )°。这个三角形按边分类是( )三角形。
21.四年1班同学在“数学实践周”活动中为学校设计了一个三角形的花坛,其中两条边刚好被两段栅栏围住,每段栅栏长9米。花坛的形状是( )三角形,另外一条边的栅栏最长为( )米。(限整米数)
22.一个等腰三角形的顶角是80°,它的一个底角是( )°;如果它的底角是50°,顶角是( )°。
23.“儿童散学归来早,忙趁东风放纸鸢。”中国自古就有放风筝的习俗。爸爸给小红买了一个等腰三角形的风筝,其中一个底角是65°,这个风筝的顶角是( )°;测得风筝的两条边长分别是14dm和7dm,这个风筝的周长是( )dm。
24.将直角三角形的直角剪掉(如图),剩下的四边形中,∠1+∠2=( )°,∠4+∠5=( )°。
25.如果在一个三角形中有两个内角的度数和是90°,那么这个三角形一定是( )三角形:如果在一个直角三角形中有一个内角是45°,那么这个三角形一定是( )三角形。
三、判断题
26.有边长分别是5cm、5cm和10cm的三根小棒,小晴认为可以围成一个三角形。( )
27.如果一个三角形有2个角是锐角,那么它一定是锐角三角形。( )
28.锐角三角形任意两个锐角的和一定大于90°。( )
29.三角形任意两个内角之和大于第三个内角。( )
30.长度分别是4厘米、5厘米和9厘米的三根小棒可以围成一个三角形。( )
31.在一个三角形中,至少有两个内角是锐角。( )
32.工人用长3米、3米和7米的三根木料做成了一个三角形木架。( )
33.钝角三角形的两个锐角的和大于90°。( )
四、计算题
34.列式计算算出下面各个未知角的度数。
五、作图题
35.画出下面三角形指定底边上的高,并标出“高”。
六、解答题
36.一个等腰三角形的周长是42厘米,腰比底长3厘米。它的底和腰各是多少厘米?(先将线段图补充完整,标出已知条件和问题,再解答)
37.研究六边形内角和时,小瓯通过分割把六边形变成6个三角形(如下图),求出六边形的内角和是180°×6=1080°。你同意他的想法吗?请用画图或文字等方法尽可能清楚地说明你的理由。
38.用一根铁丝刚好围成一个长25cm,宽15cm的长方形,如果将这根铁丝围成一个腰长为28cm的等腰三角形,那么这个等腰三角形的底是多少厘米?
39.一根小棒长12厘米,把它剪成3段(每段都取整厘米数),首尾相连搭成三角形,可以怎样剪?请写出来。
40.一张宽10厘米的长方形纸,按下面的方法折叠,然后展开并均匀摆放在桌面上(如下图)。这张长方形纸的长是多少厘米?面积是多少平方厘米?
41.把一条长15cm的线段截为三段,使每条线段的长度是整厘米数,用这三条线段可以组成多少个不同的三角形?分别是哪几种情况?
42.如下图所示,文化小区有一个形状是由三个大小不同的等边三角形DMN、等边三角形MAO、等边三角形OBN组成的花园。由M地到N地,走哪条路最近?其它两条路一样长吗?为什么?
43.如图,李叔叔要估计池塘两岸A、B之间的距离,因为A、B之间有淤泥,不方便直接测量,所以李叔叔在池塘外选取一点O,测得OA=15米,OB=10米。根据以上信息,李叔叔说:“A、B之间的距离可能是25米。”你认为李叔叔说得对吗?请写出理由。
44.淘气是个爱动手、爱动脑的孩子。他把一根20厘米长的吸管剪成3段(每段长是整厘米数),再用这三段吸管围成一个等腰三角形,可以怎么剪?(写出三种不同的答案,可画图说明)
45.亮亮准备用铁丝围成一个等腰三角形框架,这个等腰三角形框架的两条边分别是7厘米和11厘米。
(1)有几种围法?画图表示出来。
(2)围这样一个等腰三角形框架,至少需要多少厘米长的铁丝?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.B
【分析】本题可根据三角形三边关系“任意两边之和大于第三边,任意两边之差小于第三边”来确定第三根木条长度的取值范围,进而判断各选项是否符合要求。已知两根木条长度分别为4分米和7分米。根据三角形三边关系,第三边的长度应大于两边之差,小于两边之和。两边之差为7-4=3(分米),两边之和为7+4=11(分米),所以第三根木条的长度范围是大于3分米且小于11分米。
【解析】A.3分米不满足大于3分米的条件,所以A选项错误;
B.7分米在大于3分米且小于11分米的范围内,所以B选项正确;
C.11分米不满足小于11分米的条件,所以C选项错误;
D.13分米不满足小于11分米的条件,所以D选项错误。
所以,第三根木条应选择7分米;
故答案为:B
2.D
【分析】根据三角形的三边关系,三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【解析】A.3+4=7(cm),7>5,3+5=8(cm),8>4,4+5=9(cm),9>3,能组成三角形;所以不符合题意;
B.5+5=10(cm),10>5,能组成三角形;所以不符合题意;
C.3+3=6(cm),6>5,3+5=8(cm),8>3,能组成三角形;所以不符合题意;
D.6+6=12(cm),12=12,不能组成三角形;所以符合题意。
故答案为:D
3.A
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性;据此进行解答。
【解析】由分析可知,一扇窗户打开后,用窗钩AB可将其固定,所运用的知识是三角形的稳定性。
故答案为:A
4.B
【分析】根据三角形的任意两边之和大于第三边,据此判断是否可以围成三角形。
【解析】A.1cm,4cm,5cm,1+4=5,5=5,不满足两边之和大于第三边,无法围成三角形;
B.3cm,3cm,3cm,3+3=6,6>3,满足两边之和大于第三边,可以围成三角形;
C.1cm,2cm,4cm,1+2=3,3<4,不满足两边之和大于第三边,无法围成三角形;
D.2cm,2cm,6cm,2+2=4,4<6,不满足两边之和大于第三边,无法围成三角形。
故答案为:B
5.D
【分析】三个角都是锐角的三角形叫做锐角三角形,有一个直角的三角形叫做直角三角形,有一个角是钝角的三角形叫做钝角三角形。据此可知,任何一个三角形都至少有2个锐角,题目只明确了一个内角是60°,那么这个三角形三种情况都有可能。据此解答。
【解析】由分析得:
如果图书馆到小宇家的那条边与小宇家到学校的那条边围成的夹角是锐角,这个三角形是锐角三角形。若这个夹角是直角,这个三角形是直角三角形,若这个三角形是钝角,这个三角形是钝角三角形。
故答案为:D
6.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性;据此进行解答。
【解析】A.伸缩门应用了平行四边形的不稳定性;
B.伸缩机应用了平行四边形的不稳定性;
C.框架应用了三角形的稳定性;
D.伸缩连接应用了平行四边形的不稳定性;
故答案为:C
7.A
【分析】从图中可知,用窗钩AB将打开的窗户固定后,窗钩与窗户和窗框之间构成了三角形(如下图),因三角形具有稳定性,不容易变形,这样使窗户的位置不容易发生变化,从而固定了窗户;据此解答。
【解析】根据分析可知:
一扇窗户打开后,用窗钩AB可将其固定,这里所运用的原理是:三角形的稳定性。
故答案为:A
8.D
【分析】根据题意,画出三角形的高即可判断。
【解析】
A. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
B. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
C. 如图,沿三角形的高可以把三角形分成两部分,所以不符合题意;
D. 直角三角形直角边上的高就是与它垂直的另一条直角边,因此不能把三角形分成两部分,符合题意。
故答案为:D
9.B
【分析】根据题意,三角形任意两边之和大于第三边,据此判断选择即可。
【解析】
A.下面两根小棒的加起来比上面的短,不能围成三角形。
B.,可以围成三角形。
C.下面两根小棒的加起来比上面的短,不能围成三角形。
故答案为:B
10.C
【分析】根据题意,正方形的四条边都相等,四个角都是直角,所以两个三角形的样子一定是两条边相等,且有一个角是直角,才可拼成一个正方形,如图:正方形沿着对角线剪开后是两个完全相同的等腰直角三角形,等腰直角三角形是有一个角为直角且两腰相等的三角形,据此解答即可。
【解析】根据分析可知:
两个完全一样的等腰直角三角形,可以拼成一个正方形。
故答案为:C
11.360 55
【分析】根据题意,任意四边形(如正方形、长方形等)的四个内角之和等于360°。直角三角形中有一个直角90°,其余两个锐角之和为90°。已知一个锐角是35°,则另一个锐角为90°-35°=55°;以此答题即可。
【解析】根据分析可知:
90°-35°=55°
四边形的内角和是360°。直角三角形中一个锐角是,另一个锐角是55°。
12.30
【分析】等腰三角形两个底角相等,根据三角形内角和为180°,用180°减去顶角度数,然后用所得的结果除以2,据此计算可求出一个底角的度数。
【解析】(180°-120°)÷2
=60°÷2
=30°
综上可知,它的一个底角是30°。
13.70°/70度 40°/40度
【分析】由题意可知,等腰三角形的两个底角相等都是70°,三角形的内角和是180°,那么顶角的度数就是内角和减去2个底角的度数,列式为180°-70°×2。
【解析】180°-70°×2
=180°-140°
=40°
李叔叔做了一个等腰三角形的风筝,如图,已知风筝的一个底角是70°,它的另一个底角的度数是70°,顶角的度数是40°。
14.25
【分析】用105减去弯头处的长度,剩下的就是三角形的周长,然后根据等腰三角形的两条腰相等;用三角形的周长减去底边长度,将所得的差再除以2,据此计算可得出衣架的一条腰长多少。
【解析】105-15=90(厘米)
(90-40)÷2
=50÷2
=25(厘米)
综上可知,衣架的一条腰长25厘米。
15.67 锐角/等腰 等腰/锐角
【分析】根据题意,三角形的内角和是180°,用180°减去67°减去46°就是撕去的那个角的度数。,三个角都是锐角的三角形是锐角三角形。有两个角相等的三角形是等腰三角形。据此判断形状即可。
【解析】180°-67°-46°
=113°-46°
=67°
一块三角形纸片被撕去了一个角,这个角是67度。
因为67°、67°、46°都是锐角,67°=67°所以这块纸片原来的形状是锐角(等腰)三角形,也是等腰(锐角)三角形。
16.
6
【分析】等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此确定出这个等腰三角形的第三条边长。
【解析】3厘米+3厘米=6厘米,因此第三条边长不能为3厘米;
6厘米+6厘米>3厘米,6厘米-3厘米<6厘米,
因此第三条边长是6厘米。
17.120
【分析】根据三角形三个内角的度数和是180°,等腰三角形两个底角度数相等,把一个底角看作1份,则顶角是1×4=4(份),所以三个角的度数和就是1+1+4=6(份),用180°除以总份数6,即得到每份数一个底角的度数,再乘4即得到顶角的度数。据此解答。
【解析】1+1+4=6(份)
180°÷6=30°
30°×4=120°
即一个等腰三角形的一个顶角是一个底角的4倍,这个等腰三角形的顶角是120°。
18.
9
【分析】根据题意,根据三角形三边关系,第三边必须大于两边之差且小于两边之和。已知两根小棒分别为6厘米和4厘米,第三边长度需满足:6-4<第三边<6+4,即2<第三边<10。由于长度取整厘米数,第三边最长为9厘米。以此答题即可。
【解析】根据分析可知:
6-4=2(厘米)
6+4=10(厘米)
10-1=9(厘米)
有两根长度分别为6cm、4cm的小棒,如果想再添上一根小棒(长度取整厘米数)搭成一个三角形,添上的这根小棒最长是9cm。
19.92
【分析】
已知∠2=136°,∠3和∠2组成一个平角,用180°-136°=44°,求出∠3的度数,等腰三角形两个底角度数相等,∠3=∠4,三角形内角和等于180°,用180°―44°―44°,求出∠5的度数,由图形可知∠5=∠1,据此即可求出∠1的度数。
【解析】180°-136°=44°
180°―44°―44°
=136°―44°
=92°
因此,∠1=92°。
20.66 等腰
【分析】三角形按边来分,分为不等边三角形、等腰三角形和等边三角形。有两条边相等的三角形叫作等腰三角形,等腰三角形的两个底角相等。三条边都相等的三角形叫作等边三角形,等边三角形的三个角都相等。
由题意得,一张三角形纸片的两个角分别是66°、48°,三角形的内角和为180°,那么直接用180°减去两个内角的度数即可算出第三个角的度数。然后根据三个角的大小来判断三角形的类型即可。
【解析】180°-48°-66°=66°
这个三角形中有两个角都是66°,这个三角形按边分类是等腰三角形。
如图,一张三角形纸片被撕去了一个角,这个角是66°。这个三角形按边分类是等腰三角形。
21.等腰 17
【分析】一个三角形的花坛,其中两条边刚好被两段栅栏围住,说明两条边的长度相等,两条边长都是9米,等腰三角形两条腰相等,那么这是一个等腰三角形花坛;根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,据此即可求出另外一条边的栅栏最长为米。
【解析】9+9=18(米)
第三边<18米
第三边最长是18-1=17(米)
因此,这个花坛的形状是等腰三角形,另外一条边的栅栏最长为17米。
22.50 80
【分析】三角形的内角和等于180°,等腰三角形的两底角相等,用180°减去顶角的80°等于两个底角的度数和,再除以2即等于一个底角的度数;等腰三角形的底角等于50°,用180°减去两个50°即等于顶角的度数;据此即可解答。
【解析】(180°-80°)÷2
=100°÷2
=50°
180°-50°-50°
=130°-50°
=80°
即,一个等腰三角形的顶角是80°,它的一个底角是50°;如果它的底角是50°,顶角是80°。
23.50 35
【分析】(1)三角形的内角和是180°,等腰三角形的两个底角相等,求顶角的度数,用180°减去两个底角的度数即可解答;
(2)等腰三角形的两个腰相等,测得的两条边是14分米和7分米,不知道哪条边是腰,哪条边是底边,因此需要分类讨论;
当14分米为底边时,那么7分米就是等腰三角形的腰,此时等腰三角形的三边分别为7分米、7分米、14分米,因为7+7=14,三角形的两边之和要大于第三边,所以这个等腰三角形的三边不可能是7分米、7分米、14分米;三条边的长只能是14分米、14分米、7分米,求三角形的周长,把三条边相加即可。
【解析】180°-65°-65°=50°
所以这个风筝的顶角是50°。
14+14+7=35(分米)
所以这个风筝的周长是35分米。
24.90 270
【分析】三角形的内角和为180°,四边形的内角和为360°。
原来的直角三角形中,∠1、∠2和一个直角组成一个三角形,用三角形的内角和减去90°,即可求出∠1与∠2的度数之和。
∠1、∠2、∠4、∠5组成一个四边形,用四边形的内角和减去∠1与∠2的度数之和,即是∠4与∠5的度数之和。
【解析】∠1+∠2=180°-90°=90°
∠4+∠5=360°-(∠1+∠2)=360°-90°=270°
即∠1+∠2=90°,∠4+∠5=270°。
25.直角 等腰直角/等腰
【分析】根据题意,明确三角形内角和是180°,已知三角形中有两个内角的度数和是90°,那么用180°减去90°,就可以求出第三个角的度数;三角形按角分为锐角三角形(三个角均小于90°)、直角三角形(一个角为90°)和钝角三角形(一个角大于90°)。可以判断这个三角形一定是直角三角形。在直角三角形中,已经有一个角是90°,如果还有一个内角是45°,那么第三个角的度数就是:用180°减去90°,再减去45°,可知求出第三个角的度数是45°;两个锐角相等,这个三角形有两条边相等(等腰),且有一个直角。因此,它一定是等腰直角三角形。
【解析】根据分析可知:
180°-90°=90°
180°-90°-45°=45°
如果在一个三角形中有两个内角的度数和是90°,那么这个三角形一定是直角三角形:如果在一个直角三角形中有一个内角是45°,那么这个三角形一定是等腰直角三角形。
26.
×
【分析】根据三角形三边关系,任意两边之和必须大于第三边。题目中较短的两边之和为(cm),等于最长边10cm,不满足“两边之和大于第三边”的条件,因此无法围成三角形,据此解答。
【解析】较短两边之和:(cm)
比较两边之和与最长边:10cm=10cm。
所以5cm、5cm和10cm的三根小棒无法构成三角形。
故答案为:×
27.
×
【分析】根据三角形内角和定理,三个角的和为180°。若一个三角形有两个锐角,第三个角可能是锐角、直角或钝角,因此三角形可能是锐角三角形、直角三角形或钝角三角形。
【解析】假设两个锐角均为45°,则第三个角为,此时为直角三角形;
若两个锐角均为80°,则第三个角为,此时为锐角三角形;
若两个锐角均为30°,则第三个角为,此时为钝角三角形。
因此,有两个锐角的三角形不一定是锐角三角形;
故答案为:×
28.√
【分析】锐角三角形的意义:三个角都小于90°的三角形。三角形内角和是180°;由此可知,任意两个锐角的度数和加第3个角的度数和是180°,由于第3个角是锐角,所以第3个角的度数小于90°,那么任意两个锐角的和一定大于90°,据此解答。
【解析】根据分析可知,锐角三角形任意两个锐角的和一定大于90°,原题干说法正确。
故答案为:√
29.×
【分析】三个角都是锐角的三角形叫作锐角三角形。有一个角是直角的三角形叫作直角三角形。有一个角是钝角的三角形叫作钝角三角形。三角形的内角和为180°。据此解答。
【解析】根据题意作图如下:
在锐角三角形中,60°+60°=120°。120°>60°,满足题意。在直角三角形中,60°+30°=90°。90°=90°,不满足题意。在钝角三角形中,30°+30°=60°。60°<120°,不满足题意。原题说法错误。
故答案为:×
30.×
【分析】三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。
【解析】4+5=9(厘米),9厘米=9厘米,即这三根小棒无法围成三角形。原题说法错误。
故答案为:×
31.√
【分析】根据三角形内角和可知,三角形的三个内角之和为180°。假设一个三角形中只有一个锐角,即可得出结论,据此解答。
【解析】假设一个三角形中只有一个锐角,则另外两个角都大于或等于90°,此时三个角的和必然超过180°,与三角形内角和是180°矛盾;原说法正确。
故答案为:√
32.×
【分析】根据三角形的三边关系,任意两边之和必须大于第三边。据此判断。
【解析】3+7>3,3+3<7,存在两边之和小于第三边的情况。故3米、3米和7米的三根木料不能做成一个三角形木架。原题表述错误。
故答案为:×
33.×
【分析】钝角三角形有一个角大于90°,另外两个角为锐角。根据三角形内角和为180°,钝角的度数大于90°,因此另外两个锐角的和必然小于90°。据此判断。
【解析】例如,若钝角为100°,则两锐角和为80°;若钝角为120°,则两锐角和为60°,均小于90°。
因此钝角三角形的两个锐角的和小于90°。题干说法错误。
故答案为:×
34.78°;60°
【分析】根据三角形内角和是180°和图中给出的度数,用180°减去三角形的两个已知角度,可以求得未知角的度数。
【解析】根据分析可知:
180°-(65°+37°)
=180°-102°
= 78°
图一的未知角的度数是 78°。
180°-(90°+30°)
=180°-120°
= 60°
图二的未知角的度数是 60°。
35.见详解
【分析】从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高,这个顶点所对的边叫做三角形的底。据此作图。
【解析】
36.底12厘米;腰15厘米
【分析】等腰三角形的两腰相等,两条腰长加上底的长度就是它的周长。根据周长是42厘米,腰比底长3厘米。画出线段图即可。
用它的周长减去2个3厘米的长度就是3个底的长度。算出结果除以3就是一条底的长度。再用底的长度加上3厘米就是腰的长度。
【解析】根据条件,画出的线段图如下所示:
底长:
(42-2×3)÷3
=(42-6)÷3
=36÷3
=12(厘米)
腰长:12+3=15(厘米)
答:它的底是12厘米和腰是15厘米。
37.不同意;理由见详解
【分析】求多边形的内角和,可以看这个多边形可以分成几个三角形,三角形的内角和为180°,直接用180°乘可以分成三角形的个数即可算出多边形的内角和。由题意得,小瓯把六边形变成6个三角形。这样分割时把中间的周角也分给了6个三角形,这个周角原本不是六边形的内角,所以最后算出来的结果会比正确的结果多一个周角的度数。
【解析】答:不同意小瓯的方法。因为这样分割把中间6个角的度数和也算进去了,也就是多算了一个周角的度数,正确的度数应该等于1080°减去360°。
38.24厘米
【分析】根据题意,长方形的周长=(长+宽)×2,已知用一根铁丝刚好围成一个长25cm,宽15cm的长方形,先求出铁丝的长度;又知等腰三角形的两腰相等,用铁丝的长度减去两个28,就是这个等腰三角形的底的长度;列式计算即可。
【解析】根据分析可知:
(25+15)×2
=40×2
=80(厘米)
80-28-28
=52-28
=24(厘米)
答:这个等腰三角形的底是24厘米。
39.5厘米,3厘米和4厘米;5厘米,5厘米和2厘米;4厘米,4厘米和4厘米
【分析】三角形两边之和大于第三边,两边之差小于第三边;三角形中三边和等于12厘米, 据此写出所以情况即可解题。
【解析】12=5+3+4;5+3=8(厘米);8厘米>4厘米;
12=5+2+5;5+2=7(厘米);7厘米>5厘米;
12=4+4+4;4+4=8(厘米);8厘米>4厘米;
答:可以剪成三角形的边长分别是5厘米,3厘米和4厘米;5厘米,5厘米和2厘米;4厘米,4厘米和4厘米。
40.60厘米;600平方厘米
【分析】仔细观察发现展开后纸与桌面形成一些等边三角形。等边三角形三条边长都相等,测量展开后的长度是30厘米,那么这张纸原本的长度是30×2=60(厘米),长方形的面积=长×宽,据此计算。
【解析】30×2=60(厘米)
60×10=600(平方厘米)
答:这张长方形纸的长是60厘米,面积是600平方厘米。
41.7个;见解析
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。14÷2=71,截出的三条线段的最大边最大是7厘米,最小是5厘米,由此进行推理归纳即可得出结论。
【解析】根据分析可知:
最大边为7厘米时,另两边之和为8厘米。
1+7=8(厘米)三边分别为:7厘米、7厘米、1厘米
2+6=8(厘米)三边分别为:7厘米、2厘米、6厘米
3+5=8(厘米)三边分别为:7厘米、3厘米、5厘米
4+4=8(厘米)三边分别为:7厘米、4厘米、4厘米
可构成4个不同的三角形。
最大边为6厘米时,另两边之和为9厘米。
3+6=9(厘米) 三边分别为:6厘米、3厘米、6厘米
4+5=9(厘米)三边分别为:6厘米、4厘米、5厘米
可构成2个不同的三角形。
最大边为5厘米时,另两边之和为10厘米。
5+5=10(厘米)三边分别为:5厘米、5厘米、5厘米
可构成1个不同的三角形。
4+2+1=7(个)
答:用这三条线段可以组成7个不同的三角形。
42.沿MN走最近;一样长;见详解
【分析】等边三角形的三条边长度相等。由题意得,从M到N,沿着MN走是最近的,因为两点之间线段是最短的;第二问,可以根据等边三角形的特征判断出各个线段长度之间的关系。
【解析】沿MN走最近,MN=80米。因为三个三角形都是大小不同的等边三角形,所以MD=ND=MO+ON,MO=MA=OA,OB=ON=BN。所以MD+DN=MN×2=(50+30)×2=80×2=160(米),MA+AO+OB+BN=MO×2+ON×2=50×2+30×2=100+60=160(米)。160=160,所以其它两条路一样长。
答:沿MN走最近且其它两条路一样长。
43.不对;理由见详解
【分析】根据题意,连接O、A、B这三点围成一个三角形,三角形任意两边的和大于第三条边。据此解答即可。
【解析】李叔叔说得不对。因为三角形任意两边的和大于第三边,所以OA+OB的长度应该大于AB的长度,15+10=25(米),A、B之间的距离应该比25米小,不可能是25米。
44.见详解
【分析】有两条边相等的三角形叫作等腰三角形。三角形三边的关系:任意两边之和大于第三边,任意两边之差小于第三边。由题意得,淘气要把一根20厘米长的吸管剪成3段(每段长是整厘米数),再用这三段吸管围成一个等腰三角形,那么这三段应该有两段的长度应该相等且满足构成三角形的条件。据此解答。
【解析】6+6+8=12+8=20(厘米),6=6,6+6=12>8,即淘气可以将吸管剪成6厘米,6厘米,8厘米的小段。
7+7+6=14+6=20(厘米),7=7,6+7=13>7,即淘气可以将吸管剪成7厘米,7厘米,6厘米的小段。
8+8+4=16+4=20(厘米),8=8,8+4=12>8,即淘气可以将吸管剪成8厘米,8厘米,4厘米的小段。
答:淘气可以将吸管剪成6厘米,6厘米,8厘米的小段,也可以将吸管剪成7厘米,7厘米,6厘米的小段,还可以将吸管剪成8厘米,8厘米,4厘米的小段。(答案不唯一)
45.(1)有两种围法;见详解
(2)25厘米
【分析】(1)已知这个等腰三角形框架的两条边分别是7厘米和11厘米,根据等腰三角形有两条相等的边和一条底边,我们需要考虑两种情况:①两条相等的边为7厘米,底边为11厘米。②两条相等的边为11厘米,底边为7厘米。再根据三角形的三边关系:三角形三边之和大于第三边,进行判断即可。
(2)把三角形的三条边相加,分别求出两种围法三角形的周长,然后取较小的值即可。
【解析】(1)两种情况:
①两条相等的边为7厘米,底边为11厘米。
7+7=14(厘米);14厘米>11厘米
7+11=18(厘米);18厘米>7厘米
因此两条相等的边为7厘米,底边为11厘米可以围成一个三角形。
②两条相等的边为11厘米,底边为7厘米。
11+11=22(厘米),22厘米>7厘米
7+11=18(厘米);18厘米>11厘米
因此两条相等的边为7厘米,底边为11厘米可以围成一个三角形。
综上可知,有两种围法。
画图如下:
(2)11+11+7=29(厘米)
7+7+11=25(厘米)
25<29
答:至少需要25厘米长的铁丝。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
