北师大版2019必修第一册2.1 生活中的变量关系 课件(共17张PPT)
文档属性
| 名称 | 北师大版2019必修第一册2.1 生活中的变量关系 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 09:57:53 | ||
图片预览




文档简介
(共17张PPT)
1 生活中的变量关系
北师大版(2019)高中数学必修第一册
第二章 函数
第1节 生活中的变量关系
导入课题
新知讲授
典例剖析
课堂小结
储油量与油面高度存在着依赖关系,也与油面宽度
存在着依赖关系.
对于油面高度的每一个取值,都有唯一的储油量和
它对应.
但是,每一个油面宽度的值,却对应着两个储油量.
像上面这样的变量关系,在实际生活中还有很多,摸清变量之间有何关系,能帮助我们解决很多
生活中的问题,因此,今天我们要更加深入地学习生活中的变量关系.
例1 如图,是某高速公路加油站的图片,加油站在地下常用
圆柱体储油罐储存汽油等燃料.储油罐的长度、截面半径、是常
量,油面高度、油面宽度、储油量是变量.
一、依赖关系
导入课题
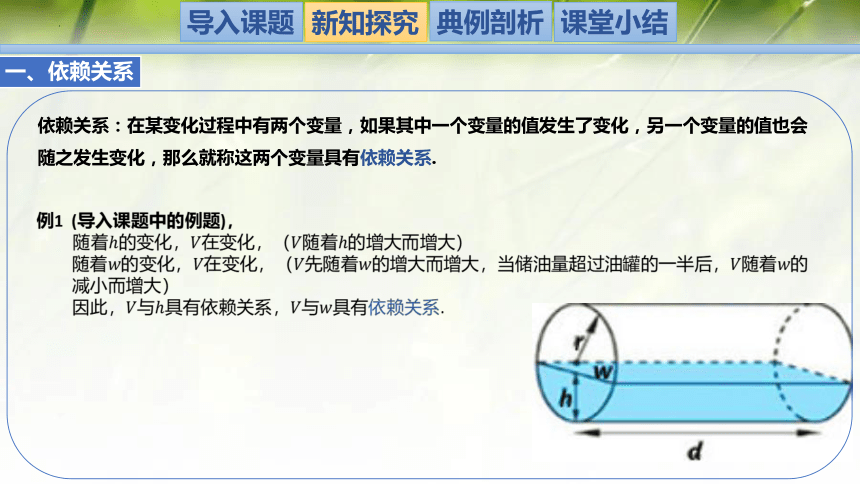
依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会
随之发生变化,那么就称这两个变量具有依赖关系.
新知探究
典例剖析
课堂小结
例1 (导入课题中的例题),
随着的变化,在变化,(随着的增大而增大)
随着的变化,在变化,(先随着的增大而增大,当储油量超过油罐的一半后,随着的
减小而增大)
因此,与具有依赖关系,与具有依赖关系.
一、依赖关系
导入课题
新知探究
典例剖析
课堂小结
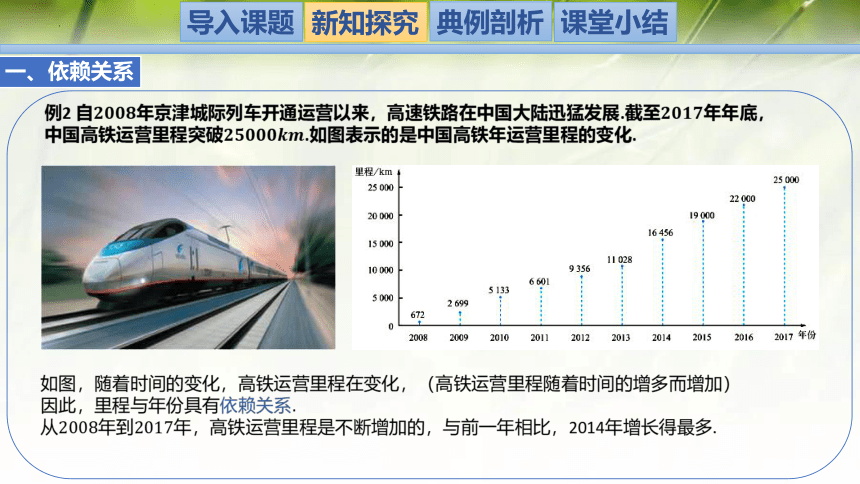
例2 自年京津城际列车开通运营以来,高速铁路在中国大陆迅猛发展.截至年年底,
中国高铁运营里程突破.如图表示的是中国高铁年运营里程的变化.
如图,随着时间的变化,高铁运营里程在变化,(高铁运营里程随着时间的增多而增加)
因此,里程与年份具有依赖关系.
从年到年,高铁运营里程是不断增加的,与前一年相比,2014年增长得最多.
二、函数关系
导入课题
新知探究
典例剖析
课堂小结
初中的函数概念:有两个变量和,对于变量的每一个值,变量都有唯一确定的值和它对应,那
么就是的函数,其中是自变量,是因变量,表示两个变量关系的函数的代数式,叫函数解析式.
函数关系:若是的函数,我们称变量与变量具有函数关系.
注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的
值和它对应”.
函数名字的由来:在中国,函数一词是清代数学家李善兰(1811-1882)最初使用的。他在1859年与
英国学者烈亚力(1815-1887)合译的《代数学》一书中,将“function”译作“函数”。老先生为什
么给它取这么个名字呢?
函:即信也!老先生巧妙的用寄信来比喻函数,就是为了方便后来学习的人能够轻易理解函数的意义。
那我们拿寄信来理解函数,就比较方便了!
顺着这个比喻往下理解,就很容易理解“使对于集合中的任意一个x,在集合中都有唯一一个确定的数
y和它对应”这句话了,就是说信只能有一个收信人,不可能一封信有多个收信地址的(清朝那时候
没有群发功能);而一个收信人却可以收到很多信,即一个只能对应一个,而一个却能有多个与
之相对应.
二、函数关系
导入课题
新知探究
典例剖析
课堂小结
初中的函数概念:有两个变量和,对于变量的每一个值,变量都有唯一确定的值和它对应,那
么就是的函数,其中是自变量,是因变量,表示两个变量关系的函数的代数式,叫函数解析式.
函数关系:若是的函数,我们称变量与变量具有函数关系.
注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的
值和它对应”.
例1中,是的函数,即与具有函数关系, 不是的函数,即与没有函数关系.
对于变量的每一个值,变量都有唯一确定的值与它对应.
对于变量的每一个值,变量有不止一个值与它对应(一个对应两个).
例2中,高铁运营里程是时间的函数,即高铁运营里程与时间具有函数关系.
对于变量时间的每一个值,变量高铁运营里程都有唯一确定的值与它对应.
例如: 1,一定量的水银,温度与其体积间存在函数关系,温度越高,体积越大.
2,银行给定本金和利率后,活期存款的利息依存款的天数而定,利息是天数的函数,天数越多,
利息越多.
3,田径比赛时,铅球运动员的掷远距离和出手速度、出手角度、出手高度均有关系,当出手速
度和出手高度确定后,调整好出手速度,会使铅球掷得更远一些,这时,运动员的掷远距离是出
手角度的函数.
二、函数关系
导入课题
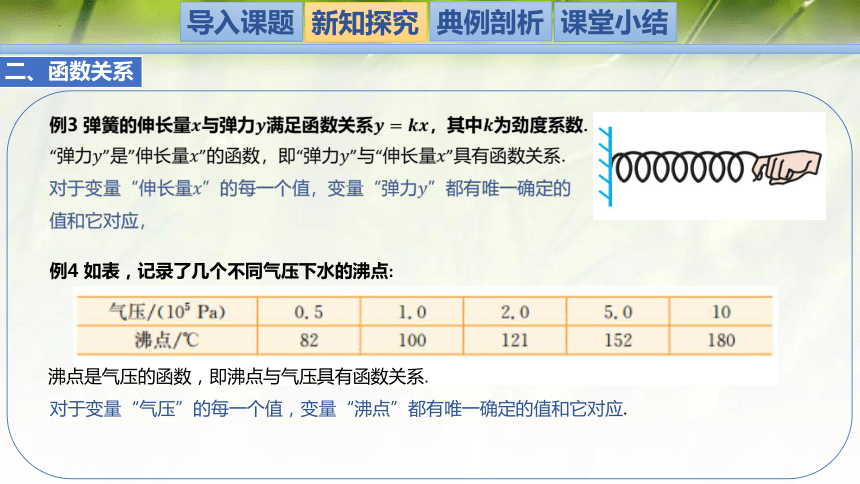
例3 弹簧的伸长量与弹力满足函数关系,其中为劲度系数.
新知探究
典例剖析
课堂小结
“弹力”是”伸长量”的函数,即“弹力”与“伸长量”具有函数关系.
对于变量“伸长量”的每一个值,变量“弹力”都有唯一确定的
值和它对应,
例4 如表,记录了几个不同气压下水的沸点:
沸点是气压的函数,即沸点与气压具有函数关系.
对于变量“气压”的每一个值,变量“沸点”都有唯一确定的值和它对应.
三、依赖关系与函数关系的区别
导入课题
新知探究
典例剖析
课堂小结
例1中,是的函数,即与具有函数关系.
不是的函数,即与没有函数关系,但具有依赖关系.
例2中,高铁运营里程是时间的函数,即高铁运营里程与时间具有函数关系.
例3中,弹力”是”伸长量”的函数,即“弹力”与“伸长量”具有函数关系.
例4中,沸点是气压的函数,即沸点与气压具有函数关系.
1、函数关系一定是依赖关系,而依赖关系不一定是函数关系.
2、要确定两变量是否有函数关系,需先分清谁是自变量,谁是因变量,当两个变量之间具有函数关系时,就不用再说它们之间还有依赖关系了.
函数关系
依赖关系
四、分段函数
导入课题
分段函数:在自变量的不同取值范围内,因变量与自变量有不同的函数关系,需要用不同的解析
式来表示的函数叫作分段函数.
新知探究
典例剖析
课堂小结
例如:某市空调公共汽车的票价按下列规则制定:
①以内(含),票价2元.
②以上,每增加,票价增加1元(不足的按计算).
已知两个相邻的公共汽车站间相距,沿途(包括起点站和终点站)有11个汽车站.
请列出从起点站出发,公共汽车的行程()与票价(元)间的函数解析式.
,形容这样的函数解析式,就叫作分段函数.
导入课题
新知探究
典例剖析
课堂小结
例5 绿化可以改变小环境气候.某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,如图,是这两个观测点某一天的气温曲线图.为了方便比较,将两条曲线画在了同一平面直角坐标系中,如图所示,请问气温与时间具有函数关系吗?
解:
图中的两条曲线反映的都是对于“时间”
的每一个值,都有唯一确定的“气温”
值和它对应,所以每一条曲线都表示了
一个函数关系,即气温是时间的函数,
即气温与时间具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
例6 某地电力公司为鼓励市民节约用电,采取阶梯电价,即按月用电量分段计费办法,居民每月应缴电费(单位:元)与用电量(单位:)的关系是
请问变量与变量具有函数关系吗?
解:
对于变量“用电量()”的每一个值,
变量”应缴电费()”都有唯一确定的值与之对应,所以应缴电费是用电量的函数,即应缴电费与用电量具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习1:某电器商店以2500元/台的价格购进了一批电视机,然后以2900元/台的价格售出,随着售出
台数的变化,商店的利润是怎样变化的?利润和售出的台数之间存在函数关系吗?
解:设商店的售出台数为,利润为,依题意得,,
所以随着的增大而增大,
且对于售出台数的每一个值,都有唯一确定的利润的值与之对应,
所以利润是售出台数的函数,
所以利润和售出台数之间具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习2:坐电梯时,电梯距地面的高度与时间之间存在怎样的依赖关系?
解:当电梯上升时,电梯距地面的高度随时间的增加而增加,
当电梯下降时,电梯距地面的高度随时间的增加而减少,
所以电梯距地面的高度与时间之间存在依赖关系.
当电梯上升和下降到同一楼层时,经历的时间是不一样的,电梯距地面的高度却一样,
所以对于时间的每一个值,不止一个确定的电梯距地面的高度与之对应,
所以时间不是电梯距地面的高度的函数,
但对于时间的每一个值,有唯一一个确定的电梯距地面的高度与之对应,
所以电梯距地面的高度是时间的函数,即电梯距地面的高度与时间之间存在函数关系,
所以利电梯距地面的高度与时间存在函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习3:在一定量的水中加入蔗糖,糖水的质量分数与所加蔗糖的质量之间存在怎样的依赖关系?
解:设所加蔗糖的质量为,糖水的质量分数为为,一定量的水的质量为,依题意得,
,所以随着的增大而增大,
且对于所加蔗糖质量的每一个值,都有唯一确定的糖水质量分数的值与之对应,
所以糖水的质量分数是所加蔗糖质量的函数,
所以糖水的质量分数和所加蔗糖质量具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
本节重点
思想方法
1,利用函数解析式解决实际问题的思想是高中数学中比较重要的一种思想,要逐步掌握建立数学模型解决实际问题的能力.
一、依赖关系
二、函数关系
三、依赖关系与函数关系的区别
四、分段函数
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:课本P51 A组T1
作业2:课本P51 B组T1
谢谢聆听!
1 生活中的变量关系
北师大版(2019)高中数学必修第一册
第二章 函数
第1节 生活中的变量关系
导入课题
新知讲授
典例剖析
课堂小结
储油量与油面高度存在着依赖关系,也与油面宽度
存在着依赖关系.
对于油面高度的每一个取值,都有唯一的储油量和
它对应.
但是,每一个油面宽度的值,却对应着两个储油量.
像上面这样的变量关系,在实际生活中还有很多,摸清变量之间有何关系,能帮助我们解决很多
生活中的问题,因此,今天我们要更加深入地学习生活中的变量关系.
例1 如图,是某高速公路加油站的图片,加油站在地下常用
圆柱体储油罐储存汽油等燃料.储油罐的长度、截面半径、是常
量,油面高度、油面宽度、储油量是变量.
一、依赖关系
导入课题
依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会
随之发生变化,那么就称这两个变量具有依赖关系.
新知探究
典例剖析
课堂小结
例1 (导入课题中的例题),
随着的变化,在变化,(随着的增大而增大)
随着的变化,在变化,(先随着的增大而增大,当储油量超过油罐的一半后,随着的
减小而增大)
因此,与具有依赖关系,与具有依赖关系.
一、依赖关系
导入课题
新知探究
典例剖析
课堂小结
例2 自年京津城际列车开通运营以来,高速铁路在中国大陆迅猛发展.截至年年底,
中国高铁运营里程突破.如图表示的是中国高铁年运营里程的变化.
如图,随着时间的变化,高铁运营里程在变化,(高铁运营里程随着时间的增多而增加)
因此,里程与年份具有依赖关系.
从年到年,高铁运营里程是不断增加的,与前一年相比,2014年增长得最多.
二、函数关系
导入课题
新知探究
典例剖析
课堂小结
初中的函数概念:有两个变量和,对于变量的每一个值,变量都有唯一确定的值和它对应,那
么就是的函数,其中是自变量,是因变量,表示两个变量关系的函数的代数式,叫函数解析式.
函数关系:若是的函数,我们称变量与变量具有函数关系.
注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的
值和它对应”.
函数名字的由来:在中国,函数一词是清代数学家李善兰(1811-1882)最初使用的。他在1859年与
英国学者烈亚力(1815-1887)合译的《代数学》一书中,将“function”译作“函数”。老先生为什
么给它取这么个名字呢?
函:即信也!老先生巧妙的用寄信来比喻函数,就是为了方便后来学习的人能够轻易理解函数的意义。
那我们拿寄信来理解函数,就比较方便了!
顺着这个比喻往下理解,就很容易理解“使对于集合中的任意一个x,在集合中都有唯一一个确定的数
y和它对应”这句话了,就是说信只能有一个收信人,不可能一封信有多个收信地址的(清朝那时候
没有群发功能);而一个收信人却可以收到很多信,即一个只能对应一个,而一个却能有多个与
之相对应.
二、函数关系
导入课题
新知探究
典例剖析
课堂小结
初中的函数概念:有两个变量和,对于变量的每一个值,变量都有唯一确定的值和它对应,那
么就是的函数,其中是自变量,是因变量,表示两个变量关系的函数的代数式,叫函数解析式.
函数关系:若是的函数,我们称变量与变量具有函数关系.
注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的
值和它对应”.
例1中,是的函数,即与具有函数关系, 不是的函数,即与没有函数关系.
对于变量的每一个值,变量都有唯一确定的值与它对应.
对于变量的每一个值,变量有不止一个值与它对应(一个对应两个).
例2中,高铁运营里程是时间的函数,即高铁运营里程与时间具有函数关系.
对于变量时间的每一个值,变量高铁运营里程都有唯一确定的值与它对应.
例如: 1,一定量的水银,温度与其体积间存在函数关系,温度越高,体积越大.
2,银行给定本金和利率后,活期存款的利息依存款的天数而定,利息是天数的函数,天数越多,
利息越多.
3,田径比赛时,铅球运动员的掷远距离和出手速度、出手角度、出手高度均有关系,当出手速
度和出手高度确定后,调整好出手速度,会使铅球掷得更远一些,这时,运动员的掷远距离是出
手角度的函数.
二、函数关系
导入课题
例3 弹簧的伸长量与弹力满足函数关系,其中为劲度系数.
新知探究
典例剖析
课堂小结
“弹力”是”伸长量”的函数,即“弹力”与“伸长量”具有函数关系.
对于变量“伸长量”的每一个值,变量“弹力”都有唯一确定的
值和它对应,
例4 如表,记录了几个不同气压下水的沸点:
沸点是气压的函数,即沸点与气压具有函数关系.
对于变量“气压”的每一个值,变量“沸点”都有唯一确定的值和它对应.
三、依赖关系与函数关系的区别
导入课题
新知探究
典例剖析
课堂小结
例1中,是的函数,即与具有函数关系.
不是的函数,即与没有函数关系,但具有依赖关系.
例2中,高铁运营里程是时间的函数,即高铁运营里程与时间具有函数关系.
例3中,弹力”是”伸长量”的函数,即“弹力”与“伸长量”具有函数关系.
例4中,沸点是气压的函数,即沸点与气压具有函数关系.
1、函数关系一定是依赖关系,而依赖关系不一定是函数关系.
2、要确定两变量是否有函数关系,需先分清谁是自变量,谁是因变量,当两个变量之间具有函数关系时,就不用再说它们之间还有依赖关系了.
函数关系
依赖关系
四、分段函数
导入课题
分段函数:在自变量的不同取值范围内,因变量与自变量有不同的函数关系,需要用不同的解析
式来表示的函数叫作分段函数.
新知探究
典例剖析
课堂小结
例如:某市空调公共汽车的票价按下列规则制定:
①以内(含),票价2元.
②以上,每增加,票价增加1元(不足的按计算).
已知两个相邻的公共汽车站间相距,沿途(包括起点站和终点站)有11个汽车站.
请列出从起点站出发,公共汽车的行程()与票价(元)间的函数解析式.
,形容这样的函数解析式,就叫作分段函数.
导入课题
新知探究
典例剖析
课堂小结
例5 绿化可以改变小环境气候.某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,如图,是这两个观测点某一天的气温曲线图.为了方便比较,将两条曲线画在了同一平面直角坐标系中,如图所示,请问气温与时间具有函数关系吗?
解:
图中的两条曲线反映的都是对于“时间”
的每一个值,都有唯一确定的“气温”
值和它对应,所以每一条曲线都表示了
一个函数关系,即气温是时间的函数,
即气温与时间具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
例6 某地电力公司为鼓励市民节约用电,采取阶梯电价,即按月用电量分段计费办法,居民每月应缴电费(单位:元)与用电量(单位:)的关系是
请问变量与变量具有函数关系吗?
解:
对于变量“用电量()”的每一个值,
变量”应缴电费()”都有唯一确定的值与之对应,所以应缴电费是用电量的函数,即应缴电费与用电量具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习1:某电器商店以2500元/台的价格购进了一批电视机,然后以2900元/台的价格售出,随着售出
台数的变化,商店的利润是怎样变化的?利润和售出的台数之间存在函数关系吗?
解:设商店的售出台数为,利润为,依题意得,,
所以随着的增大而增大,
且对于售出台数的每一个值,都有唯一确定的利润的值与之对应,
所以利润是售出台数的函数,
所以利润和售出台数之间具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习2:坐电梯时,电梯距地面的高度与时间之间存在怎样的依赖关系?
解:当电梯上升时,电梯距地面的高度随时间的增加而增加,
当电梯下降时,电梯距地面的高度随时间的增加而减少,
所以电梯距地面的高度与时间之间存在依赖关系.
当电梯上升和下降到同一楼层时,经历的时间是不一样的,电梯距地面的高度却一样,
所以对于时间的每一个值,不止一个确定的电梯距地面的高度与之对应,
所以时间不是电梯距地面的高度的函数,
但对于时间的每一个值,有唯一一个确定的电梯距地面的高度与之对应,
所以电梯距地面的高度是时间的函数,即电梯距地面的高度与时间之间存在函数关系,
所以利电梯距地面的高度与时间存在函数关系.
导入课题
新知探究
典例剖析
课堂小结
练习3:在一定量的水中加入蔗糖,糖水的质量分数与所加蔗糖的质量之间存在怎样的依赖关系?
解:设所加蔗糖的质量为,糖水的质量分数为为,一定量的水的质量为,依题意得,
,所以随着的增大而增大,
且对于所加蔗糖质量的每一个值,都有唯一确定的糖水质量分数的值与之对应,
所以糖水的质量分数是所加蔗糖质量的函数,
所以糖水的质量分数和所加蔗糖质量具有函数关系.
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
本节重点
思想方法
1,利用函数解析式解决实际问题的思想是高中数学中比较重要的一种思想,要逐步掌握建立数学模型解决实际问题的能力.
一、依赖关系
二、函数关系
三、依赖关系与函数关系的区别
四、分段函数
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:课本P51 A组T1
作业2:课本P51 B组T1
谢谢聆听!
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
