2025年安徽省安庆市迎江区部分学校六月联考三模数学试卷(含答案)
文档属性
| 名称 | 2025年安徽省安庆市迎江区部分学校六月联考三模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 22:38:46 | ||
图片预览




文档简介
2025年安徽省安庆市迎江区部分学校六月联考三模数学试卷
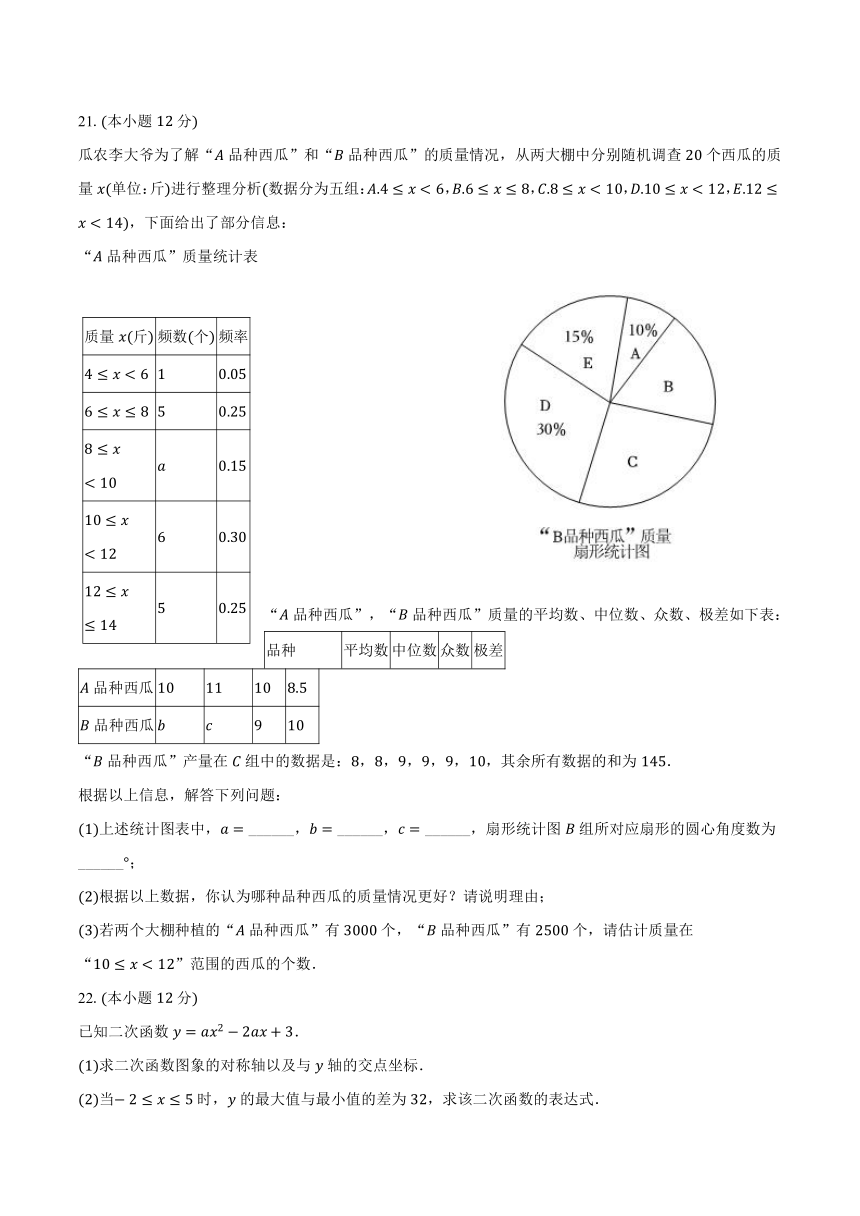
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中是正整数的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功如图是一块雕刻印章的材料,其俯视图为( )
A.
B.
C.
D.
4.用配方法解一元二次方程,此方程可化为( )
A. B. C. D.
5.如图,在中,平分,若,,则的长为( )
A.
B.
C.
D.
6.如图,在中,弦,相交于点若,,则的度数为( )
A.
B.
C.
D.
7.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B. C. D.
8.半径为的圆中,的圆心角所对的弧长为( )
A. B. C. D.
9.已知实数,,满足,,则下列结论正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.如图,为等边三角形,,的平分线交于点,为上一动点,连接,以为边在右侧作等边,连接,则周长的最小值( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
11.不等式的解集为______.
12.已知关于的方程的解是负数,则的取值范围是______.
13.如图,矩形,点在的延长线上,连接交的平分线于点,其中,,,则的长为______.
14.平面直角坐标系中,是坐标原点,点,在抛物线的图象上,连接,,轴.
______;
若将抛物线向下平移个单位,使平移后得到的抛物线顶点落在的内部不包括的边界则的取值范围是______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别为,,
将绕着点按顺时针方向旋转得到,请画出;
将关于轴对称,得到,请画出,并直接写出点的坐标.
17.本小题分
近年来安徽宿州市、涡阳县、蒙城县等许多地方大力推进“客货邮”融合发展模式助力乡村振兴,这种模式不仅提升了工业品下乡和农产品出村的效率,还推动了农村电商和物流配送的发展涡阳县克拉香草种植基地计划将的迷迭香、百里香等香草货物通过“客货邮”融合专车一次性运往县城的物流中心,现有甲、乙两种型号的专车,其载重量和运费如表所示:
专车 甲 乙
载重量吨辆
运费元辆
如果甲、乙两种专车的运输总费用恰好为元,则安排了甲专车多少辆?
18.本小题分
如图,将形状、大小完全相同的“”和线段按照一定的规律摆成下列图形,第个图案中“”的个数为,第个图案中“”的个数为,第个图案中“”的个数为,,以此类推.
第个图案中“”的个数是______.
请用含的代数式表示第个图案中“”的个数.
请用含的代数式表示第个图案中最长的线段上“”的个数.
19.本小题分
如图一是屏幕投影仪投屏情景图,图二是其侧面抽象示意图,,,是支架的一部分,投影光线与投影仪近似在同一直线上,已知与地面垂直,且的长为,的长为,距墙面的水平距离为,若投影光线与的夹角,与地面的夹角,求光源投屏最高点到地面的距离结果精确到,参考数据:,,,
20.本小题分
如图,在中,、为弦,为直径,于,于,与相交于.
求证:;
若,,求的半径.
21.本小题分
瓜农李大爷为了解“品种西瓜”和“品种西瓜”的质量情况,从两大棚中分别随机调查个西瓜的质量单位:斤进行整理分析数据分为五组:,,,,,下面给出了部分信息:
“品种西瓜”质量统计表
质量斤 频数个 频率
“品种西瓜”,“品种西瓜”质量的平均数、中位数、众数、极差如下表:
品种 平均数 中位数 众数 极差
品种西瓜
品种西瓜
“品种西瓜”产量在组中的数据是:,,,,,,其余所有数据的和为.
根据以上信息,解答下列问题:
上述统计图表中, ______, ______, ______,扇形统计图组所对应扇形的圆心角度数为______;
根据以上数据,你认为哪种品种西瓜的质量情况更好?请说明理由;
若两个大棚种植的“品种西瓜”有个,“品种西瓜”有个,请估计质量在“”范围的西瓜的个数.
22.本小题分
已知二次函数.
求二次函数图象的对称轴以及与轴的交点坐标.
当时,的最大值与最小值的差为,求该二次函数的表达式.
若,直线经过抛物线的顶点,并与该抛物线的另一交点为点,当取最小值时,求的值.
23.本小题分
如图,在边长为的正方形中,,分别是边,上的点,连接,,.
若是的中点.
如图,当时,求证:.
如图,当时,求的值.
如图,延长,交于点,当,时,求证:.
2025年安徽省安庆市迎江区部分学校六月联考三模数学试卷答案和解析
一、选择题:本题共10小题,每小题4分,共40分。
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
二、填空题:本题共4小题,每小题5分,共20分。
11.
12.
13.
【解析】解:如图,取的中点,连接交于点,
,,,
,,,
,是等腰直角三角形,
四边形是矩形,
,,
,
,
∽,
,
,
,
由题意可得:,
,
∽,
,
.
故答案为:.
14.;
.
【解析】解:点,在抛物线的图象上,
,
,
二次函数的解析式为:,
故答案为:;
由知抛物线的解析式为,
抛物线向下平移个单位的解析式为,
顶点坐标为,
设直线的解析式为,
代入点,得到,
,
直线的解析式为,
时,,
使平移后抛物线顶点落在的内部不包括的边界,
,
.
故答案为:.
三、解答题:本题共9小题,共90分。
15.(8分)解:
.
16.(8分)解:如图,即为所求;
如图,即为所求,点的坐标.
17.(8分)安排了甲专车辆.
【解析】解:设安排了甲专车辆.
.
解得:.
答:安排了甲专车辆.
18.(8分);
;
.
【解析】解:由所给图形可知,
第个图案中“”的个数为:;
第个图案中“”的个数为:;
第个图案中“”的个数为:;
,
所以第个图案中“”的个数为个.
当时,
个,
即第个图案中“”的个数为个.
故答案为:.
由知,
第个图案中“”的个数为个.
由所给图形可知,
第个图案中最长的线段上“”的个数为,
第个图案中最长的线段上“”的个数为,
第个图案中最长的线段上“”的个数为,
,
所以第个图案中最长的线段上“”的个数为个.
19.(10分)解:延长交于点,过点作,垂足为,
由题意得:,,,,
,
,
在中,,,
,
,
,
在中,,
,
光源投屏最高点到地面的距离约为.
20.(10分)证明:如图,连接,
于,于,
又,
,
,
,
,
,
,
,
,
又,
;
解:如图,连接,设,则,
,
,
于,,
,
在中,,
即,
解得或舍.
即的半径为.
21.(12分),,,;
品种西瓜的质量情况更好,见解析;
大约有个.
【解析】解:由题意得,,
,
“品种西瓜”共个,根据扇形统计图可知:、共个,中位数是第、个,即在组最后个,即为:
;
组圆心角度数为:.
故答案为:,,,;
品种西瓜的质量情况更好,理由如下:
因为样本中“品种西瓜”的平均数、中位数、众数均高于“品种西瓜”,所以“品种西瓜”的质量情况更好;
个,
答:大约有个.
22.(12分)对称轴是直线,交点坐标为;
或;
.
【解析】解:已知二次函数,
二次函数图象的对称轴是直线.
当时,得,
二次函数图象与轴的交点坐标为;
若,抛物线开口向上,对称轴为直线,
,
当时,二次函数有最小值,
当时,二次函数有最大值,
,
解得,
该二次函数的表达式为.
若,抛物线开口向下,对称轴为直线,
当时,的最大值与最小值的差为,
当时,二次函数有最大值,
当时,二次函数有最小值,
,
解得,
该二次函数的表达式为,
综上所述,该二次函数的表达式为或;
由可得,二次函数图象的顶点坐标为.
直线经过抛物线的顶点,并与该抛物线的另一交点为点,
,
解得:,
.
联立得:,
解得或,
点.
设,则点,
,
,
,
当时,取最小值,
,即.
23.(14分)见解析;
;
见解析.
【解析】证明:四边形是正方形,
,.
是的中点,,
,
∽,
.
,
,
,
.
解:如图,延长交的延长线于点,过点作交的延长线于点.
,,
∽,
.
,,
.
设,.
在中,由勾股定理得:,
,
,
,
,
解得,
,,
在中,由勾股定理得:,
,
,
.
,
,
.
证明:如图,过点作,交的延长线于点.
设,,,
在中,由勾股定理得:,
.
,,
∽,
,
,
,.
在中,,
,
,
整理得,
解得:,
,
.
,
∽,
,
,
,
.
由由题意可得,证得∽,利用直角三角形的两个锐角互余即可得,可得结论;
延长交的延长线于点,过点作交的延长线于点证得∽,得,推得,设,,得,解得,可得,利用得,即可得;
过点作,交的延长线于点设,,,证得∽,即得,推得、,通过得,整理得一元二次方程,解得,再通过平行线分线段成比例得即可求解.
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中是正整数的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功如图是一块雕刻印章的材料,其俯视图为( )
A.
B.
C.
D.
4.用配方法解一元二次方程,此方程可化为( )
A. B. C. D.
5.如图,在中,平分,若,,则的长为( )
A.
B.
C.
D.
6.如图,在中,弦,相交于点若,,则的度数为( )
A.
B.
C.
D.
7.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B. C. D.
8.半径为的圆中,的圆心角所对的弧长为( )
A. B. C. D.
9.已知实数,,满足,,则下列结论正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.如图,为等边三角形,,的平分线交于点,为上一动点,连接,以为边在右侧作等边,连接,则周长的最小值( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
11.不等式的解集为______.
12.已知关于的方程的解是负数,则的取值范围是______.
13.如图,矩形,点在的延长线上,连接交的平分线于点,其中,,,则的长为______.
14.平面直角坐标系中,是坐标原点,点,在抛物线的图象上,连接,,轴.
______;
若将抛物线向下平移个单位,使平移后得到的抛物线顶点落在的内部不包括的边界则的取值范围是______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别为,,
将绕着点按顺时针方向旋转得到,请画出;
将关于轴对称,得到,请画出,并直接写出点的坐标.
17.本小题分
近年来安徽宿州市、涡阳县、蒙城县等许多地方大力推进“客货邮”融合发展模式助力乡村振兴,这种模式不仅提升了工业品下乡和农产品出村的效率,还推动了农村电商和物流配送的发展涡阳县克拉香草种植基地计划将的迷迭香、百里香等香草货物通过“客货邮”融合专车一次性运往县城的物流中心,现有甲、乙两种型号的专车,其载重量和运费如表所示:
专车 甲 乙
载重量吨辆
运费元辆
如果甲、乙两种专车的运输总费用恰好为元,则安排了甲专车多少辆?
18.本小题分
如图,将形状、大小完全相同的“”和线段按照一定的规律摆成下列图形,第个图案中“”的个数为,第个图案中“”的个数为,第个图案中“”的个数为,,以此类推.
第个图案中“”的个数是______.
请用含的代数式表示第个图案中“”的个数.
请用含的代数式表示第个图案中最长的线段上“”的个数.
19.本小题分
如图一是屏幕投影仪投屏情景图,图二是其侧面抽象示意图,,,是支架的一部分,投影光线与投影仪近似在同一直线上,已知与地面垂直,且的长为,的长为,距墙面的水平距离为,若投影光线与的夹角,与地面的夹角,求光源投屏最高点到地面的距离结果精确到,参考数据:,,,
20.本小题分
如图,在中,、为弦,为直径,于,于,与相交于.
求证:;
若,,求的半径.
21.本小题分
瓜农李大爷为了解“品种西瓜”和“品种西瓜”的质量情况,从两大棚中分别随机调查个西瓜的质量单位:斤进行整理分析数据分为五组:,,,,,下面给出了部分信息:
“品种西瓜”质量统计表
质量斤 频数个 频率
“品种西瓜”,“品种西瓜”质量的平均数、中位数、众数、极差如下表:
品种 平均数 中位数 众数 极差
品种西瓜
品种西瓜
“品种西瓜”产量在组中的数据是:,,,,,,其余所有数据的和为.
根据以上信息,解答下列问题:
上述统计图表中, ______, ______, ______,扇形统计图组所对应扇形的圆心角度数为______;
根据以上数据,你认为哪种品种西瓜的质量情况更好?请说明理由;
若两个大棚种植的“品种西瓜”有个,“品种西瓜”有个,请估计质量在“”范围的西瓜的个数.
22.本小题分
已知二次函数.
求二次函数图象的对称轴以及与轴的交点坐标.
当时,的最大值与最小值的差为,求该二次函数的表达式.
若,直线经过抛物线的顶点,并与该抛物线的另一交点为点,当取最小值时,求的值.
23.本小题分
如图,在边长为的正方形中,,分别是边,上的点,连接,,.
若是的中点.
如图,当时,求证:.
如图,当时,求的值.
如图,延长,交于点,当,时,求证:.
2025年安徽省安庆市迎江区部分学校六月联考三模数学试卷答案和解析
一、选择题:本题共10小题,每小题4分,共40分。
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
二、填空题:本题共4小题,每小题5分,共20分。
11.
12.
13.
【解析】解:如图,取的中点,连接交于点,
,,,
,,,
,是等腰直角三角形,
四边形是矩形,
,,
,
,
∽,
,
,
,
由题意可得:,
,
∽,
,
.
故答案为:.
14.;
.
【解析】解:点,在抛物线的图象上,
,
,
二次函数的解析式为:,
故答案为:;
由知抛物线的解析式为,
抛物线向下平移个单位的解析式为,
顶点坐标为,
设直线的解析式为,
代入点,得到,
,
直线的解析式为,
时,,
使平移后抛物线顶点落在的内部不包括的边界,
,
.
故答案为:.
三、解答题:本题共9小题,共90分。
15.(8分)解:
.
16.(8分)解:如图,即为所求;
如图,即为所求,点的坐标.
17.(8分)安排了甲专车辆.
【解析】解:设安排了甲专车辆.
.
解得:.
答:安排了甲专车辆.
18.(8分);
;
.
【解析】解:由所给图形可知,
第个图案中“”的个数为:;
第个图案中“”的个数为:;
第个图案中“”的个数为:;
,
所以第个图案中“”的个数为个.
当时,
个,
即第个图案中“”的个数为个.
故答案为:.
由知,
第个图案中“”的个数为个.
由所给图形可知,
第个图案中最长的线段上“”的个数为,
第个图案中最长的线段上“”的个数为,
第个图案中最长的线段上“”的个数为,
,
所以第个图案中最长的线段上“”的个数为个.
19.(10分)解:延长交于点,过点作,垂足为,
由题意得:,,,,
,
,
在中,,,
,
,
,
在中,,
,
光源投屏最高点到地面的距离约为.
20.(10分)证明:如图,连接,
于,于,
又,
,
,
,
,
,
,
,
,
又,
;
解:如图,连接,设,则,
,
,
于,,
,
在中,,
即,
解得或舍.
即的半径为.
21.(12分),,,;
品种西瓜的质量情况更好,见解析;
大约有个.
【解析】解:由题意得,,
,
“品种西瓜”共个,根据扇形统计图可知:、共个,中位数是第、个,即在组最后个,即为:
;
组圆心角度数为:.
故答案为:,,,;
品种西瓜的质量情况更好,理由如下:
因为样本中“品种西瓜”的平均数、中位数、众数均高于“品种西瓜”,所以“品种西瓜”的质量情况更好;
个,
答:大约有个.
22.(12分)对称轴是直线,交点坐标为;
或;
.
【解析】解:已知二次函数,
二次函数图象的对称轴是直线.
当时,得,
二次函数图象与轴的交点坐标为;
若,抛物线开口向上,对称轴为直线,
,
当时,二次函数有最小值,
当时,二次函数有最大值,
,
解得,
该二次函数的表达式为.
若,抛物线开口向下,对称轴为直线,
当时,的最大值与最小值的差为,
当时,二次函数有最大值,
当时,二次函数有最小值,
,
解得,
该二次函数的表达式为,
综上所述,该二次函数的表达式为或;
由可得,二次函数图象的顶点坐标为.
直线经过抛物线的顶点,并与该抛物线的另一交点为点,
,
解得:,
.
联立得:,
解得或,
点.
设,则点,
,
,
,
当时,取最小值,
,即.
23.(14分)见解析;
;
见解析.
【解析】证明:四边形是正方形,
,.
是的中点,,
,
∽,
.
,
,
,
.
解:如图,延长交的延长线于点,过点作交的延长线于点.
,,
∽,
.
,,
.
设,.
在中,由勾股定理得:,
,
,
,
,
解得,
,,
在中,由勾股定理得:,
,
,
.
,
,
.
证明:如图,过点作,交的延长线于点.
设,,,
在中,由勾股定理得:,
.
,,
∽,
,
,
,.
在中,,
,
,
整理得,
解得:,
,
.
,
∽,
,
,
,
.
由由题意可得,证得∽,利用直角三角形的两个锐角互余即可得,可得结论;
延长交的延长线于点,过点作交的延长线于点证得∽,得,推得,设,,得,解得,可得,利用得,即可得;
过点作,交的延长线于点设,,,证得∽,即得,推得、,通过得,整理得一元二次方程,解得,再通过平行线分线段成比例得即可求解.
同课章节目录
