3.3.1指数函数的概念及其图象和性质 课件(共28张PPT) (北师大版2019必修第一册)
文档属性
| 名称 | 3.3.1指数函数的概念及其图象和性质 课件(共28张PPT) (北师大版2019必修第一册) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:51:58 | ||
图片预览







文档简介
(共28张PPT)
北师大版(2019)高中数学必修第一册
第三章 指数运算与指数函数
第3节 指数函数
3.3.1指数函数的概念及其图象和性质
导入课题
新知讲授
典例剖析
课堂小结
指数的故事
小明是百万富翁,一天,他碰到上一件奇怪的事.
一个叫小华的人对他说:“我想和你订个合同,我将在整整一个
月中每天给你10万元,而你第一天只需给我1分钱,以后你每天给我
的钱是前一天的两倍.”
小明欣喜若狂,觉得捡了个大便宜,立马地答应与小华签订合同.
大家想一想,小明是否真的捡了大便宜?
导入课题
新知讲授
典例剖析
课堂小结
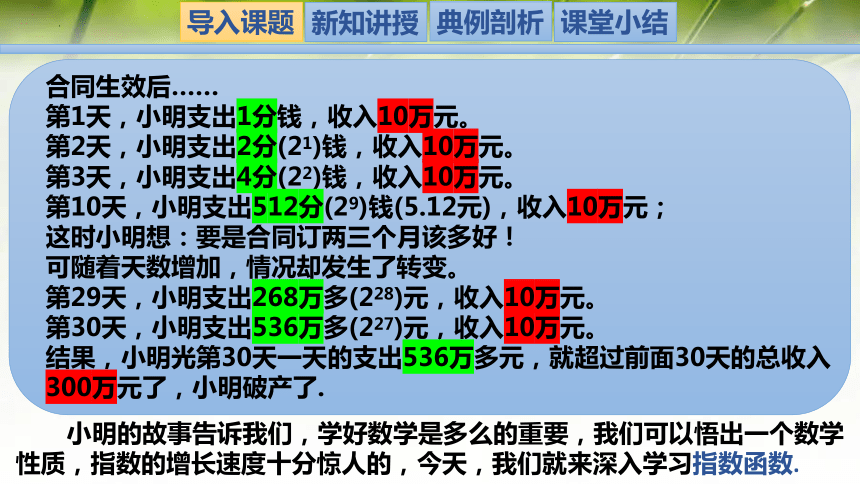
合同生效后……
第1天,小明支出1分钱,收入10万元。
第2天,小明支出2分(21)钱,收入10万元。
第3天,小明支出4分(22)钱,收入10万元。
第10天,小明支出512分(29)钱(5.12元),收入10万元;
这时小明想:要是合同订两三个月该多好!
可随着天数增加,情况却发生了转变。
第29天,小明支出268万多(228)元,收入10万元。
第30天,小明支出536万多(227)元,收入10万元。
结果,小明光第30天一天的支出536万多元,就超过前面30天的总收入
300万元了,小明破产了.
小明的故事告诉我们,学好数学是多么的重要,我们可以悟出一个数学性质,指数的增长速度十分惊人的,今天,我们就来深入学习指数函数.
一、指数函数的概念
导入课题
1,指数函数的概念:形如(且)的函数称为指数函数.
2,注意事项:①底数为常数,且;系数为1;
②指数x为自变量,定义域为.
③形如(k∈R且k≠1,且)的函数不是
指数函数,只能说是指数类型函数.
例如:①,是指数函数.
②,,
不是指数函数,只能说是指数类型函数.
新知探究
典例剖析
课堂小结
一、指数函数的概念
导入课题
3,为什么要规定且?
①当时,无研究意义;
②当时,若是分母为偶数的分数,在实数范围内,也无意义,例如
,……在实数范围内都是无意义的;
③当时,是一个常量,无研究意义.
新知探究
典例剖析
课堂小结
二、底数的指数函数的图象和性质
导入课题
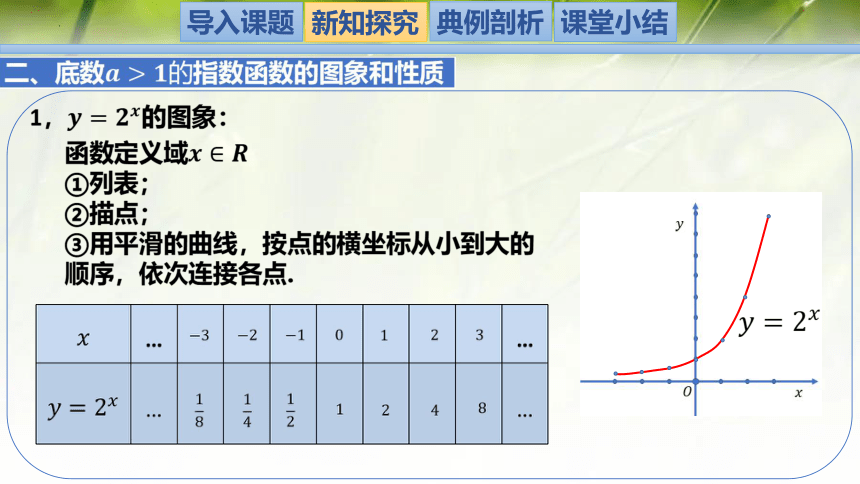
1,的图象:
新知探究
典例剖析
课堂小结
函数定义域
①列表;
②描点;
③用平滑的曲线,按点的横坐标从小到大的
顺序,依次连接各点.
导入课题
2,从的图象可以看出:
新知探究
典例剖析
课堂小结
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是增函数.
二、底数的指数函数的图象和性质
导入课题
3,函数与函数的图象的区别:
新知探究
典例剖析
课堂小结
用刚才的方法,我们可以做出的图象,
从图象可以看出:
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是增函数.
两个函数图象的区别是:
①在轴左侧,的图象在下方;
②在轴右侧,的图象在上方.
③底数越大时,随着的增大,的增长更快.
二、底数的指数函数的图象和性质
导入课题
4,的指数函数函数的图象和性质:
新知探究
典例剖析
课堂小结
一般的,指数函数(),
①定义域为,值域为,图象过定点;
②函数在上是增函数,
当时,
当时;
③对于指数函数和(),
当时,
当时,
当时.
二、底数的指数函数的图象和性质
导入课题
1,的图象:
新知探究
典例剖析
课堂小结
函数定义域
①列表;
②描点;
③用平滑的曲线,按点的横坐标从小到大的
顺序,依次连接各点.
三、底数的指数函数的图象和性质
导入课题
2,从的图象可以看出:
新知探究
典例剖析
课堂小结
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是减函数.
三、底数的指数函数的图象和性质
导入课题
3,函数与函数的图象的区别:
新知探究
典例剖析
课堂小结
用刚才的方法,我们可以做出的图象,从图象可以看出:
①函数的定义域为,值域为;
②函数过点;
③函数在上是减函数.
两个函数图象的区别是:
①在轴左侧,的图象在下方;
②在轴右侧,的图象在上方.
③底数越大时,随着的增大,的减小的越慢.
三、底数的指数函数的图象和性质
导入课题
4,底数的指数函数函数的图象和性质:
新知探究
典例剖析
课堂小结
一般的,指数函数(),
①定义域为,值域为,图象过定点;
②函数在上是减函数,
当时,
当时;
③对于指数函数和(),
当时,
当时,
当时.
三、底数的指数函数的图象和性质
解:
导入课题
新知探究
典例剖析
课堂小结
由指数函数()的性质可知,
函数在上是增函数,所以,
(1)∵,∴,
(2)∵,∴.
教材P83例题
例1 比较下列各题中两个数的大小:
(1); (2).
解:
导入课题
新知探究
典例剖析
课堂小结
(1)因为,所以,
又因为函数在上为增函数,所以,
所以实数的集合为;
(2)因为,所以,
所以,所以.
教材P83例题
例2 (1)求使不等式成立的实数的集合;
(2)已知方程,求实数的值.
解:
导入课题
新知探究
典例剖析
课堂小结
(1)∵指数函数在上为减函数,
且,∴;
(2)∵指数函数在上为减函数,
且,∴.
教材P86例题
例3 比较下列各题中两个数的大小:
(1); (2).
解:
导入课题
新知探究
典例剖析
课堂小结
(1)∵函数,而函数的值域为
,∴函数的值域为;
(2)∵函数,而函数在区间
上为减函数,∴其值域为,∴函数
在区间上的值域为.
教材P86例题
例4 求下列函数的值域:
(1); (2),.
导入课题
新知探究
典例剖析
课堂小结
练习1:某种细胞分裂时,由1个分裂成2个,由2个分裂成4个……一直分裂下去,请写出得到的细胞个数与分裂次数之间的函数关系式.
教材P84练习
解:依题意知,函数关系式为.
导入课题
新知探究
典例剖析
课堂小结
练习2:利用指数函数的图象由下列给定的的值,确定相应的函数值(结果精确到0.1):
并找出方程的近似解.
教材P84练习
解:因为,,,
,,,,
且2.828<5<8,
由函数在上为增函数得,
所以,所以区间上的任意一个数,都是方程的近似解,如.
导入课题
新知探究
典例剖析
课堂小结
练习3:比较下列各题中两个数的大小:
(1); (2).
教材P84练习
解:(1)因为函数在上为增函数,
且,所以;
(2)因为函数在上为增函数,
且,所以.
导入课题
新知探究
典例剖析
课堂小结
练习1:比较下列各题中两个数的大小:
(1); (2); (2); (2) .
教材P87练习
解:(1)∵函数在上为增函数,且,∴;
(2)∵函数在上为减函数,且,∴;
(3)∵函数在上为增函数,
且,,∴;
(4)∵函数,在上为增函数,∴,
由函数的图象可知,,
∴.
导入课题
新知探究
典例剖析
课堂小结
练习2:求使下列不等式成立的实数的集合:
(1); (2).
教材P87练习
解:(1)∵函数在上为增函数,且,
∴可转化为,∴∴;
(2)∵函数在上为减函数,且
∴,即,
又∵恒成立,
∴.
导入课题
新知探究
典例剖析
课堂小结
思考1:已知函数(为常数,且)为指数函数,
其图象经过点.求函数的解析式.
解:因为函数为指数函数,所以,
又因为其图象经过点,
所以,
所以
所以函数的解析式为
思考探究:指数函数的概念应用
导入课题
新知探究
典例剖析
课堂小结
思考2:解不等式;
解:不等式可转化为,
∵函数为增函数,
∴,解得
∴不等式的解集为.
思考探究:指数函数的概念应用
导入课题
新知探究
典例剖析
课堂小结
思考3:(多选)已知实数a,b满足等式2019a=2020b,则下列关系式中可能
成立的是( ).
A.0解:设2019a=2020b=t,作出y=2019x和y=2020x的图像如图所示,
由函数图像可得,
若t>1,则a>b>0,
若0若t=1,则a=b=0,
故B,C,D中关系式可能成立.
故选BCD.
思考探究:指数函数的图象和性质的应用
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
本节重点
思想方法
1,指数函数的图象与初中学习的函数图象不一样,熟练掌握指数函数的图象和性质,是解决后面复合函数问题的基础;
2,数形结合的思想方法:利用函数的性质解决方程、不等式等问题,是函数思想的重要应用;
一,指数函数的概念
1,指数函数的概念;2,注意事项
3,为什么要规定,且?
二,底数的指数函数的图象和性质
1,的图象
2,从的图象可以看出
3,函数与的区别
4,的指数函数的图象和性质
三,底数的指数函数的图象和性质
1,的图象
2,从的图象可以看出
3,函数与的区别
4,的指数函数的图象和性质
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:教材P89 A组T4
作业2:若函数f (x)=(a2-7a+7)ax是指数函数,求实数a的值.
谢谢聆听!
北师大版(2019)高中数学必修第一册
第三章 指数运算与指数函数
第3节 指数函数
3.3.1指数函数的概念及其图象和性质
导入课题
新知讲授
典例剖析
课堂小结
指数的故事
小明是百万富翁,一天,他碰到上一件奇怪的事.
一个叫小华的人对他说:“我想和你订个合同,我将在整整一个
月中每天给你10万元,而你第一天只需给我1分钱,以后你每天给我
的钱是前一天的两倍.”
小明欣喜若狂,觉得捡了个大便宜,立马地答应与小华签订合同.
大家想一想,小明是否真的捡了大便宜?
导入课题
新知讲授
典例剖析
课堂小结
合同生效后……
第1天,小明支出1分钱,收入10万元。
第2天,小明支出2分(21)钱,收入10万元。
第3天,小明支出4分(22)钱,收入10万元。
第10天,小明支出512分(29)钱(5.12元),收入10万元;
这时小明想:要是合同订两三个月该多好!
可随着天数增加,情况却发生了转变。
第29天,小明支出268万多(228)元,收入10万元。
第30天,小明支出536万多(227)元,收入10万元。
结果,小明光第30天一天的支出536万多元,就超过前面30天的总收入
300万元了,小明破产了.
小明的故事告诉我们,学好数学是多么的重要,我们可以悟出一个数学性质,指数的增长速度十分惊人的,今天,我们就来深入学习指数函数.
一、指数函数的概念
导入课题
1,指数函数的概念:形如(且)的函数称为指数函数.
2,注意事项:①底数为常数,且;系数为1;
②指数x为自变量,定义域为.
③形如(k∈R且k≠1,且)的函数不是
指数函数,只能说是指数类型函数.
例如:①,是指数函数.
②,,
不是指数函数,只能说是指数类型函数.
新知探究
典例剖析
课堂小结
一、指数函数的概念
导入课题
3,为什么要规定且?
①当时,无研究意义;
②当时,若是分母为偶数的分数,在实数范围内,也无意义,例如
,……在实数范围内都是无意义的;
③当时,是一个常量,无研究意义.
新知探究
典例剖析
课堂小结
二、底数的指数函数的图象和性质
导入课题
1,的图象:
新知探究
典例剖析
课堂小结
函数定义域
①列表;
②描点;
③用平滑的曲线,按点的横坐标从小到大的
顺序,依次连接各点.
导入课题
2,从的图象可以看出:
新知探究
典例剖析
课堂小结
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是增函数.
二、底数的指数函数的图象和性质
导入课题
3,函数与函数的图象的区别:
新知探究
典例剖析
课堂小结
用刚才的方法,我们可以做出的图象,
从图象可以看出:
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是增函数.
两个函数图象的区别是:
①在轴左侧,的图象在下方;
②在轴右侧,的图象在上方.
③底数越大时,随着的增大,的增长更快.
二、底数的指数函数的图象和性质
导入课题
4,的指数函数函数的图象和性质:
新知探究
典例剖析
课堂小结
一般的,指数函数(),
①定义域为,值域为,图象过定点;
②函数在上是增函数,
当时,
当时;
③对于指数函数和(),
当时,
当时,
当时.
二、底数的指数函数的图象和性质
导入课题
1,的图象:
新知探究
典例剖析
课堂小结
函数定义域
①列表;
②描点;
③用平滑的曲线,按点的横坐标从小到大的
顺序,依次连接各点.
三、底数的指数函数的图象和性质
导入课题
2,从的图象可以看出:
新知探究
典例剖析
课堂小结
①函数的定义域为;
②函数的值域为;
③函数过点;
④函数在上是减函数.
三、底数的指数函数的图象和性质
导入课题
3,函数与函数的图象的区别:
新知探究
典例剖析
课堂小结
用刚才的方法,我们可以做出的图象,从图象可以看出:
①函数的定义域为,值域为;
②函数过点;
③函数在上是减函数.
两个函数图象的区别是:
①在轴左侧,的图象在下方;
②在轴右侧,的图象在上方.
③底数越大时,随着的增大,的减小的越慢.
三、底数的指数函数的图象和性质
导入课题
4,底数的指数函数函数的图象和性质:
新知探究
典例剖析
课堂小结
一般的,指数函数(),
①定义域为,值域为,图象过定点;
②函数在上是减函数,
当时,
当时;
③对于指数函数和(),
当时,
当时,
当时.
三、底数的指数函数的图象和性质
解:
导入课题
新知探究
典例剖析
课堂小结
由指数函数()的性质可知,
函数在上是增函数,所以,
(1)∵,∴,
(2)∵,∴.
教材P83例题
例1 比较下列各题中两个数的大小:
(1); (2).
解:
导入课题
新知探究
典例剖析
课堂小结
(1)因为,所以,
又因为函数在上为增函数,所以,
所以实数的集合为;
(2)因为,所以,
所以,所以.
教材P83例题
例2 (1)求使不等式成立的实数的集合;
(2)已知方程,求实数的值.
解:
导入课题
新知探究
典例剖析
课堂小结
(1)∵指数函数在上为减函数,
且,∴;
(2)∵指数函数在上为减函数,
且,∴.
教材P86例题
例3 比较下列各题中两个数的大小:
(1); (2).
解:
导入课题
新知探究
典例剖析
课堂小结
(1)∵函数,而函数的值域为
,∴函数的值域为;
(2)∵函数,而函数在区间
上为减函数,∴其值域为,∴函数
在区间上的值域为.
教材P86例题
例4 求下列函数的值域:
(1); (2),.
导入课题
新知探究
典例剖析
课堂小结
练习1:某种细胞分裂时,由1个分裂成2个,由2个分裂成4个……一直分裂下去,请写出得到的细胞个数与分裂次数之间的函数关系式.
教材P84练习
解:依题意知,函数关系式为.
导入课题
新知探究
典例剖析
课堂小结
练习2:利用指数函数的图象由下列给定的的值,确定相应的函数值(结果精确到0.1):
并找出方程的近似解.
教材P84练习
解:因为,,,
,,,,
且2.828<5<8,
由函数在上为增函数得,
所以,所以区间上的任意一个数,都是方程的近似解,如.
导入课题
新知探究
典例剖析
课堂小结
练习3:比较下列各题中两个数的大小:
(1); (2).
教材P84练习
解:(1)因为函数在上为增函数,
且,所以;
(2)因为函数在上为增函数,
且,所以.
导入课题
新知探究
典例剖析
课堂小结
练习1:比较下列各题中两个数的大小:
(1); (2); (2); (2) .
教材P87练习
解:(1)∵函数在上为增函数,且,∴;
(2)∵函数在上为减函数,且,∴;
(3)∵函数在上为增函数,
且,,∴;
(4)∵函数,在上为增函数,∴,
由函数的图象可知,,
∴.
导入课题
新知探究
典例剖析
课堂小结
练习2:求使下列不等式成立的实数的集合:
(1); (2).
教材P87练习
解:(1)∵函数在上为增函数,且,
∴可转化为,∴∴;
(2)∵函数在上为减函数,且
∴,即,
又∵恒成立,
∴.
导入课题
新知探究
典例剖析
课堂小结
思考1:已知函数(为常数,且)为指数函数,
其图象经过点.求函数的解析式.
解:因为函数为指数函数,所以,
又因为其图象经过点,
所以,
所以
所以函数的解析式为
思考探究:指数函数的概念应用
导入课题
新知探究
典例剖析
课堂小结
思考2:解不等式;
解:不等式可转化为,
∵函数为增函数,
∴,解得
∴不等式的解集为.
思考探究:指数函数的概念应用
导入课题
新知探究
典例剖析
课堂小结
思考3:(多选)已知实数a,b满足等式2019a=2020b,则下列关系式中可能
成立的是( ).
A.0
由函数图像可得,
若t>1,则a>b>0,
若0
故B,C,D中关系式可能成立.
故选BCD.
思考探究:指数函数的图象和性质的应用
导入课题
新知探究
典例剖析
课堂小结
课堂
小结
本节重点
思想方法
1,指数函数的图象与初中学习的函数图象不一样,熟练掌握指数函数的图象和性质,是解决后面复合函数问题的基础;
2,数形结合的思想方法:利用函数的性质解决方程、不等式等问题,是函数思想的重要应用;
一,指数函数的概念
1,指数函数的概念;2,注意事项
3,为什么要规定,且?
二,底数的指数函数的图象和性质
1,的图象
2,从的图象可以看出
3,函数与的区别
4,的指数函数的图象和性质
三,底数的指数函数的图象和性质
1,的图象
2,从的图象可以看出
3,函数与的区别
4,的指数函数的图象和性质
导入课题
新知探究
典例剖析
课堂小结
课后作业
作业1:教材P89 A组T4
作业2:若函数f (x)=(a2-7a+7)ax是指数函数,求实数a的值.
谢谢聆听!
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
