专题07一次方程(组)及其应用(21题)(含答案+解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用)
文档属性
| 名称 | 专题07一次方程(组)及其应用(21题)(含答案+解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览



文档简介
专题07 一次方程(组)及其应用(21题)
一、单选题
1.(2025·天津·中考真题)《算学启蒙》是我国古代的数学著作,其中有一道题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”意思是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马天可以追上慢马,则可以列出的方程为( )
A. B.
C. D.
2.(2025·四川德阳·中考真题)在2000多年前的《九章算术》中记载了“共买鸡问题”:“今有共买鸡,人出九,盈十一;人出六,不足十六.问人数,物价各几何?”题意是:有若干人一起买鸡,如果每人出9文钱,就多11文钱;如果每人出6文钱,就差16文钱.问买鸡的人数,鸡的价钱各是多少?设买鸡的人数为x人,则x为( )
A.5 B.7 C.8 D.9
3.(2025·四川内江·中考真题)学校准备添置一批课桌椅,原订购60套,每套100元.店方表示:如果多购,可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.设每套课桌椅的成本为x元,则可列方程为( )
A. B.
C. D.
4.(2025·江苏连云港·中考真题)《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢 ”(凫:野鸭.所提问题即“野鸭与大雁从南海和北海同时起飞,经过多少天能够相遇 ”)如果设经过天能够相遇,根据题意,得( )
A. B. C. D.
5.(2025·山东烟台·中考真题)某商场打折销售一款风扇,若按标价的六折出售,则每台风扇亏损10元;若按标价的九折出售,则每台风扇盈利95元.这款风扇每台的标价为( )
A.350元 B.320元 C.270元 D.220元
二、填空题
6.(2025·四川宜宾·中考真题)已知、、、、是五个正整数去掉其中任意一个数,剩余四个数相加有五种情况,和却只有四个不同的值,分别是45、46、47、48,则 .
7.(2025·河北·中考真题)甲、乙两张等宽的长方形纸条,长分别为,.如图,将甲纸条的与乙纸条的叠合在一起,形成长为81的纸条,则 .
8.(2025·陕西·中考真题)草莓熟了,学校组织同学们参加劳动实践,帮助果农采摘草莓.小康和小悦采摘的时长相同,采摘结束后,小康采摘的草莓比小悦多.已知小康平均每小时采摘,小悦平均每小时采摘,小康采摘的时长是 小时.
9.(2025·江苏扬州·中考真题)如图1,棱长为的密封透明正方体容器水平放置在桌面上,其中水面高度.将此正方体放在坡角为的斜坡上,此时水面恰好与点齐平,其主视图如图2所示,则 .
10.(2025·四川德阳·中考真题)公元前世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”:阻力阻力臂动力动力臂.已知阻力和阻力臂分别为和,当动力为时,动力臂是 .
11.(2025·四川遂宁·中考真题)已知是方程的解,则 .
12.(2025·四川成都·中考真题)任意给一个数x,按下列程序进行计算.若输出的结果是15,则x的值为 .
三、解答题
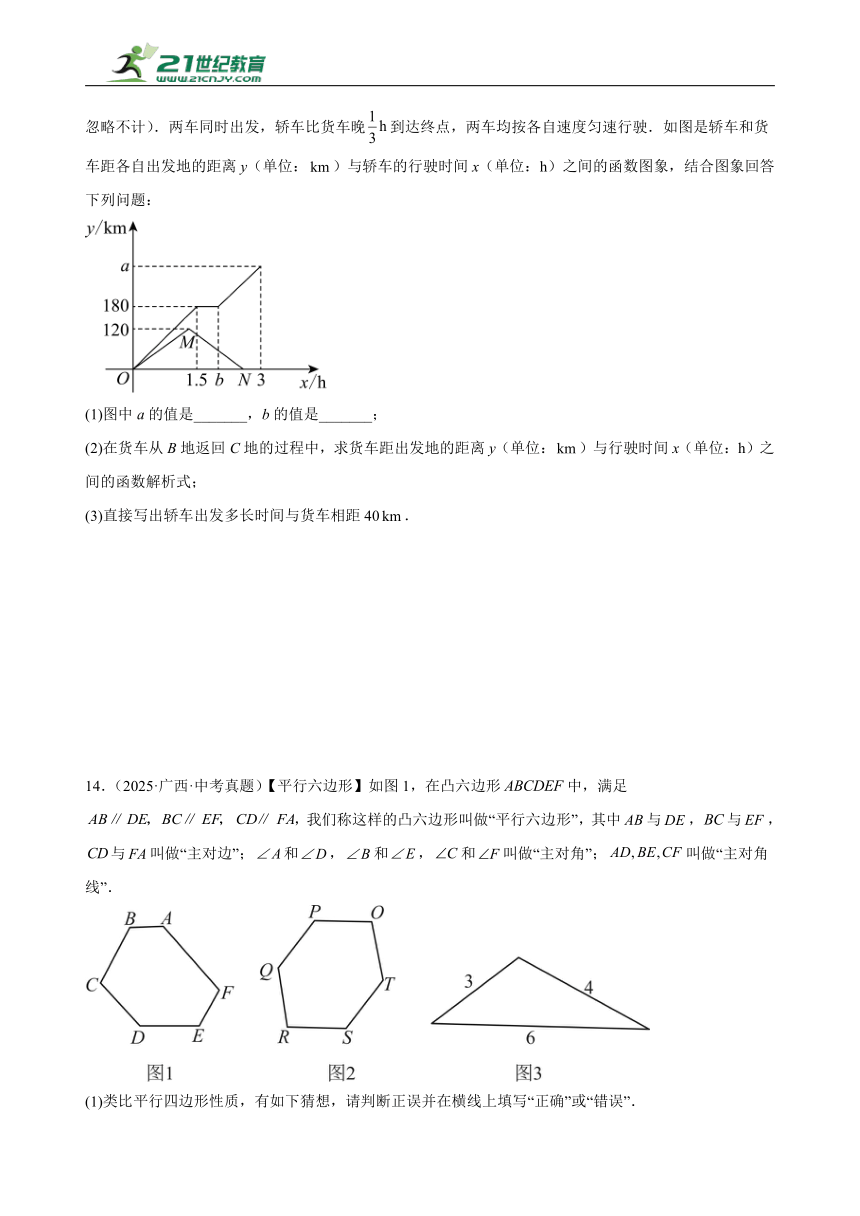
13.(2025·黑龙江·中考真题)一条公路上依次有A、B、C三地,一辆轿车从A地出发途经B地接人,停留一段时间后原速驶往C地;一辆货车从C地出发,送货到达B地后立即原路原速返回C地(卸货时间忽略不计).两车同时出发,轿车比货车晚到达终点,两车均按各自速度匀速行驶.如图是轿车和货车距各自出发地的距离y(单位:)与轿车的行驶时间x(单位:h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是_______,b的值是_______;
(2)在货车从B地返回C地的过程中,求货车距出发地的距离y(单位:)与行驶时间x(单位:h)之间的函数解析式;
(3)直接写出轿车出发多长时间与货车相距40.
14.(2025·广西·中考真题)【平行六边形】如图1,在凸六边形中,满足,我们称这样的凸六边形叫做“平行六边形”,其中与,与,与叫做“主对边”;和,和,和叫做“主对角”;叫做“主对角线”.
(1)类比平行四边形性质,有如下猜想,请判断正误并在横线上填写“正确”或“错误”.
猜想 判断正误
①平行六边形的三组主对边分别相等 _________
②平行六边形的三组主对角分别相等 _________
③平行六边形的三条主对角线互相平分 _________
【菱六边形】六条边都相等的平行六边形叫做“菱六边形”.
(2)如图2,已知平行六边形满足. 求证:平行六边形是菱六边形:
(3)如图3是一张边长为的三角形纸片.剪裁掉三个小三角形,使剪裁后的纸片为菱六边形.请在剪裁掉的小三角形中,任选一个,求它的各边长.
15.(2025·湖北·中考真题)某商店销售A,B两种水果.A水果标价14元/千克,B水果标价18元/千克.
(1)小明陪妈妈在这家商店按标价买了A,B两种水果共3千克,合计付款46元.这两种水果各买了多少千克?
(2)妈妈让小明再到这家商店买两种水果,要求B水果比A水果多买1千克,合计付款不超过50元.设小明买A水果千克.
①若这两种水果按标价出售,求的取值范围;
②小明到这家商店后,发现两种水果正在进行优惠活动:A水果打七五折;一次购买B水果不超过1千克不优惠,超过1千克后,超过1千克的部分打七五折.(注:“打七五折”指按标价的出售.)若小明合计付款48元,求的值.
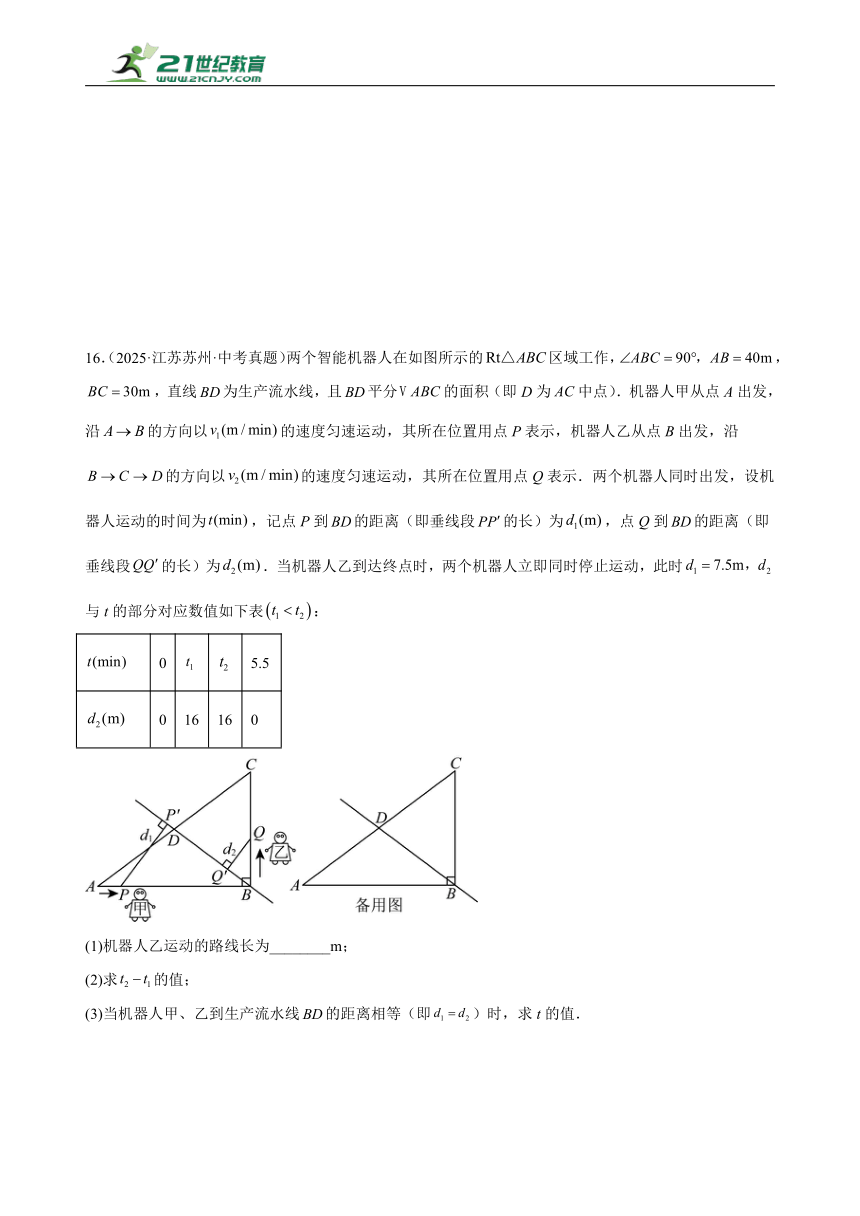
16.(2025·江苏苏州·中考真题)两个智能机器人在如图所示的区域工作,,,直线为生产流水线,且平分的面积(即D为中点).机器人甲从点A出发,沿的方向以的速度匀速运动,其所在位置用点P表示,机器人乙从点B出发,沿的方向以的速度匀速运动,其所在位置用点Q表示.两个机器人同时出发,设机器人运动的时间为,记点P到的距离(即垂线段的长)为,点Q到的距离(即垂线段的长)为.当机器人乙到达终点时,两个机器人立即同时停止运动,此时与t的部分对应数值如下表:
0 5.5
0 16 16 0
(1)机器人乙运动的路线长为________m;
(2)求的值;
(3)当机器人甲、乙到生产流水线的距离相等(即)时,求t的值.
17.(2025·江西·中考真题)系文物考古研究院用复原的青铜蒸馏器进行了蒸馏酒实验.用复原的青铜蒸馏器蒸馏粮食酒和芋头酒,需要的原材料与出酒率()如下表:
类别 原材料 出酒率
粮食酒 粮食糟醅(含大米、糯米、谷壳、大曲和蒸馏水 30%
芋头酒 芋头糟醅(含芋头、小曲和蒸馏水) 20%
如果第一次实验分别蒸馏出粮食酒和芋头酒共16公斤;第二次实验分别蒸馏出粮食酒和芋头酒共36公斤,且所用的粮食糟醅量是第一次的2倍,芋头糟醅量是第一次的3倍.
(1)求第一次实验分别用了多少公斤粮食糟醅和芋头糟醅?
(2)受限于当时的生产条件,古代青铜装馏器的出酒量约为现代复原品的80%.若粮食糟醅中大米占比约为,请问,在古代要想蒸馏出这两次实验得到的粮食酒总量,需要准备多少公斤大米?
18.(2025·四川眉山·中考真题)(1)计算:
(2)解方程:
19.(2025·山东·中考真题)山东省在能源绿色低碳转型过程中,探索出一条“以储调绿”的能源转型路径.某地结合实际情况,建立了一座圆柱形蓄水池,通过蓄水发电实现低峰蓄能、高峰释能,助力能源转型.
已知本次注水前蓄水池的水位高度为5米,注水时水位高度每小时上升6米.
(1)请写出本次注水过程中,蓄水池的水位高度y(米)与注水时间x(小时)之间的关系式;
(2)已知蓄水池的底面积为万平方米,每立方米的水可供发电千瓦时,求注水多长时间可供发电万千瓦时?
20.(2025·云南·中考真题)已知是常数,函数,记.
(1)若,,求的值;
(2)若,,比较与的大小.
21.(2025·重庆·中考真题)列方程解下列问题:
某厂生产甲、乙两种文创产品.每天生产甲种文创产品的数量比每天生产乙种文创产品的数量多50个,3天时间生产的甲种文创产品的数量比4天时间生产的乙种文创产品的数量多100个.
(1)求该厂每天生产的甲、乙文创产品数量分别是多少个?
(2)由于市场需求量增加,该厂对生产流程进行了改进.改进后,每天生产乙种文创产品的数量较改进前每天生产的数量增加同样的数量,且每天生产甲种文创产品的数量较改进前每天增加的数量是乙种文创产品每天增加数量的2倍.若生产甲、乙两种文创产品各1400个,乙比甲多用10天,求每天生产的乙种文创产品增加的数量.
《专题07 一次方程(组)及其应用(21题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5
答案 A D B A A
1.A
本题考查一元一次方程的应用,属于行程问题中的追及问题.解题的关键是找到两马路程相等的等量关系.
设快马用天追上慢马,快马的总路程为里,慢马的总路程为里,根据题意,列出方程即可.
解:设快马用天追上慢马,快马的总路程为里,慢马的总路程为里,根据题意得:
.
故选:A
2.D
设买鸡的人数为,根据两种不同出钱方式下鸡的价钱不变这一关系,分别表示出两种情况下鸡的价钱,建立方程求解即可.本题主要考查了一元一次方程的实际应用,熟练掌握根据实际问题中的等量关系(鸡的价钱不变 )建立方程求解是解题的关键.
根据题意,每人出9文钱时,总钱数为文,多出11文,故鸡的价钱为文;
每人出6文钱时,总钱数为文,不足16文,故鸡的价钱为文.
列方程:
解得:
故买鸡的人数为9人,
故选:D.
3.B
本题考查了一元一次方程的应用,根据利润相等建立方程.原计划利润为,实际利润为,两者相等即可求解.
解:设每套成本为元.原计划利润为元;实际购买时利润为元.
根据题意得:,
故选B.
4.A
本题考查的是一元一次方程的应用,属于相遇问题,需根据两者相向而行,相遇时路程之和为全程(即1),再建立方程即可.
解:设相遇时间为天,野鸭从南海到北海需7天,故其速度为(全程/天);
大雁从北海到南海需9天,故其速度为(全程/天),
∴方程为,
故选:A
5.A
本题主要考查了一元一次方程的实际应用,设这款风扇每台的标价为元,根据按标价的六折出售,则每台风扇亏损10元可得风扇的进价为元,根据按标价的九折出售,则每台风扇盈利95元可得风扇的进价为元,据此建立方程求解即可.
解:设这款风扇每台的标价为元,
由题意得,,
解得,
∴这款风扇每台的标价为350元,
故选:A.
6.58
本题主要考查了整式的加减运算、一元一次方程的应用等知识点,掌握分类讨论思想是解题的关键.
设,由题意可知已知这五个和只有四个不同的值,不妨设,那么这四个不同的值可以表示为(假设与前面某一个数相等)且为这四个值分别是45、46、47、48;再说明,然后分四种情况解答即可.
解:设,那么去掉后和为;去掉后和为;去掉后和为;去掉后和为;去掉后和为;
∵已知这五个和只有四个不同的值,
∴不妨设,
那么这四个不同的值可以表示为(假设与前面某一个数相等).
∵这四个值分别是45、46、47、48,
∴,即,
∵
∴,
∴,即;
当时,即;
∴,解得:,不是整数,不符合题意;
当时,即;
∴,解得:,符合题意;
当时,即;
∴,解得:,不是整数,不符合题意;
当时,即;
∴,解得:,不是整数,不符合题意;
综上,,即.
故答案为:58.
7.99
本题主要考查了已知式子的值求代数式的值,一元一次方程的应用,由题意可知:重叠部分为: ,设叠部分的长度为k,则,,根据重叠后的总长度为81为等量关系列出关于k的一元一次方程,求解即可得出答案.
解:由题意可知:重叠部分为: ,
设重叠部分的长度为k,则,,
重叠后的总长度为:,即,
代入,得:,
解得:,
∴,,
∴,
故答案为:99.
8.
此题主要考查了一元一次方程的应用,根据采摘的质量得出等式是解题关键.利用小康采摘的草莓比小悦多得出等式求出答案.
解:设两小组采摘了小时,
依题意:,
解得:,
因此,两小组采摘了小时.
故答案为:.
9.
本题考查了求角的正切值、一元一次方程的几何应用、主视图、平行线的性质等知识,熟练掌握正切的定义是解题关键.延长,交直线于点,设,则,先根据水的体积不变建立方程,解方程可得的值,再根据平行线的性质可得,然后根据正切的定义计算即可得.
解:如图,延长,交直线于点,
由题意得:,
设,则,
∵密封透明正方体容器水平放置在桌面上与放在坡角为的斜坡上,容器里水的体积不变;且放在坡角为的斜坡上时,水的体积等于长为、宽为、高为的长方体的体积与长为、宽为、高为的长方体的体积的一半之和,
∴,
解得,
即,
∵,
∴,
∵,
∴,
∴,
故答案为:.
10./
本题考查了一元一次方程的应用,设动力臂是,根据“阻力阻力臂动力动力臂”列出方程,然后解方程即可,读懂题意,列出方程是解题的关键.
解:设动力臂是,
由题意得:,
解得:,
故答案为:.
11.2
本题考查了一元一次方程的解,以及解一元一次方程,理解题意,把代入,解得,即可作答.
解:∵是方程的解,
∴把代入,得,
∴,
∴,
故答案为:2
12.3
本题考查了程序框图的计算,一元一次方程的应用,正确理解题意是解题的关键.
根据程序框图的运算法则建立一元方程求解即可.
解:由题意得:,
解得:,
故答案为:3.
13.(1)300,2
(2)
(3)或或
本题考查一次函数的实际应用,从函数图象中有效的获取信息,正确的求出函数解析式,是解题的关键:
(1)根据货车的图象得到B、C两地的距离为,进而求出的值,求出轿车的速度,求出轿车从开往地所需的时间,进而求出的值;
(2)根据轿车比货车晚到达终点,求出点坐标,进而求出点坐标,待定系数法求出函数解析式即可;
(3)分轿车到达地之前,轿车到达地,货车离地,以及货车到达地时,三种情况进行讨论求解即可.
(1)解:由图象可知,B、C两地的距离为,A、B两地的距离为,
∴,
∵轿车的速度为:,
∴轿车从开往地所需的时间为:,
∴;
故答案为:300,2;
(2)∵轿车比货车晚到达终点,
∴货车到达地所用时间为:,
∴,
∵货车从C地出发,送货到达B地后立即原路原速返回C地,
∴,
设,
∴,解得:,
∴;
(3)由(2)可知,货车的速度为:,
∴当轿车到达地之前,,解得:;
当轿车到达地,货车离地时,,则:符合题意;
当货车到达地时,此时轿车离点的距离为:,恰好满足题意,此时;
综上:轿车出发或或时与货车相距40.
14.(1)错误;正确;错误
(2)详见解析
(3)
本题考查了平行四边形的性质与判定、相似三角形的性质与判定以及解方程:(1)连接,根据相似三角形和平行线的性质即可判断;(2)先证明为平行四边形,再证明为平行四边形,即可证明是菱六边形;(3)根据菱六边形得到,设,根据解得,代入即可.
(1)解:连接,交于点,由图可知:
①平行于,只能知道,其他对边同理,故平行六边形的三组主对边分别相等是错误的;
②平行于,,同理可得,其他对角同理,故平行六边形的三组主对角分别相等是正确的;
③由①可知,平行六边形的三条主对角线互相平分是错误的.
(2)证明:过点作平行且相等于,连接,
则平行四边形是平行四边形,
平行于,,
在平行六边形中,平行于,,
平行且相等于,
为平行四边形,
平行于,,
在平行六边形中,平行于,平行于,
平行于,平行于,
为平行四边形,
,
,
,
,
平行六边形是菱六边形.
(3)解:设三角形纸片为,
裁剪后的纸片为菱六边形,
平行于,平行于,平行于,,
,
,
设,
则,
,
,
,
解得:,
.
15.(1)购买A种水果2千克,B种水果1千克
(2)①;②
本题考查的是一元一次方程的应用,一元一次不等式的应用,二元一次方程组的应用;
(1)设购买A种水果x千克,B种水果y千克,根据在这家商店按标价买了A,B两种水果共3千克,合计付款46元.再建立方程组解题即可;
(2)①设小明买A水果千克,则B种水果购买了千克,根据要求B水果比A水果多买1千克,合计付款不超过50元,再建立不等式求解即可;②设小明买A水果千克,则B种水果购买了千克,根据不同的优惠方式可得,再解方程即可.
(1)解:设购买A种水果x千克,B种水果y千克,
依题意得:,
解得:.
答:购买A种水果2千克,B种水果1千克.
(2)解:①设小明买A水果千克,则B种水果购买了千克,
∴,
解得:,
∴结合实际可得:;
②设小明买A水果千克,则B种水果购买了千克,
∴,
解得:.
16.(1)55
(2)
(3)或
(1)利用勾股定理求解即可;
(2)利用直角三角形斜边中线的性质求得,得到,,推出,,分当点Q在上和点Q在上时,两种情况讨论,分别求得,,据此求解即可;
(3)根据题意求得,分当点Q在上和点Q在上时两种情况讨论,列式一元一次方程方程,求解即可.
(1)解:∵,,
∴,
∵D为中点,
∴,
∵,
∴机器人乙运动的路线长为,
故答案为:55;
(2)解:根据题意,得,
∵中,,为中点,
∴,
∴,,
∴,,
当点Q在上时,,
∴,解得,
当点Q在上时,作,垂足为H(如图),
则.
∵,
∴,
∴,
∴,
解得,
∴;
(3)解:当时,,
此时,,
∴,
∴,
∴,
当点Q在上时,由,得,
解得.
当点Q在上时,由,得,
解得.
∴或.
本题考查了解直角三角形的应用,勾股定理,一元一次方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件.
17.(1)第一次实验用粮食糟醅和芋头糟醅的质量分别是40、20公斤.
(2)需要准备公斤大米.
本题主要考查了二元一次方程组、一元一次方程的应用等知识点,审清题意、正确列出方程组和方程是解题的关键.
(1)第一次实验用粮食糟醅和芋头糟醅的质量分别是x、y公斤,则第一次实验用粮食糟醅和芋头糟醅的质量分别是公斤,然后根据题意列二元一次方程组求解即可;
(2)先求出两次得到粮食酒的总质量,设需要准备z公斤大米,则粮食糟醅的质量为,再根据题意列一元一次方程求解即可.
(1)解:第一次实验用粮食糟醅和芋头糟醅的质量分别是x、y公斤,则第一次实验用粮食糟醅和芋头糟醅的质量分别是公斤,
由题意可得:,解得:.
答:第一次实验用粮食糟醅和芋头糟醅的质量分别是40、20公斤.
(2)解:两次实验得到的粮食酒总量为公斤,
设需要准备z公斤大米,则粮食糟醅的质量为,
由题意可得:,解得:千克.
答:需要准备公斤大米.
18.(1)(2)
本题考查实数的运算,解一元一次方程,熟练掌握相关运算法则,解一元一次方程的步骤,是解题的关键:
(1)先开方,去绝对值,再进行加减运算即可;
(2)去括号,移项,合并,系数化1,进行计算即可.
解:(1)原式;
(2)去括号,得:,
移项,得:,
合并,得:.
19.(1)
(2)注水5小时可供发电万千瓦时.
本题考查一次函数的应用、一元一次方程的应用等知识点,正确列出函数解析式和方程是解题的关键.
(1)根据蓄水池的水位高度等于注水时水位每小时升高的高度乘以注水时间与本次注水前蓄水池的水位高度的和,据此列出函数关系式即可;
(2)根据y与x的函数关系式以及已知条件列关于x的一元一次方程并求解即可.
(1)解:由题意可得:蓄水池的水位高度y(米)与注水时间x(小时)之间的关系式.
(2)解:根据题意,得,
解得.
答:注水5小时可供发电万千瓦时.
20.(1)的值为;
(2)当时,;当时,.
本题考查了分式求值,等式的性质,函数求值,掌握知识点的应用是解题的关键.
()把,代入函数即可求解;
()将,代入函数整理得,然后分当时,即和当时两种情况求解即可.
(1)解:把,代入函数得,
,
∴的值为;
(2)解:将,代入函数得,
,
整理得:,
当时,即,
∴,
当时,,
则有,,
,
∴
,
综上可知:当时,;当时,.
21.(1)该厂每天生产的甲文创产品数量为个,乙文创产品数量是个
(2)每天乙文创产品增加的数量是个
本题考查一元一次方程和分式方程的应用,正确理解题意,根据等量关系列方程是解题的关键.
(1)设该厂每天生产的乙文创产品数量是x个,根据题意列一元一次方程解答即可;
(2)设该厂每天乙文创产品增加的数量是个,根据“生产甲、乙两种文创产品各1400个,乙比甲多用10天”列分式方程解答即可.
(1)解:设该厂每天生产的乙文创产品数量是x个,则甲文创产品数量为个.
,
解得:,
则甲文创产品数量为个,
答:该厂每天生产的乙文创产品数量是个,则甲文创产品数量为个.
(2)解:设每天乙文创产品增加的数量是个,则甲文创产品增加的数量是个.
,
解得:,
经检验:是原方程的解,
答:每天乙文创产品增加的数量是个.
一、单选题
1.(2025·天津·中考真题)《算学启蒙》是我国古代的数学著作,其中有一道题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”意思是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马天可以追上慢马,则可以列出的方程为( )
A. B.
C. D.
2.(2025·四川德阳·中考真题)在2000多年前的《九章算术》中记载了“共买鸡问题”:“今有共买鸡,人出九,盈十一;人出六,不足十六.问人数,物价各几何?”题意是:有若干人一起买鸡,如果每人出9文钱,就多11文钱;如果每人出6文钱,就差16文钱.问买鸡的人数,鸡的价钱各是多少?设买鸡的人数为x人,则x为( )
A.5 B.7 C.8 D.9
3.(2025·四川内江·中考真题)学校准备添置一批课桌椅,原订购60套,每套100元.店方表示:如果多购,可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.设每套课桌椅的成本为x元,则可列方程为( )
A. B.
C. D.
4.(2025·江苏连云港·中考真题)《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢 ”(凫:野鸭.所提问题即“野鸭与大雁从南海和北海同时起飞,经过多少天能够相遇 ”)如果设经过天能够相遇,根据题意,得( )
A. B. C. D.
5.(2025·山东烟台·中考真题)某商场打折销售一款风扇,若按标价的六折出售,则每台风扇亏损10元;若按标价的九折出售,则每台风扇盈利95元.这款风扇每台的标价为( )
A.350元 B.320元 C.270元 D.220元
二、填空题
6.(2025·四川宜宾·中考真题)已知、、、、是五个正整数去掉其中任意一个数,剩余四个数相加有五种情况,和却只有四个不同的值,分别是45、46、47、48,则 .
7.(2025·河北·中考真题)甲、乙两张等宽的长方形纸条,长分别为,.如图,将甲纸条的与乙纸条的叠合在一起,形成长为81的纸条,则 .
8.(2025·陕西·中考真题)草莓熟了,学校组织同学们参加劳动实践,帮助果农采摘草莓.小康和小悦采摘的时长相同,采摘结束后,小康采摘的草莓比小悦多.已知小康平均每小时采摘,小悦平均每小时采摘,小康采摘的时长是 小时.
9.(2025·江苏扬州·中考真题)如图1,棱长为的密封透明正方体容器水平放置在桌面上,其中水面高度.将此正方体放在坡角为的斜坡上,此时水面恰好与点齐平,其主视图如图2所示,则 .
10.(2025·四川德阳·中考真题)公元前世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”:阻力阻力臂动力动力臂.已知阻力和阻力臂分别为和,当动力为时,动力臂是 .
11.(2025·四川遂宁·中考真题)已知是方程的解,则 .
12.(2025·四川成都·中考真题)任意给一个数x,按下列程序进行计算.若输出的结果是15,则x的值为 .
三、解答题
13.(2025·黑龙江·中考真题)一条公路上依次有A、B、C三地,一辆轿车从A地出发途经B地接人,停留一段时间后原速驶往C地;一辆货车从C地出发,送货到达B地后立即原路原速返回C地(卸货时间忽略不计).两车同时出发,轿车比货车晚到达终点,两车均按各自速度匀速行驶.如图是轿车和货车距各自出发地的距离y(单位:)与轿车的行驶时间x(单位:h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是_______,b的值是_______;
(2)在货车从B地返回C地的过程中,求货车距出发地的距离y(单位:)与行驶时间x(单位:h)之间的函数解析式;
(3)直接写出轿车出发多长时间与货车相距40.
14.(2025·广西·中考真题)【平行六边形】如图1,在凸六边形中,满足,我们称这样的凸六边形叫做“平行六边形”,其中与,与,与叫做“主对边”;和,和,和叫做“主对角”;叫做“主对角线”.
(1)类比平行四边形性质,有如下猜想,请判断正误并在横线上填写“正确”或“错误”.
猜想 判断正误
①平行六边形的三组主对边分别相等 _________
②平行六边形的三组主对角分别相等 _________
③平行六边形的三条主对角线互相平分 _________
【菱六边形】六条边都相等的平行六边形叫做“菱六边形”.
(2)如图2,已知平行六边形满足. 求证:平行六边形是菱六边形:
(3)如图3是一张边长为的三角形纸片.剪裁掉三个小三角形,使剪裁后的纸片为菱六边形.请在剪裁掉的小三角形中,任选一个,求它的各边长.
15.(2025·湖北·中考真题)某商店销售A,B两种水果.A水果标价14元/千克,B水果标价18元/千克.
(1)小明陪妈妈在这家商店按标价买了A,B两种水果共3千克,合计付款46元.这两种水果各买了多少千克?
(2)妈妈让小明再到这家商店买两种水果,要求B水果比A水果多买1千克,合计付款不超过50元.设小明买A水果千克.
①若这两种水果按标价出售,求的取值范围;
②小明到这家商店后,发现两种水果正在进行优惠活动:A水果打七五折;一次购买B水果不超过1千克不优惠,超过1千克后,超过1千克的部分打七五折.(注:“打七五折”指按标价的出售.)若小明合计付款48元,求的值.
16.(2025·江苏苏州·中考真题)两个智能机器人在如图所示的区域工作,,,直线为生产流水线,且平分的面积(即D为中点).机器人甲从点A出发,沿的方向以的速度匀速运动,其所在位置用点P表示,机器人乙从点B出发,沿的方向以的速度匀速运动,其所在位置用点Q表示.两个机器人同时出发,设机器人运动的时间为,记点P到的距离(即垂线段的长)为,点Q到的距离(即垂线段的长)为.当机器人乙到达终点时,两个机器人立即同时停止运动,此时与t的部分对应数值如下表:
0 5.5
0 16 16 0
(1)机器人乙运动的路线长为________m;
(2)求的值;
(3)当机器人甲、乙到生产流水线的距离相等(即)时,求t的值.
17.(2025·江西·中考真题)系文物考古研究院用复原的青铜蒸馏器进行了蒸馏酒实验.用复原的青铜蒸馏器蒸馏粮食酒和芋头酒,需要的原材料与出酒率()如下表:
类别 原材料 出酒率
粮食酒 粮食糟醅(含大米、糯米、谷壳、大曲和蒸馏水 30%
芋头酒 芋头糟醅(含芋头、小曲和蒸馏水) 20%
如果第一次实验分别蒸馏出粮食酒和芋头酒共16公斤;第二次实验分别蒸馏出粮食酒和芋头酒共36公斤,且所用的粮食糟醅量是第一次的2倍,芋头糟醅量是第一次的3倍.
(1)求第一次实验分别用了多少公斤粮食糟醅和芋头糟醅?
(2)受限于当时的生产条件,古代青铜装馏器的出酒量约为现代复原品的80%.若粮食糟醅中大米占比约为,请问,在古代要想蒸馏出这两次实验得到的粮食酒总量,需要准备多少公斤大米?
18.(2025·四川眉山·中考真题)(1)计算:
(2)解方程:
19.(2025·山东·中考真题)山东省在能源绿色低碳转型过程中,探索出一条“以储调绿”的能源转型路径.某地结合实际情况,建立了一座圆柱形蓄水池,通过蓄水发电实现低峰蓄能、高峰释能,助力能源转型.
已知本次注水前蓄水池的水位高度为5米,注水时水位高度每小时上升6米.
(1)请写出本次注水过程中,蓄水池的水位高度y(米)与注水时间x(小时)之间的关系式;
(2)已知蓄水池的底面积为万平方米,每立方米的水可供发电千瓦时,求注水多长时间可供发电万千瓦时?
20.(2025·云南·中考真题)已知是常数,函数,记.
(1)若,,求的值;
(2)若,,比较与的大小.
21.(2025·重庆·中考真题)列方程解下列问题:
某厂生产甲、乙两种文创产品.每天生产甲种文创产品的数量比每天生产乙种文创产品的数量多50个,3天时间生产的甲种文创产品的数量比4天时间生产的乙种文创产品的数量多100个.
(1)求该厂每天生产的甲、乙文创产品数量分别是多少个?
(2)由于市场需求量增加,该厂对生产流程进行了改进.改进后,每天生产乙种文创产品的数量较改进前每天生产的数量增加同样的数量,且每天生产甲种文创产品的数量较改进前每天增加的数量是乙种文创产品每天增加数量的2倍.若生产甲、乙两种文创产品各1400个,乙比甲多用10天,求每天生产的乙种文创产品增加的数量.
《专题07 一次方程(组)及其应用(21题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5
答案 A D B A A
1.A
本题考查一元一次方程的应用,属于行程问题中的追及问题.解题的关键是找到两马路程相等的等量关系.
设快马用天追上慢马,快马的总路程为里,慢马的总路程为里,根据题意,列出方程即可.
解:设快马用天追上慢马,快马的总路程为里,慢马的总路程为里,根据题意得:
.
故选:A
2.D
设买鸡的人数为,根据两种不同出钱方式下鸡的价钱不变这一关系,分别表示出两种情况下鸡的价钱,建立方程求解即可.本题主要考查了一元一次方程的实际应用,熟练掌握根据实际问题中的等量关系(鸡的价钱不变 )建立方程求解是解题的关键.
根据题意,每人出9文钱时,总钱数为文,多出11文,故鸡的价钱为文;
每人出6文钱时,总钱数为文,不足16文,故鸡的价钱为文.
列方程:
解得:
故买鸡的人数为9人,
故选:D.
3.B
本题考查了一元一次方程的应用,根据利润相等建立方程.原计划利润为,实际利润为,两者相等即可求解.
解:设每套成本为元.原计划利润为元;实际购买时利润为元.
根据题意得:,
故选B.
4.A
本题考查的是一元一次方程的应用,属于相遇问题,需根据两者相向而行,相遇时路程之和为全程(即1),再建立方程即可.
解:设相遇时间为天,野鸭从南海到北海需7天,故其速度为(全程/天);
大雁从北海到南海需9天,故其速度为(全程/天),
∴方程为,
故选:A
5.A
本题主要考查了一元一次方程的实际应用,设这款风扇每台的标价为元,根据按标价的六折出售,则每台风扇亏损10元可得风扇的进价为元,根据按标价的九折出售,则每台风扇盈利95元可得风扇的进价为元,据此建立方程求解即可.
解:设这款风扇每台的标价为元,
由题意得,,
解得,
∴这款风扇每台的标价为350元,
故选:A.
6.58
本题主要考查了整式的加减运算、一元一次方程的应用等知识点,掌握分类讨论思想是解题的关键.
设,由题意可知已知这五个和只有四个不同的值,不妨设,那么这四个不同的值可以表示为(假设与前面某一个数相等)且为这四个值分别是45、46、47、48;再说明,然后分四种情况解答即可.
解:设,那么去掉后和为;去掉后和为;去掉后和为;去掉后和为;去掉后和为;
∵已知这五个和只有四个不同的值,
∴不妨设,
那么这四个不同的值可以表示为(假设与前面某一个数相等).
∵这四个值分别是45、46、47、48,
∴,即,
∵
∴,
∴,即;
当时,即;
∴,解得:,不是整数,不符合题意;
当时,即;
∴,解得:,符合题意;
当时,即;
∴,解得:,不是整数,不符合题意;
当时,即;
∴,解得:,不是整数,不符合题意;
综上,,即.
故答案为:58.
7.99
本题主要考查了已知式子的值求代数式的值,一元一次方程的应用,由题意可知:重叠部分为: ,设叠部分的长度为k,则,,根据重叠后的总长度为81为等量关系列出关于k的一元一次方程,求解即可得出答案.
解:由题意可知:重叠部分为: ,
设重叠部分的长度为k,则,,
重叠后的总长度为:,即,
代入,得:,
解得:,
∴,,
∴,
故答案为:99.
8.
此题主要考查了一元一次方程的应用,根据采摘的质量得出等式是解题关键.利用小康采摘的草莓比小悦多得出等式求出答案.
解:设两小组采摘了小时,
依题意:,
解得:,
因此,两小组采摘了小时.
故答案为:.
9.
本题考查了求角的正切值、一元一次方程的几何应用、主视图、平行线的性质等知识,熟练掌握正切的定义是解题关键.延长,交直线于点,设,则,先根据水的体积不变建立方程,解方程可得的值,再根据平行线的性质可得,然后根据正切的定义计算即可得.
解:如图,延长,交直线于点,
由题意得:,
设,则,
∵密封透明正方体容器水平放置在桌面上与放在坡角为的斜坡上,容器里水的体积不变;且放在坡角为的斜坡上时,水的体积等于长为、宽为、高为的长方体的体积与长为、宽为、高为的长方体的体积的一半之和,
∴,
解得,
即,
∵,
∴,
∵,
∴,
∴,
故答案为:.
10./
本题考查了一元一次方程的应用,设动力臂是,根据“阻力阻力臂动力动力臂”列出方程,然后解方程即可,读懂题意,列出方程是解题的关键.
解:设动力臂是,
由题意得:,
解得:,
故答案为:.
11.2
本题考查了一元一次方程的解,以及解一元一次方程,理解题意,把代入,解得,即可作答.
解:∵是方程的解,
∴把代入,得,
∴,
∴,
故答案为:2
12.3
本题考查了程序框图的计算,一元一次方程的应用,正确理解题意是解题的关键.
根据程序框图的运算法则建立一元方程求解即可.
解:由题意得:,
解得:,
故答案为:3.
13.(1)300,2
(2)
(3)或或
本题考查一次函数的实际应用,从函数图象中有效的获取信息,正确的求出函数解析式,是解题的关键:
(1)根据货车的图象得到B、C两地的距离为,进而求出的值,求出轿车的速度,求出轿车从开往地所需的时间,进而求出的值;
(2)根据轿车比货车晚到达终点,求出点坐标,进而求出点坐标,待定系数法求出函数解析式即可;
(3)分轿车到达地之前,轿车到达地,货车离地,以及货车到达地时,三种情况进行讨论求解即可.
(1)解:由图象可知,B、C两地的距离为,A、B两地的距离为,
∴,
∵轿车的速度为:,
∴轿车从开往地所需的时间为:,
∴;
故答案为:300,2;
(2)∵轿车比货车晚到达终点,
∴货车到达地所用时间为:,
∴,
∵货车从C地出发,送货到达B地后立即原路原速返回C地,
∴,
设,
∴,解得:,
∴;
(3)由(2)可知,货车的速度为:,
∴当轿车到达地之前,,解得:;
当轿车到达地,货车离地时,,则:符合题意;
当货车到达地时,此时轿车离点的距离为:,恰好满足题意,此时;
综上:轿车出发或或时与货车相距40.
14.(1)错误;正确;错误
(2)详见解析
(3)
本题考查了平行四边形的性质与判定、相似三角形的性质与判定以及解方程:(1)连接,根据相似三角形和平行线的性质即可判断;(2)先证明为平行四边形,再证明为平行四边形,即可证明是菱六边形;(3)根据菱六边形得到,设,根据解得,代入即可.
(1)解:连接,交于点,由图可知:
①平行于,只能知道,其他对边同理,故平行六边形的三组主对边分别相等是错误的;
②平行于,,同理可得,其他对角同理,故平行六边形的三组主对角分别相等是正确的;
③由①可知,平行六边形的三条主对角线互相平分是错误的.
(2)证明:过点作平行且相等于,连接,
则平行四边形是平行四边形,
平行于,,
在平行六边形中,平行于,,
平行且相等于,
为平行四边形,
平行于,,
在平行六边形中,平行于,平行于,
平行于,平行于,
为平行四边形,
,
,
,
,
平行六边形是菱六边形.
(3)解:设三角形纸片为,
裁剪后的纸片为菱六边形,
平行于,平行于,平行于,,
,
,
设,
则,
,
,
,
解得:,
.
15.(1)购买A种水果2千克,B种水果1千克
(2)①;②
本题考查的是一元一次方程的应用,一元一次不等式的应用,二元一次方程组的应用;
(1)设购买A种水果x千克,B种水果y千克,根据在这家商店按标价买了A,B两种水果共3千克,合计付款46元.再建立方程组解题即可;
(2)①设小明买A水果千克,则B种水果购买了千克,根据要求B水果比A水果多买1千克,合计付款不超过50元,再建立不等式求解即可;②设小明买A水果千克,则B种水果购买了千克,根据不同的优惠方式可得,再解方程即可.
(1)解:设购买A种水果x千克,B种水果y千克,
依题意得:,
解得:.
答:购买A种水果2千克,B种水果1千克.
(2)解:①设小明买A水果千克,则B种水果购买了千克,
∴,
解得:,
∴结合实际可得:;
②设小明买A水果千克,则B种水果购买了千克,
∴,
解得:.
16.(1)55
(2)
(3)或
(1)利用勾股定理求解即可;
(2)利用直角三角形斜边中线的性质求得,得到,,推出,,分当点Q在上和点Q在上时,两种情况讨论,分别求得,,据此求解即可;
(3)根据题意求得,分当点Q在上和点Q在上时两种情况讨论,列式一元一次方程方程,求解即可.
(1)解:∵,,
∴,
∵D为中点,
∴,
∵,
∴机器人乙运动的路线长为,
故答案为:55;
(2)解:根据题意,得,
∵中,,为中点,
∴,
∴,,
∴,,
当点Q在上时,,
∴,解得,
当点Q在上时,作,垂足为H(如图),
则.
∵,
∴,
∴,
∴,
解得,
∴;
(3)解:当时,,
此时,,
∴,
∴,
∴,
当点Q在上时,由,得,
解得.
当点Q在上时,由,得,
解得.
∴或.
本题考查了解直角三角形的应用,勾股定理,一元一次方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件.
17.(1)第一次实验用粮食糟醅和芋头糟醅的质量分别是40、20公斤.
(2)需要准备公斤大米.
本题主要考查了二元一次方程组、一元一次方程的应用等知识点,审清题意、正确列出方程组和方程是解题的关键.
(1)第一次实验用粮食糟醅和芋头糟醅的质量分别是x、y公斤,则第一次实验用粮食糟醅和芋头糟醅的质量分别是公斤,然后根据题意列二元一次方程组求解即可;
(2)先求出两次得到粮食酒的总质量,设需要准备z公斤大米,则粮食糟醅的质量为,再根据题意列一元一次方程求解即可.
(1)解:第一次实验用粮食糟醅和芋头糟醅的质量分别是x、y公斤,则第一次实验用粮食糟醅和芋头糟醅的质量分别是公斤,
由题意可得:,解得:.
答:第一次实验用粮食糟醅和芋头糟醅的质量分别是40、20公斤.
(2)解:两次实验得到的粮食酒总量为公斤,
设需要准备z公斤大米,则粮食糟醅的质量为,
由题意可得:,解得:千克.
答:需要准备公斤大米.
18.(1)(2)
本题考查实数的运算,解一元一次方程,熟练掌握相关运算法则,解一元一次方程的步骤,是解题的关键:
(1)先开方,去绝对值,再进行加减运算即可;
(2)去括号,移项,合并,系数化1,进行计算即可.
解:(1)原式;
(2)去括号,得:,
移项,得:,
合并,得:.
19.(1)
(2)注水5小时可供发电万千瓦时.
本题考查一次函数的应用、一元一次方程的应用等知识点,正确列出函数解析式和方程是解题的关键.
(1)根据蓄水池的水位高度等于注水时水位每小时升高的高度乘以注水时间与本次注水前蓄水池的水位高度的和,据此列出函数关系式即可;
(2)根据y与x的函数关系式以及已知条件列关于x的一元一次方程并求解即可.
(1)解:由题意可得:蓄水池的水位高度y(米)与注水时间x(小时)之间的关系式.
(2)解:根据题意,得,
解得.
答:注水5小时可供发电万千瓦时.
20.(1)的值为;
(2)当时,;当时,.
本题考查了分式求值,等式的性质,函数求值,掌握知识点的应用是解题的关键.
()把,代入函数即可求解;
()将,代入函数整理得,然后分当时,即和当时两种情况求解即可.
(1)解:把,代入函数得,
,
∴的值为;
(2)解:将,代入函数得,
,
整理得:,
当时,即,
∴,
当时,,
则有,,
,
∴
,
综上可知:当时,;当时,.
21.(1)该厂每天生产的甲文创产品数量为个,乙文创产品数量是个
(2)每天乙文创产品增加的数量是个
本题考查一元一次方程和分式方程的应用,正确理解题意,根据等量关系列方程是解题的关键.
(1)设该厂每天生产的乙文创产品数量是x个,根据题意列一元一次方程解答即可;
(2)设该厂每天乙文创产品增加的数量是个,根据“生产甲、乙两种文创产品各1400个,乙比甲多用10天”列分式方程解答即可.
(1)解:设该厂每天生产的乙文创产品数量是x个,则甲文创产品数量为个.
,
解得:,
则甲文创产品数量为个,
答:该厂每天生产的乙文创产品数量是个,则甲文创产品数量为个.
(2)解:设每天乙文创产品增加的数量是个,则甲文创产品增加的数量是个.
,
解得:,
经检验:是原方程的解,
答:每天乙文创产品增加的数量是个.
同课章节目录
