专题11平面直角坐标系与函数基础知识(含答案+解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用)
文档属性
| 名称 | 专题11平面直角坐标系与函数基础知识(含答案+解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 15:55:23 | ||
图片预览




文档简介
专题11 平面直角坐标系与函数基础知识(27题)
一、单选题
1.(2025·广西·中考真题)如图,在平面直角坐标系中,“双曲线阶梯”的所有线段均与轴平行或垂直,且满足,点,,,均在双曲线的一支上.若点A的坐标为,则第三级阶梯的高( )
A. B. C. D.
2.(2025·河北·中考真题)若一元二次方程的两根之和与两根之积分别为,,则点在平面直角坐标系中位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2025·山东威海·中考真题)某广场计划用如图①所示的A,B两种瓷砖铺成如图②所示的图案.第一行第一列瓷砖的位置记为,其右边瓷砖的位置记为,其上面瓷砖的位置记为,按照这样的规律,下列说法正确的是( )
A.位置是B种瓷砖 B.位置是B种瓷砖
C.位置是A种瓷砖 D.位置是B种瓷砖
4.(2025·四川内江·中考真题)对于正整数x,规定函数.在平面直角坐标系中,将点中的,分别按照上述规定,同步进行运算得到新的点的横、纵坐标(其中,均为正整数).例如,点经过第次运算得到点.经过第次运算得到点,经过第次运算得到点,经过有限次运算后,必进入循环圈,按上述规定,将点经过第次运算后得到点是( )
A. B. C. D.
5.(2025·四川成都·中考真题)在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2025·四川自贡·中考真题)如图,在平面直角坐标系中,正方形的边长为5,边在轴上..若将正方形绕点逆时针旋转.得到正方形.则点的坐标为( )
A. B.
C. D.
7.(2025·广西·中考真题)生态学家G.F.Gause通过多次单独培养大草履虫实验,研究其种群数量随时间的变化情况,得到了如图所示的“S”形曲线.下列说法正确的是( )
A.第5天的种群数量为300个 B.前3天种群数量持续增长
C.第3天的种群数量达到最大 D.每天增加的种群数量相同
8.(2025·黑龙江齐齐哈尔·中考真题)如图,在菱形中,,,动点从点出发沿边匀速运动,运动到点时停止,过点作的垂线,在点运动过程中,垂线扫过菱形(即阴影部分)的面积为,点运动的路程为.下列图象能反映与之间函数关系的是( )
B.C.D.
9.(2025·甘肃平凉·中考真题)如图1,在等腰直角三角形中,,点D为边的中点;动点P从点A出发,沿边方向匀速运动,运动到点B时停止.设点P的运动路程为x,的面积为y,y与x的函数图象如图2所示,当点P运动到的中点时,的长为( )
A.2 B.2.5 C. D.4
10.(2025·浙江·中考真题)为了实时规划路径,卫星导航系统需要计算运动点与观测点之间距离的平方.如图1,点P是一个固定观测点,运动点Q从A处出发,沿笔直公路向目的地B处运动.设为x(单位:)为y(单位:).如图2,y关于x的函数图象与y轴交于点C,最低点,且经过和两点.下列选项正确的是( )
A. B.
C.点C的纵坐标为240 D.点在该函数图象上
11.(2025·山西·中考真题)氢气是一种绿色清洁能源,可通过电解水获得.实践小组通过实验发现,在电解水的过程中,生成物氢气的质量与分解的水的质量满足我们学过的某种函数关系.下表是一组实验数据,根据表中数据,与之间的函数关系式为( )
水的质量
氢气的质量
A. B. C. D.
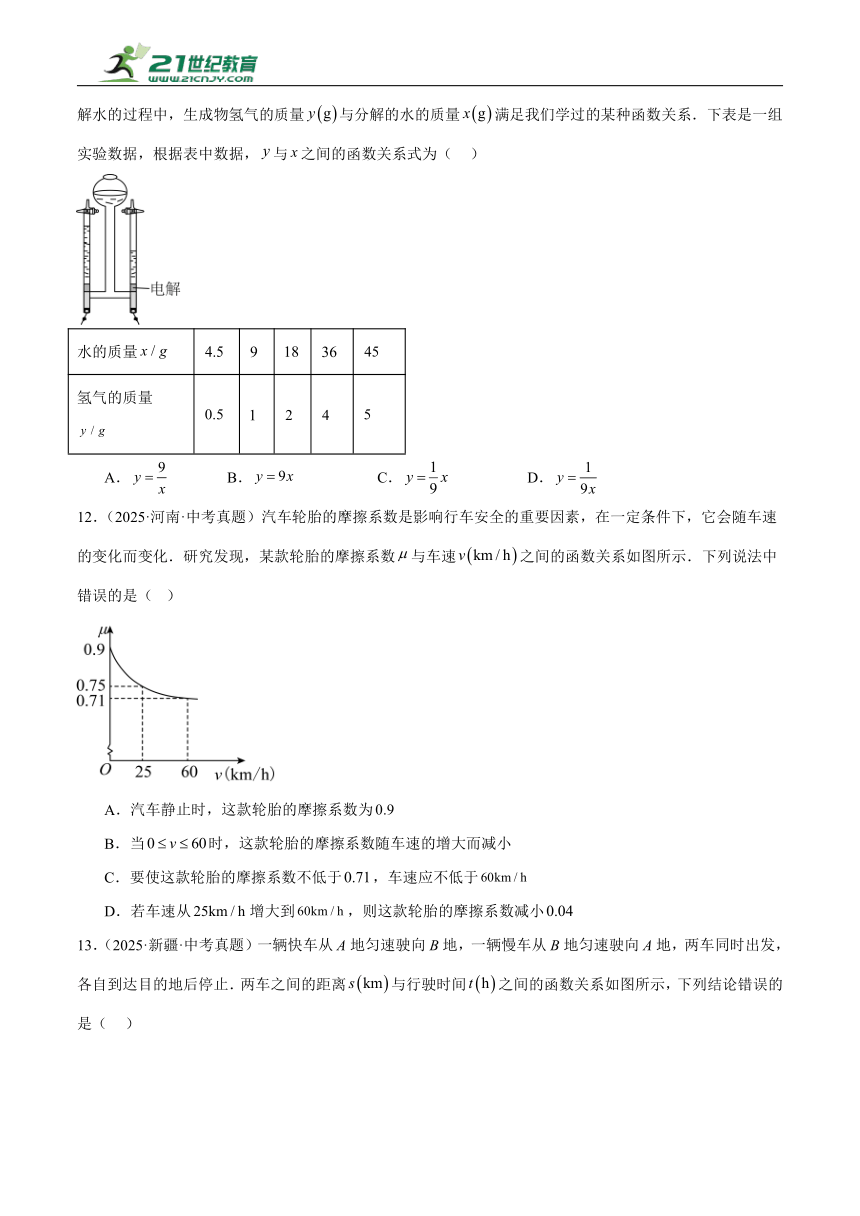
12.(2025·河南·中考真题)汽车轮胎的摩擦系数是影响行车安全的重要因素,在一定条件下,它会随车速的变化而变化.研究发现,某款轮胎的摩擦系数与车速之间的函数关系如图所示.下列说法中错误的是( )
A.汽车静止时,这款轮胎的摩擦系数为
B.当时,这款轮胎的摩擦系数随车速的增大而减小
C.要使这款轮胎的摩擦系数不低于,车速应不低于
D.若车速从增大到,则这款轮胎的摩擦系数减小
13.(2025·新疆·中考真题)一辆快车从A地匀速驶向B地,一辆慢车从B地匀速驶向A地,两车同时出发,各自到达目的地后停止.两车之间的距离与行驶时间之间的函数关系如图所示,下列结论错误的是( )
A.两车出发后相遇
B.A,B两地相距
C.快车比慢车早到达目的地
D.快车的速度为,慢车的速度为
14.(2025·甘肃·中考真题)如图1,在等腰直角三角形中,,点D为边的中点.动点P从点A出发,沿边方向匀速运动,运动到点B时停止.设点P的运动路程为x,的面积为y,y与x的函数图象如图2所示,当点P运动到的中点时,的长为( )
A.2 B.2.5 C. D.4
15.(2025·山东·中考真题)在水分、养料等条件一定的情况下,某植物的生长速度(厘米/天)和光照强度(勒克斯)之间存在一定关系.在低光照强度范围()内,与近似成一次函数关系;在中高光照强度范围内,与近似成二次函数关系.其部分图象如图所示.根据图象,下列结论正确的是( )
A.当时,随的增大而减小 B.当时,有最大值
C.当时, D.当时,
16.(2025·四川成都·中考真题)小明从家跑步到体育馆,在那里锻炼了一段时间后又跑步到书店买书,然后步行回家(小明家、书店、体育馆依次在同一直线上),如图表示的是小明离家的距离与时间的关系.下列说法正确的是( )
A.小明家到体育馆的距离为 B.小明在体育馆锻炼的时间为
C.小明家到书店的距离为 D.小明从书店到家步行的时间为
二、填空题
17.(2025·四川泸州·中考真题)若点在第一象限,则的取值范围是 .
18.(2025·四川德阳·中考真题)在平面直角坐标系中,已知,,如果的面积为,那么点的坐标可以是 .(只需写出一个即可)
19.(2025·四川眉山·中考真题)如图,在平面直角坐标系中,用12个以点O为公共顶点的相似三角形组成形如海螺的图案,若,,则点G的坐标为
20.(2025·山东·中考真题)取直线上一点,①过点作轴的垂线,交于点;②过点作轴的垂线,交于点;如此循环进行下去.按照上面的操作,若点的坐标为,则点的坐标是 .
21.(2025·四川广安·中考真题)在平面直角坐标系中,已知点A的坐标为,且a,b满足,则点A在第 象限.
22.(2025·湖南·中考真题)甲、乙两人在一次100米赛跑比赛中,路程(米)与时间(秒)的函数关系如图所示,填 (“甲”或“乙”)先到终点:
23.(2025·湖北·中考真题)如图1,在中,.动点P,Q均以的速度从点同时出发,点沿折线向点运动,点沿边CA向点运动.当点运动到点时,两点都停止运动.的面积(单位:)与运动时间(单位:s)的关系如图2所示.(1) ;(2) .
三、解答题
24.(2025·广西·中考真题)绣球是广西民族文化的特色载体.如图,设计某种绣球叶瓣时,可以先在图纸上建立平面直角坐标系,再分别以原点,为圆心、以为半径作圆,两圆相交于两点,其公共部分构成叶瓣①(阴影部分),同理得到叶瓣②.
(1)写出两点的坐标;
(2)求叶瓣①的周长;(结果保留)
(3)请描述叶瓣②还可以由叶瓣①经过怎样的图形变化得到.
25.(2025·安徽·中考真题)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,的顶点和均为格点(网格线的交点).已知点A和的坐标分别为和.
(1)在所给的网格图中描出边的中点D,并写出点D的坐标;
(2)以点O为位似中心,将放大得到,使得点A的对应点为,请在所给的网格图中画出.
26.(2025·重庆·中考真题)如图,点为矩形的对角线AC的中点,,,,是上的点(,均不与,重合),且,连接,.用表示线段的长度,点与点的距离为.矩形的面积为,的面积为,的面积为,.
(1)请直接写出,分别关于的函数表达式,并写出自变量的取值范围:
(2)在给定的平面直角坐标系中画出函数,的图象,并分别写出函数,的一条性质;
(3)结合函数图象,请直接写出时的取值范围(近似值保留小数点后一位,误差不超过).
27.(2025·黑龙江齐齐哈尔·中考真题)2025年春晚舞台上的机器人表演,充分演绎了科技与民族文化的完美融合.为满足学生的好奇心和求知欲,某校组织科技活动“机器人走进校园”,AI热情瞬间燃爆.校园里一条笔直的“勤学路”上依次设置了A,B,C三个互动区,机器人甲、乙分别从A,C两区同时出发开始表演,机器人甲沿“勤学路”以20米/分的速度匀速向B区行进,行至B区时停留4.5分钟(与师生热情互动)后,继续沿“勤学路”向C区匀速行进,机器人乙沿“勤学路”以10米/分的速度匀速向B区行进,行至B区时接到指令立即匀速返回,结果两机器人同时到达C区.机器人甲、乙距B区的距离y(米)与机器人乙行进的时间x(分)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)A,C两区相距__________米,__________;
(2)求线段所在直线的函数解析式;
(3)机器人乙行进的时间为多少分时,机器人甲、乙相距30米?(直接写出答案即可)
《专题11 平面直角坐标系与函数基础知识-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B A B A B A A D
题号 11 12 13 14 15 16
答案 C C C A B C
1.B
本题考查了双曲线的解析式,点的坐标与线段长度,解题的关键是得出双曲线的解析式.
把点的坐标代入,可得双曲线的解析式,结合已知的线段长度求出点和点的横坐标,代入解析式可得纵坐标,作差即可.
解:∵点在双曲线上,
∴,
∴双曲线,
∵“双曲线阶梯”的所有线段均与轴平行或垂直,且,
∴点的横坐标为,点的横坐标为,
∴点的纵坐标为,点的纵坐标为,
∴,
故选:.
2.C
本题考查了一元二次方程根与系数的关系,点的坐标;将方程化为标准形式后,利用根与系数的关系求出两根之和与积,再根据点的坐标判断所在象限.
解:原方程 展开并整理为标准形式:
其中 ,,.
∴,.
∴点即 的横、纵坐标均为负数,故位于平面直角坐标系的第三象限.
故选:C.
3.B
本题考查了点的坐标规律探索,找到规律是关键;
根据题意可得:A种瓷砖的坐标规律为(单数,双数),(双数,单数);B种瓷砖的坐标规律为(单数,单数),(双数,双数),再逐项判断即可.
解:A种瓷砖的位置:,
,
B种瓷砖的位置:,
,
由此可得:A种瓷砖的坐标规律为(单数,双数),(双数,单数);B种瓷砖的坐标规律为(单数,单数),(双数,双数);
∴位置是A种瓷砖,故A选项不符合题意;
位置是B种瓷砖,故B选项符合题意;
位置是B种瓷砖,故C选项不符合题意;
位置是A种瓷砖,故D选项不符合题意;
故选:B.
4.A
本题考查了数字类规律探究,点的坐标规律,求函数值,通过计算点每次运算后的结果,发现其变化呈现周期性循环,周期为3次.利用周期性规律,确定第2025次运算后的结果.
解:初始点:(第0次运算).
第1次: 横坐标为偶数,; 纵坐标为奇数,; 得到点.
第2次: 横坐标为奇数,; 纵坐标为偶数,; 得到点.
第3次: 横坐标为偶数,; 纵坐标为偶数,; 得到点,与初始点相同,
即三次一循环,
,
∴第次运算后对应点与第3次运算后的点相同,即.
故选:A.
5.B
本题考查判断点所在的象限,根据点的符号特点,判断点所在的象限即可,熟练掌握各象限的点的符号特点,是解题的关键.
解:∵,,,
∴点在第二象限;
故选B.
6.A
本题考查的是正方形的性质,旋转的性质,坐标与图形,由正方形与旋转可得在轴上,,结合,可得,,进一步可得答案.
解:∵正方形的边长为5,边在轴上,将正方形绕点逆时针旋转.得到正方形.
∴,在轴上,,
∵,
∴,,
∴,
故选:A
7.B
本题考查了从函数图象获取相关信息,认真读题,分析每个阶段的函数图象是解题的关键.根据图像,逐项分析即可得出结论.
解:A. 第5天的种群数量在之间,选项说法错误,故不符合题意;
B. 前3天种群数量持续增长,选项说法正确,故符合题意;
C. 第5天的种群数量达到最大,选项说法错误,故不符合题意;
D. 由图可得,每天增加的种群数量不相同,选项说法错误,故不符合题意;
故选:B.
8.A
分三种情况:点E在上时,点E在上且l与相交时,点E在上且l与相交时,分别计算出阴影部分面积的表达式,即可求解.
解:当点E在上时,如图,
,,
,
,,
,
此时图象为开口上的抛物线的一部分,排除C,D选项;
当点E在上且l与相交时,作,如图,
,,
,
,,
,
此时图象为直线一部分;
当点E在上且l与相交时,如图,
,,,
,
,
,
此时图象为开口下的抛物线的一部分,排除B选项;
故选A.
本题考查菱形上的动点问题,解直角三角形,勾股定理,二次函数的图象和性质,一次函数的图象和性质等,求出不同阶段y与x的解析式是解题的关键.
9.A
本题考查了根据函数图象得到信息,三角形中位线,等腰直角三角形的性质,得到当点P运动到点C时,的面积最大是解题的关键;
根据运动轨迹可得的面积先增大再减小,可得当点P运动到点C时,的面积最大为4,即可求得,再利用三角形中位线定理即可解答.
解:根据题意动点P从点A出发,沿边方向匀速运动过程中,的面积先增大再减小,当点P运动到点C时,的面积最大,根据函数图象可得此时的面积为4,如图,
∵等腰直角三角形,,点D为边的中点,
∴,
∴,
当点P运动到的中点时,
∵点D为边的中点,
∴;
故选:A.
10.D
作,当时,动点运动到点的位置,得到,当点运动到点的时候,最小为,,勾股定理求出的值,判断A;当时,点运动到点,根据三线合一,得到,进而求出的值,判断B;连接,勾股定理求出的长,确定的纵坐标,判断C,求出时,点的位置,再利用勾股定理求出,判断D,即可.
解:如图,作,当时,动点运动到点的位置,则由题意和图象可知,当点运动到点的时候,最小,即:,,
在中,由勾股定理,得:,
解得:,故选项A错误;
∴,,
当时,点运动到点,则,
∴,
∵,
∴,
∴,故选项B错误;
∴当,即点在点时,
∴;
∴点的纵坐标为;故选项C错误;
当时,点运动到点,则:,
∴,
∴,
∴点在该函数图象上,故选项D正确;
故选D.
本题考查动点的函数图象,勾股定理,垂线段最短,三线合一等知识点,熟练掌握相关知识点,从函数图象中有效的获取信息,确定点的位置,是解题的关键.
11.C
本题考查了求函数关系式,由表格数据可得是的正比例函数,进而即可求解,由表格数据判断出函数关系是解题的关键.
解:∵,
∴与成正比例,即是的正比例函数,
∴,
故选:.
12.C
本题考查了利用函数图象获取信息,正确理解函数图象是解题关键.根据某款轮胎的摩擦系数与车速之间的函数关系图,逐项判断即可.
解:A、由图象可知,当时,,即汽车静止时,这款轮胎的摩擦系数为,原说法正确,不符合题意;
B、由图象可知,当时,这款轮胎的摩擦系数随车速的增大而减小,原说法正确,不符合题意;
C、要使这款轮胎的摩擦系数不低于,车速应不高于,原说法错误,符合题意;
D、由图象可知,当时,;当时,,即车速从增大到,则这款轮胎的摩擦系数减小,原说法正确,不符合题意;
故选:C
13.C
本题主要考查了从函数图象获取信息,根据时,,时,可判断A、B;根据函数图象可得快车出发到达目的地,慢车出发到达目的地,据此根据速度等于路程除以时间求出两车的速度,即可判断C、D.
解:∵时,,
∴A,B两地相距,故B结论正确,不符合题意;
∵时,,
∴两车出发后相遇,故A结论正确,不符合题意;
由函数图象可得快车出发到达目的地,慢车出发到达目的地,
∴快车比慢车早到达目的地,故C结论错误,符合题意;
,,
∴快车的速度为,慢车的速度为,故D结论正确,不符合题意;
故选:C.
14.A
本题考查了根据函数图象得到信息,三角形中位线,等腰直角三角形,根据运动轨迹可得的面积先增大,再减小,当点P运动到点时,的面积最大,此时的面积为,即可求得,再利用三角形中位线定理即可解答,得到当点P运动到点时,的面积最大是解题的关键.
解:根据题意动点P从点A出发,沿边方向匀速运动过程中,
的面积先增大,再减小,
当点P运动到点时,的面积最大,
根据函数图象可得此时的面积为,
如图,
,点D为边的中点,等腰直角三角形,
,
可得,
当点P运动到的中点时,如图,
,点D为边的中点,
,
故选:A.
15.B
本题主要考查了二次函数图象的性质、二次函数与不等式等知识点,掌握数形结合思想是解题的关键.
根据抛物线可直接判断A选项;根据抛物线以及相关数据可得抛物线的对称轴为,进而判定B选项;根据函数图象可判定C选项;根据二次函数的对称性可判定D选项.
解:A.当时,随的增大先增大、后减小,即A选项错误,不符合题意;
B.由函数图象可知:抛物线的对称轴为,即当时,有最大值,则B选项正确,符合题意;
C.由函数图象可知:当时,,即C选项错误,不符合题意;
D.当时,由图象知,对应的值有两个,即D选项错误,不符合题意.
故选B.
16.C
本题考查用函数图象表示变量之间的关系,从函数图象中有效的获取信息,逐一进行判断即可.
解:由图象可知:小明家到体育馆的距离为;故选项A错误;
小明在体育馆锻炼的时间为;故选项B错误;
小明家到书店的距离为;故选项C正确;
小明从书店到家步行的时间为;故选项D错误;
故选C.
17.
本题考查象限内点的符号特征,解一元一次不等式.解题的关键是掌握坐标系中每个象限内点的符号特点如下:第一象限,第二象限,第三象限,第四象限.
根据第一象限内点的坐标符号为,得到,再解一元一次不等式即可.
解:∵点在第一象限,
∴,
解得:,
故答案为:.
18.(答案不唯一,纵坐标绝对值为即可)
本题考查了平面直角坐标系中点的位置,三角形面积公式,由,,得,又的面积为,可得,所以,从而求解,掌握知识点的应用是解题的关键.
解:∵,,
∴,
∵的面积为,
∴,
∴,
∴,
∴点的坐标可以是,
故答案为:.(答案不唯一,纵坐标绝对值为即可)
19.
本题考查了相似三角形的性质、解直角三角形和点的坐标规律探求;先求得,然后解直角三角形分别求出,,,得到规律,再根据规律计算即可.
解:∵图案是用12个以点O为公共顶点的相似三角形组成形如海螺的图案,
∴,
∵,,
∴,
∵,
∴,
同理:,
依次类推:;
则点G的坐标为;
故答案为:.
20.
本题考查了一次函数和反比例函数规律探究;根据题意可以写出点、、、的坐标,从而可以发现各点的变化规律,从而可以写出点的坐标.
解:∵点的坐标为,
∴点的横坐标为1,
∴点的坐标为,
∴点的纵坐标为1,
∴点的坐标为,
同理点的横坐标为,
∴点的坐标为,
点的坐标为,
∴四个点一个循环,
∵余1,
∴点的坐标与点相同,是,
故答案为:.
本题考查一次函数图象上点的坐标特征、规律型,勾股定理,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
21.四
本题考查非负性,判断点所在的象限,根据非负性求出的值,根据的符号,判断出点A所在的象限即可.
解:∵,
∴,
∴,
∴点A的坐标为,在第四象限;
故答案为:四.
22.甲
本题考查函数图象的应用,解题的关键是明确题意,利用数形结合的思想解答问题.
从函数图象可知甲乙跑完全程的时间,即可确定答案.
解:根据图象可得甲到达终点用时秒,乙到达终点用时秒,
∴甲先到达终点,
故答案为:甲.
23. 8 12
本题考查动点的函数图象,相似三角形的判定和性质,从函数图象中有效的获取信息,是解题的关键:
(1)观察图象可知,当时,点与点重合,得到,利用直角三角形的面积公式进行计算,求出的值即可;
(2)根据图象当时,,此时,过点作,根据面积公式求出的长,证明,列出比例式求出的长,进而求出的长即可.
解:(1)观察图象可知,当时,点与点重合,
∵动点P,Q均以的速度从点同时出发,
∴,
∵,
∴;
故答案为:;
(2)由图象可知,当时,,此时,
过点作于点,如图:则:,
∵,
∴,
∵,
∴,
∴,
∴,
∴为的中点,
∴;
故答案为:12.
24.(1)
(2)
(3)叶瓣②还可以由叶瓣①逆时针旋转得到
本题考查了圆的性质、平面直角坐标系、旋转:
(1)先证明四边形是正方形即可得到坐标;
(2)根据,算出圆的周长即可得到叶瓣的周长;
(3)利用旋转即可.
(1)以原点,为圆心、以为半径作圆,两圆相交于两点
是正方形
(2)原点,为圆心、以为半径作圆
两个圆是等圆
叶瓣①的周长为:
(3)叶瓣②还可以由叶瓣①逆时针旋转得到.
25.(1)图见解析;
(2)图见解析
本题主要考查了中点坐标公式,坐标系中画位似图形,熟知中点坐标公式,位似图形的性质是解题的关键.
(1)根据两点中点坐标公式可确定点D的坐标,进而描出点D即可;
(2)根据点A和点的坐标可知,把B、C的横纵坐标都乘以即可得到的坐标,描出,并顺次连接即可.
(1)解:如图所示,点D即为边的中点,
∵,
∴点D的坐标为.
(2)解:如图所示,即为所求作的三角形.
26.(1),
(2)作图见解析,性质:当时,随的增大而减小,当时,随的增大而增大(不唯一);当时,随的增大而减小
(3)(或或或或)
本题考查函数解析式,一次函数的图象与性质,反比例函数的图象与性质,反比例函数与不等式,勾股定理,矩形的性质,熟练掌握相关性质,并能正确分段列出动点问题的相关线段是解题的关键.
(1)利用矩形性质和勾股定理得出,,分两部分:①当时;②当时,分别列出;过点作于点,利用等面积法求出,即可表示出的面积为,同理可得的面积为,再结合矩形的面积为与,即可列出;
(2)根据函数解析式画图即可,再根据函数图象写出性质;
(3)根据图象写出的图象在下方时对应的自变量的取值范围即可
(1)解:∵为矩形的对角线AC的中点,,,
∴,,
∴,
当时,,如图,
∴;
当时,,如图,
∴;
∴;
如图,过点作于点,
∵,
∴,
∴的面积为,
同理可得的面积为,
又∵矩形的面积为,
∴,
∴;
(2)解:作图如下:
性质:当时,随的增大而减小;当时,随的增大而增大(不唯一);当时,随的增大而减小;
(3)解:结合函数图象,可得时的取值范围为(或<或或或).
27.(1)
(2)
(3)7分或11分或13分
本题主要考查一次函数的应用和从函数图象获取信息,熟练掌握一次函数的应用是解题的关键.
(1)根据图象可直接进行求解A、C两区之间的距离,然后再结合甲的行进情况可求解a;
(2)求出,由图象可得,设直线的解析式为,进而问题可求解;
(3)由题意可分三种情况分别进行求解即可.
(1)解:由题意可得,A,C两区相距为(米),
由题意可知,表示甲到达B区的时间,则,
故答案为:
(2)由题意可知,点E表示机器人乙沿“勤学路”以10米/分的速度匀速到达了B区,
∴点E的横坐标为,
∴,
设直线的解析式为,把,代入得到,
,解得:,
∴线段所在直线的函数解析式为:;
(3)机器人乙行进的时间为x分时,甲和乙都未到达B区,相距30米,
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
机器人乙行进的时间为t分时,从B点返回,且甲仍在B区停留期间,相距30米,
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
机器人乙行进的时间为n分时,从B点返回途中,且甲离开B区向C区前进时,相距30米,
当时,甲机器人距B区的距离y(米)与机器人乙行进的时间x(分)之间的函数关系为,把,代入得到,
,解得:,
∴线段所在直线的函数解析式为:;
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
综上可知,机器人乙行进的时间7分或11分或13分时,机器人甲、乙相距30米.
一、单选题
1.(2025·广西·中考真题)如图,在平面直角坐标系中,“双曲线阶梯”的所有线段均与轴平行或垂直,且满足,点,,,均在双曲线的一支上.若点A的坐标为,则第三级阶梯的高( )
A. B. C. D.
2.(2025·河北·中考真题)若一元二次方程的两根之和与两根之积分别为,,则点在平面直角坐标系中位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2025·山东威海·中考真题)某广场计划用如图①所示的A,B两种瓷砖铺成如图②所示的图案.第一行第一列瓷砖的位置记为,其右边瓷砖的位置记为,其上面瓷砖的位置记为,按照这样的规律,下列说法正确的是( )
A.位置是B种瓷砖 B.位置是B种瓷砖
C.位置是A种瓷砖 D.位置是B种瓷砖
4.(2025·四川内江·中考真题)对于正整数x,规定函数.在平面直角坐标系中,将点中的,分别按照上述规定,同步进行运算得到新的点的横、纵坐标(其中,均为正整数).例如,点经过第次运算得到点.经过第次运算得到点,经过第次运算得到点,经过有限次运算后,必进入循环圈,按上述规定,将点经过第次运算后得到点是( )
A. B. C. D.
5.(2025·四川成都·中考真题)在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2025·四川自贡·中考真题)如图,在平面直角坐标系中,正方形的边长为5,边在轴上..若将正方形绕点逆时针旋转.得到正方形.则点的坐标为( )
A. B.
C. D.
7.(2025·广西·中考真题)生态学家G.F.Gause通过多次单独培养大草履虫实验,研究其种群数量随时间的变化情况,得到了如图所示的“S”形曲线.下列说法正确的是( )
A.第5天的种群数量为300个 B.前3天种群数量持续增长
C.第3天的种群数量达到最大 D.每天增加的种群数量相同
8.(2025·黑龙江齐齐哈尔·中考真题)如图,在菱形中,,,动点从点出发沿边匀速运动,运动到点时停止,过点作的垂线,在点运动过程中,垂线扫过菱形(即阴影部分)的面积为,点运动的路程为.下列图象能反映与之间函数关系的是( )
B.C.D.
9.(2025·甘肃平凉·中考真题)如图1,在等腰直角三角形中,,点D为边的中点;动点P从点A出发,沿边方向匀速运动,运动到点B时停止.设点P的运动路程为x,的面积为y,y与x的函数图象如图2所示,当点P运动到的中点时,的长为( )
A.2 B.2.5 C. D.4
10.(2025·浙江·中考真题)为了实时规划路径,卫星导航系统需要计算运动点与观测点之间距离的平方.如图1,点P是一个固定观测点,运动点Q从A处出发,沿笔直公路向目的地B处运动.设为x(单位:)为y(单位:).如图2,y关于x的函数图象与y轴交于点C,最低点,且经过和两点.下列选项正确的是( )
A. B.
C.点C的纵坐标为240 D.点在该函数图象上
11.(2025·山西·中考真题)氢气是一种绿色清洁能源,可通过电解水获得.实践小组通过实验发现,在电解水的过程中,生成物氢气的质量与分解的水的质量满足我们学过的某种函数关系.下表是一组实验数据,根据表中数据,与之间的函数关系式为( )
水的质量
氢气的质量
A. B. C. D.
12.(2025·河南·中考真题)汽车轮胎的摩擦系数是影响行车安全的重要因素,在一定条件下,它会随车速的变化而变化.研究发现,某款轮胎的摩擦系数与车速之间的函数关系如图所示.下列说法中错误的是( )
A.汽车静止时,这款轮胎的摩擦系数为
B.当时,这款轮胎的摩擦系数随车速的增大而减小
C.要使这款轮胎的摩擦系数不低于,车速应不低于
D.若车速从增大到,则这款轮胎的摩擦系数减小
13.(2025·新疆·中考真题)一辆快车从A地匀速驶向B地,一辆慢车从B地匀速驶向A地,两车同时出发,各自到达目的地后停止.两车之间的距离与行驶时间之间的函数关系如图所示,下列结论错误的是( )
A.两车出发后相遇
B.A,B两地相距
C.快车比慢车早到达目的地
D.快车的速度为,慢车的速度为
14.(2025·甘肃·中考真题)如图1,在等腰直角三角形中,,点D为边的中点.动点P从点A出发,沿边方向匀速运动,运动到点B时停止.设点P的运动路程为x,的面积为y,y与x的函数图象如图2所示,当点P运动到的中点时,的长为( )
A.2 B.2.5 C. D.4
15.(2025·山东·中考真题)在水分、养料等条件一定的情况下,某植物的生长速度(厘米/天)和光照强度(勒克斯)之间存在一定关系.在低光照强度范围()内,与近似成一次函数关系;在中高光照强度范围内,与近似成二次函数关系.其部分图象如图所示.根据图象,下列结论正确的是( )
A.当时,随的增大而减小 B.当时,有最大值
C.当时, D.当时,
16.(2025·四川成都·中考真题)小明从家跑步到体育馆,在那里锻炼了一段时间后又跑步到书店买书,然后步行回家(小明家、书店、体育馆依次在同一直线上),如图表示的是小明离家的距离与时间的关系.下列说法正确的是( )
A.小明家到体育馆的距离为 B.小明在体育馆锻炼的时间为
C.小明家到书店的距离为 D.小明从书店到家步行的时间为
二、填空题
17.(2025·四川泸州·中考真题)若点在第一象限,则的取值范围是 .
18.(2025·四川德阳·中考真题)在平面直角坐标系中,已知,,如果的面积为,那么点的坐标可以是 .(只需写出一个即可)
19.(2025·四川眉山·中考真题)如图,在平面直角坐标系中,用12个以点O为公共顶点的相似三角形组成形如海螺的图案,若,,则点G的坐标为
20.(2025·山东·中考真题)取直线上一点,①过点作轴的垂线,交于点;②过点作轴的垂线,交于点;如此循环进行下去.按照上面的操作,若点的坐标为,则点的坐标是 .
21.(2025·四川广安·中考真题)在平面直角坐标系中,已知点A的坐标为,且a,b满足,则点A在第 象限.
22.(2025·湖南·中考真题)甲、乙两人在一次100米赛跑比赛中,路程(米)与时间(秒)的函数关系如图所示,填 (“甲”或“乙”)先到终点:
23.(2025·湖北·中考真题)如图1,在中,.动点P,Q均以的速度从点同时出发,点沿折线向点运动,点沿边CA向点运动.当点运动到点时,两点都停止运动.的面积(单位:)与运动时间(单位:s)的关系如图2所示.(1) ;(2) .
三、解答题
24.(2025·广西·中考真题)绣球是广西民族文化的特色载体.如图,设计某种绣球叶瓣时,可以先在图纸上建立平面直角坐标系,再分别以原点,为圆心、以为半径作圆,两圆相交于两点,其公共部分构成叶瓣①(阴影部分),同理得到叶瓣②.
(1)写出两点的坐标;
(2)求叶瓣①的周长;(结果保留)
(3)请描述叶瓣②还可以由叶瓣①经过怎样的图形变化得到.
25.(2025·安徽·中考真题)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,的顶点和均为格点(网格线的交点).已知点A和的坐标分别为和.
(1)在所给的网格图中描出边的中点D,并写出点D的坐标;
(2)以点O为位似中心,将放大得到,使得点A的对应点为,请在所给的网格图中画出.
26.(2025·重庆·中考真题)如图,点为矩形的对角线AC的中点,,,,是上的点(,均不与,重合),且,连接,.用表示线段的长度,点与点的距离为.矩形的面积为,的面积为,的面积为,.
(1)请直接写出,分别关于的函数表达式,并写出自变量的取值范围:
(2)在给定的平面直角坐标系中画出函数,的图象,并分别写出函数,的一条性质;
(3)结合函数图象,请直接写出时的取值范围(近似值保留小数点后一位,误差不超过).
27.(2025·黑龙江齐齐哈尔·中考真题)2025年春晚舞台上的机器人表演,充分演绎了科技与民族文化的完美融合.为满足学生的好奇心和求知欲,某校组织科技活动“机器人走进校园”,AI热情瞬间燃爆.校园里一条笔直的“勤学路”上依次设置了A,B,C三个互动区,机器人甲、乙分别从A,C两区同时出发开始表演,机器人甲沿“勤学路”以20米/分的速度匀速向B区行进,行至B区时停留4.5分钟(与师生热情互动)后,继续沿“勤学路”向C区匀速行进,机器人乙沿“勤学路”以10米/分的速度匀速向B区行进,行至B区时接到指令立即匀速返回,结果两机器人同时到达C区.机器人甲、乙距B区的距离y(米)与机器人乙行进的时间x(分)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)A,C两区相距__________米,__________;
(2)求线段所在直线的函数解析式;
(3)机器人乙行进的时间为多少分时,机器人甲、乙相距30米?(直接写出答案即可)
《专题11 平面直角坐标系与函数基础知识-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B A B A B A A D
题号 11 12 13 14 15 16
答案 C C C A B C
1.B
本题考查了双曲线的解析式,点的坐标与线段长度,解题的关键是得出双曲线的解析式.
把点的坐标代入,可得双曲线的解析式,结合已知的线段长度求出点和点的横坐标,代入解析式可得纵坐标,作差即可.
解:∵点在双曲线上,
∴,
∴双曲线,
∵“双曲线阶梯”的所有线段均与轴平行或垂直,且,
∴点的横坐标为,点的横坐标为,
∴点的纵坐标为,点的纵坐标为,
∴,
故选:.
2.C
本题考查了一元二次方程根与系数的关系,点的坐标;将方程化为标准形式后,利用根与系数的关系求出两根之和与积,再根据点的坐标判断所在象限.
解:原方程 展开并整理为标准形式:
其中 ,,.
∴,.
∴点即 的横、纵坐标均为负数,故位于平面直角坐标系的第三象限.
故选:C.
3.B
本题考查了点的坐标规律探索,找到规律是关键;
根据题意可得:A种瓷砖的坐标规律为(单数,双数),(双数,单数);B种瓷砖的坐标规律为(单数,单数),(双数,双数),再逐项判断即可.
解:A种瓷砖的位置:,
,
B种瓷砖的位置:,
,
由此可得:A种瓷砖的坐标规律为(单数,双数),(双数,单数);B种瓷砖的坐标规律为(单数,单数),(双数,双数);
∴位置是A种瓷砖,故A选项不符合题意;
位置是B种瓷砖,故B选项符合题意;
位置是B种瓷砖,故C选项不符合题意;
位置是A种瓷砖,故D选项不符合题意;
故选:B.
4.A
本题考查了数字类规律探究,点的坐标规律,求函数值,通过计算点每次运算后的结果,发现其变化呈现周期性循环,周期为3次.利用周期性规律,确定第2025次运算后的结果.
解:初始点:(第0次运算).
第1次: 横坐标为偶数,; 纵坐标为奇数,; 得到点.
第2次: 横坐标为奇数,; 纵坐标为偶数,; 得到点.
第3次: 横坐标为偶数,; 纵坐标为偶数,; 得到点,与初始点相同,
即三次一循环,
,
∴第次运算后对应点与第3次运算后的点相同,即.
故选:A.
5.B
本题考查判断点所在的象限,根据点的符号特点,判断点所在的象限即可,熟练掌握各象限的点的符号特点,是解题的关键.
解:∵,,,
∴点在第二象限;
故选B.
6.A
本题考查的是正方形的性质,旋转的性质,坐标与图形,由正方形与旋转可得在轴上,,结合,可得,,进一步可得答案.
解:∵正方形的边长为5,边在轴上,将正方形绕点逆时针旋转.得到正方形.
∴,在轴上,,
∵,
∴,,
∴,
故选:A
7.B
本题考查了从函数图象获取相关信息,认真读题,分析每个阶段的函数图象是解题的关键.根据图像,逐项分析即可得出结论.
解:A. 第5天的种群数量在之间,选项说法错误,故不符合题意;
B. 前3天种群数量持续增长,选项说法正确,故符合题意;
C. 第5天的种群数量达到最大,选项说法错误,故不符合题意;
D. 由图可得,每天增加的种群数量不相同,选项说法错误,故不符合题意;
故选:B.
8.A
分三种情况:点E在上时,点E在上且l与相交时,点E在上且l与相交时,分别计算出阴影部分面积的表达式,即可求解.
解:当点E在上时,如图,
,,
,
,,
,
此时图象为开口上的抛物线的一部分,排除C,D选项;
当点E在上且l与相交时,作,如图,
,,
,
,,
,
此时图象为直线一部分;
当点E在上且l与相交时,如图,
,,,
,
,
,
此时图象为开口下的抛物线的一部分,排除B选项;
故选A.
本题考查菱形上的动点问题,解直角三角形,勾股定理,二次函数的图象和性质,一次函数的图象和性质等,求出不同阶段y与x的解析式是解题的关键.
9.A
本题考查了根据函数图象得到信息,三角形中位线,等腰直角三角形的性质,得到当点P运动到点C时,的面积最大是解题的关键;
根据运动轨迹可得的面积先增大再减小,可得当点P运动到点C时,的面积最大为4,即可求得,再利用三角形中位线定理即可解答.
解:根据题意动点P从点A出发,沿边方向匀速运动过程中,的面积先增大再减小,当点P运动到点C时,的面积最大,根据函数图象可得此时的面积为4,如图,
∵等腰直角三角形,,点D为边的中点,
∴,
∴,
当点P运动到的中点时,
∵点D为边的中点,
∴;
故选:A.
10.D
作,当时,动点运动到点的位置,得到,当点运动到点的时候,最小为,,勾股定理求出的值,判断A;当时,点运动到点,根据三线合一,得到,进而求出的值,判断B;连接,勾股定理求出的长,确定的纵坐标,判断C,求出时,点的位置,再利用勾股定理求出,判断D,即可.
解:如图,作,当时,动点运动到点的位置,则由题意和图象可知,当点运动到点的时候,最小,即:,,
在中,由勾股定理,得:,
解得:,故选项A错误;
∴,,
当时,点运动到点,则,
∴,
∵,
∴,
∴,故选项B错误;
∴当,即点在点时,
∴;
∴点的纵坐标为;故选项C错误;
当时,点运动到点,则:,
∴,
∴,
∴点在该函数图象上,故选项D正确;
故选D.
本题考查动点的函数图象,勾股定理,垂线段最短,三线合一等知识点,熟练掌握相关知识点,从函数图象中有效的获取信息,确定点的位置,是解题的关键.
11.C
本题考查了求函数关系式,由表格数据可得是的正比例函数,进而即可求解,由表格数据判断出函数关系是解题的关键.
解:∵,
∴与成正比例,即是的正比例函数,
∴,
故选:.
12.C
本题考查了利用函数图象获取信息,正确理解函数图象是解题关键.根据某款轮胎的摩擦系数与车速之间的函数关系图,逐项判断即可.
解:A、由图象可知,当时,,即汽车静止时,这款轮胎的摩擦系数为,原说法正确,不符合题意;
B、由图象可知,当时,这款轮胎的摩擦系数随车速的增大而减小,原说法正确,不符合题意;
C、要使这款轮胎的摩擦系数不低于,车速应不高于,原说法错误,符合题意;
D、由图象可知,当时,;当时,,即车速从增大到,则这款轮胎的摩擦系数减小,原说法正确,不符合题意;
故选:C
13.C
本题主要考查了从函数图象获取信息,根据时,,时,可判断A、B;根据函数图象可得快车出发到达目的地,慢车出发到达目的地,据此根据速度等于路程除以时间求出两车的速度,即可判断C、D.
解:∵时,,
∴A,B两地相距,故B结论正确,不符合题意;
∵时,,
∴两车出发后相遇,故A结论正确,不符合题意;
由函数图象可得快车出发到达目的地,慢车出发到达目的地,
∴快车比慢车早到达目的地,故C结论错误,符合题意;
,,
∴快车的速度为,慢车的速度为,故D结论正确,不符合题意;
故选:C.
14.A
本题考查了根据函数图象得到信息,三角形中位线,等腰直角三角形,根据运动轨迹可得的面积先增大,再减小,当点P运动到点时,的面积最大,此时的面积为,即可求得,再利用三角形中位线定理即可解答,得到当点P运动到点时,的面积最大是解题的关键.
解:根据题意动点P从点A出发,沿边方向匀速运动过程中,
的面积先增大,再减小,
当点P运动到点时,的面积最大,
根据函数图象可得此时的面积为,
如图,
,点D为边的中点,等腰直角三角形,
,
可得,
当点P运动到的中点时,如图,
,点D为边的中点,
,
故选:A.
15.B
本题主要考查了二次函数图象的性质、二次函数与不等式等知识点,掌握数形结合思想是解题的关键.
根据抛物线可直接判断A选项;根据抛物线以及相关数据可得抛物线的对称轴为,进而判定B选项;根据函数图象可判定C选项;根据二次函数的对称性可判定D选项.
解:A.当时,随的增大先增大、后减小,即A选项错误,不符合题意;
B.由函数图象可知:抛物线的对称轴为,即当时,有最大值,则B选项正确,符合题意;
C.由函数图象可知:当时,,即C选项错误,不符合题意;
D.当时,由图象知,对应的值有两个,即D选项错误,不符合题意.
故选B.
16.C
本题考查用函数图象表示变量之间的关系,从函数图象中有效的获取信息,逐一进行判断即可.
解:由图象可知:小明家到体育馆的距离为;故选项A错误;
小明在体育馆锻炼的时间为;故选项B错误;
小明家到书店的距离为;故选项C正确;
小明从书店到家步行的时间为;故选项D错误;
故选C.
17.
本题考查象限内点的符号特征,解一元一次不等式.解题的关键是掌握坐标系中每个象限内点的符号特点如下:第一象限,第二象限,第三象限,第四象限.
根据第一象限内点的坐标符号为,得到,再解一元一次不等式即可.
解:∵点在第一象限,
∴,
解得:,
故答案为:.
18.(答案不唯一,纵坐标绝对值为即可)
本题考查了平面直角坐标系中点的位置,三角形面积公式,由,,得,又的面积为,可得,所以,从而求解,掌握知识点的应用是解题的关键.
解:∵,,
∴,
∵的面积为,
∴,
∴,
∴,
∴点的坐标可以是,
故答案为:.(答案不唯一,纵坐标绝对值为即可)
19.
本题考查了相似三角形的性质、解直角三角形和点的坐标规律探求;先求得,然后解直角三角形分别求出,,,得到规律,再根据规律计算即可.
解:∵图案是用12个以点O为公共顶点的相似三角形组成形如海螺的图案,
∴,
∵,,
∴,
∵,
∴,
同理:,
依次类推:;
则点G的坐标为;
故答案为:.
20.
本题考查了一次函数和反比例函数规律探究;根据题意可以写出点、、、的坐标,从而可以发现各点的变化规律,从而可以写出点的坐标.
解:∵点的坐标为,
∴点的横坐标为1,
∴点的坐标为,
∴点的纵坐标为1,
∴点的坐标为,
同理点的横坐标为,
∴点的坐标为,
点的坐标为,
∴四个点一个循环,
∵余1,
∴点的坐标与点相同,是,
故答案为:.
本题考查一次函数图象上点的坐标特征、规律型,勾股定理,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
21.四
本题考查非负性,判断点所在的象限,根据非负性求出的值,根据的符号,判断出点A所在的象限即可.
解:∵,
∴,
∴,
∴点A的坐标为,在第四象限;
故答案为:四.
22.甲
本题考查函数图象的应用,解题的关键是明确题意,利用数形结合的思想解答问题.
从函数图象可知甲乙跑完全程的时间,即可确定答案.
解:根据图象可得甲到达终点用时秒,乙到达终点用时秒,
∴甲先到达终点,
故答案为:甲.
23. 8 12
本题考查动点的函数图象,相似三角形的判定和性质,从函数图象中有效的获取信息,是解题的关键:
(1)观察图象可知,当时,点与点重合,得到,利用直角三角形的面积公式进行计算,求出的值即可;
(2)根据图象当时,,此时,过点作,根据面积公式求出的长,证明,列出比例式求出的长,进而求出的长即可.
解:(1)观察图象可知,当时,点与点重合,
∵动点P,Q均以的速度从点同时出发,
∴,
∵,
∴;
故答案为:;
(2)由图象可知,当时,,此时,
过点作于点,如图:则:,
∵,
∴,
∵,
∴,
∴,
∴,
∴为的中点,
∴;
故答案为:12.
24.(1)
(2)
(3)叶瓣②还可以由叶瓣①逆时针旋转得到
本题考查了圆的性质、平面直角坐标系、旋转:
(1)先证明四边形是正方形即可得到坐标;
(2)根据,算出圆的周长即可得到叶瓣的周长;
(3)利用旋转即可.
(1)以原点,为圆心、以为半径作圆,两圆相交于两点
是正方形
(2)原点,为圆心、以为半径作圆
两个圆是等圆
叶瓣①的周长为:
(3)叶瓣②还可以由叶瓣①逆时针旋转得到.
25.(1)图见解析;
(2)图见解析
本题主要考查了中点坐标公式,坐标系中画位似图形,熟知中点坐标公式,位似图形的性质是解题的关键.
(1)根据两点中点坐标公式可确定点D的坐标,进而描出点D即可;
(2)根据点A和点的坐标可知,把B、C的横纵坐标都乘以即可得到的坐标,描出,并顺次连接即可.
(1)解:如图所示,点D即为边的中点,
∵,
∴点D的坐标为.
(2)解:如图所示,即为所求作的三角形.
26.(1),
(2)作图见解析,性质:当时,随的增大而减小,当时,随的增大而增大(不唯一);当时,随的增大而减小
(3)(或或或或)
本题考查函数解析式,一次函数的图象与性质,反比例函数的图象与性质,反比例函数与不等式,勾股定理,矩形的性质,熟练掌握相关性质,并能正确分段列出动点问题的相关线段是解题的关键.
(1)利用矩形性质和勾股定理得出,,分两部分:①当时;②当时,分别列出;过点作于点,利用等面积法求出,即可表示出的面积为,同理可得的面积为,再结合矩形的面积为与,即可列出;
(2)根据函数解析式画图即可,再根据函数图象写出性质;
(3)根据图象写出的图象在下方时对应的自变量的取值范围即可
(1)解:∵为矩形的对角线AC的中点,,,
∴,,
∴,
当时,,如图,
∴;
当时,,如图,
∴;
∴;
如图,过点作于点,
∵,
∴,
∴的面积为,
同理可得的面积为,
又∵矩形的面积为,
∴,
∴;
(2)解:作图如下:
性质:当时,随的增大而减小;当时,随的增大而增大(不唯一);当时,随的增大而减小;
(3)解:结合函数图象,可得时的取值范围为(或<或或或).
27.(1)
(2)
(3)7分或11分或13分
本题主要考查一次函数的应用和从函数图象获取信息,熟练掌握一次函数的应用是解题的关键.
(1)根据图象可直接进行求解A、C两区之间的距离,然后再结合甲的行进情况可求解a;
(2)求出,由图象可得,设直线的解析式为,进而问题可求解;
(3)由题意可分三种情况分别进行求解即可.
(1)解:由题意可得,A,C两区相距为(米),
由题意可知,表示甲到达B区的时间,则,
故答案为:
(2)由题意可知,点E表示机器人乙沿“勤学路”以10米/分的速度匀速到达了B区,
∴点E的横坐标为,
∴,
设直线的解析式为,把,代入得到,
,解得:,
∴线段所在直线的函数解析式为:;
(3)机器人乙行进的时间为x分时,甲和乙都未到达B区,相距30米,
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
机器人乙行进的时间为t分时,从B点返回,且甲仍在B区停留期间,相距30米,
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
机器人乙行进的时间为n分时,从B点返回途中,且甲离开B区向C区前进时,相距30米,
当时,甲机器人距B区的距离y(米)与机器人乙行进的时间x(分)之间的函数关系为,把,代入得到,
,解得:,
∴线段所在直线的函数解析式为:;
则,
解得,
即机器人乙行进的时间为分时,机器人甲、乙相距30米;
综上可知,机器人乙行进的时间7分或11分或13分时,机器人甲、乙相距30米.
同课章节目录
