专题24圆的有关计算与证明(16题)(含答案 解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用)
文档属性
| 名称 | 专题24圆的有关计算与证明(16题)(含答案 解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览



文档简介
专题24 圆的有关计算与证明(16题)
一、单选题
1.(2025·黑龙江绥化·中考真题)在中,如果的圆心角所对的弧长是,那么的半径是( )
A. B. C. D.
2.(2025·湖南·中考真题)如图,北京市某处位于北纬(即),东经,三沙市海域某处位于北纬(即),东经;设地球的半径约为千米,则在东经所在经线圈上的点和点之间的劣弧长约为( )
A.(千米) B.(千米)
C.(千米) D.(千米)
3.(2025·山东·中考真题)在中国古代文化中,玉璧寓意宇宙的广阔与秩序,也经常被视为君子修身齐家的象征.下图是某玉璧的平面示意图,由一个正方形的内切圆和外接圆组成.已知内切圆的半径是2,则图中阴影部分的面积是( )
A. B. C. D.
4.(2025·云南·中考真题)若一个圆锥的侧面展开图的圆心角度数为,母线长为,则该圆锥的底面圆的半径为( )
A. B. C. D.
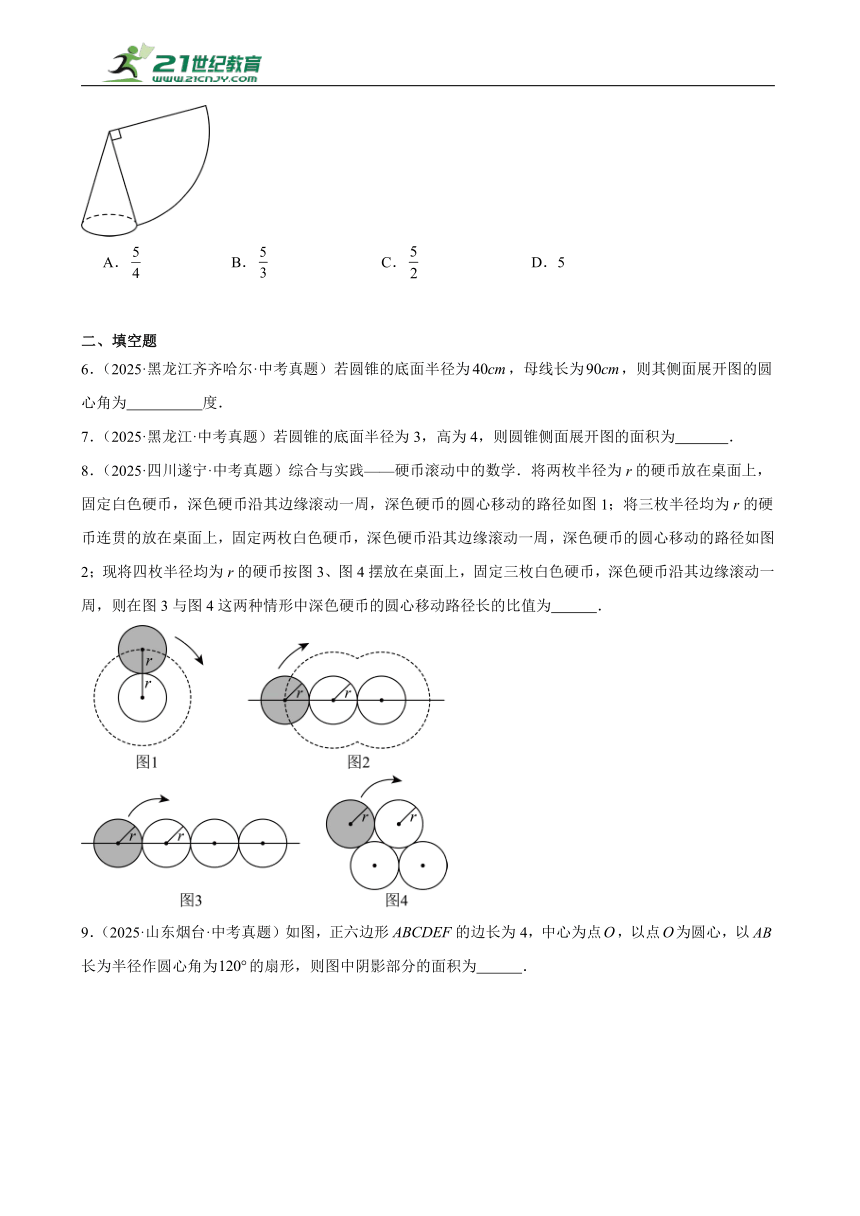
5.(2025·四川广安·中考真题)如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的母线长为5,则该圆锥的底面圆的半径为( )
A. B. C. D.5
二、填空题
6.(2025·黑龙江齐齐哈尔·中考真题)若圆锥的底面半径为,母线长为,则其侧面展开图的圆心角为 度.
7.(2025·黑龙江·中考真题)若圆锥的底面半径为3,高为4,则圆锥侧面展开图的面积为 .
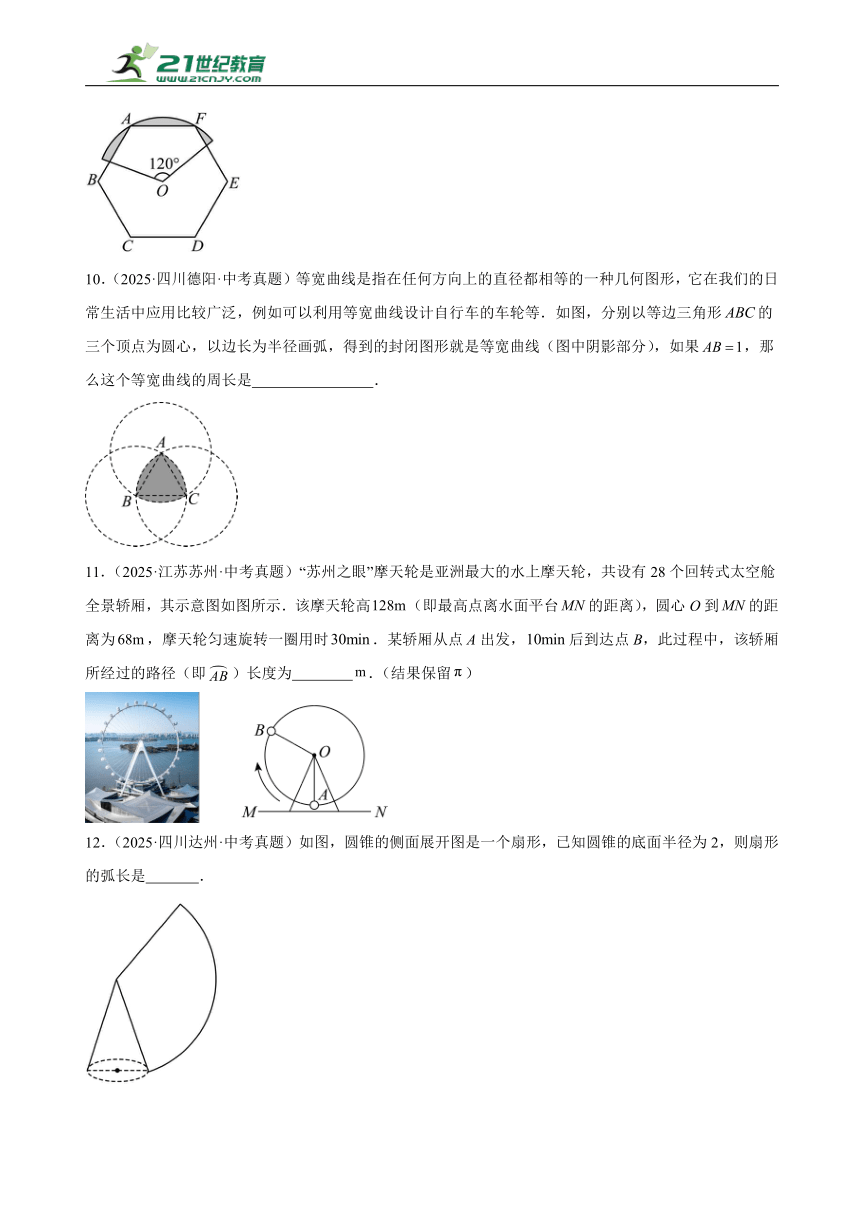
8.(2025·四川遂宁·中考真题)综合与实践——硬币滚动中的数学.将两枚半径为r的硬币放在桌面上,固定白色硬币,深色硬币沿其边缘滚动一周,深色硬币的圆心移动的路径如图1;将三枚半径均为r的硬币连贯的放在桌面上,固定两枚白色硬币,深色硬币沿其边缘滚动一周,深色硬币的圆心移动的路径如图2;现将四枚半径均为r的硬币按图3、图4摆放在桌面上,固定三枚白色硬币,深色硬币沿其边缘滚动一周,则在图3与图4这两种情形中深色硬币的圆心移动路径长的比值为 .
9.(2025·山东烟台·中考真题)如图,正六边形的边长为4,中心为点,以点为圆心,以长为半径作圆心角为的扇形,则图中阴影部分的面积为 .
10.(2025·四川德阳·中考真题)等宽曲线是指在任何方向上的直径都相等的一种几何图形,它在我们的日常生活中应用比较广泛,例如可以利用等宽曲线设计自行车的车轮等.如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形就是等宽曲线(图中阴影部分),如果,那么这个等宽曲线的周长是 .
11.(2025·江苏苏州·中考真题)“苏州之眼”摩天轮是亚洲最大的水上摩天轮,共设有28个回转式太空舱全景轿厢,其示意图如图所示.该摩天轮高(即最高点离水面平台的距离),圆心O到的距离为,摩天轮匀速旋转一圈用时.某轿厢从点A出发,后到达点B,此过程中,该轿厢所经过的路径(即)长度为 .(结果保留)
12.(2025·四川达州·中考真题)如图,圆锥的侧面展开图是一个扇形,已知圆锥的底面半径为2,则扇形的弧长是 .
三、解答题
13.(2025·黑龙江·中考真题)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,的三个顶点坐标分别为.
(1)将向上平移5个单位长度,再向右平移1个单位长度,得到,画出两次平移后的,并写出点的坐标;
(2)画出绕原点O逆时针旋转后得到的,并写出点的坐标;
(3)在(2)的条件下,求点旋转到点的过程中,所经过的路径长(结果保留π).
14.(2025·黑龙江绥化·中考真题)尺规作图(温馨提示:以下作图均不写作法,但需保留作图痕迹)
[初步尝试]
如图(1)用无刻度的直尺和圆规作一条经过圆心的直线,使扇形的面积被直线平分.
[拓展探究]
如图(2),若扇形的圆心角为,请你用无刻度的直尺和圆规作一条以点为圆心的弧,交于点,交于点,使扇形的面积与扇形的面积比为.
15.(2025·江苏扬州·中考真题)材料的疏水性
扬州宝应是荷藕之乡.“微风忽起吹莲叶,青玉盘中泻水银”,莲叶上的水滴来回滚动,不易渗入莲叶内部,这说明莲叶具有较强的疏水性.疏水性是指材料与水相互排斥的一种性质.
【概念理解】
材料疏水性的强弱通常用接触角的大小来描述.材料上的水滴可以近似的看成球或球的一部分,经过球心的纵截面如图1所示,接触角是过固、液、气三相接触点(点或点)所作的气 液界线的切线与固 液界线的夹角,图1中的就是水滴的一个接触角.
(1)请用无刻度的直尺和圆规作出图2中水滴的一个接触角,并用三个大写字母表示接触角;(保留作图痕迹,写出必要的文字说明)
(2)材料的疏水性随着接触角的变大而______(选填“变强”“不变”“变弱”).
【实践探索】
实践中,可以通过测量水滴经过球心的高度和底面圆的半径,求出的度数,进而求出接触角的度数(如图3).
(3)请探索图3中接触角与之间的数量关系(用等式表示),并说明理由.
【创新思考】
(4)材料的疏水性除了用接触角以及图3中与相关的量描述外,还可以用什么量来描述,请你提出一个合理的设想,并说明疏水性随着此量的变化而如何变化.
16.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
《专题24 圆的有关计算与证明(16题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5
答案 A C D B A
1.A
本题考查弧长公式,根据圆心角对应的弧长公式,代入已知条件求解半径即可.
解:根据弧长公式:,其中,
代入得:
解得:
故选:A.
2.C
本题主要考查了求弧长,根据题意求出的度数,再根据弧长公式求解即可.
解;由题意得,,
∴劣弧的长为千米,
故选:C.
3.D
本题主要考查了正方形的内切圆、外切圆、勾股定理等知识点,掌握数形结合思想成为解题的关键.
如图:连接相交于O,由正方形的内切圆的半径是2,,,再运用勾股定理可得,则,最后根据圆的面积公式求解即可.
解:如图:连接相交于O,
∵正方形的内切圆的半径是2,
∴,,
∴,,
∴图中阴影部分的面积是.
故选D.
4.B
本题考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开图扇形的弧长.
设圆锥底面圆半径为,根据圆锥侧面展开图的扇形弧长等于底面圆的周长得到,即可求解半径.
解:设圆锥底面圆半径为,
由题意得:,
解得,
因此,该圆锥的底面圆半径为,
故选:B.
5.A
本题考查了与圆锥相关的计算,熟知圆锥侧面展开后是扇形及与圆锥的底面半径的关系是解题的关键;
先计算圆锥展开图的扇形的弧长,再进一步计算即可
解:圆锥侧面展开图的扇形的弧长,
∴该圆锥的底面圆的半径为;
故选:A
6.160
本题综合考查有关扇形和圆锥的相关计算.圆锥的底面半径为,则底面圆的周长是,圆锥的底面周长等于侧面展开图的扇形弧长,即侧面展开图的扇形弧长是,母线长为即侧面展开图的扇形的半径长是.根据弧长公式即可计算.
解:根据弧长的公式得到:
,
解得.
即侧面展开图的圆心角为160度.
故答案为:160.
7.
本题考查求圆锥的侧面积,根据勾股定理求出母线长,再根据侧面积公式进行计算即可.
解:∵圆锥的底面半径为3,高为4,
∴圆锥的母线长为,
∴圆锥侧面展开图的面积为;
故答案为:.
8.
本题考查了弧长公式,等边三角形的判定与性质,正确掌握相关性质内容是解题的关键.先理解题意,把深色硬币的圆心移动路径都画出来,根据三边都等于,证明是等边三角形,同理得出其他三角形都是等边三角形,再求出每条弧长,再加起来得出图3与图4这两种情形中深色硬币的圆心移动路径长,再进行求解,即可作答.
解:依题意,,
则是等边三角形;
则,
同理得、、是等边三角形,
则
∴
∴,
∴,
∴;
依题意,,
∴是等边三角形;
则,
同理得、、是等边三角形,
则
则,
则
故答案为:.
9.
连接、、,过点O作于点M,根据正六边形的性质得出,,,证明和为等边三角形,求出,证明,得出,得出,根据求出结果即可.
解:连接、、,过点O作于点M,如图所示:
∵六边形为正六边形,
∴,,,
∴和为等边三角形,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴
.
故答案为:.
本题主要考查了正六边形的性质,勾股定理,等边三角形的判定和性质,扇形面积计算,三角形全等的判定和性质,解题的关键是熟练掌握正六边形的性质.
10.
本题考查了弧长的计算,等边三角形的性质,利用弧长计算公式计算即可.
解:∵是等边三角形,
∴,
∴,
∴这个等宽曲线的周长为.
故答案为:
11.
本题主要考查了弧长计算,熟练掌握弧长公式是解题的关键.先求出摩天轮半径,再求出,最后根据弧长公式求出结果即可.
解:∵最高点离水面平台的距离为,圆心O到的距离为,
∴摩天轮的半径为,
∵摩天轮匀速旋转一圈用时,轿厢从点A出发,后到达点B,
∴,
∴该轿厢所经过的路径长度为:
.
故答案为:.
12.
本题考查了圆锥的相关计算,明确扇形的弧长=圆锥底面圆的周长是解题的关键;
根据扇形的弧长=圆锥底面圆的周长计算求解即可.
解:扇形的弧长=圆锥底面圆的周长;
故答案为:.
13.(1)作图见解析,
(2)作图见解析,
(3)
本题考查了平移作图,旋转作图,弧长公式,勾股定理等知识点,熟练掌握各知识点并灵活运用是解题的关键.
(1)分别描出平移后的点,再顺次连接即可得到,根据点的平移方式即可求解;
(2)将点分别绕原点O逆时针旋转得到点,再顺次连接即可,即可写出点的坐标;
(3)先由勾股定理求出,再由弧长公式求解即可.
(1)解:如图,即为所求:
∵,
∴向上平移5个单位长度,再向右平移1个单位长度得到,即;
(2)解:如图,即为所求,;
(3)解:,
∴点旋转到点的过程中,所经过的路径长为
14.[初步尝试]见解析;[拓展探究]见解析
本题主要考查了扇形的面积,基本作图,熟练掌握扇形的面积公式和尺规作图是解题的关键.
[初步尝试] 经过圆心的直线平分扇形的面积,作圆心角的角平分线或作扇形弧对应弦的垂直平分线;
[拓展探究]根据扇形面积公式,扇形面积之比等于扇形半径的平方之比,从而得到 扇形的面积与扇形半径之比为,只要画出或的中点即可.方法一:作扇形半径的垂直平分线找到中点,然后以为半径作弧交半径于点.方法二:扇形的圆心角为,根据含的直角三角形是斜边的一半,过点作出的垂线,构造直角三角形,取垂线段的长度为半径,以为圆心画弧即可.
解:[初步尝试]
作法一:如图所示
①连接,分别以点和点为圆心,大于的长为半径作弧,
两弧交于点,标注出点
②画直线
③直线即为所求
作法二:如图所示
①以为圆心,适当长为半径画弧,交于点,交于点,
②分别以、为圆心,大于的长为半径作弧,两弧交于点,标注出点.
③画直线,直线即为所求
[拓展探究]
扇形的面积与扇形的面积比为,设扇形的半径为,扇形的半径为
扇形的面积∶扇形的面积
只要画出或的中点即可
作法一:
①作的垂直平分线交于点,标注出点
②以为圆心长为半径画弧,交于点,标注出点
③弧即为所求.(同理作的垂直平分线也可得分)
作法二:
过点作出的垂线或者过点作的垂线,取垂线段的长度为半径,以为圆心画弧即可.(依据:含的直角三角形是斜边的一半)
15.(1)图见解析(2)变强(3),理由见解析(4)见解析(答案不唯一)
本题考查尺规作图—复杂作图,切线的判定和性质,熟练掌握新定义,切线的判定和性质,是解题的关键.
(1)圆弧上取一点,交界面与圆弧的交点为,连接,分别作的中垂线,交于点,则点为圆弧的圆心,连接,过点作,则为圆的切线,即为所求;
(2)根据题意,可知,接触角越大,水滴越趋近于球形,疏水性越强,进行作答即可;
(3)连接,等边对等角,得到,切线的性质,结合等角的余角相等,得到,进而得到即可;
(4)可以根据,进行判断,根据越大,水滴越趋近于球形,疏水性越强进行作答即可.
解:(1)①圆弧上取一点,交界面与圆弧的交点为,连接;
②分别作的中垂线,交于点,则点为圆弧的圆心;
③连接,过点作,则为圆的切线,故即为所求;
(2)由题意和图,可知,接触角越大,水滴越趋近于球形,疏水性越强,
故材料的疏水性随着接触角的变大而变强;
故答案为:变强;
(3),理由如下:
连接,则:,
∴,
∵为切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(4)∵水滴弧的长度为:,
∴,
∴可以根据的大小,进行判断,越大,水滴越趋近于球形,疏水性越强(答案不唯一).
16.(1)
(2)
本题考查了解直角三角形的应用,圆的切线的性质,弧长公式,熟练掌握各知识点并灵活运用是解题的关键.
(1)由圆的切线的性质得到,再由直角三角形锐角互余即可求解;
(2)先解,设,,再解得到,求出,求出半径,再由弧长公式即可求解.
(1)解:∵直线与所在相切于点,
∴,
∵,
∴;
(2)解:∵直线与所在相切于点,
∴,
∵,
∴,
设,
∴,
∵,
∴,
∵在中,,
∴,
∴,
解得:,
∴,
∴的弧长为:,
答:的弧长为.
一、单选题
1.(2025·黑龙江绥化·中考真题)在中,如果的圆心角所对的弧长是,那么的半径是( )
A. B. C. D.
2.(2025·湖南·中考真题)如图,北京市某处位于北纬(即),东经,三沙市海域某处位于北纬(即),东经;设地球的半径约为千米,则在东经所在经线圈上的点和点之间的劣弧长约为( )
A.(千米) B.(千米)
C.(千米) D.(千米)
3.(2025·山东·中考真题)在中国古代文化中,玉璧寓意宇宙的广阔与秩序,也经常被视为君子修身齐家的象征.下图是某玉璧的平面示意图,由一个正方形的内切圆和外接圆组成.已知内切圆的半径是2,则图中阴影部分的面积是( )
A. B. C. D.
4.(2025·云南·中考真题)若一个圆锥的侧面展开图的圆心角度数为,母线长为,则该圆锥的底面圆的半径为( )
A. B. C. D.
5.(2025·四川广安·中考真题)如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的母线长为5,则该圆锥的底面圆的半径为( )
A. B. C. D.5
二、填空题
6.(2025·黑龙江齐齐哈尔·中考真题)若圆锥的底面半径为,母线长为,则其侧面展开图的圆心角为 度.
7.(2025·黑龙江·中考真题)若圆锥的底面半径为3,高为4,则圆锥侧面展开图的面积为 .
8.(2025·四川遂宁·中考真题)综合与实践——硬币滚动中的数学.将两枚半径为r的硬币放在桌面上,固定白色硬币,深色硬币沿其边缘滚动一周,深色硬币的圆心移动的路径如图1;将三枚半径均为r的硬币连贯的放在桌面上,固定两枚白色硬币,深色硬币沿其边缘滚动一周,深色硬币的圆心移动的路径如图2;现将四枚半径均为r的硬币按图3、图4摆放在桌面上,固定三枚白色硬币,深色硬币沿其边缘滚动一周,则在图3与图4这两种情形中深色硬币的圆心移动路径长的比值为 .
9.(2025·山东烟台·中考真题)如图,正六边形的边长为4,中心为点,以点为圆心,以长为半径作圆心角为的扇形,则图中阴影部分的面积为 .
10.(2025·四川德阳·中考真题)等宽曲线是指在任何方向上的直径都相等的一种几何图形,它在我们的日常生活中应用比较广泛,例如可以利用等宽曲线设计自行车的车轮等.如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形就是等宽曲线(图中阴影部分),如果,那么这个等宽曲线的周长是 .
11.(2025·江苏苏州·中考真题)“苏州之眼”摩天轮是亚洲最大的水上摩天轮,共设有28个回转式太空舱全景轿厢,其示意图如图所示.该摩天轮高(即最高点离水面平台的距离),圆心O到的距离为,摩天轮匀速旋转一圈用时.某轿厢从点A出发,后到达点B,此过程中,该轿厢所经过的路径(即)长度为 .(结果保留)
12.(2025·四川达州·中考真题)如图,圆锥的侧面展开图是一个扇形,已知圆锥的底面半径为2,则扇形的弧长是 .
三、解答题
13.(2025·黑龙江·中考真题)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,的三个顶点坐标分别为.
(1)将向上平移5个单位长度,再向右平移1个单位长度,得到,画出两次平移后的,并写出点的坐标;
(2)画出绕原点O逆时针旋转后得到的,并写出点的坐标;
(3)在(2)的条件下,求点旋转到点的过程中,所经过的路径长(结果保留π).
14.(2025·黑龙江绥化·中考真题)尺规作图(温馨提示:以下作图均不写作法,但需保留作图痕迹)
[初步尝试]
如图(1)用无刻度的直尺和圆规作一条经过圆心的直线,使扇形的面积被直线平分.
[拓展探究]
如图(2),若扇形的圆心角为,请你用无刻度的直尺和圆规作一条以点为圆心的弧,交于点,交于点,使扇形的面积与扇形的面积比为.
15.(2025·江苏扬州·中考真题)材料的疏水性
扬州宝应是荷藕之乡.“微风忽起吹莲叶,青玉盘中泻水银”,莲叶上的水滴来回滚动,不易渗入莲叶内部,这说明莲叶具有较强的疏水性.疏水性是指材料与水相互排斥的一种性质.
【概念理解】
材料疏水性的强弱通常用接触角的大小来描述.材料上的水滴可以近似的看成球或球的一部分,经过球心的纵截面如图1所示,接触角是过固、液、气三相接触点(点或点)所作的气 液界线的切线与固 液界线的夹角,图1中的就是水滴的一个接触角.
(1)请用无刻度的直尺和圆规作出图2中水滴的一个接触角,并用三个大写字母表示接触角;(保留作图痕迹,写出必要的文字说明)
(2)材料的疏水性随着接触角的变大而______(选填“变强”“不变”“变弱”).
【实践探索】
实践中,可以通过测量水滴经过球心的高度和底面圆的半径,求出的度数,进而求出接触角的度数(如图3).
(3)请探索图3中接触角与之间的数量关系(用等式表示),并说明理由.
【创新思考】
(4)材料的疏水性除了用接触角以及图3中与相关的量描述外,还可以用什么量来描述,请你提出一个合理的设想,并说明疏水性随着此量的变化而如何变化.
16.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
《专题24 圆的有关计算与证明(16题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5
答案 A C D B A
1.A
本题考查弧长公式,根据圆心角对应的弧长公式,代入已知条件求解半径即可.
解:根据弧长公式:,其中,
代入得:
解得:
故选:A.
2.C
本题主要考查了求弧长,根据题意求出的度数,再根据弧长公式求解即可.
解;由题意得,,
∴劣弧的长为千米,
故选:C.
3.D
本题主要考查了正方形的内切圆、外切圆、勾股定理等知识点,掌握数形结合思想成为解题的关键.
如图:连接相交于O,由正方形的内切圆的半径是2,,,再运用勾股定理可得,则,最后根据圆的面积公式求解即可.
解:如图:连接相交于O,
∵正方形的内切圆的半径是2,
∴,,
∴,,
∴图中阴影部分的面积是.
故选D.
4.B
本题考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开图扇形的弧长.
设圆锥底面圆半径为,根据圆锥侧面展开图的扇形弧长等于底面圆的周长得到,即可求解半径.
解:设圆锥底面圆半径为,
由题意得:,
解得,
因此,该圆锥的底面圆半径为,
故选:B.
5.A
本题考查了与圆锥相关的计算,熟知圆锥侧面展开后是扇形及与圆锥的底面半径的关系是解题的关键;
先计算圆锥展开图的扇形的弧长,再进一步计算即可
解:圆锥侧面展开图的扇形的弧长,
∴该圆锥的底面圆的半径为;
故选:A
6.160
本题综合考查有关扇形和圆锥的相关计算.圆锥的底面半径为,则底面圆的周长是,圆锥的底面周长等于侧面展开图的扇形弧长,即侧面展开图的扇形弧长是,母线长为即侧面展开图的扇形的半径长是.根据弧长公式即可计算.
解:根据弧长的公式得到:
,
解得.
即侧面展开图的圆心角为160度.
故答案为:160.
7.
本题考查求圆锥的侧面积,根据勾股定理求出母线长,再根据侧面积公式进行计算即可.
解:∵圆锥的底面半径为3,高为4,
∴圆锥的母线长为,
∴圆锥侧面展开图的面积为;
故答案为:.
8.
本题考查了弧长公式,等边三角形的判定与性质,正确掌握相关性质内容是解题的关键.先理解题意,把深色硬币的圆心移动路径都画出来,根据三边都等于,证明是等边三角形,同理得出其他三角形都是等边三角形,再求出每条弧长,再加起来得出图3与图4这两种情形中深色硬币的圆心移动路径长,再进行求解,即可作答.
解:依题意,,
则是等边三角形;
则,
同理得、、是等边三角形,
则
∴
∴,
∴,
∴;
依题意,,
∴是等边三角形;
则,
同理得、、是等边三角形,
则
则,
则
故答案为:.
9.
连接、、,过点O作于点M,根据正六边形的性质得出,,,证明和为等边三角形,求出,证明,得出,得出,根据求出结果即可.
解:连接、、,过点O作于点M,如图所示:
∵六边形为正六边形,
∴,,,
∴和为等边三角形,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴
.
故答案为:.
本题主要考查了正六边形的性质,勾股定理,等边三角形的判定和性质,扇形面积计算,三角形全等的判定和性质,解题的关键是熟练掌握正六边形的性质.
10.
本题考查了弧长的计算,等边三角形的性质,利用弧长计算公式计算即可.
解:∵是等边三角形,
∴,
∴,
∴这个等宽曲线的周长为.
故答案为:
11.
本题主要考查了弧长计算,熟练掌握弧长公式是解题的关键.先求出摩天轮半径,再求出,最后根据弧长公式求出结果即可.
解:∵最高点离水面平台的距离为,圆心O到的距离为,
∴摩天轮的半径为,
∵摩天轮匀速旋转一圈用时,轿厢从点A出发,后到达点B,
∴,
∴该轿厢所经过的路径长度为:
.
故答案为:.
12.
本题考查了圆锥的相关计算,明确扇形的弧长=圆锥底面圆的周长是解题的关键;
根据扇形的弧长=圆锥底面圆的周长计算求解即可.
解:扇形的弧长=圆锥底面圆的周长;
故答案为:.
13.(1)作图见解析,
(2)作图见解析,
(3)
本题考查了平移作图,旋转作图,弧长公式,勾股定理等知识点,熟练掌握各知识点并灵活运用是解题的关键.
(1)分别描出平移后的点,再顺次连接即可得到,根据点的平移方式即可求解;
(2)将点分别绕原点O逆时针旋转得到点,再顺次连接即可,即可写出点的坐标;
(3)先由勾股定理求出,再由弧长公式求解即可.
(1)解:如图,即为所求:
∵,
∴向上平移5个单位长度,再向右平移1个单位长度得到,即;
(2)解:如图,即为所求,;
(3)解:,
∴点旋转到点的过程中,所经过的路径长为
14.[初步尝试]见解析;[拓展探究]见解析
本题主要考查了扇形的面积,基本作图,熟练掌握扇形的面积公式和尺规作图是解题的关键.
[初步尝试] 经过圆心的直线平分扇形的面积,作圆心角的角平分线或作扇形弧对应弦的垂直平分线;
[拓展探究]根据扇形面积公式,扇形面积之比等于扇形半径的平方之比,从而得到 扇形的面积与扇形半径之比为,只要画出或的中点即可.方法一:作扇形半径的垂直平分线找到中点,然后以为半径作弧交半径于点.方法二:扇形的圆心角为,根据含的直角三角形是斜边的一半,过点作出的垂线,构造直角三角形,取垂线段的长度为半径,以为圆心画弧即可.
解:[初步尝试]
作法一:如图所示
①连接,分别以点和点为圆心,大于的长为半径作弧,
两弧交于点,标注出点
②画直线
③直线即为所求
作法二:如图所示
①以为圆心,适当长为半径画弧,交于点,交于点,
②分别以、为圆心,大于的长为半径作弧,两弧交于点,标注出点.
③画直线,直线即为所求
[拓展探究]
扇形的面积与扇形的面积比为,设扇形的半径为,扇形的半径为
扇形的面积∶扇形的面积
只要画出或的中点即可
作法一:
①作的垂直平分线交于点,标注出点
②以为圆心长为半径画弧,交于点,标注出点
③弧即为所求.(同理作的垂直平分线也可得分)
作法二:
过点作出的垂线或者过点作的垂线,取垂线段的长度为半径,以为圆心画弧即可.(依据:含的直角三角形是斜边的一半)
15.(1)图见解析(2)变强(3),理由见解析(4)见解析(答案不唯一)
本题考查尺规作图—复杂作图,切线的判定和性质,熟练掌握新定义,切线的判定和性质,是解题的关键.
(1)圆弧上取一点,交界面与圆弧的交点为,连接,分别作的中垂线,交于点,则点为圆弧的圆心,连接,过点作,则为圆的切线,即为所求;
(2)根据题意,可知,接触角越大,水滴越趋近于球形,疏水性越强,进行作答即可;
(3)连接,等边对等角,得到,切线的性质,结合等角的余角相等,得到,进而得到即可;
(4)可以根据,进行判断,根据越大,水滴越趋近于球形,疏水性越强进行作答即可.
解:(1)①圆弧上取一点,交界面与圆弧的交点为,连接;
②分别作的中垂线,交于点,则点为圆弧的圆心;
③连接,过点作,则为圆的切线,故即为所求;
(2)由题意和图,可知,接触角越大,水滴越趋近于球形,疏水性越强,
故材料的疏水性随着接触角的变大而变强;
故答案为:变强;
(3),理由如下:
连接,则:,
∴,
∵为切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(4)∵水滴弧的长度为:,
∴,
∴可以根据的大小,进行判断,越大,水滴越趋近于球形,疏水性越强(答案不唯一).
16.(1)
(2)
本题考查了解直角三角形的应用,圆的切线的性质,弧长公式,熟练掌握各知识点并灵活运用是解题的关键.
(1)由圆的切线的性质得到,再由直角三角形锐角互余即可求解;
(2)先解,设,,再解得到,求出,求出半径,再由弧长公式即可求解.
(1)解:∵直线与所在相切于点,
∴,
∵,
∴;
(2)解:∵直线与所在相切于点,
∴,
∵,
∴,
设,
∴,
∵,
∴,
∵在中,,
∴,
∴,
解得:,
∴,
∴的弧长为:,
答:的弧长为.
同课章节目录
