专题25图形的平移翻折对称旋转(33题)(含答案 解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用)
文档属性
| 名称 | 专题25图形的平移翻折对称旋转(33题)(含答案 解析)-【真题汇编】2025年中考数学真题分类汇编(全国通用) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览



文档简介
专题25 图形的平移翻折对称(33题)
一、单选题
1.(2025·湖南·中考真题)在平面直角坐标系中,将点向右平移个单位长度到处,则点的坐标为( )
A. B. C. D.
2.(2025·四川自贡·中考真题)如图,在平面直角坐标系中,将平移,得到,点在坐标轴上.若,则点坐标为( )
A. B. C. D.
3.(2025·四川眉山·中考真题)在平面直角坐标系中,将点向右平移2个单位到点B,则点B的坐标为( )
A. B. C. D.
4.(2025·黑龙江绥化·中考真题)下列数学符号是轴对称图形的是( )
A. B. C. D.
5.(2025·黑龙江·中考真题)我国古代有很多关于数学的伟大发现,其中包括很多美丽的图案,下列图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.(2025·天津·中考真题)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
7.(2025·江苏扬州·中考真题)窗棂是中国传统木构建筑的重要元素,既散发着古典之韵,又展现了几何之美.下列窗棂图案中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
8.(2025·湖南·中考真题)武术是我国传统的体育项目.下列武术动作图形中,是轴对称图形的是( )
A. B. C. D.
9.(2025·湖北·中考真题)在下列事件中,不可能事件是( )
A.投掷一枚硬币,正面向上 B.从只有红球的袋子中摸出黄球
C.任意画一个圆,它是轴对称图形 D.射击运动员射击一次,命中靶心
10.(2025·新疆·中考真题)下列四种化学仪器的示意图中,是轴对称图形的是( )
A. B. C. D.
11.(2025·四川泸州·中考真题)下列人工智能助手图标中,是轴对称图形的是( )
A. B. C. D.
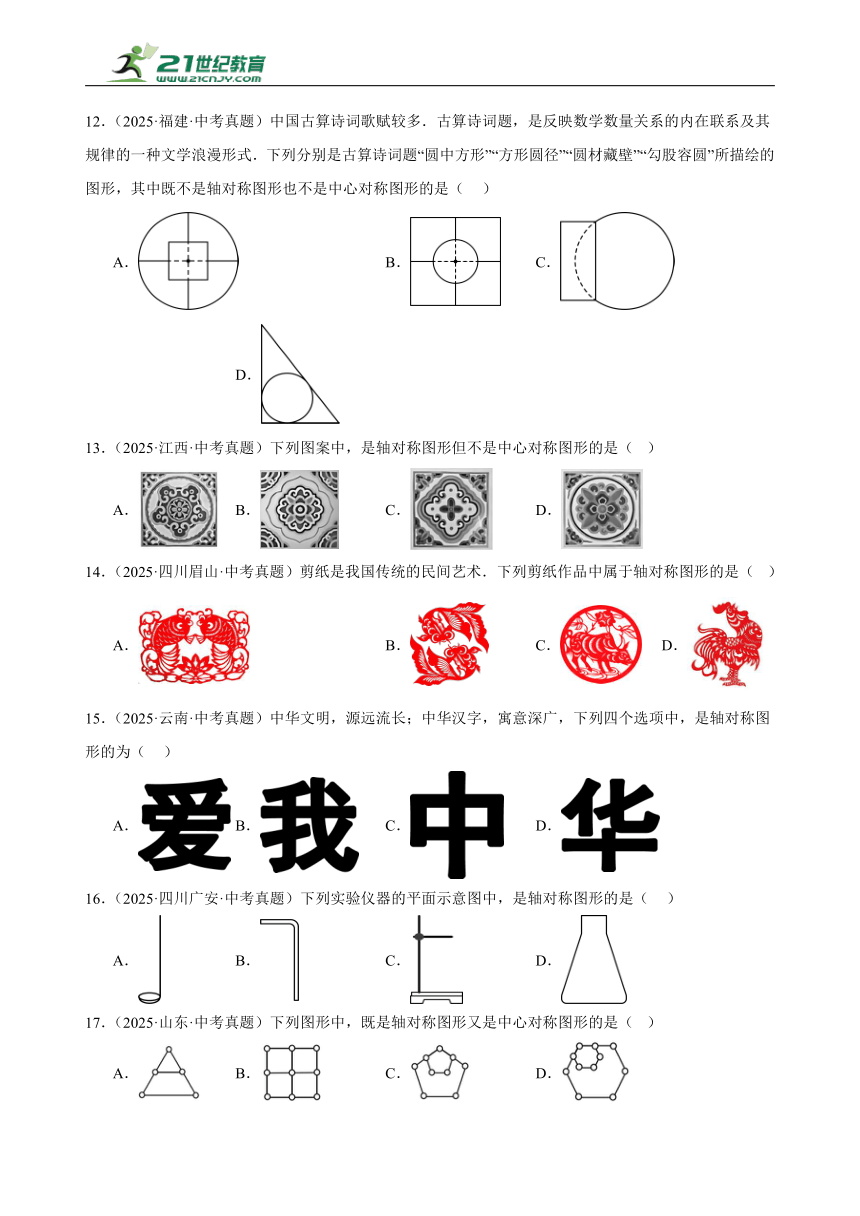
12.(2025·福建·中考真题)中国古算诗词歌赋较多.古算诗词题,是反映数学数量关系的内在联系及其规律的一种文学浪漫形式.下列分别是古算诗词题“圆中方形”“方形圆径”“圆材藏壁”“勾股容圆”所描绘的图形,其中既不是轴对称图形也不是中心对称图形的是( )
A. B. C. D.
13.(2025·江西·中考真题)下列图案中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
14.(2025·四川眉山·中考真题)剪纸是我国传统的民间艺术.下列剪纸作品中属于轴对称图形的是( )
A. B. C. D.
15.(2025·云南·中考真题)中华文明,源远流长;中华汉字,寓意深广,下列四个选项中,是轴对称图形的为( )
A. B. C. D.
16.(2025·四川广安·中考真题)下列实验仪器的平面示意图中,是轴对称图形的是( )
A. B. C. D.
17.(2025·山东·中考真题)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
18.(2025·四川遂宁·中考真题)汉字作为中华优秀传统文化的根脉和重要载体,在发展过程中演变出多种字体,给人以美的享受.下面是“遂宁之美”四个字的篆书,能看作是轴对称图形的是( )
A. B. C. D.
19.(2025·四川内江·中考真题)古钱币是我国珍贵的历史文化遗产.下列选项是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
20.(2025·四川凉山·中考真题)以下字母是轴对称图形的是( )
A. B. C. D.
21.(2025·重庆·中考真题)下列图案中,是轴对称图形的是( )
A. B. C. D.
二、填空题
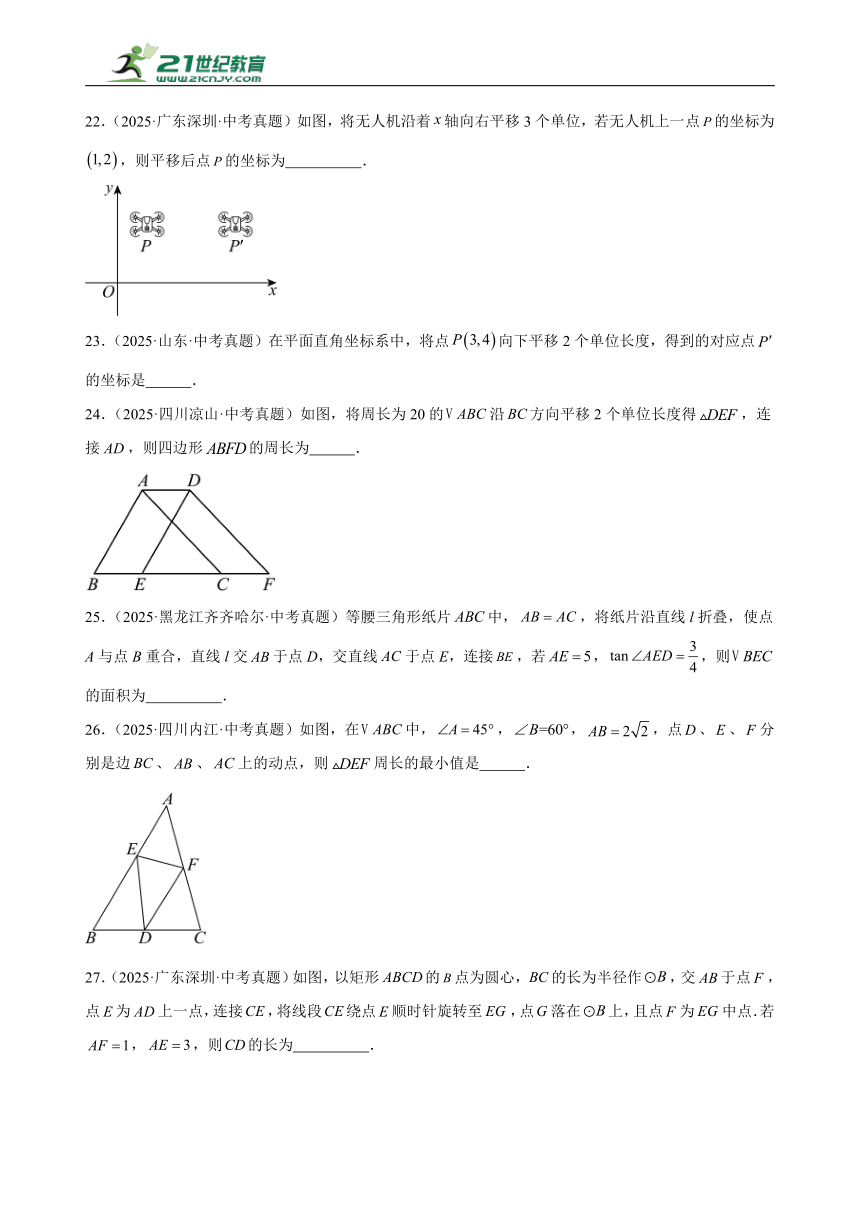
22.(2025·广东深圳·中考真题)如图,将无人机沿着轴向右平移3个单位,若无人机上一点的坐标为,则平移后点的坐标为 .
23.(2025·山东·中考真题)在平面直角坐标系中,将点向下平移2个单位长度,得到的对应点的坐标是 .
24.(2025·四川凉山·中考真题)如图,将周长为20的沿方向平移2个单位长度得,连接,则四边形的周长为 .
25.(2025·黑龙江齐齐哈尔·中考真题)等腰三角形纸片中,,将纸片沿直线l折叠,使点A与点B重合,直线l交于点D,交直线于点E,连接,若,,则的面积为 .
26.(2025·四川内江·中考真题)如图,在中,,,,点、、分别是边、、上的动点,则周长的最小值是 .
27.(2025·广东深圳·中考真题)如图,以矩形的点为圆心,的长为半径作,交于点,点为上一点,连接,将线段绕点顺时针旋转至,点落在上,且点为中点.若,,则的长为 .
28.(2025·山西·中考真题)如图,在平面直角坐标系中,点的坐标为,将线段绕点逆时针旋转,则点对应点的坐标为 .
三、解答题
29.(2025·四川遂宁·中考真题)如图,在平面直角坐标系中,二次函数(为常数)的图像与轴交于、两点,交轴于点,对称轴为直线.
(1)求二次函数关系式.
(2)连接,抛物线上是否存在点,使,若存在,求出点的坐标,若不存在,说明理由.
(3)在轴上方的抛物线上找一点,作射线,使,点是线段上的一动点,过点作轴,垂足为点,连结,求的最小值.
30.(2025·山东烟台·中考真题)如图,是矩形的对角线,请按以下要求解决问题:
(1)利用尺规作,使与关于直线成轴对称(不写作法,保留作图痕迹);
(2)在(1)的条件下,若交于点,,,求的长.
31.(2025·四川成都·中考真题)如图,在中,点在边上,点关于直线的对称点落在内,射线交射线于点,交射线于点,射线交边于点.
【特例感知】
(1)如图1,当时,点在延长线上,求证:;
【问题探究】
(2)在(1)的条件下,若,,求的长;
【拓展延伸】
(3)如图2,当时,点在边上,若,求的值.(用含的代数式表示)
32.(2025·四川凉山·中考真题)某型号起重机吊起一货物M在空中保持静止状态时,如图1,货物M与点O的连线恰好平行于地面,米,.(参考数据:,结果精确到1米)
(1)求直吊臂的长;
(2)如图2,直吊臂与的长度保持不变,绕点O逆时针旋转,当时,货物M上升了多少米?
33.(2025·四川达州·中考真题)综合与实践
问题提出:探究图形中线段之间的数量关系,通常将一个图形分割成几个图形,根据面积不变,获得线段之间的数量关系.
探究发现:如图1,在中,,是边上一点,过点作于,于,过点作于.连结,由图形面积分割法得:______;则____________.
实践应用:如图2,是等边三角形,,点是边上一点,连结.将线段绕点逆时针旋转得,连结交于,过点作于,于,当时,求的值.
拓展延伸:如图3,已知是半圆的直径,,是弦,,是上一点,,垂足为,,求的值.
《专题25 图形的平移翻折对称(33题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D B B C C B C
题号 11 12 13 14 15 16 17 18 19 20
答案 C D A A C D B D D B
题号 21
答案 B
1.B
本题主要考查点的平移,掌握平移规律是关键.
根据平面直角坐标系中点的平移规律,向右平移时横坐标增加,纵坐标不变,即可解题.
解:点向右平移3个单位长度,横坐标需加3,即,纵坐标2保持不变,
∴平移后的点坐标为,
故选:B.
2.B
本题考查解直角三角形,相似三角形的判定和性质,坐标与图形变换—平移,熟练掌握相关知识点,添加辅助线构造相似三角形,是解题的关键.过点作轴,作交的延长线于点,证明,得到,根据点的坐标,结合的值,求出,平移求出点坐标,进而得到平移规则,再求出点坐标即可.
解:过点作轴,作交的延长线于点,则:
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵平移,
∴,
∴,
∴将点先向右平移10个单位,再向下平移3个单位得到点,
∴将点先向右平移10个单位,再向下平移3个单位得到点,
∴;
故选B.
3.C
本题主要考查了坐标与图形变化﹣平移.掌握平移的规律“左右横,上下纵,正加负减”是解答本题的关键.
根据平移规律,向右平移2个单位时,点的横坐标增加2,纵坐标不变,即可解答.
解:点向右平移2个单位,横坐标变为,纵坐标保持3不变.
所以,点的坐标为,、
故选:C.
4.D
本题考查了轴对称图形的定义,熟知轴对称图形的概念是解题的关键;
根据轴对称图形的定义:如果将一个图形沿着某条直线折叠,直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,即可解答.
解: 选项中的数学符号是轴对称图形的是,其它的都不是;
故选:D.
5.B
本题考查了中心对称图形和轴对称图形的定义,能熟记中心对称图形和轴对称图形的定义是解此题的关键.中心对称图形是在平面内,把一个图形绕某一定点旋转,能够与自身重合的图形;轴对称图形是在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.依据定义判断即可.
解:A中、是轴对称图形,不是中心对称图形,不符合题意;
B中、既是轴对称图形,又是中心对称图形,符合题意;
C中、是中心对称图形,不是轴对称图形,不符合题意;
D中、既不是轴对称图形,也不是中心对称图形,不符合题意;
故选:B.
6.B
本题主要查了轴对称图形.根据轴对称图形得定义,逐项判断,即可求解.
解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:B
7.C
本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、既是轴对称图形,又是中心对称图形,不符合题意;
B、既是轴对称图形,又是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意;
故选C.
8.C
本题主要考查了轴对称图形的识别,解题的关键在于能够熟练掌握轴对称图形的定义.
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.根据轴对称图形的定义进行逐一分析判断即可.
解:A、不是轴对称图形,故此选项不符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、是轴对称图形,故此选项符合题意;
D、不是轴对称图形,故此选项不符合题意.
故选:C.
9.B
本题考查的是事件的分类以及不可能事件的含义,根据不可能事件的定义,即在一定条件下必然不会发生的事件,对各选项逐一分析.
解:选项A:投掷硬币可能出现正面或反面,是随机事件,不合题意;
选项B:袋子中仅有红球,无黄球,因此摸出黄球不可能发生,属于不可能事件,符合题意;
选项C:圆无论大小或位置,始终是轴对称图形,属于必然事件,不合题意;
选项D:射击可能命中或脱靶,是随机事件,不合题意;
综上,只有选项B符合不可能事件的定义,
故选:B.
10.C
此题考查了轴对称图形的概念,根据概念逐一判断即可,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称,熟练掌握知识点是解题的关键.
、不是轴对称图形,故本选项不符合题意;
、不是轴对称图形,故本选项不符合题意;
、是轴对称图形,故本选项符合题意;
、不是轴对称图形,故本选项不符合题意;
故选:.
11.C
本题考查了轴对称图形的识别,解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形.
根据轴对称图形的定义即可求解.
解:A、该图形不是轴对称图形,故本选项不符合题意;
B、该图形不是轴对称图形,故本选项不符合题意;
C、该图形是轴对称图形,故本选项符合题意;
D、该图形不是轴对称图形,故本选项不符合题意;
故选:C.
12.D
本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、既是轴对称图形,也是中心对称图形,不符合题意;
B、既是轴对称图形,也是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,不符合题意;
D、既不是轴对称图形,也不是中心对称图形,符合题意;
故选D.
13.A
本题主要考查了中心对称图形和轴对称图形的识别.根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解,把一个图形绕某一点旋转180度,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A、是轴对称图形,不是中心对称图形,故本选项符合题意;
B、是轴对称图形,也是中心对称图形,故本选项不符合题意;
C、是轴对称图形,也是中心对称图形,故本选项不符合题意;
D、是轴对称图形,也是中心对称图形,故本选项不符合题意,
故选:A.
14.A
本题考查了轴对称图形的定义,属于应知应会题型,熟知轴对称图形的概念是关键;
根据轴对称图形的定义:将一个图形沿着某条直线折叠,如果直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,逐项判断即可.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:A.
15.C
本题考查了轴对称图形的识别,解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形.
根据轴对称图形的定义即可求解.
解:根据轴对称图形的定义可得只有“中”字是轴对称图形,符合题意,
故选:C.
16.D
本题考查轴对称图形的识别,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.根据轴对称图形的概念判断即可.
解:A.不是轴对称图形,不合题意;
B.不是轴对称图形,不合题意;
C.不是轴对称图形,不合题意;
D.是轴对称图形,符合题意;
故选:D.
17.B
本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.是轴对称图形,是中心对称图形,符合题意;
C.是轴对称图形,但不是中心对称图形,不符合题意;
D.是轴对称图形,但不是中心对称图形,不符合题意.
故选:B.
18.D
本题考查了轴对称图形的定义,熟知轴对称图形的概念是关键;
根据轴对称图形的定义:如果将一个图形沿着某条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,逐项判定即可得解.
解:A、不能看作是轴对称图形,故本选项不符合题意;
B、不能看作是轴对称图形,故本选项不符合题意;
C、不能看作是轴对称图形,故本选项不符合题意;
D、能看作是轴对称图形,故本选项符合题意;
故选:D.
19.D
本题主要考查了轴对称图形和中心对称图形,根据轴对称图形和中心对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.
解:A、是轴对称图形,不是中心对称图形,故A选项不合题意;
B、是轴对称图形,不是中心对称图形,故B选项不合题意;
C、既不是轴对称图形,也不是中心对称图形,故C选项不合题意;
D、既是轴对称图形又是中心对称图形,故D选项符合题意.
故选:D.
20.B
本题主要考查了轴对称图形的识别,根据轴对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做对称轴.
解:由轴对称图形的定义可知,四个字母中,只有字母“”是轴对称图形,
故选:B.
21.B
本题主要考查了轴对称图形的定义,根据轴对称图形的定义解答即可.如果一个图形沿着某一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.熟练掌握轴对称图形的定义是解题的关键.
解:在四个选项的图形中,只有选项B的图形能找到一条直线,使图形沿这条直线对折后两边能完全重合,故选项B是轴对称图形,选项A、C、D不是轴对称图形.
故选:B.
22.
本题考查了坐标与图形平移变换,解题关键在于掌握左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
根据点的平移规律即可求解.
解:由题意得:将点沿着轴向右平移3个单位,
∴平移后点的坐标为,即,
故答案为:.
23.
本题主要考查了点的平移,掌握平移规律“左减右加,上加下减”是解题的关键.
直接运用平移规律“上加下减”即可解答.
解:将点向下平移2个单位长度,得到的对应点的坐标是,即,
故答案为:.
24.
本题考查平移的性质,掌握平移的不变性是解题的关键.
根据平移的性质可得、,然后求出四边形的周长等于的周长与、的和,再求解即可.
解:沿方向平移个单位长度得到,
,,
四边形的周长
的周长
.
故答案为:.
25.或
本题主要考查折叠的性质,等腰三角形的性质,勾股定理以及相似三角形的判定与性质,分为锐角和钝角两种情况讨论求解:①当为锐角时求出,,由折叠得,可求得,过点作于点,证明,可求出,可求出,根据可得结论;②当为钝角时,过点作于点,得出,可求出,,从而可得.
解:当为锐角时,如图,
根据题意得,
∵,
∴设,则,
∵,
∴,即,解得,
∴,,
由折叠得,
∴;
∴,
过点作于点,则,
∴,
∴,即,
∴
∴,
∴;
当为钝角时,如图,
过点作于点,则,
∴,
同(1)可得,,
∴,
同理可得
∴;
综上所述,的面积为或.
故答案为:或.
26.
本题考查了轴对称的性质,解直角三角形,垂线段最短,熟练掌握轴对称的性质是解题的关键,作点关于的对称点,连接,得出是等腰直角三角形,当时,取得最小值,即周长最小,进而求得,即可求解.
解:如图,作点关于的对称点,连接,
∴周长为,
当四点共线时取得最小值,
∵是关于的对称点,
∴,
又∵
∴
∴是等腰直角三角形,
∴
∴当时,取得最小值,即周长最小
又∵,,
∴
∴周长最小为
故答案为:.
27.6
本题主要考查矩形的性质,旋转的性质以及相似三角形的判定与性质,由矩形的性质得,由勾股定理得,所以,,再证明,可得,设,则,在中由勾股定理得,求出的值即可得到.
解:∵四边形是矩形,
∴;
在中,,
∴,
∵点是的中点,
∴,
由旋转得,,,
∴,
又,
∴,
又,
∴,
∴,
∵,
∴,即,
设,则,
在中,,
∴,
解得(负值舍去),
∴.
故答案为:6.
28.
本题考查了旋转的性质,解直角三角形的相关计算,将线段绕点逆时针旋转得到,过作轴于点,则,,,然后通过,,即可求解,掌握知识点的应用是解题的关键.
解:如图,将线段绕点逆时针旋转得到,过作轴于点,则,
∵点的坐标为,
∴,
由题意得,,,
∴,,
∴点对应点的坐标为,
故答案为:.
29.(1)
(2)抛物线上存在点,使,的坐标为或
(3)的最小值为
本题考查了二次函数的综合应用,待定系数法求二次函数解析式,解直角三角形,轴对称的性质,熟练掌握以上知识是解题的关键;
(1)根据抛物线的对称轴为直线,得出则二次函数解析式为代入,得出,即可求解;
(2)设,根据点的坐标可得,,分量种情况讨论,①当在直线的下方时,以为斜边在的下方作等腰直角三角形,设关于的对称点为,则,验证可得点与点重合,得出,当在的上方时,作点关于的对称点,即,即可求解;
(3)在上取一点,使得,得出,在上取一点,使得,垂足为,则,作关于的对称点,连接交于点,根据轴对称的性质可得当在上时取得最小值,最小值为的长,等面积法求得,则,进而得出,根据,即可求解.
(1)解:∵抛物线的对称轴为直线,
∴,即
∴二次函数解析式为
将代入得,
解得:,
∴二次函数关系式为;
(2)解:在中,当时,解得或,
∴,
当时,,则
∴,,
设,则
①当在直线的下方时,
如图,以为斜边在的下方作等腰直角三角形,
∴,,
设关于的对称点为,则,
∴
∴
∴
∴
又∵
∴点与点重合,
∴
当在的上方时,作点关于的对称点
∵都是等腰直角三角形,
∴在轴上,
综上所述,抛物线上存在点,使,的坐标为或
(3)解:如图,在上取一点,使得
∴
设,则
在中,
∴,即
解得:
∴
∴
∵,
在上取一点,使得,垂足为,
∴
∴
即,
如图,作关于的对称点,连接交于点
∴
∴当在上时取得最小值,最小值为的长,
在中,
∴
∵,
∴
又∵,
∴
∴
∴的最小值为.
30.(1)作图见解析
(2)
(1)以为圆心,为半径画弧,以为圆心,为半径画弧,两弧交于点,连接,即可;
(2)如图,证明,,,,可得,证明,设,则,可得,再解方程即可.
(1)解:如图,即为所求作的三角形;
由作图可得:,,,
∴,
∴即为所求作的三角形;
(2)解:如图,∵矩形,
∴,,,,
∴,
∵,
∴,
∴,
设,则,
∴,
解得:;
∴.
本题考查的是作轴对称图形,全等三角形的判定与性质,矩形的性质,勾股定理的应用,熟练的作图是解本题的关键.
31.(1)见解析;(2)4;(3)
(1)由折叠的性质得:,再结合平行四边形的性质可得,然后根据三角形内角和定理可得,即可求证;
(2)根据全等三角形的性质可得,从而得到,可证明,从而得到,再由折叠的性质得:,再根据,可得,即可求解;
(3)延长交于点,设,,证明得出,证明得出,证明得出,进而求得,根据得出,根据相似三角形的性质,即可求解.
解:(1)由折叠的性质得:,
∵四边形是平行四边形,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又∵,
∴;
(2)∵,
∴,
∵,
∴,
∵,,
∴,
∴,
由折叠的性质得:,
∵四边形是平行四边形,
∴,,
∴,
∴,
∴,解得:,
∴,
∴;
(3)解:如图,延长交于点,
设,
∵,
∴,,
∴,
∵折叠,
∴
∵,即
∴
∴即
∴
∵四边形是平行四边形,
∴
又∵折叠,
∴
∵
∴
∴
∵
∴
∵
∴
∴
又∵
∴
∴即
∴
∵
∴
∴
∴
解得:
∴
又∵
∴
∴.
本题考查了平行四边形的性质,全等三角形的性质与判定,相似三角形的性质与判定,折叠的性质,熟练掌握以上知识是解题的关键.
32.(1)直吊臂的长为10米
(2)上升了5米
本题考查了解直角三角形的实际应用,旋转的性质,矩形的性质与判定,正确理解题意,构造直角三角形是解题的关键.
(1)根据,即可解,即可求解;
(2)记旋转后的点的对应点为,延长交于点,过点作于点,可得四边形为矩形,则米,在中,由求出,再由,即可求解.
(1)解:由题意得,,
∵,米,
∴在中,(米),
答:直吊臂的长为10米;
(2)解:记旋转后的点的对应点为,延长交于点,过点作于点,则,
由题意得:米,米,
∴,
∴四边形为矩形,
∴米,
在中,米,
∴(米),
∴货物上升了5米.
33.探究发现:,;实践应用:;拓展延伸:
探究发现:图形面积分割法得出,根据得出;
实践应用:过点分别作的垂线,垂足分别为,根据等边三角形的性质,含度角的直角三角形的性质,勾股定理分别求得,,进而根据旋转的性质可得是等边三角形,同理求得的长,进而根据探究发现的结论,即可求解;
拓展延伸:延长交于点,过点作于点,设,根据圆周角定理,得出,在,中,根据勾股定理,求得,进而根据弧与圆周角的关系,得出,根据前面的结论,即可求解.
解:探究发现:∵,,
∴,
∴,
∵,
∴;
故答案为:,,;.
实践应用:如图,过点分别作的垂线,垂足分别为,
∵是等边三角形,,
∴,
∵,
∴,,
∴,
∵,则,
∴,
在中,.
∵将线段绕点逆时针旋转得,
∴
∴是等边三角形,
∴,则,
∴由探究发现可得:.
拓展延伸:如图,延长交于点,过点作于点,连接,
设,
∵是半圆的直径,
∴,
∵,
在中,,
在中,,
∴,
解得:,
∴,
∴,
∴,
∴,
∴.
∴由探究发现可得:,
∵,
∴,
∵,
∴
.
本题考查了勾股定理,点到直线的距离,等腰三角形的性质与判定,等边三角形的性质与判定,旋转的性质,含30度角的直角三角形的性质,弧与圆周角的关系,熟练掌握等面积法求线段长是解题的关键.
一、单选题
1.(2025·湖南·中考真题)在平面直角坐标系中,将点向右平移个单位长度到处,则点的坐标为( )
A. B. C. D.
2.(2025·四川自贡·中考真题)如图,在平面直角坐标系中,将平移,得到,点在坐标轴上.若,则点坐标为( )
A. B. C. D.
3.(2025·四川眉山·中考真题)在平面直角坐标系中,将点向右平移2个单位到点B,则点B的坐标为( )
A. B. C. D.
4.(2025·黑龙江绥化·中考真题)下列数学符号是轴对称图形的是( )
A. B. C. D.
5.(2025·黑龙江·中考真题)我国古代有很多关于数学的伟大发现,其中包括很多美丽的图案,下列图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.(2025·天津·中考真题)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
7.(2025·江苏扬州·中考真题)窗棂是中国传统木构建筑的重要元素,既散发着古典之韵,又展现了几何之美.下列窗棂图案中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
8.(2025·湖南·中考真题)武术是我国传统的体育项目.下列武术动作图形中,是轴对称图形的是( )
A. B. C. D.
9.(2025·湖北·中考真题)在下列事件中,不可能事件是( )
A.投掷一枚硬币,正面向上 B.从只有红球的袋子中摸出黄球
C.任意画一个圆,它是轴对称图形 D.射击运动员射击一次,命中靶心
10.(2025·新疆·中考真题)下列四种化学仪器的示意图中,是轴对称图形的是( )
A. B. C. D.
11.(2025·四川泸州·中考真题)下列人工智能助手图标中,是轴对称图形的是( )
A. B. C. D.
12.(2025·福建·中考真题)中国古算诗词歌赋较多.古算诗词题,是反映数学数量关系的内在联系及其规律的一种文学浪漫形式.下列分别是古算诗词题“圆中方形”“方形圆径”“圆材藏壁”“勾股容圆”所描绘的图形,其中既不是轴对称图形也不是中心对称图形的是( )
A. B. C. D.
13.(2025·江西·中考真题)下列图案中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
14.(2025·四川眉山·中考真题)剪纸是我国传统的民间艺术.下列剪纸作品中属于轴对称图形的是( )
A. B. C. D.
15.(2025·云南·中考真题)中华文明,源远流长;中华汉字,寓意深广,下列四个选项中,是轴对称图形的为( )
A. B. C. D.
16.(2025·四川广安·中考真题)下列实验仪器的平面示意图中,是轴对称图形的是( )
A. B. C. D.
17.(2025·山东·中考真题)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
18.(2025·四川遂宁·中考真题)汉字作为中华优秀传统文化的根脉和重要载体,在发展过程中演变出多种字体,给人以美的享受.下面是“遂宁之美”四个字的篆书,能看作是轴对称图形的是( )
A. B. C. D.
19.(2025·四川内江·中考真题)古钱币是我国珍贵的历史文化遗产.下列选项是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
20.(2025·四川凉山·中考真题)以下字母是轴对称图形的是( )
A. B. C. D.
21.(2025·重庆·中考真题)下列图案中,是轴对称图形的是( )
A. B. C. D.
二、填空题
22.(2025·广东深圳·中考真题)如图,将无人机沿着轴向右平移3个单位,若无人机上一点的坐标为,则平移后点的坐标为 .
23.(2025·山东·中考真题)在平面直角坐标系中,将点向下平移2个单位长度,得到的对应点的坐标是 .
24.(2025·四川凉山·中考真题)如图,将周长为20的沿方向平移2个单位长度得,连接,则四边形的周长为 .
25.(2025·黑龙江齐齐哈尔·中考真题)等腰三角形纸片中,,将纸片沿直线l折叠,使点A与点B重合,直线l交于点D,交直线于点E,连接,若,,则的面积为 .
26.(2025·四川内江·中考真题)如图,在中,,,,点、、分别是边、、上的动点,则周长的最小值是 .
27.(2025·广东深圳·中考真题)如图,以矩形的点为圆心,的长为半径作,交于点,点为上一点,连接,将线段绕点顺时针旋转至,点落在上,且点为中点.若,,则的长为 .
28.(2025·山西·中考真题)如图,在平面直角坐标系中,点的坐标为,将线段绕点逆时针旋转,则点对应点的坐标为 .
三、解答题
29.(2025·四川遂宁·中考真题)如图,在平面直角坐标系中,二次函数(为常数)的图像与轴交于、两点,交轴于点,对称轴为直线.
(1)求二次函数关系式.
(2)连接,抛物线上是否存在点,使,若存在,求出点的坐标,若不存在,说明理由.
(3)在轴上方的抛物线上找一点,作射线,使,点是线段上的一动点,过点作轴,垂足为点,连结,求的最小值.
30.(2025·山东烟台·中考真题)如图,是矩形的对角线,请按以下要求解决问题:
(1)利用尺规作,使与关于直线成轴对称(不写作法,保留作图痕迹);
(2)在(1)的条件下,若交于点,,,求的长.
31.(2025·四川成都·中考真题)如图,在中,点在边上,点关于直线的对称点落在内,射线交射线于点,交射线于点,射线交边于点.
【特例感知】
(1)如图1,当时,点在延长线上,求证:;
【问题探究】
(2)在(1)的条件下,若,,求的长;
【拓展延伸】
(3)如图2,当时,点在边上,若,求的值.(用含的代数式表示)
32.(2025·四川凉山·中考真题)某型号起重机吊起一货物M在空中保持静止状态时,如图1,货物M与点O的连线恰好平行于地面,米,.(参考数据:,结果精确到1米)
(1)求直吊臂的长;
(2)如图2,直吊臂与的长度保持不变,绕点O逆时针旋转,当时,货物M上升了多少米?
33.(2025·四川达州·中考真题)综合与实践
问题提出:探究图形中线段之间的数量关系,通常将一个图形分割成几个图形,根据面积不变,获得线段之间的数量关系.
探究发现:如图1,在中,,是边上一点,过点作于,于,过点作于.连结,由图形面积分割法得:______;则____________.
实践应用:如图2,是等边三角形,,点是边上一点,连结.将线段绕点逆时针旋转得,连结交于,过点作于,于,当时,求的值.
拓展延伸:如图3,已知是半圆的直径,,是弦,,是上一点,,垂足为,,求的值.
《专题25 图形的平移翻折对称(33题)-2025年中考数学真题分类汇编(全国通用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D B B C C B C
题号 11 12 13 14 15 16 17 18 19 20
答案 C D A A C D B D D B
题号 21
答案 B
1.B
本题主要考查点的平移,掌握平移规律是关键.
根据平面直角坐标系中点的平移规律,向右平移时横坐标增加,纵坐标不变,即可解题.
解:点向右平移3个单位长度,横坐标需加3,即,纵坐标2保持不变,
∴平移后的点坐标为,
故选:B.
2.B
本题考查解直角三角形,相似三角形的判定和性质,坐标与图形变换—平移,熟练掌握相关知识点,添加辅助线构造相似三角形,是解题的关键.过点作轴,作交的延长线于点,证明,得到,根据点的坐标,结合的值,求出,平移求出点坐标,进而得到平移规则,再求出点坐标即可.
解:过点作轴,作交的延长线于点,则:
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵平移,
∴,
∴,
∴将点先向右平移10个单位,再向下平移3个单位得到点,
∴将点先向右平移10个单位,再向下平移3个单位得到点,
∴;
故选B.
3.C
本题主要考查了坐标与图形变化﹣平移.掌握平移的规律“左右横,上下纵,正加负减”是解答本题的关键.
根据平移规律,向右平移2个单位时,点的横坐标增加2,纵坐标不变,即可解答.
解:点向右平移2个单位,横坐标变为,纵坐标保持3不变.
所以,点的坐标为,、
故选:C.
4.D
本题考查了轴对称图形的定义,熟知轴对称图形的概念是解题的关键;
根据轴对称图形的定义:如果将一个图形沿着某条直线折叠,直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,即可解答.
解: 选项中的数学符号是轴对称图形的是,其它的都不是;
故选:D.
5.B
本题考查了中心对称图形和轴对称图形的定义,能熟记中心对称图形和轴对称图形的定义是解此题的关键.中心对称图形是在平面内,把一个图形绕某一定点旋转,能够与自身重合的图形;轴对称图形是在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.依据定义判断即可.
解:A中、是轴对称图形,不是中心对称图形,不符合题意;
B中、既是轴对称图形,又是中心对称图形,符合题意;
C中、是中心对称图形,不是轴对称图形,不符合题意;
D中、既不是轴对称图形,也不是中心对称图形,不符合题意;
故选:B.
6.B
本题主要查了轴对称图形.根据轴对称图形得定义,逐项判断,即可求解.
解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:B
7.C
本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、既是轴对称图形,又是中心对称图形,不符合题意;
B、既是轴对称图形,又是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意;
故选C.
8.C
本题主要考查了轴对称图形的识别,解题的关键在于能够熟练掌握轴对称图形的定义.
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.根据轴对称图形的定义进行逐一分析判断即可.
解:A、不是轴对称图形,故此选项不符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、是轴对称图形,故此选项符合题意;
D、不是轴对称图形,故此选项不符合题意.
故选:C.
9.B
本题考查的是事件的分类以及不可能事件的含义,根据不可能事件的定义,即在一定条件下必然不会发生的事件,对各选项逐一分析.
解:选项A:投掷硬币可能出现正面或反面,是随机事件,不合题意;
选项B:袋子中仅有红球,无黄球,因此摸出黄球不可能发生,属于不可能事件,符合题意;
选项C:圆无论大小或位置,始终是轴对称图形,属于必然事件,不合题意;
选项D:射击可能命中或脱靶,是随机事件,不合题意;
综上,只有选项B符合不可能事件的定义,
故选:B.
10.C
此题考查了轴对称图形的概念,根据概念逐一判断即可,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称,熟练掌握知识点是解题的关键.
、不是轴对称图形,故本选项不符合题意;
、不是轴对称图形,故本选项不符合题意;
、是轴对称图形,故本选项符合题意;
、不是轴对称图形,故本选项不符合题意;
故选:.
11.C
本题考查了轴对称图形的识别,解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形.
根据轴对称图形的定义即可求解.
解:A、该图形不是轴对称图形,故本选项不符合题意;
B、该图形不是轴对称图形,故本选项不符合题意;
C、该图形是轴对称图形,故本选项符合题意;
D、该图形不是轴对称图形,故本选项不符合题意;
故选:C.
12.D
本题考查了轴对称图形,中心对称图形的识别.解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180度,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.根据中心对称和轴对称的定义,进行判断即可.
解:A、既是轴对称图形,也是中心对称图形,不符合题意;
B、既是轴对称图形,也是中心对称图形,不符合题意;
C、是轴对称图形,不是中心对称图形,不符合题意;
D、既不是轴对称图形,也不是中心对称图形,符合题意;
故选D.
13.A
本题主要考查了中心对称图形和轴对称图形的识别.根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解,把一个图形绕某一点旋转180度,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A、是轴对称图形,不是中心对称图形,故本选项符合题意;
B、是轴对称图形,也是中心对称图形,故本选项不符合题意;
C、是轴对称图形,也是中心对称图形,故本选项不符合题意;
D、是轴对称图形,也是中心对称图形,故本选项不符合题意,
故选:A.
14.A
本题考查了轴对称图形的定义,属于应知应会题型,熟知轴对称图形的概念是关键;
根据轴对称图形的定义:将一个图形沿着某条直线折叠,如果直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,逐项判断即可.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:A.
15.C
本题考查了轴对称图形的识别,解题的关键在于熟练掌握:在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形.
根据轴对称图形的定义即可求解.
解:根据轴对称图形的定义可得只有“中”字是轴对称图形,符合题意,
故选:C.
16.D
本题考查轴对称图形的识别,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.根据轴对称图形的概念判断即可.
解:A.不是轴对称图形,不合题意;
B.不是轴对称图形,不合题意;
C.不是轴对称图形,不合题意;
D.是轴对称图形,符合题意;
故选:D.
17.B
本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.是轴对称图形,是中心对称图形,符合题意;
C.是轴对称图形,但不是中心对称图形,不符合题意;
D.是轴对称图形,但不是中心对称图形,不符合题意.
故选:B.
18.D
本题考查了轴对称图形的定义,熟知轴对称图形的概念是关键;
根据轴对称图形的定义:如果将一个图形沿着某条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,逐项判定即可得解.
解:A、不能看作是轴对称图形,故本选项不符合题意;
B、不能看作是轴对称图形,故本选项不符合题意;
C、不能看作是轴对称图形,故本选项不符合题意;
D、能看作是轴对称图形,故本选项符合题意;
故选:D.
19.D
本题主要考查了轴对称图形和中心对称图形,根据轴对称图形和中心对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.
解:A、是轴对称图形,不是中心对称图形,故A选项不合题意;
B、是轴对称图形,不是中心对称图形,故B选项不合题意;
C、既不是轴对称图形,也不是中心对称图形,故C选项不合题意;
D、既是轴对称图形又是中心对称图形,故D选项符合题意.
故选:D.
20.B
本题主要考查了轴对称图形的识别,根据轴对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做对称轴.
解:由轴对称图形的定义可知,四个字母中,只有字母“”是轴对称图形,
故选:B.
21.B
本题主要考查了轴对称图形的定义,根据轴对称图形的定义解答即可.如果一个图形沿着某一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.熟练掌握轴对称图形的定义是解题的关键.
解:在四个选项的图形中,只有选项B的图形能找到一条直线,使图形沿这条直线对折后两边能完全重合,故选项B是轴对称图形,选项A、C、D不是轴对称图形.
故选:B.
22.
本题考查了坐标与图形平移变换,解题关键在于掌握左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
根据点的平移规律即可求解.
解:由题意得:将点沿着轴向右平移3个单位,
∴平移后点的坐标为,即,
故答案为:.
23.
本题主要考查了点的平移,掌握平移规律“左减右加,上加下减”是解题的关键.
直接运用平移规律“上加下减”即可解答.
解:将点向下平移2个单位长度,得到的对应点的坐标是,即,
故答案为:.
24.
本题考查平移的性质,掌握平移的不变性是解题的关键.
根据平移的性质可得、,然后求出四边形的周长等于的周长与、的和,再求解即可.
解:沿方向平移个单位长度得到,
,,
四边形的周长
的周长
.
故答案为:.
25.或
本题主要考查折叠的性质,等腰三角形的性质,勾股定理以及相似三角形的判定与性质,分为锐角和钝角两种情况讨论求解:①当为锐角时求出,,由折叠得,可求得,过点作于点,证明,可求出,可求出,根据可得结论;②当为钝角时,过点作于点,得出,可求出,,从而可得.
解:当为锐角时,如图,
根据题意得,
∵,
∴设,则,
∵,
∴,即,解得,
∴,,
由折叠得,
∴;
∴,
过点作于点,则,
∴,
∴,即,
∴
∴,
∴;
当为钝角时,如图,
过点作于点,则,
∴,
同(1)可得,,
∴,
同理可得
∴;
综上所述,的面积为或.
故答案为:或.
26.
本题考查了轴对称的性质,解直角三角形,垂线段最短,熟练掌握轴对称的性质是解题的关键,作点关于的对称点,连接,得出是等腰直角三角形,当时,取得最小值,即周长最小,进而求得,即可求解.
解:如图,作点关于的对称点,连接,
∴周长为,
当四点共线时取得最小值,
∵是关于的对称点,
∴,
又∵
∴
∴是等腰直角三角形,
∴
∴当时,取得最小值,即周长最小
又∵,,
∴
∴周长最小为
故答案为:.
27.6
本题主要考查矩形的性质,旋转的性质以及相似三角形的判定与性质,由矩形的性质得,由勾股定理得,所以,,再证明,可得,设,则,在中由勾股定理得,求出的值即可得到.
解:∵四边形是矩形,
∴;
在中,,
∴,
∵点是的中点,
∴,
由旋转得,,,
∴,
又,
∴,
又,
∴,
∴,
∵,
∴,即,
设,则,
在中,,
∴,
解得(负值舍去),
∴.
故答案为:6.
28.
本题考查了旋转的性质,解直角三角形的相关计算,将线段绕点逆时针旋转得到,过作轴于点,则,,,然后通过,,即可求解,掌握知识点的应用是解题的关键.
解:如图,将线段绕点逆时针旋转得到,过作轴于点,则,
∵点的坐标为,
∴,
由题意得,,,
∴,,
∴点对应点的坐标为,
故答案为:.
29.(1)
(2)抛物线上存在点,使,的坐标为或
(3)的最小值为
本题考查了二次函数的综合应用,待定系数法求二次函数解析式,解直角三角形,轴对称的性质,熟练掌握以上知识是解题的关键;
(1)根据抛物线的对称轴为直线,得出则二次函数解析式为代入,得出,即可求解;
(2)设,根据点的坐标可得,,分量种情况讨论,①当在直线的下方时,以为斜边在的下方作等腰直角三角形,设关于的对称点为,则,验证可得点与点重合,得出,当在的上方时,作点关于的对称点,即,即可求解;
(3)在上取一点,使得,得出,在上取一点,使得,垂足为,则,作关于的对称点,连接交于点,根据轴对称的性质可得当在上时取得最小值,最小值为的长,等面积法求得,则,进而得出,根据,即可求解.
(1)解:∵抛物线的对称轴为直线,
∴,即
∴二次函数解析式为
将代入得,
解得:,
∴二次函数关系式为;
(2)解:在中,当时,解得或,
∴,
当时,,则
∴,,
设,则
①当在直线的下方时,
如图,以为斜边在的下方作等腰直角三角形,
∴,,
设关于的对称点为,则,
∴
∴
∴
∴
又∵
∴点与点重合,
∴
当在的上方时,作点关于的对称点
∵都是等腰直角三角形,
∴在轴上,
综上所述,抛物线上存在点,使,的坐标为或
(3)解:如图,在上取一点,使得
∴
设,则
在中,
∴,即
解得:
∴
∴
∵,
在上取一点,使得,垂足为,
∴
∴
即,
如图,作关于的对称点,连接交于点
∴
∴当在上时取得最小值,最小值为的长,
在中,
∴
∵,
∴
又∵,
∴
∴
∴的最小值为.
30.(1)作图见解析
(2)
(1)以为圆心,为半径画弧,以为圆心,为半径画弧,两弧交于点,连接,即可;
(2)如图,证明,,,,可得,证明,设,则,可得,再解方程即可.
(1)解:如图,即为所求作的三角形;
由作图可得:,,,
∴,
∴即为所求作的三角形;
(2)解:如图,∵矩形,
∴,,,,
∴,
∵,
∴,
∴,
设,则,
∴,
解得:;
∴.
本题考查的是作轴对称图形,全等三角形的判定与性质,矩形的性质,勾股定理的应用,熟练的作图是解本题的关键.
31.(1)见解析;(2)4;(3)
(1)由折叠的性质得:,再结合平行四边形的性质可得,然后根据三角形内角和定理可得,即可求证;
(2)根据全等三角形的性质可得,从而得到,可证明,从而得到,再由折叠的性质得:,再根据,可得,即可求解;
(3)延长交于点,设,,证明得出,证明得出,证明得出,进而求得,根据得出,根据相似三角形的性质,即可求解.
解:(1)由折叠的性质得:,
∵四边形是平行四边形,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又∵,
∴;
(2)∵,
∴,
∵,
∴,
∵,,
∴,
∴,
由折叠的性质得:,
∵四边形是平行四边形,
∴,,
∴,
∴,
∴,解得:,
∴,
∴;
(3)解:如图,延长交于点,
设,
∵,
∴,,
∴,
∵折叠,
∴
∵,即
∴
∴即
∴
∵四边形是平行四边形,
∴
又∵折叠,
∴
∵
∴
∴
∵
∴
∵
∴
∴
又∵
∴
∴即
∴
∵
∴
∴
∴
解得:
∴
又∵
∴
∴.
本题考查了平行四边形的性质,全等三角形的性质与判定,相似三角形的性质与判定,折叠的性质,熟练掌握以上知识是解题的关键.
32.(1)直吊臂的长为10米
(2)上升了5米
本题考查了解直角三角形的实际应用,旋转的性质,矩形的性质与判定,正确理解题意,构造直角三角形是解题的关键.
(1)根据,即可解,即可求解;
(2)记旋转后的点的对应点为,延长交于点,过点作于点,可得四边形为矩形,则米,在中,由求出,再由,即可求解.
(1)解:由题意得,,
∵,米,
∴在中,(米),
答:直吊臂的长为10米;
(2)解:记旋转后的点的对应点为,延长交于点,过点作于点,则,
由题意得:米,米,
∴,
∴四边形为矩形,
∴米,
在中,米,
∴(米),
∴货物上升了5米.
33.探究发现:,;实践应用:;拓展延伸:
探究发现:图形面积分割法得出,根据得出;
实践应用:过点分别作的垂线,垂足分别为,根据等边三角形的性质,含度角的直角三角形的性质,勾股定理分别求得,,进而根据旋转的性质可得是等边三角形,同理求得的长,进而根据探究发现的结论,即可求解;
拓展延伸:延长交于点,过点作于点,设,根据圆周角定理,得出,在,中,根据勾股定理,求得,进而根据弧与圆周角的关系,得出,根据前面的结论,即可求解.
解:探究发现:∵,,
∴,
∴,
∵,
∴;
故答案为:,,;.
实践应用:如图,过点分别作的垂线,垂足分别为,
∵是等边三角形,,
∴,
∵,
∴,,
∴,
∵,则,
∴,
在中,.
∵将线段绕点逆时针旋转得,
∴
∴是等边三角形,
∴,则,
∴由探究发现可得:.
拓展延伸:如图,延长交于点,过点作于点,连接,
设,
∵是半圆的直径,
∴,
∵,
在中,,
在中,,
∴,
解得:,
∴,
∴,
∴,
∴,
∴.
∴由探究发现可得:,
∵,
∴,
∵,
∴
.
本题考查了勾股定理,点到直线的距离,等腰三角形的性质与判定,等边三角形的性质与判定,旋转的性质,含30度角的直角三角形的性质,弧与圆周角的关系,熟练掌握等面积法求线段长是解题的关键.
同课章节目录
