5.2.1实际问题的函数刻画 课件(共19张PPT) (北师大版2019必修第一册)
文档属性
| 名称 | 5.2.1实际问题的函数刻画 课件(共19张PPT) (北师大版2019必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 16:23:53 | ||
图片预览






文档简介
(共19张PPT)
5.2.1
实际问题的函数刻画
新课导入
典例剖析
例1 某公司设计了一种新型的几何模板.经测算每件产品的直接成本是130元,市场的合适售价是 190元.另外,还投人了15 万元用于研发.显然,这家公司一方面要尽力为使用者提供可信的产品,另一方面又要争取获得好的收益.当这种新型几何模板畅销时,怎样计算总收益呢 (销售仓储及维护等环节成本忽略不计)
典例剖析
(1)首先看这个问题涉及的几个因素:
①生产总成本(记作 C元)与产量及单件产品的直接成本、研发费用有关系;
②销售总收(记作 R元)与销售量及销售单价有关系;
③总收益(记作 L元)与生产总成本及销售总收有关系.
其中,销售单价、单件产品的直接成本和研发费用都是定量;当产品畅销时,销售量等于产量,产量是变量,可以设为x件.
解析
典例剖析
(2)再来看上述各因素之间满足的关系:
①生产总成本C与产量x的关系为C=150 000+130x;
②销售总收入R与产量的关系为R=190x;
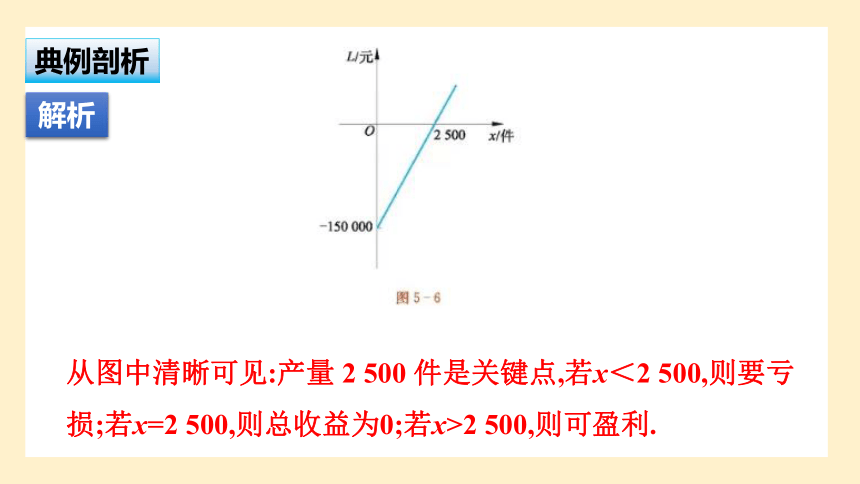
③总收益L与产量x的关系为L=R-C=60x-150 000(x≥0).
L关于x的函数图象如图 5-6.
解析
典例剖析
从图中清晰可见:产量 2 500 件是关键点,若x<2 500,则要亏损;若x=2 500,则总收益为0;若x>2 500,则可盈利.
解析
典例剖析
典例剖析
典例剖析
(1)观察表5-2,设脚长(新鞋码)、鞋号(旧鞋码)分别为x,y,将每一对数x,y对应的数对(x,y)用平面直角坐系的点来表示(如图5-7).
解析
可以看出,这些点都在一条直线上,不妨设这条直线为y=kx+b.利用表中任意两组数,
得k=0.2,b=-10.
所以y=0.2x-10.
这就是鞋号关于脚长的函数模型.
典例剖析
解析
(2)当 y=30时,x=200,即能穿 30 号鞋的女童的脚长不超过200 mm.
(3)当x=262时,y=42.4,即脚长为 262 mm 的女篮球运动员应穿 43 号的鞋.
典例剖析
解析
例3 现有一把椅子,四条腿一样长且四脚连线成正方形,需放在起伏不平但光滑的地面上,问能否将这把椅子四脚同时落地放稳
如图5-8,记这把椅子四脚连线所形成的图形为正方形ABCD,对角线的交点为 O;以点O为旋转中心,初始位置的AC转过角时,记A,C两点与地面距离之和为f (),B,D两点与地面距离之和为 g任意位置的椅子都可以三只脚与地面接触,所以总有 f()·g()=0.记 F()=f()-g(),显然函数 F()的图象是不间断的曲线.
典例剖析
解析
对于初始位置,不妨设 f(0°)=0,g(0°) >0,那么
F(0°)=-g(0°)≤0,椅子旋转 90°,点D转到点A,
g(90°)=f(0°)=0,f(90°)=g(0)≥0,那么F(90°)=f(90°) ≥ 0.
于是,根据函数零点存在定理,可知在区间[0°,90°]上存在a,使得 F(a)=0即f(a)=g(a)=0,所以这把椅子四脚能够同时落地放稳.
典例剖析
解析
例4 加油站的汽油都存储在地下油槽中,由于比较容易测量槽中油料的高度,因此一般用油料的高度来监控油槽中的油料量.现有一圆柱油槽,横卧地下,其母线呈水平状态,纵截面是圆(如图 5-9),截面圆半径是120cm,圆柱的长是400 cm.从资料可查出圆的形面积与圆面积比例系数表(如表 5-3),它给出了形面积占形所在圆面积的比值 C(k).
其中
典例剖析
为了方便加油站操作人员估计油槽中的油料量,请编制一份油料的液面高度 h(单位:cm)与油料量 V(单位:L)的对照表该表的油料液面高度取值从0开始,最大为 120 cm,间隔12 cm.( π取 3.14,油料量精确到 1 L)
典例剖析
如图5-9,油槽截面的油料液面线为AB,油料液面高度时的油料的面为S(h)依题意知
典例剖析
解析
典例剖析
解析
V(h)=400S(h).
这里r=120 cm,于是可得到油料的液面高度h 与油料量V的对照表(如表5-4).
实际问题的数学刻画
(1)认真读题,慎密审题.
(2)引进数学符号,建立数学模型.
(3)会用数学结果诠释实际问题,用数学的眼光看待实际问题.
课堂小结
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
5.2.1
实际问题的函数刻画
新课导入
典例剖析
例1 某公司设计了一种新型的几何模板.经测算每件产品的直接成本是130元,市场的合适售价是 190元.另外,还投人了15 万元用于研发.显然,这家公司一方面要尽力为使用者提供可信的产品,另一方面又要争取获得好的收益.当这种新型几何模板畅销时,怎样计算总收益呢 (销售仓储及维护等环节成本忽略不计)
典例剖析
(1)首先看这个问题涉及的几个因素:
①生产总成本(记作 C元)与产量及单件产品的直接成本、研发费用有关系;
②销售总收(记作 R元)与销售量及销售单价有关系;
③总收益(记作 L元)与生产总成本及销售总收有关系.
其中,销售单价、单件产品的直接成本和研发费用都是定量;当产品畅销时,销售量等于产量,产量是变量,可以设为x件.
解析
典例剖析
(2)再来看上述各因素之间满足的关系:
①生产总成本C与产量x的关系为C=150 000+130x;
②销售总收入R与产量的关系为R=190x;
③总收益L与产量x的关系为L=R-C=60x-150 000(x≥0).
L关于x的函数图象如图 5-6.
解析
典例剖析
从图中清晰可见:产量 2 500 件是关键点,若x<2 500,则要亏损;若x=2 500,则总收益为0;若x>2 500,则可盈利.
解析
典例剖析
典例剖析
典例剖析
(1)观察表5-2,设脚长(新鞋码)、鞋号(旧鞋码)分别为x,y,将每一对数x,y对应的数对(x,y)用平面直角坐系的点来表示(如图5-7).
解析
可以看出,这些点都在一条直线上,不妨设这条直线为y=kx+b.利用表中任意两组数,
得k=0.2,b=-10.
所以y=0.2x-10.
这就是鞋号关于脚长的函数模型.
典例剖析
解析
(2)当 y=30时,x=200,即能穿 30 号鞋的女童的脚长不超过200 mm.
(3)当x=262时,y=42.4,即脚长为 262 mm 的女篮球运动员应穿 43 号的鞋.
典例剖析
解析
例3 现有一把椅子,四条腿一样长且四脚连线成正方形,需放在起伏不平但光滑的地面上,问能否将这把椅子四脚同时落地放稳
如图5-8,记这把椅子四脚连线所形成的图形为正方形ABCD,对角线的交点为 O;以点O为旋转中心,初始位置的AC转过角时,记A,C两点与地面距离之和为f (),B,D两点与地面距离之和为 g任意位置的椅子都可以三只脚与地面接触,所以总有 f()·g()=0.记 F()=f()-g(),显然函数 F()的图象是不间断的曲线.
典例剖析
解析
对于初始位置,不妨设 f(0°)=0,g(0°) >0,那么
F(0°)=-g(0°)≤0,椅子旋转 90°,点D转到点A,
g(90°)=f(0°)=0,f(90°)=g(0)≥0,那么F(90°)=f(90°) ≥ 0.
于是,根据函数零点存在定理,可知在区间[0°,90°]上存在a,使得 F(a)=0即f(a)=g(a)=0,所以这把椅子四脚能够同时落地放稳.
典例剖析
解析
例4 加油站的汽油都存储在地下油槽中,由于比较容易测量槽中油料的高度,因此一般用油料的高度来监控油槽中的油料量.现有一圆柱油槽,横卧地下,其母线呈水平状态,纵截面是圆(如图 5-9),截面圆半径是120cm,圆柱的长是400 cm.从资料可查出圆的形面积与圆面积比例系数表(如表 5-3),它给出了形面积占形所在圆面积的比值 C(k).
其中
典例剖析
为了方便加油站操作人员估计油槽中的油料量,请编制一份油料的液面高度 h(单位:cm)与油料量 V(单位:L)的对照表该表的油料液面高度取值从0开始,最大为 120 cm,间隔12 cm.( π取 3.14,油料量精确到 1 L)
典例剖析
如图5-9,油槽截面的油料液面线为AB,油料液面高度时的油料的面为S(h)依题意知
典例剖析
解析
典例剖析
解析
V(h)=400S(h).
这里r=120 cm,于是可得到油料的液面高度h 与油料量V的对照表(如表5-4).
实际问题的数学刻画
(1)认真读题,慎密审题.
(2)引进数学符号,建立数学模型.
(3)会用数学结果诠释实际问题,用数学的眼光看待实际问题.
课堂小结
谢谢您的聆听
Copy paste fonts. Choose the only option to retain text……
Copy paste fonts. Choose the only
option to retain text……
THANKS
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
