第七单元解决问题的策略暑假预习练(含解析) 苏教版数学五年级上册
文档属性
| 名称 | 第七单元解决问题的策略暑假预习练(含解析) 苏教版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 383.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 12:13:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第七单元解决问题的策略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.将7个点连成线段,任意三点不在同一条直线上,最多可以连成( )。
A.7条 B.12条 C.21条 D.28条
2.用下面2个偏旁和4个汉字,一共可以组成( )个新的汉字。
A.4 B.6 C.8 D.10
3.六年级8个班进行男子三人制篮球赛,如果首轮(8进4)进行淘汰赛,次轮进行循环赛,最后产生冠军,一共要比赛( )场。
A.7 B.8 C.9 D.10
4.小欣一家三口到影楼照全家福,摄影师有( )种排列方法。
A.3 B.1 C.6
5.如图,小蚂蚁从点A爬到点B,走最短的路线,共有( )种不同的路线。
A.6 B.8 C.10 D.12
6.用写有0、3、4、5的四张数字卡片,能摆出( )不同的三位数。
A.6个 B.12个 C.16个 D.18个
7.有1元、2元、5元和10元人民币各1张,任意取2张,可以有( )种不同的取法。
A.4 B.6 C.10 D.14
8.次央今年8岁,爸爸今年40岁,再过( )年,爸爸的年龄是次央年龄的3倍。
A.4 B.6 C.8 D.10
9.用形如的框每次框下表中的两个数,共有得到( )种不同的和。
A.62 B.63 C.64 D.65
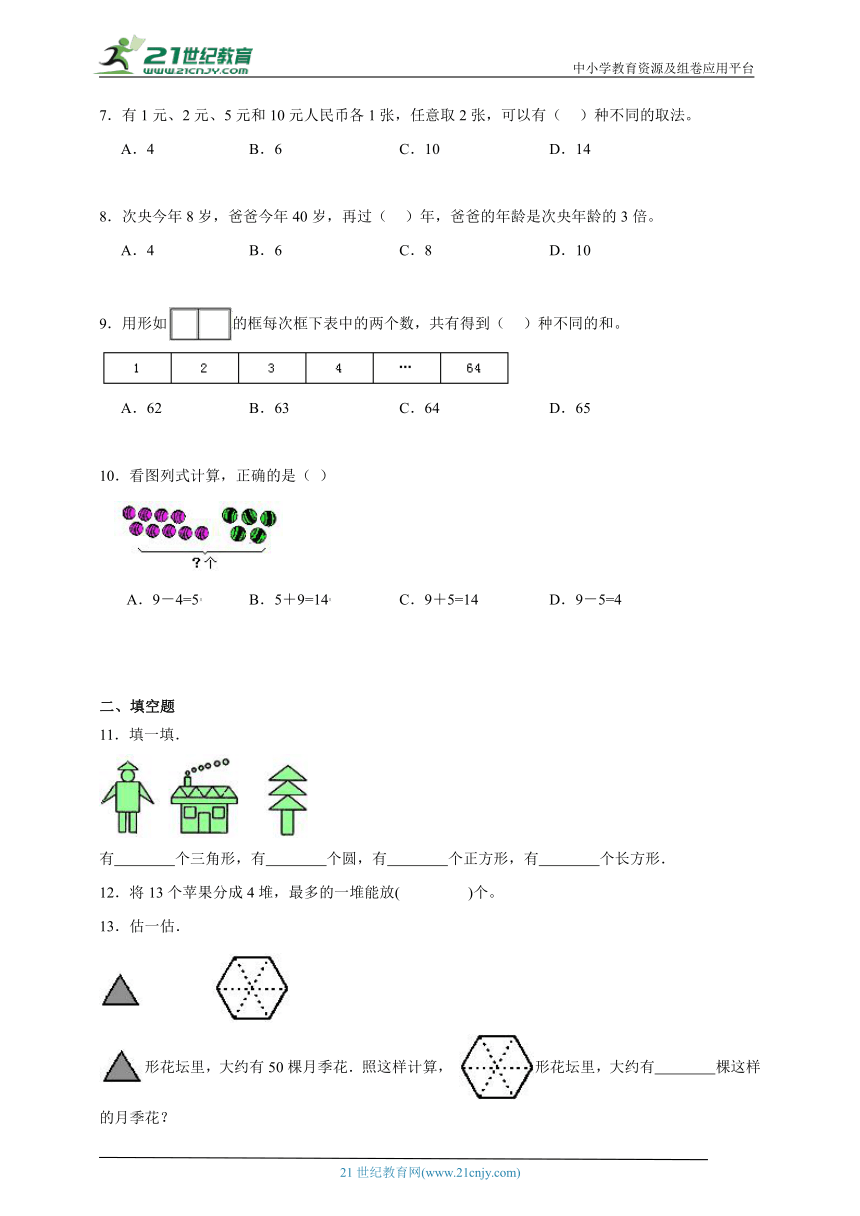
10.看图列式计算,正确的是( )
A.9-4=5 B.5+9=14 C.9+5=14 D.9-5=4
二、填空题
11.填一填.
有 个三角形,有 个圆,有 个正方形,有 个长方形.
12.将13个苹果分成4堆,最多的一堆能放( )个。
13.估一估.
形花坛里,大约有50棵月季花.照这样计算, 形花坛里,大约有 棵这样的月季花?
14.下图中一共有 条线段, 条射线。
15.甲、乙、丙三人每分钟分别行60米、50米、和40米,甲从B地,乙和丙从A地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙.A、B两地的距离是 米.
三、判断题
16.奇思有3件上衣和3条裤子搭配成一套衣服,一共有6种搭配方法。( )
17.从4种点心和2种饮料中各选一种搭配成早餐,共有6种不同的搭配方法。( )
18.一只口袋装有3个彩球,另一个口袋装有2个彩球,所有彩球的颜色都不相同,从两个口袋中各取一个彩球有5种不同的取法。 ( )
19.有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。( )
20.实验小学举行篮球比赛,一共有6支篮球队参加,如果每2支篮球队要赛一场,那么一共要赛10场。( )
四、计算题
21.口算。
2.5×4= 6.4÷0.8= 0.1×0.2= 0÷2.7=
7.2÷8= 1.25×10= 0.3÷0.3= 5÷0.5=
22.直接写出得数。
1.2÷0.1= 0.5×0.2= 0÷0.09= 6.8÷17=
1-0.01= 0.25÷5= 39÷1.3= 0.125×16=
五、解答题
23.如图是某社区的道路示意图。如果从学校到书店只能向东或向北走,那么从学校到书店共有几条路线?
24.小小购物员.
(1)买15个“多啦A梦”要花多少钱
(2)买24个“变形金刚”,带2500元够吗
25.奇思和妙想各有下面3张扑克牌,每人从中任意抽出一张,有哪几种可能的结果?
26.列式计算:
27.精彩的马戏每隔一段时间就开始表演.上午已经表演了四场:7:00、7:50、8:40和9:30,下面哪个时刻正好是一场表演的开始时刻
13:00 14:30 15:30 16:00
《第七单元解决问题的策略》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C D D B C B BC
1.C
【分析】每一条线段有两个端点,从7个点中选一个点作为端点有7种方法,而选第二个点有6种方法,共有7×6种方法。但是因一条线段重复一次,故实际上是7×6÷2条线段。
【详解】7×(7-1)÷2
=7×3
=21(条)
所以7个点最多可以连成21条线段。
故选:C。
【点睛】本题考查了排列组合知识的灵活应用,解答此题的关键是理解两点只能连一条线段,所以要排除重合的情况。
2.C
【分析】一个偏旁和4个汉字可以组成4个新的汉字,两个偏旁就能组合成2组4个汉字,表示2个4是多少,用乘法计算即可。
【详解】2×4=8(个)
一共可以组成8个新的汉字。
故答案为:C
【点睛】本题考查的是简单的搭配规律。用两种不同的量相乘,即可组成新的数量。
3.D
【分析】首轮(8进4)进行淘汰赛要进行4场比赛,决出4强;次轮4强的循环赛,每个班都要和另外3个班比赛,再去掉重复计算的情况,因此循环赛比赛的场数是4×3÷2=6(场),一共要比赛4+6=10(场)。
【详解】根据分析,淘汰赛要进行8÷2=4(场)
循环赛要进行:4×3÷2=6(场)
一共要比赛4+6=10(场)
【点睛】本题主要是考查搭配问题,弄清楚淘汰赛和循环赛的赛制是解题的关键。本题也可以采用枚举法进行解答。
4.C
【解析】略
5.D
【分析】要使走的路线最短,只能横向向右或纵向向下行走,以此为依据,从A到O有两种走法,然后再按照求最短路线的方法一一列举即可。
【详解】第1种:A-1-O-3-4-5-B;
第2种:A-1-O-3-9-5-B;
第3种:A-1-O-3-9-8-B;
第4种:A-1-O-6-9-8-B;
第5种:A-1-O-6-7-8-B;
第6种:A-1-O-6-9-5-B;
第7种:A-2-O-3-4-5-B;
第8种:A-2-O-3-9-5-B;
第9种:A-2-O-3-9-8-B;
第10种:A-2-O-6-9-8-B;
第11种:A-2-O-6-7-8-B;
第12种:A-2-O-6-9-5-B;
共12种;
故答案为:D。
【点睛】此题考查了排列组合问题,关键是要明确走的路线最短,只能横向向右或纵向向下行走,列举时要做到不重复、不遗漏。
6.D
【分析】由于百位上不能为0,减去百位为0的情况数,百位数有3种选择,十位数有3种选择,个位数有2种选择。运用乘法原理解答。
【详解】3×3×2
=9×2
=18(个)
故答案为:D
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。
7.B
【分析】将1元、2元、5元和10元人民币各1张任意取出2张一一列举出来即可。
【详解】每次取2张有:
1元和2元;1元和5元;1元和10元;2元和5元;2元和10元;5元和10元;共有6种;
故答案为:B。
【点睛】解答此题的关键是根据题意,能利用所给的币值,找出组成的组合,一定不要重复和遗漏。
8.C
【分析】由题意知道次央今年与爸爸的年龄相差(40-8)岁,因为两人的年龄差不会随时间变化,所以再过几年两人的年龄差也是(40-8)岁,又知道爸爸的年龄是次央年龄的3倍,由此根据差倍公式,解决问题。
【详解】(40-8)÷(3-1)
=32÷2
=16(岁)
16-8=8(年)
再过8年,爸爸的年龄是次央年龄的3倍。
故答案为:C。
【点睛】本题主要考查差倍问题,明确年龄差不变是解题的关键。
9.B
【分析】由题意得每次能框出前后两个连续的数,-共有64个数,求-共能框出几个不同的和就是求可以框出多少组合,如果以这个框的左边为开头,那么从1开始,每次都和后面的一个数组合,那么这64个数字只有64后面没有数字,其它64-1=63个都可以,由此求解。
【详解】64-1=63(个);共有得到63个不同的和。
故选B。
【点睛】此题考查了简单图形覆盖现象中的规律,本题得到相邻的两个数共有的情况数就是可以有不同的和。
10.BC
【详解】略
11. 13 7 2 8
【详解】略
12.10
【分析】13个苹果分成4堆,要求最多的一堆能放多少个;那么其余的3堆就要尽可能的少分苹果;也就是其余3堆分的数量最少时,即每堆分1个,此时第4堆的数量就是最多的,列式:13-1×3,计算即可解此题。
【详解】根据分析:
13-1×3
=13-3
=10(个)
由此可知,将13个苹果分成4堆,最多的一堆能放10个。
13.300
【详解】略
14. 6 8
【分析】要求有多少条线段,就是求端点A、B、C、D一共可以连成多少条线段。用到了搭配的知识。而求有多少条射线,一个端点引出两条射线,4个端点引出8条射线。
【详解】3+2+1=6(条)
4×2=8(条)
【点睛】在数线段、射线时,基本原则就是要按一定的顺序来数,做到不重不漏。
15.16500
【详解】试题分析:甲遇到乙后15分钟又遇到丙,则从甲遇到乙后,再和丙相遇的这15分钟里,甲丙共行了(60+40)×15=1500米,即甲乙相遇时,乙比丙多行了1500米,乙丙两人的速度差为:50﹣40=10(米/分钟),则甲乙相遇时,乙行了1500÷10=150分钟,所以A、B两地的距离为:(60+50)×150=110×150=16500(米),据此解答即可.
解答:解:(60+40)×15÷(50﹣40)×(60+50)
=100×15÷10×110
=150×110
=16500(米).
答:A、B两地相距16500米.
故答案为16500.
点评:此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出甲乙的相遇时间.
16.×
【分析】根据题意,1件上衣与每条裤子搭配一次,就有3种搭配方法,那么3件上衣与3条裤子搭配一次,就有(3×3)种不同的搭配方法。
【详解】3×3=9(种),所以3件上衣和3条裤子搭配成一套衣服,共有9种搭配方法。
故答案为:×
【点睛】此题主要考查的是搭配问题,解答此题的关键是列乘法算式得出共有多少种搭配方法。
17.×
【分析】每一种点心都可以搭配2种饮料,也就是一种点心对应2种搭配方法,4种点心对应的就是4×2=8(种)搭配方法,据此判断。
【详解】4×2=8(种),从4种点心和2种饮料中各选一种搭配成早餐,共有8种不同的搭配方法。原题说法错误。
故答案为:×
【点睛】此题考查了有关搭配问题,明确完成每一步可用的方法有几种,全部相乘即可。
18.×
【分析】分析题意,这是一个分步问题,分两步进行,先从第一个口袋中取小球,再从第二个口袋取小球,由分步计数的乘法原理计算可得答案。
【详解】各取一个小球,不论从哪个口袋中取,都不能算完成了这件事,是分步问题;
因此应分两个步骤完成,①从第一个口袋中取一个小球有3种情况,②从第二个口袋中取一个小球有2种情况,由分步乘法计数原理,共有3×2=6(种)。故原题干说法错误。
故答案为:×
【点睛】本题考查分步计数原理与分类计数原理的运用,解题时,注意分析题意,认清是分步问题还是分类问题;这是解题的关键。
19.√
【分析】由于每个小朋友都要和另外的4个小朋友握一次手,一共要握了(5×4)次,即20次;又因为两个小朋友只握一次手,去掉重复计算的情况,实际只握了(20÷2)次,即10次;据此解答。
【详解】(5-1)×5÷2
=4×5÷2
=20÷2
=10(次)
所以,有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。
故答案为:√
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况。
20.×
【分析】第一支球队要和剩下的5支球队进行比赛,要赛5场;第二支球队要和剩下的4支球队进行比赛,要赛4场;第三支球队要和剩下的3支球队进行比赛,要赛3场;第四支球队要和剩下的2支球队进行比赛,要赛2场;第五支球队要和剩下的1支球队进行比赛,要赛1场,把这些比赛场数相加,就是一共要比赛的场数,据此作答。
【详解】根据上述分析可得:
5+4+3+2+1
=9+3+2+1
=12+2+1
=14+1
=15(场)
所以实验小学举行篮球比赛,一共有6支篮球队参加,如果每2支篮球队要赛一场,那么一共要赛15场,原题说法错误。
故答案为:×
21.10;8;0.02;0
0.9;12.5;1;10
【详解】略
22.12;0.1;0;0.4;
0.99;0.05;30;2
【详解】略。
23.3条
【分析】路线一:从学校出发先向北,再一直向东,最后到达书店,如下图蓝色箭头所示;
路线二:从学校出发先向东再向北,再向东,最后到达书店,如下图红色箭头所示;
路线三:从学校出发先一直向东,再向北,最后到达书店,如下图黑色箭头所示。
【详解】由分析可知:1+1+1=3(条)
答:学校到书店一共有3条路线。
24.(1)15×32=480(元)
答:买15个“多啦A梦”要花480元
(2)24×98=2352(元)
2352<2500
答:带2500元够.
【详解】【分析】本题考点:图文应用题;整数的乘法及应用.
本题注意是根据单价、数量、总价三者之间的关系求解.
(1)用多啦A梦的单价乘上15,即可求出15个多啦A梦需要的钱数;
(2)用变形金刚的单价乘上24,即可求出24个多啦A梦需要的钱数,然后与2500元进行大小比较即可;
25.KK、JJ、QQ、KJ、KQ、JK、JQ、QK、QJ;9种
【分析】一共有3种花色,每选择一种花色都可以有3种搭配方式,3个花色就有(3×3)种搭配方式,列举出所有的可能性即可。
【详解】3×3=9(种)
K可以与K、J、Q搭配;
J可以与K、J、Q搭配;
K可以与K、J、Q搭配;
答:KK、JJ、QQ、KJ、KQ、JK、JQ、QK、QJ共9种可能的结果。
26.①400×
=
=160(米)
答:还有160米没有修.
②168×
=48+168
=216(吨)
答:土豆的重量是216吨
【详解】【分析】①首先求出没有修的占这条路的长度的几分之几;然后根据分数乘法的意义,用这条路的长度乘没有修的占的分率,求出没有修的长度是多少即可;②首先根据分数乘法的意义,用白菜的重量乘土豆比白茶多的分率,求出土豆比白菜多的重量是多少;然后用土豆比白菜多的重量加上白菜的重量,求出土豆的重量是多少即可.此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是弄清楚题中的等量关系.
27.14:30
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七单元解决问题的策略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.将7个点连成线段,任意三点不在同一条直线上,最多可以连成( )。
A.7条 B.12条 C.21条 D.28条
2.用下面2个偏旁和4个汉字,一共可以组成( )个新的汉字。
A.4 B.6 C.8 D.10
3.六年级8个班进行男子三人制篮球赛,如果首轮(8进4)进行淘汰赛,次轮进行循环赛,最后产生冠军,一共要比赛( )场。
A.7 B.8 C.9 D.10
4.小欣一家三口到影楼照全家福,摄影师有( )种排列方法。
A.3 B.1 C.6
5.如图,小蚂蚁从点A爬到点B,走最短的路线,共有( )种不同的路线。
A.6 B.8 C.10 D.12
6.用写有0、3、4、5的四张数字卡片,能摆出( )不同的三位数。
A.6个 B.12个 C.16个 D.18个
7.有1元、2元、5元和10元人民币各1张,任意取2张,可以有( )种不同的取法。
A.4 B.6 C.10 D.14
8.次央今年8岁,爸爸今年40岁,再过( )年,爸爸的年龄是次央年龄的3倍。
A.4 B.6 C.8 D.10
9.用形如的框每次框下表中的两个数,共有得到( )种不同的和。
A.62 B.63 C.64 D.65
10.看图列式计算,正确的是( )
A.9-4=5 B.5+9=14 C.9+5=14 D.9-5=4
二、填空题
11.填一填.
有 个三角形,有 个圆,有 个正方形,有 个长方形.
12.将13个苹果分成4堆,最多的一堆能放( )个。
13.估一估.
形花坛里,大约有50棵月季花.照这样计算, 形花坛里,大约有 棵这样的月季花?
14.下图中一共有 条线段, 条射线。
15.甲、乙、丙三人每分钟分别行60米、50米、和40米,甲从B地,乙和丙从A地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙.A、B两地的距离是 米.
三、判断题
16.奇思有3件上衣和3条裤子搭配成一套衣服,一共有6种搭配方法。( )
17.从4种点心和2种饮料中各选一种搭配成早餐,共有6种不同的搭配方法。( )
18.一只口袋装有3个彩球,另一个口袋装有2个彩球,所有彩球的颜色都不相同,从两个口袋中各取一个彩球有5种不同的取法。 ( )
19.有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。( )
20.实验小学举行篮球比赛,一共有6支篮球队参加,如果每2支篮球队要赛一场,那么一共要赛10场。( )
四、计算题
21.口算。
2.5×4= 6.4÷0.8= 0.1×0.2= 0÷2.7=
7.2÷8= 1.25×10= 0.3÷0.3= 5÷0.5=
22.直接写出得数。
1.2÷0.1= 0.5×0.2= 0÷0.09= 6.8÷17=
1-0.01= 0.25÷5= 39÷1.3= 0.125×16=
五、解答题
23.如图是某社区的道路示意图。如果从学校到书店只能向东或向北走,那么从学校到书店共有几条路线?
24.小小购物员.
(1)买15个“多啦A梦”要花多少钱
(2)买24个“变形金刚”,带2500元够吗
25.奇思和妙想各有下面3张扑克牌,每人从中任意抽出一张,有哪几种可能的结果?
26.列式计算:
27.精彩的马戏每隔一段时间就开始表演.上午已经表演了四场:7:00、7:50、8:40和9:30,下面哪个时刻正好是一场表演的开始时刻
13:00 14:30 15:30 16:00
《第七单元解决问题的策略》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C D D B C B BC
1.C
【分析】每一条线段有两个端点,从7个点中选一个点作为端点有7种方法,而选第二个点有6种方法,共有7×6种方法。但是因一条线段重复一次,故实际上是7×6÷2条线段。
【详解】7×(7-1)÷2
=7×3
=21(条)
所以7个点最多可以连成21条线段。
故选:C。
【点睛】本题考查了排列组合知识的灵活应用,解答此题的关键是理解两点只能连一条线段,所以要排除重合的情况。
2.C
【分析】一个偏旁和4个汉字可以组成4个新的汉字,两个偏旁就能组合成2组4个汉字,表示2个4是多少,用乘法计算即可。
【详解】2×4=8(个)
一共可以组成8个新的汉字。
故答案为:C
【点睛】本题考查的是简单的搭配规律。用两种不同的量相乘,即可组成新的数量。
3.D
【分析】首轮(8进4)进行淘汰赛要进行4场比赛,决出4强;次轮4强的循环赛,每个班都要和另外3个班比赛,再去掉重复计算的情况,因此循环赛比赛的场数是4×3÷2=6(场),一共要比赛4+6=10(场)。
【详解】根据分析,淘汰赛要进行8÷2=4(场)
循环赛要进行:4×3÷2=6(场)
一共要比赛4+6=10(场)
【点睛】本题主要是考查搭配问题,弄清楚淘汰赛和循环赛的赛制是解题的关键。本题也可以采用枚举法进行解答。
4.C
【解析】略
5.D
【分析】要使走的路线最短,只能横向向右或纵向向下行走,以此为依据,从A到O有两种走法,然后再按照求最短路线的方法一一列举即可。
【详解】第1种:A-1-O-3-4-5-B;
第2种:A-1-O-3-9-5-B;
第3种:A-1-O-3-9-8-B;
第4种:A-1-O-6-9-8-B;
第5种:A-1-O-6-7-8-B;
第6种:A-1-O-6-9-5-B;
第7种:A-2-O-3-4-5-B;
第8种:A-2-O-3-9-5-B;
第9种:A-2-O-3-9-8-B;
第10种:A-2-O-6-9-8-B;
第11种:A-2-O-6-7-8-B;
第12种:A-2-O-6-9-5-B;
共12种;
故答案为:D。
【点睛】此题考查了排列组合问题,关键是要明确走的路线最短,只能横向向右或纵向向下行走,列举时要做到不重复、不遗漏。
6.D
【分析】由于百位上不能为0,减去百位为0的情况数,百位数有3种选择,十位数有3种选择,个位数有2种选择。运用乘法原理解答。
【详解】3×3×2
=9×2
=18(个)
故答案为:D
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。
7.B
【分析】将1元、2元、5元和10元人民币各1张任意取出2张一一列举出来即可。
【详解】每次取2张有:
1元和2元;1元和5元;1元和10元;2元和5元;2元和10元;5元和10元;共有6种;
故答案为:B。
【点睛】解答此题的关键是根据题意,能利用所给的币值,找出组成的组合,一定不要重复和遗漏。
8.C
【分析】由题意知道次央今年与爸爸的年龄相差(40-8)岁,因为两人的年龄差不会随时间变化,所以再过几年两人的年龄差也是(40-8)岁,又知道爸爸的年龄是次央年龄的3倍,由此根据差倍公式,解决问题。
【详解】(40-8)÷(3-1)
=32÷2
=16(岁)
16-8=8(年)
再过8年,爸爸的年龄是次央年龄的3倍。
故答案为:C。
【点睛】本题主要考查差倍问题,明确年龄差不变是解题的关键。
9.B
【分析】由题意得每次能框出前后两个连续的数,-共有64个数,求-共能框出几个不同的和就是求可以框出多少组合,如果以这个框的左边为开头,那么从1开始,每次都和后面的一个数组合,那么这64个数字只有64后面没有数字,其它64-1=63个都可以,由此求解。
【详解】64-1=63(个);共有得到63个不同的和。
故选B。
【点睛】此题考查了简单图形覆盖现象中的规律,本题得到相邻的两个数共有的情况数就是可以有不同的和。
10.BC
【详解】略
11. 13 7 2 8
【详解】略
12.10
【分析】13个苹果分成4堆,要求最多的一堆能放多少个;那么其余的3堆就要尽可能的少分苹果;也就是其余3堆分的数量最少时,即每堆分1个,此时第4堆的数量就是最多的,列式:13-1×3,计算即可解此题。
【详解】根据分析:
13-1×3
=13-3
=10(个)
由此可知,将13个苹果分成4堆,最多的一堆能放10个。
13.300
【详解】略
14. 6 8
【分析】要求有多少条线段,就是求端点A、B、C、D一共可以连成多少条线段。用到了搭配的知识。而求有多少条射线,一个端点引出两条射线,4个端点引出8条射线。
【详解】3+2+1=6(条)
4×2=8(条)
【点睛】在数线段、射线时,基本原则就是要按一定的顺序来数,做到不重不漏。
15.16500
【详解】试题分析:甲遇到乙后15分钟又遇到丙,则从甲遇到乙后,再和丙相遇的这15分钟里,甲丙共行了(60+40)×15=1500米,即甲乙相遇时,乙比丙多行了1500米,乙丙两人的速度差为:50﹣40=10(米/分钟),则甲乙相遇时,乙行了1500÷10=150分钟,所以A、B两地的距离为:(60+50)×150=110×150=16500(米),据此解答即可.
解答:解:(60+40)×15÷(50﹣40)×(60+50)
=100×15÷10×110
=150×110
=16500(米).
答:A、B两地相距16500米.
故答案为16500.
点评:此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出甲乙的相遇时间.
16.×
【分析】根据题意,1件上衣与每条裤子搭配一次,就有3种搭配方法,那么3件上衣与3条裤子搭配一次,就有(3×3)种不同的搭配方法。
【详解】3×3=9(种),所以3件上衣和3条裤子搭配成一套衣服,共有9种搭配方法。
故答案为:×
【点睛】此题主要考查的是搭配问题,解答此题的关键是列乘法算式得出共有多少种搭配方法。
17.×
【分析】每一种点心都可以搭配2种饮料,也就是一种点心对应2种搭配方法,4种点心对应的就是4×2=8(种)搭配方法,据此判断。
【详解】4×2=8(种),从4种点心和2种饮料中各选一种搭配成早餐,共有8种不同的搭配方法。原题说法错误。
故答案为:×
【点睛】此题考查了有关搭配问题,明确完成每一步可用的方法有几种,全部相乘即可。
18.×
【分析】分析题意,这是一个分步问题,分两步进行,先从第一个口袋中取小球,再从第二个口袋取小球,由分步计数的乘法原理计算可得答案。
【详解】各取一个小球,不论从哪个口袋中取,都不能算完成了这件事,是分步问题;
因此应分两个步骤完成,①从第一个口袋中取一个小球有3种情况,②从第二个口袋中取一个小球有2种情况,由分步乘法计数原理,共有3×2=6(种)。故原题干说法错误。
故答案为:×
【点睛】本题考查分步计数原理与分类计数原理的运用,解题时,注意分析题意,认清是分步问题还是分类问题;这是解题的关键。
19.√
【分析】由于每个小朋友都要和另外的4个小朋友握一次手,一共要握了(5×4)次,即20次;又因为两个小朋友只握一次手,去掉重复计算的情况,实际只握了(20÷2)次,即10次;据此解答。
【详解】(5-1)×5÷2
=4×5÷2
=20÷2
=10(次)
所以,有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。
故答案为:√
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况。
20.×
【分析】第一支球队要和剩下的5支球队进行比赛,要赛5场;第二支球队要和剩下的4支球队进行比赛,要赛4场;第三支球队要和剩下的3支球队进行比赛,要赛3场;第四支球队要和剩下的2支球队进行比赛,要赛2场;第五支球队要和剩下的1支球队进行比赛,要赛1场,把这些比赛场数相加,就是一共要比赛的场数,据此作答。
【详解】根据上述分析可得:
5+4+3+2+1
=9+3+2+1
=12+2+1
=14+1
=15(场)
所以实验小学举行篮球比赛,一共有6支篮球队参加,如果每2支篮球队要赛一场,那么一共要赛15场,原题说法错误。
故答案为:×
21.10;8;0.02;0
0.9;12.5;1;10
【详解】略
22.12;0.1;0;0.4;
0.99;0.05;30;2
【详解】略。
23.3条
【分析】路线一:从学校出发先向北,再一直向东,最后到达书店,如下图蓝色箭头所示;
路线二:从学校出发先向东再向北,再向东,最后到达书店,如下图红色箭头所示;
路线三:从学校出发先一直向东,再向北,最后到达书店,如下图黑色箭头所示。
【详解】由分析可知:1+1+1=3(条)
答:学校到书店一共有3条路线。
24.(1)15×32=480(元)
答:买15个“多啦A梦”要花480元
(2)24×98=2352(元)
2352<2500
答:带2500元够.
【详解】【分析】本题考点:图文应用题;整数的乘法及应用.
本题注意是根据单价、数量、总价三者之间的关系求解.
(1)用多啦A梦的单价乘上15,即可求出15个多啦A梦需要的钱数;
(2)用变形金刚的单价乘上24,即可求出24个多啦A梦需要的钱数,然后与2500元进行大小比较即可;
25.KK、JJ、QQ、KJ、KQ、JK、JQ、QK、QJ;9种
【分析】一共有3种花色,每选择一种花色都可以有3种搭配方式,3个花色就有(3×3)种搭配方式,列举出所有的可能性即可。
【详解】3×3=9(种)
K可以与K、J、Q搭配;
J可以与K、J、Q搭配;
K可以与K、J、Q搭配;
答:KK、JJ、QQ、KJ、KQ、JK、JQ、QK、QJ共9种可能的结果。
26.①400×
=
=160(米)
答:还有160米没有修.
②168×
=48+168
=216(吨)
答:土豆的重量是216吨
【详解】【分析】①首先求出没有修的占这条路的长度的几分之几;然后根据分数乘法的意义,用这条路的长度乘没有修的占的分率,求出没有修的长度是多少即可;②首先根据分数乘法的意义,用白菜的重量乘土豆比白茶多的分率,求出土豆比白菜多的重量是多少;然后用土豆比白菜多的重量加上白菜的重量,求出土豆的重量是多少即可.此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是弄清楚题中的等量关系.
27.14:30
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
