河北省邢台市信都区部分学校2025届九年级下学期中考三模数学试卷(含详解)
文档属性
| 名称 | 河北省邢台市信都区部分学校2025届九年级下学期中考三模数学试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 00:00:00 | ||
图片预览



文档简介
2025年河北省邢台市信都区中考三模数学试题(6月)
一、单选题
1.下列代数式中,表示“x与1的和的相反数”的是( )
A. B. C. D.
2.如图,在直线中,可能与直线平行的是( )
A.直线 B.直线 C.直线 D.直线
3.不等式的解集如图所示,则a的值为( )
A. B.3 C. D.2
4.若,则“□”中的运算符号是( )
A. B. C. D.
5.某部门四名员工的月工资都为5000元,后来又来了一名新员工,月工资为4800元,这五名员工工资与原来四名员工工资比较,方差( )
A.变大了 B.变小了 C.没有变化 D.无法确定
6.剪纸是我国传统民间艺术之一.嘉嘉将一张圆形纸片按图3的流程进行操作,即先沿虚线对折两次,再沿虚线剪开,则展开后的剪纸形状是( )
A. B. C. D.
7.甲、乙两人进行一分钟跳绳练习,结束后,甲说:“我的跳绳个数加你的跳绳个数的刚好等于220个”;乙说:“我的跳绳个数加你的跳绳个数的刚好也等于220个”.设甲的跳绳个数为x个,乙的跳绳个数为y个,下列说法错误的是( )
A. B.
C. D.
8.如图1是多媒体上展示的一道数学题,淇淇的部分作图过程如图2所示,接下来淇淇以点C为圆心,长为半径作弧交射线于点D,连接,则四边形即为所求.对于淇淇得到的四边形,下列说法正确的是( )
A.四边形一定是平行四边形
B.当时,四边形一定是矩形
C.四边形一定不是平行四边形
D.当时,四边形是平行四边形
9.如图,点A,C在不完整的数轴上,对应的数分别为a,c,原点与点A,C均不重合.若,则方程的根的情况是( )
A.没有实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.两根之和为
10.下列图形分别为正方形、圆、扇形、等边三角形(相关数据如图所示),长度为1的线段可以在图形的内部及边界通过移转(即平移或旋转),自由地从竖放移转到横放,且图形面积最小的是( )
A. B. C. D.
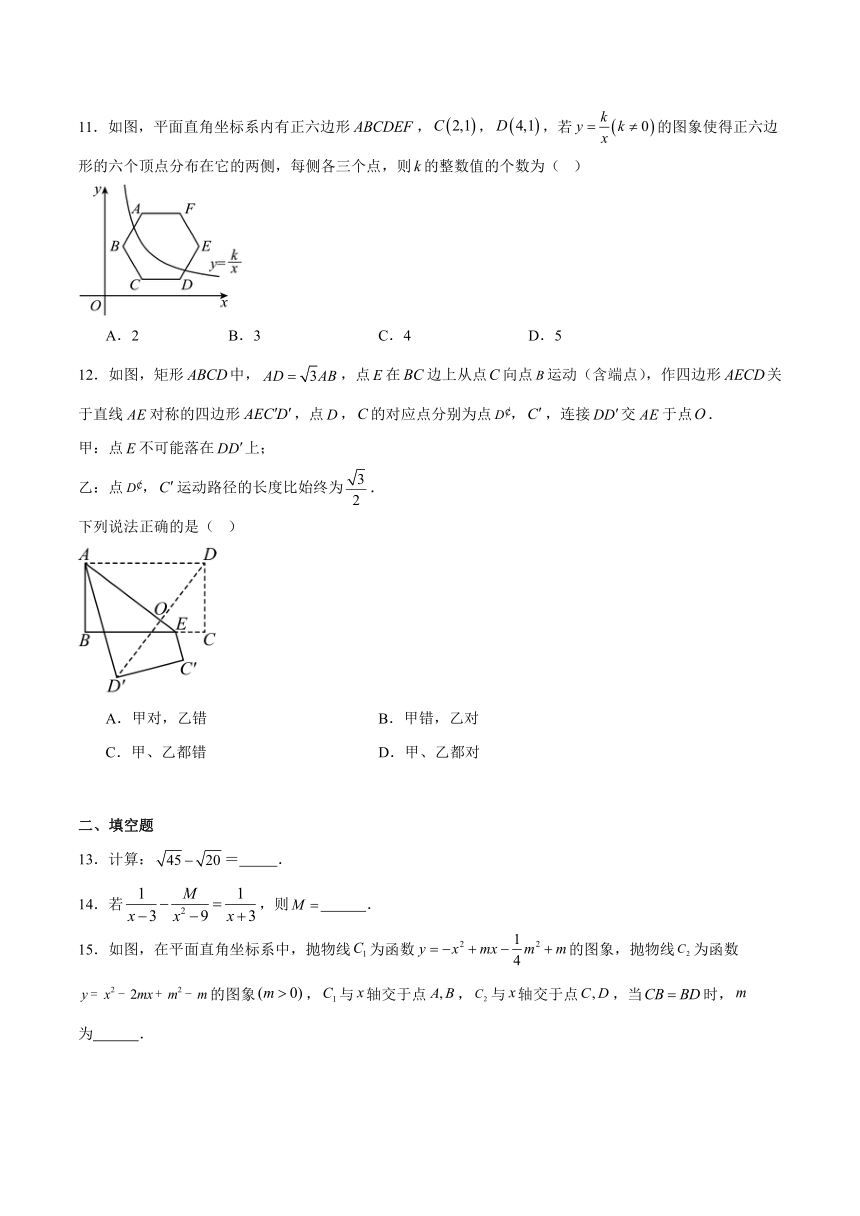
11.如图,平面直角坐标系内有正六边形,,,若的图象使得正六边形的六个顶点分布在它的两侧,每侧各三个点,则的整数值的个数为( )
A.2 B.3 C.4 D.5
12.如图,矩形中,,点在边上从点向点运动(含端点),作四边形关于直线对称的四边形,点,的对应点分别为点,,连接交于点.
甲:点不可能落在上;
乙:点,运动路径的长度比始终为.
下列说法正确的是( )
A.甲对,乙错 B.甲错,乙对
C.甲、乙都错 D.甲、乙都对
二、填空题
13.计算:= .
14.若,则 .
15.如图,在平面直角坐标系中,抛物线为函数的图象,抛物线为函数的图象,与轴交于点,与轴交于点,当时,为 .
16.如图,某正多边形花坛的边沿被树冠挡住了大部分,为其中一边,点为两条邻边延长线的交点,测得,.
(1)该正多边形的边数为 ;
(2)该正多边形的面积为 .
三、解答题
17.如图,利用计算机小程序做数学游戏:
第一步,点击“数字小助手”随机生成一个整数;
第二步,点击“运算百宝箱”依次弹出两张不同的运算卡片;
第三步,对第一步中生成的整数,按照第二步中弹出的卡片内容依次进行计算.
例如:第一步,点击“数字小助手”生成整数3;
第二步,点击“运算百宝箱”依次弹出卡片和;
第三步,计算.
(1)若第一步中生成的整数为5,第二步中弹出的卡片依次为和,请完成第三步的计算;
(2)若第一步中生成的整数为,第二步中弹出的卡片依次为和,第三步的计算结果是一个正数,求的最小整数值.
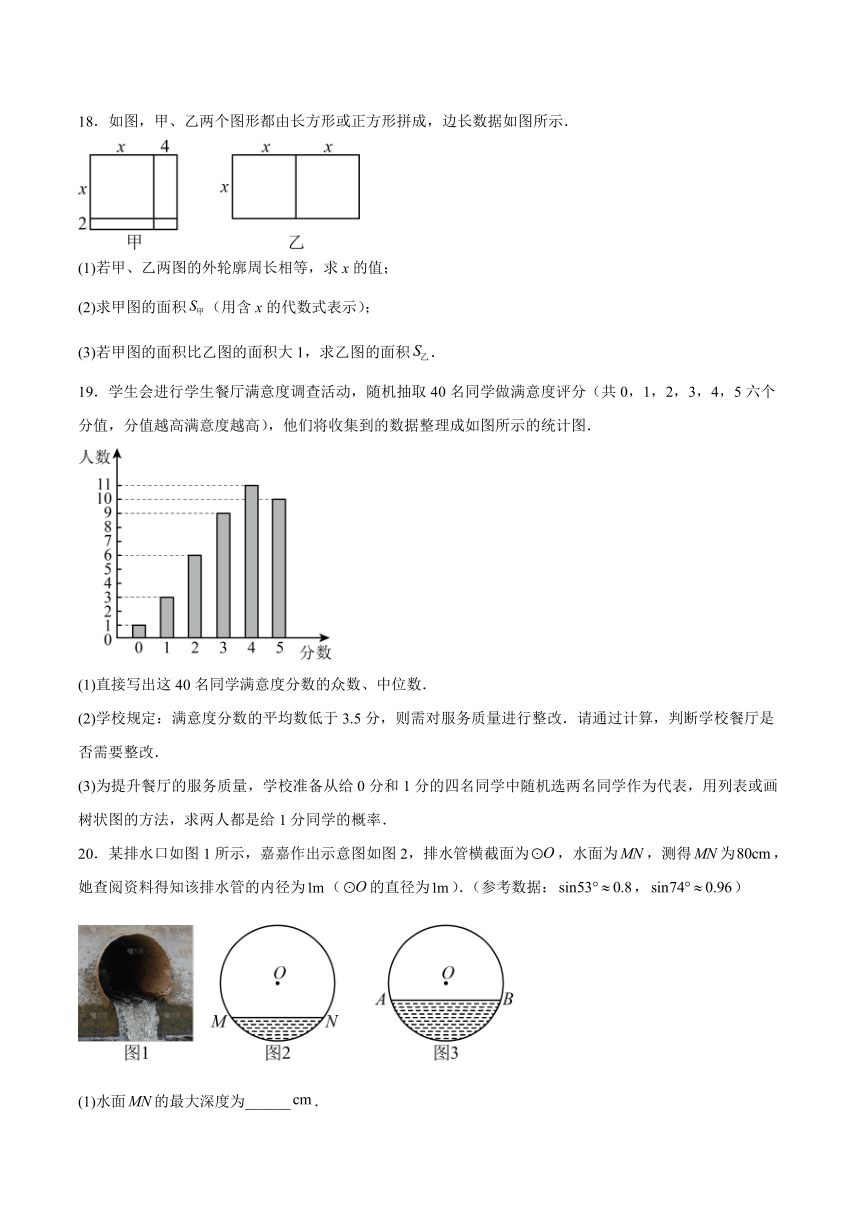
18.如图,甲、乙两个图形都由长方形或正方形拼成,边长数据如图所示.
(1)若甲、乙两图的外轮廓周长相等,求x的值;
(2)求甲图的面积(用含x的代数式表示);
(3)若甲图的面积比乙图的面积大1,求乙图的面积.
19.学生会进行学生餐厅满意度调查活动,随机抽取40名同学做满意度评分(共0,1,2,3,4,5六个分值,分值越高满意度越高),他们将收集到的数据整理成如图所示的统计图.
(1)直接写出这40名同学满意度分数的众数、中位数.
(2)学校规定:满意度分数的平均数低于3.5分,则需对服务质量进行整改.请通过计算,判断学校餐厅是否需要整改.
(3)为提升餐厅的服务质量,学校准备从给0分和1分的四名同学中随机选两名同学作为代表,用列表或画树状图的方法,求两人都是给1分同学的概率.
20.某排水口如图1所示,嘉嘉作出示意图如图2,排水管横截面为,水面为,测得为,她查阅资料得知该排水管的内径为(的直径为).(参考数据:,)
(1)水面的最大深度为______.
(2)几天后水位上涨,排水管横截面如图3,水面宽度为.
①求水位上涨的高度.
②按规定,排水口水流横截面积(阴影部分)大于排水管横截面积的时需要清淤.请通过计算,判断现在是否需要清淤.
21.嘉嘉在几何画板软件上做数学实验:如图,在平面直角坐标系中,取,构造直线.
(1)求直线的解析式.
(2)嘉嘉将直线在轴下方的部分沿轴翻折,得到射线,取,线段以每秒个单位长度的速度沿射线方向匀速运动,运动时间为秒.
①点运动到点的初始位置时,用时______秒.
②求点运动到线段上时的坐标;
③直接写出仅有一个点在内部(含角的两边)时的取值范围.
22.淇淇家想在某小区购买一套在建住宅,但拟购单元楼正南方有一栋已建好的高楼可能影响采光,淇淇想用所学知识帮家里选合适的楼层.她收集数据并画出示意图如图1,为南面单元楼的北面墙,为未建好的拟购单元楼的南面墙,楼北面为开阔地带,过点的太阳光线落在楼的点处,楼为33层,楼规划18层,每层均为,楼间距为,该小区所在纬度为.(楼层和楼板的厚度忽略不计;参考数据:,)
[知识链接:冬至日正午太阳高度角(当地纬度),即正午太阳光线与地面的夹角]
(1)淇淇家如果想在冬至日正午有太阳直射光,则淇淇家可以买第几层楼?
(2)综合考虑后淇淇家买在了10层,某天正午刚好有太阳光线照在她家落地窗的下沿处,如图2,请推算此时的太阳高度角和本单元楼照在地面上的影子的长.
23.“投壶”是古人宴会时的一种娱乐游戏,参与者需站在一定距离外,将箭矢投入壶中,以投入的数量和方式计算得分.嘉嘉体验了投壶游戏后作出示意图如图1,以投壶者所站位置为原点,地面为轴,为个单位长度建立平面直角坐标系,投掷过程中箭矢前端点的运动路径可看作抛物线的一部分,点从点处出手,矩形为壶,,,.
(1)如图1,,若点为抛物线的顶点,,且抛物线经过点.
①求抛物线的解析式;
②若点最终落在上,求此时的长;
③竖直提高点的出手位置(点),使点落在上(不含边界),求的取值范围.
(2)如图2,调整出手的力度和角度,使抛物线在点处到达最高点.若点经过点正上方处,直接写出点在点正上方的距离(用含的式子表示).
24.如图1,中,,,为边上一点(不与端点重合),沿折叠使点落在点处,交于点,连接.
(1)如图1,当时,
①求证:;
②求的长度.
(2)如图2,当时,求的长度.
(3)如图3,当为中点时,直接写出的长度.
(4)在(1)的条件下,将的点在边上滑动到点,点随之在边上滑动到点,点的对应点为点,如图4,直接写出点与点的最大距离.
参考答案
1.B
解:∵x与1的和是,
∴x与1的和的相反数为,
故选B.
2.D
解:直线都与直线相交,直线可能与直线平行,
故选:D.
3.B
解:由题意,得解集为.
∵,
则,
,
,
故选B.
4.C
解:,
∴与的积为,
故选C.
5.A
原工资都为5000元,方差为0,第五名员工工资为4800元,波动变大,方差变大了,
故选A.
6.A
解:A、中右下角的图符合图3最右边的图,符合题意;
B、中右下角的图不符合图3最右边的图,不符合题意;
C、中右下角的图不符合图3最右边的图,不符合题意;
D、中右下角的图不符合图3最右边的图,不符合题意;
故选:A.
7.D
解:由题意,可列方程组为.
得,
化简得,
解得,
故选:D.
8.B
解:平分.
,
,
,
,
.以点为圆心,长为半径作弧交射线于点,点会有两个位置,右侧的点可以使四边形为平行四边形,左侧的点使四边形为梯形,
四边形可能是平行四边形.
当时,点仅会有一个位置,故四边形一定是矩形,
故选B.
9.B
解:根据题意可知,,
,,
为负数,为正数,
,异号,
,
,
方程有两个不相等的实数根,两根之和为,
故选:B.
10.D
解:A、边长为1,所以长度为1的线段可在图形内自由地从竖放移转到横放,其面积为1;
B、其直径为1,所以长度为1的线段可在图形内自由地从竖放移转到横放,其面积为;
C、长度为1的线段不可以在图形内竖放;
D、长度为1的线段可先旋转到边上,再通过平移和旋转即可在图形内从竖放移转到横放,其边长为,所以面积为;
故选:D.
11.C
解:,
,
多边形是正六边形,
,其内角和为,
,
连接,作于,如图所示:
,,,
,,
,
,
,
,
.
当过点时,;
当过点时,;
,
则可取5,6,7,8,共4个整数值,
故选:C.
12.D
解:如图,连接,,
四边形关于直线对称的四边形,
,,,
,
点在以为直径的半圆上,该半圆与没有交点,而点在上,
点与点不会重合,即点不可能落在上,故甲对;
四边形是矩形,
,,
,
,
,
,
从点在点位置开始,点,运动路径的长度为以点为圆心,分别以,为半径的弧长,且与转过的角度相等,
,
点,运动路径的长度比始终为,故乙对;
故选:D.
13.
=
=
故答案是:.
14.6
解:,
,
,
,
.
故答案为:6.
15.4
解:,
∴的中点为,
∵时,为的中点,
∴,
∵在的图象上,
,
解得或(舍).
故答案为:4.
16. 8 /
解:(1),
正多边形的外角,
边数.
(2)如图,
∴,
∴,
,
,
该正多边形的面积
.
17.(1)见解析
(2)
(1)解:.
(2)解:由题意,得,
,
的最小整数值为.
18.(1)
(2)
(3)
(1)解:由题意,得,
解得;
(2)解:;
(3)解:由题意,得,
∴,
∴,
∴,
解得或,
∵,
∴,
∴.
19.(1)众数为4分,中位数为4分
(2)需要整改
(3)
(1)解:0分的人数有1人,1分的人数有3人,2分的人数有6人,3分的人数有9人,4分的人数有11人,5分的人数有10人,
∴满意度分数的众数为4分,中位数为第20,21位的平均数,即分.
(2)解:满意度的平均数
.
,
学校餐厅需要整改.
(3)解:设给0分的同学为,给1分的同学为.列表如下:
-
-
-
-
共12种等可能的结果,两人都是给1分的同学有6种结果,
两人都是给1分的同学).
20.(1)20
(2)①;②不用清淤
(1)解:如图1,过点作于点,交于点,连接.
由题意得,
,
,
水面的最大深度为.
故答案为:20;
(2)①如图2,过点作于点,连接,.
由题意得,
,
水位上涨的高度为.
② ,且,
,
,
,
,
,
不用清淤.
21.(1)
(2)①2;②;③或
(1)解:设直线的解析式为.
,
,
解得,
直线的解析式为.
(2)解:①,
,
(秒).
故答案为:2;
②,
∴设直线的解析式为,
∴,
解得,,
直线的解析式为,
联立直线和直线的解析式,得,
解得,
点运动到线段上时的坐标为.
③或.
由②得,点运动到线段上时的坐标为,
∴秒后点运动到上,
由①得点运动到点的初始位置时,用时2秒,
∴,即秒后点运动到上,
∵直线在轴下方的部分沿轴翻折,得到射线,,
∴当时,,
∴点在直线上,则点在上,
又点在上,
∴设直线的解析式为,
∴,
解得,,
得直线,
故联立直线和直线的解析式,得,
解得,
直线与的交点为,
,
到秒,都在内部,秒后点运动到上,再过2秒,即秒后点运动到上,
或.
22.(1)18层
(2)
(1)解:如图1,过点作于点,则,
冬至日正午太阳高度角,
,
,
,
,
,
,即17层及以下没有直射光,
淇淇家可以买第18层楼.
(2)解:如图2,过点作于点,
由题意得,则,
,
,即此时的太阳高度角的正切值为,
,
此时太阳高度角为,
,即,
,
即本单元楼照在地面上的影子的长为.
23.(1)①;②;③
(2)
(1)解:①由题意,得抛物线的解析式为,
又抛物线过点,
,
,
抛物线的解析式为.
②抛物线的解析式为,
当时,,即,
.
③由②可得抛物线经过点,
要经过点,
,
抛物线经过点时,,
,
当时,点落在上.
(2)解:.
顶点,
抛物线解析式为,
抛物线过点,
,
,
抛物线解析式为,且抛物线过,
,
,
当时,
,
,
点在点正上方处.
24.(1)①见解析;②
(2)
(3)
(4)
(1)解:①证明:,
,
,
,
,
又,
,
.
②,
∴,
当时,,
,
又,
.
(2)解:如图1,过点作于点,
,
设,则,
,
,
,
,
.
(3)解:如图2,连接,延长交于点,
由折叠可得为中点,
,
设,
,,
,
,
解得,
.
(4)解:.
由(1)可得,当时,,则,
如图所示,作的外接圆,过点作于点,过点作延长线于点,连接,
∵,
∴四边形是矩形,则,
由(1)②得,
,
∵,则,
,
∴,,
,
,
当点在同一直线上时,点与点的距离最大,最大值为,
最大距离为.
一、单选题
1.下列代数式中,表示“x与1的和的相反数”的是( )
A. B. C. D.
2.如图,在直线中,可能与直线平行的是( )
A.直线 B.直线 C.直线 D.直线
3.不等式的解集如图所示,则a的值为( )
A. B.3 C. D.2
4.若,则“□”中的运算符号是( )
A. B. C. D.
5.某部门四名员工的月工资都为5000元,后来又来了一名新员工,月工资为4800元,这五名员工工资与原来四名员工工资比较,方差( )
A.变大了 B.变小了 C.没有变化 D.无法确定
6.剪纸是我国传统民间艺术之一.嘉嘉将一张圆形纸片按图3的流程进行操作,即先沿虚线对折两次,再沿虚线剪开,则展开后的剪纸形状是( )
A. B. C. D.
7.甲、乙两人进行一分钟跳绳练习,结束后,甲说:“我的跳绳个数加你的跳绳个数的刚好等于220个”;乙说:“我的跳绳个数加你的跳绳个数的刚好也等于220个”.设甲的跳绳个数为x个,乙的跳绳个数为y个,下列说法错误的是( )
A. B.
C. D.
8.如图1是多媒体上展示的一道数学题,淇淇的部分作图过程如图2所示,接下来淇淇以点C为圆心,长为半径作弧交射线于点D,连接,则四边形即为所求.对于淇淇得到的四边形,下列说法正确的是( )
A.四边形一定是平行四边形
B.当时,四边形一定是矩形
C.四边形一定不是平行四边形
D.当时,四边形是平行四边形
9.如图,点A,C在不完整的数轴上,对应的数分别为a,c,原点与点A,C均不重合.若,则方程的根的情况是( )
A.没有实数根 B.有两个不相等的实数根
C.有两个相等的实数根 D.两根之和为
10.下列图形分别为正方形、圆、扇形、等边三角形(相关数据如图所示),长度为1的线段可以在图形的内部及边界通过移转(即平移或旋转),自由地从竖放移转到横放,且图形面积最小的是( )
A. B. C. D.
11.如图,平面直角坐标系内有正六边形,,,若的图象使得正六边形的六个顶点分布在它的两侧,每侧各三个点,则的整数值的个数为( )
A.2 B.3 C.4 D.5
12.如图,矩形中,,点在边上从点向点运动(含端点),作四边形关于直线对称的四边形,点,的对应点分别为点,,连接交于点.
甲:点不可能落在上;
乙:点,运动路径的长度比始终为.
下列说法正确的是( )
A.甲对,乙错 B.甲错,乙对
C.甲、乙都错 D.甲、乙都对
二、填空题
13.计算:= .
14.若,则 .
15.如图,在平面直角坐标系中,抛物线为函数的图象,抛物线为函数的图象,与轴交于点,与轴交于点,当时,为 .
16.如图,某正多边形花坛的边沿被树冠挡住了大部分,为其中一边,点为两条邻边延长线的交点,测得,.
(1)该正多边形的边数为 ;
(2)该正多边形的面积为 .
三、解答题
17.如图,利用计算机小程序做数学游戏:
第一步,点击“数字小助手”随机生成一个整数;
第二步,点击“运算百宝箱”依次弹出两张不同的运算卡片;
第三步,对第一步中生成的整数,按照第二步中弹出的卡片内容依次进行计算.
例如:第一步,点击“数字小助手”生成整数3;
第二步,点击“运算百宝箱”依次弹出卡片和;
第三步,计算.
(1)若第一步中生成的整数为5,第二步中弹出的卡片依次为和,请完成第三步的计算;
(2)若第一步中生成的整数为,第二步中弹出的卡片依次为和,第三步的计算结果是一个正数,求的最小整数值.
18.如图,甲、乙两个图形都由长方形或正方形拼成,边长数据如图所示.
(1)若甲、乙两图的外轮廓周长相等,求x的值;
(2)求甲图的面积(用含x的代数式表示);
(3)若甲图的面积比乙图的面积大1,求乙图的面积.
19.学生会进行学生餐厅满意度调查活动,随机抽取40名同学做满意度评分(共0,1,2,3,4,5六个分值,分值越高满意度越高),他们将收集到的数据整理成如图所示的统计图.
(1)直接写出这40名同学满意度分数的众数、中位数.
(2)学校规定:满意度分数的平均数低于3.5分,则需对服务质量进行整改.请通过计算,判断学校餐厅是否需要整改.
(3)为提升餐厅的服务质量,学校准备从给0分和1分的四名同学中随机选两名同学作为代表,用列表或画树状图的方法,求两人都是给1分同学的概率.
20.某排水口如图1所示,嘉嘉作出示意图如图2,排水管横截面为,水面为,测得为,她查阅资料得知该排水管的内径为(的直径为).(参考数据:,)
(1)水面的最大深度为______.
(2)几天后水位上涨,排水管横截面如图3,水面宽度为.
①求水位上涨的高度.
②按规定,排水口水流横截面积(阴影部分)大于排水管横截面积的时需要清淤.请通过计算,判断现在是否需要清淤.
21.嘉嘉在几何画板软件上做数学实验:如图,在平面直角坐标系中,取,构造直线.
(1)求直线的解析式.
(2)嘉嘉将直线在轴下方的部分沿轴翻折,得到射线,取,线段以每秒个单位长度的速度沿射线方向匀速运动,运动时间为秒.
①点运动到点的初始位置时,用时______秒.
②求点运动到线段上时的坐标;
③直接写出仅有一个点在内部(含角的两边)时的取值范围.
22.淇淇家想在某小区购买一套在建住宅,但拟购单元楼正南方有一栋已建好的高楼可能影响采光,淇淇想用所学知识帮家里选合适的楼层.她收集数据并画出示意图如图1,为南面单元楼的北面墙,为未建好的拟购单元楼的南面墙,楼北面为开阔地带,过点的太阳光线落在楼的点处,楼为33层,楼规划18层,每层均为,楼间距为,该小区所在纬度为.(楼层和楼板的厚度忽略不计;参考数据:,)
[知识链接:冬至日正午太阳高度角(当地纬度),即正午太阳光线与地面的夹角]
(1)淇淇家如果想在冬至日正午有太阳直射光,则淇淇家可以买第几层楼?
(2)综合考虑后淇淇家买在了10层,某天正午刚好有太阳光线照在她家落地窗的下沿处,如图2,请推算此时的太阳高度角和本单元楼照在地面上的影子的长.
23.“投壶”是古人宴会时的一种娱乐游戏,参与者需站在一定距离外,将箭矢投入壶中,以投入的数量和方式计算得分.嘉嘉体验了投壶游戏后作出示意图如图1,以投壶者所站位置为原点,地面为轴,为个单位长度建立平面直角坐标系,投掷过程中箭矢前端点的运动路径可看作抛物线的一部分,点从点处出手,矩形为壶,,,.
(1)如图1,,若点为抛物线的顶点,,且抛物线经过点.
①求抛物线的解析式;
②若点最终落在上,求此时的长;
③竖直提高点的出手位置(点),使点落在上(不含边界),求的取值范围.
(2)如图2,调整出手的力度和角度,使抛物线在点处到达最高点.若点经过点正上方处,直接写出点在点正上方的距离(用含的式子表示).
24.如图1,中,,,为边上一点(不与端点重合),沿折叠使点落在点处,交于点,连接.
(1)如图1,当时,
①求证:;
②求的长度.
(2)如图2,当时,求的长度.
(3)如图3,当为中点时,直接写出的长度.
(4)在(1)的条件下,将的点在边上滑动到点,点随之在边上滑动到点,点的对应点为点,如图4,直接写出点与点的最大距离.
参考答案
1.B
解:∵x与1的和是,
∴x与1的和的相反数为,
故选B.
2.D
解:直线都与直线相交,直线可能与直线平行,
故选:D.
3.B
解:由题意,得解集为.
∵,
则,
,
,
故选B.
4.C
解:,
∴与的积为,
故选C.
5.A
原工资都为5000元,方差为0,第五名员工工资为4800元,波动变大,方差变大了,
故选A.
6.A
解:A、中右下角的图符合图3最右边的图,符合题意;
B、中右下角的图不符合图3最右边的图,不符合题意;
C、中右下角的图不符合图3最右边的图,不符合题意;
D、中右下角的图不符合图3最右边的图,不符合题意;
故选:A.
7.D
解:由题意,可列方程组为.
得,
化简得,
解得,
故选:D.
8.B
解:平分.
,
,
,
,
.以点为圆心,长为半径作弧交射线于点,点会有两个位置,右侧的点可以使四边形为平行四边形,左侧的点使四边形为梯形,
四边形可能是平行四边形.
当时,点仅会有一个位置,故四边形一定是矩形,
故选B.
9.B
解:根据题意可知,,
,,
为负数,为正数,
,异号,
,
,
方程有两个不相等的实数根,两根之和为,
故选:B.
10.D
解:A、边长为1,所以长度为1的线段可在图形内自由地从竖放移转到横放,其面积为1;
B、其直径为1,所以长度为1的线段可在图形内自由地从竖放移转到横放,其面积为;
C、长度为1的线段不可以在图形内竖放;
D、长度为1的线段可先旋转到边上,再通过平移和旋转即可在图形内从竖放移转到横放,其边长为,所以面积为;
故选:D.
11.C
解:,
,
多边形是正六边形,
,其内角和为,
,
连接,作于,如图所示:
,,,
,,
,
,
,
,
.
当过点时,;
当过点时,;
,
则可取5,6,7,8,共4个整数值,
故选:C.
12.D
解:如图,连接,,
四边形关于直线对称的四边形,
,,,
,
点在以为直径的半圆上,该半圆与没有交点,而点在上,
点与点不会重合,即点不可能落在上,故甲对;
四边形是矩形,
,,
,
,
,
,
从点在点位置开始,点,运动路径的长度为以点为圆心,分别以,为半径的弧长,且与转过的角度相等,
,
点,运动路径的长度比始终为,故乙对;
故选:D.
13.
=
=
故答案是:.
14.6
解:,
,
,
,
.
故答案为:6.
15.4
解:,
∴的中点为,
∵时,为的中点,
∴,
∵在的图象上,
,
解得或(舍).
故答案为:4.
16. 8 /
解:(1),
正多边形的外角,
边数.
(2)如图,
∴,
∴,
,
,
该正多边形的面积
.
17.(1)见解析
(2)
(1)解:.
(2)解:由题意,得,
,
的最小整数值为.
18.(1)
(2)
(3)
(1)解:由题意,得,
解得;
(2)解:;
(3)解:由题意,得,
∴,
∴,
∴,
解得或,
∵,
∴,
∴.
19.(1)众数为4分,中位数为4分
(2)需要整改
(3)
(1)解:0分的人数有1人,1分的人数有3人,2分的人数有6人,3分的人数有9人,4分的人数有11人,5分的人数有10人,
∴满意度分数的众数为4分,中位数为第20,21位的平均数,即分.
(2)解:满意度的平均数
.
,
学校餐厅需要整改.
(3)解:设给0分的同学为,给1分的同学为.列表如下:
-
-
-
-
共12种等可能的结果,两人都是给1分的同学有6种结果,
两人都是给1分的同学).
20.(1)20
(2)①;②不用清淤
(1)解:如图1,过点作于点,交于点,连接.
由题意得,
,
,
水面的最大深度为.
故答案为:20;
(2)①如图2,过点作于点,连接,.
由题意得,
,
水位上涨的高度为.
② ,且,
,
,
,
,
,
不用清淤.
21.(1)
(2)①2;②;③或
(1)解:设直线的解析式为.
,
,
解得,
直线的解析式为.
(2)解:①,
,
(秒).
故答案为:2;
②,
∴设直线的解析式为,
∴,
解得,,
直线的解析式为,
联立直线和直线的解析式,得,
解得,
点运动到线段上时的坐标为.
③或.
由②得,点运动到线段上时的坐标为,
∴秒后点运动到上,
由①得点运动到点的初始位置时,用时2秒,
∴,即秒后点运动到上,
∵直线在轴下方的部分沿轴翻折,得到射线,,
∴当时,,
∴点在直线上,则点在上,
又点在上,
∴设直线的解析式为,
∴,
解得,,
得直线,
故联立直线和直线的解析式,得,
解得,
直线与的交点为,
,
到秒,都在内部,秒后点运动到上,再过2秒,即秒后点运动到上,
或.
22.(1)18层
(2)
(1)解:如图1,过点作于点,则,
冬至日正午太阳高度角,
,
,
,
,
,
,即17层及以下没有直射光,
淇淇家可以买第18层楼.
(2)解:如图2,过点作于点,
由题意得,则,
,
,即此时的太阳高度角的正切值为,
,
此时太阳高度角为,
,即,
,
即本单元楼照在地面上的影子的长为.
23.(1)①;②;③
(2)
(1)解:①由题意,得抛物线的解析式为,
又抛物线过点,
,
,
抛物线的解析式为.
②抛物线的解析式为,
当时,,即,
.
③由②可得抛物线经过点,
要经过点,
,
抛物线经过点时,,
,
当时,点落在上.
(2)解:.
顶点,
抛物线解析式为,
抛物线过点,
,
,
抛物线解析式为,且抛物线过,
,
,
当时,
,
,
点在点正上方处.
24.(1)①见解析;②
(2)
(3)
(4)
(1)解:①证明:,
,
,
,
,
又,
,
.
②,
∴,
当时,,
,
又,
.
(2)解:如图1,过点作于点,
,
设,则,
,
,
,
,
.
(3)解:如图2,连接,延长交于点,
由折叠可得为中点,
,
设,
,,
,
,
解得,
.
(4)解:.
由(1)可得,当时,,则,
如图所示,作的外接圆,过点作于点,过点作延长线于点,连接,
∵,
∴四边形是矩形,则,
由(1)②得,
,
∵,则,
,
∴,,
,
,
当点在同一直线上时,点与点的距离最大,最大值为,
最大距离为.
同课章节目录
