浙江省嘉兴市2024~2025学年第二学期高二期末检测数学试卷(图片版,含答案)
文档属性
| 名称 | 浙江省嘉兴市2024~2025学年第二学期高二期末检测数学试卷(图片版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 20:42:58 | ||
图片预览




文档简介
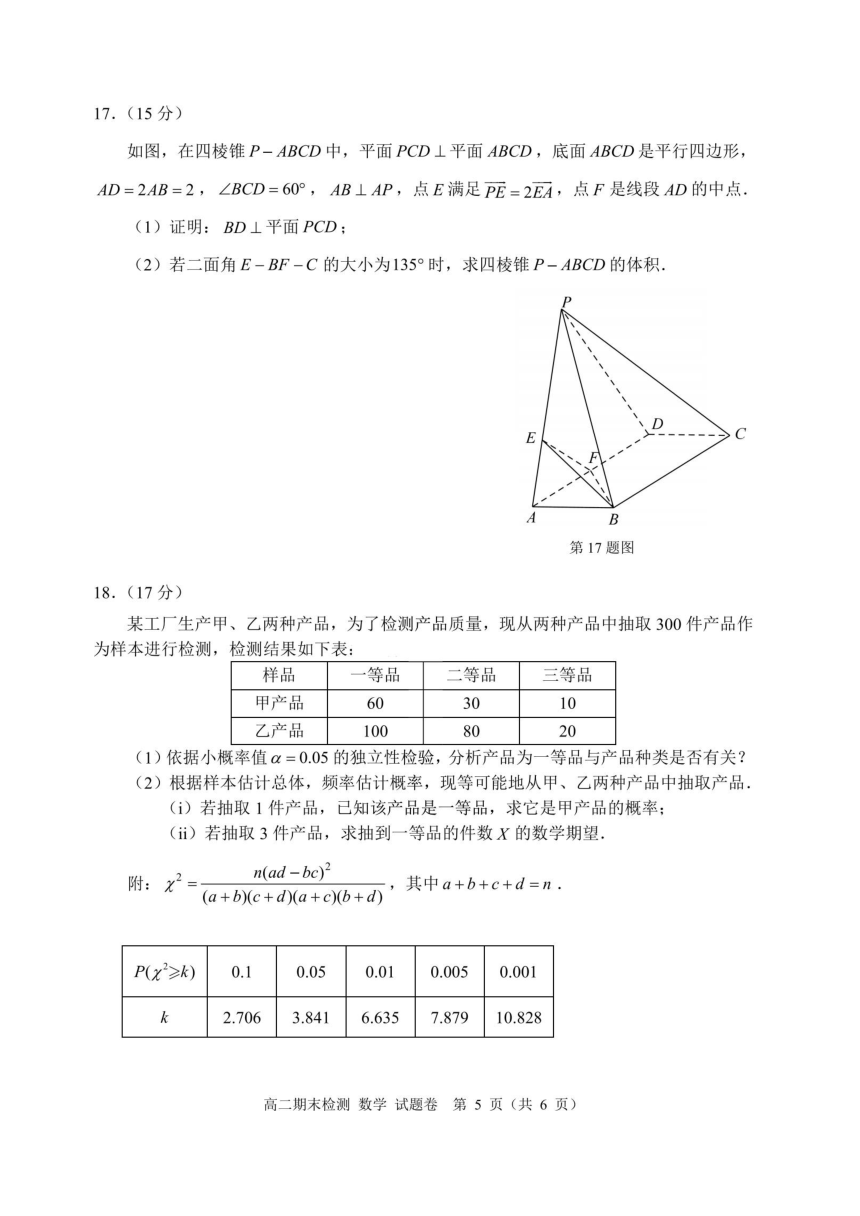
19.(17分)
设S,T是两个非空数集,函数f(x)的定义域为R,若对任意x,x2∈R,当x-x2∈S
时,f(x)-f(x2)∈T,则称f(x)为(S,T)函数.
(1)设S=[1,+oo),T=[2,+o),f(x)=cx+c是(S,T)函数,求实数k的取值范围;
(2)设S={,T={2},f(x)是(S,T)函数,当x∈[0,1)时,f(x)=4sim(元),求
y=f(x)-2x在[0,+oo)上的值域;
(3)设S=T=[2,2门(a∈R),f)是(S,)函数,证明:f)是({n2},{n2
(n∈N*)函数.
高二期末检测数学式颗卷第6页(共6页)
嘉兴市2024~2025学年第二学期期末检测
高二数学参考答案
(2025.6)
单选题(40分)
1~8 DABD
BCDC;
二、多选题(18分)
9.ABD;
10.BD;
11.ACD;
三
、】
填空题(15分)
12.1;
13.24;
14.4-2W2;
8.答案:C.
解法1:因为sinx=sin(x-),所以x+x-t=元+2kπ,keZ,故x=+花+k,
22
因为A,B,C为连续三个交点,故不妨设k=0,1,2,
一十
t5弧》
221
22
所以4C=2π,点B到AC的距离h=2cos2
所以6写-与解9行=号+,所以t=±号
2-
23
±2r+2k元,k∈Z,
所以1=2亚符合题意,故选C
3
解法2:如图,分析图象可知,AC=2π,且ACk轴,y4=-a,故4=±2
高二期末检测数学参考答案第1页(共10页)
0当=2时,如图,y=snx-)图象由y=sinx图象向右平移了元-元=2个单位,
1
663
故t
2元+2k元,k∈Z:
3
②当y4=-
时,须图,yn图用Vy=nX图酸向移了后4个印
2
63
4π
位,故t=
+2kπ,k∈Z.
3
综上,1-2+2km或:=
4π
+2kπ,k∈Z.故选C.
3
11.答案:ACD
解析:由图像可知AC正确,
对于D选项,当k>0时,g(x)=r+b与f(x)=e“相切,设切点为(x,eo),则f'(x)=e,
k=eto
则
,则b=k-klnk,令h(k)=2k-klnk,则h'(k)=1-lnk,所以y=()在
eo=kxo+b
(0,e)上单调递增,在(e,+o)上单调递减,所以h(k)max=h(e)=e,即k+b的最大值为e.
另解:g(I)=k+b,即g(x)=c+b与f(x)=e“相切时,己知求g(I)的最大值,由图象可
知,g(x)=x+b与f(x)=e相切于点(l,e)时,k+b最大,即k+b的最大值为e.
高一期末检测数学参老答案第2页(共10页)
设S,T是两个非空数集,函数f(x)的定义域为R,若对任意x,x2∈R,当x-x2∈S
时,f(x)-f(x2)∈T,则称f(x)为(S,T)函数.
(1)设S=[1,+oo),T=[2,+o),f(x)=cx+c是(S,T)函数,求实数k的取值范围;
(2)设S={,T={2},f(x)是(S,T)函数,当x∈[0,1)时,f(x)=4sim(元),求
y=f(x)-2x在[0,+oo)上的值域;
(3)设S=T=[2,2门(a∈R),f)是(S,)函数,证明:f)是({n2},{n2
(n∈N*)函数.
高二期末检测数学式颗卷第6页(共6页)
嘉兴市2024~2025学年第二学期期末检测
高二数学参考答案
(2025.6)
单选题(40分)
1~8 DABD
BCDC;
二、多选题(18分)
9.ABD;
10.BD;
11.ACD;
三
、】
填空题(15分)
12.1;
13.24;
14.4-2W2;
8.答案:C.
解法1:因为sinx=sin(x-),所以x+x-t=元+2kπ,keZ,故x=+花+k,
22
因为A,B,C为连续三个交点,故不妨设k=0,1,2,
一十
t5弧》
221
22
所以4C=2π,点B到AC的距离h=2cos2
所以6写-与解9行=号+,所以t=±号
2-
23
±2r+2k元,k∈Z,
所以1=2亚符合题意,故选C
3
解法2:如图,分析图象可知,AC=2π,且ACk轴,y4=-a,故4=±2
高二期末检测数学参考答案第1页(共10页)
0当=2时,如图,y=snx-)图象由y=sinx图象向右平移了元-元=2个单位,
1
663
故t
2元+2k元,k∈Z:
3
②当y4=-
时,须图,yn图用Vy=nX图酸向移了后4个印
2
63
4π
位,故t=
+2kπ,k∈Z.
3
综上,1-2+2km或:=
4π
+2kπ,k∈Z.故选C.
3
11.答案:ACD
解析:由图像可知AC正确,
对于D选项,当k>0时,g(x)=r+b与f(x)=e“相切,设切点为(x,eo),则f'(x)=e,
k=eto
则
,则b=k-klnk,令h(k)=2k-klnk,则h'(k)=1-lnk,所以y=()在
eo=kxo+b
(0,e)上单调递增,在(e,+o)上单调递减,所以h(k)max=h(e)=e,即k+b的最大值为e.
另解:g(I)=k+b,即g(x)=c+b与f(x)=e“相切时,己知求g(I)的最大值,由图象可
知,g(x)=x+b与f(x)=e相切于点(l,e)时,k+b最大,即k+b的最大值为e.
高一期末检测数学参老答案第2页(共10页)
同课章节目录
