19．10 两点的距离公式

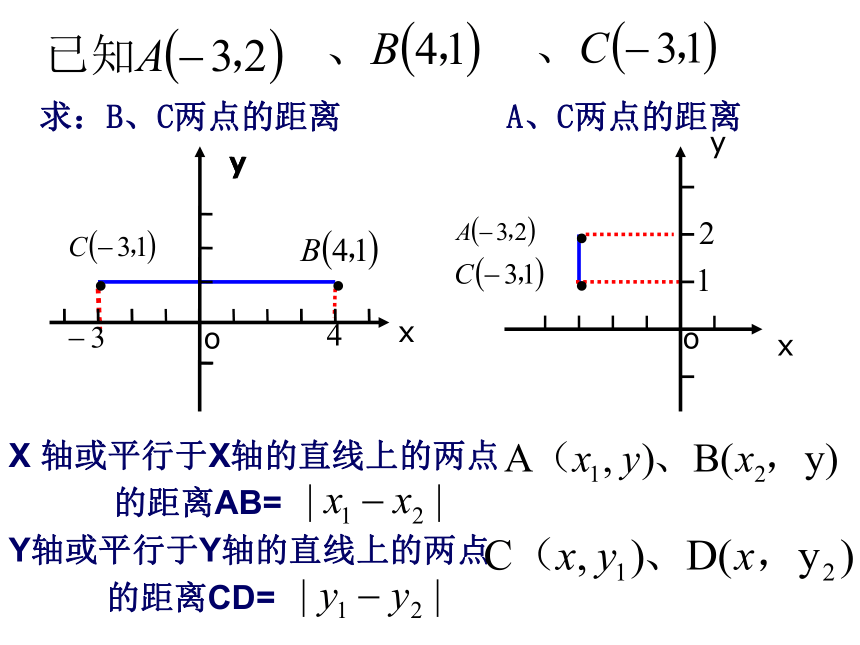
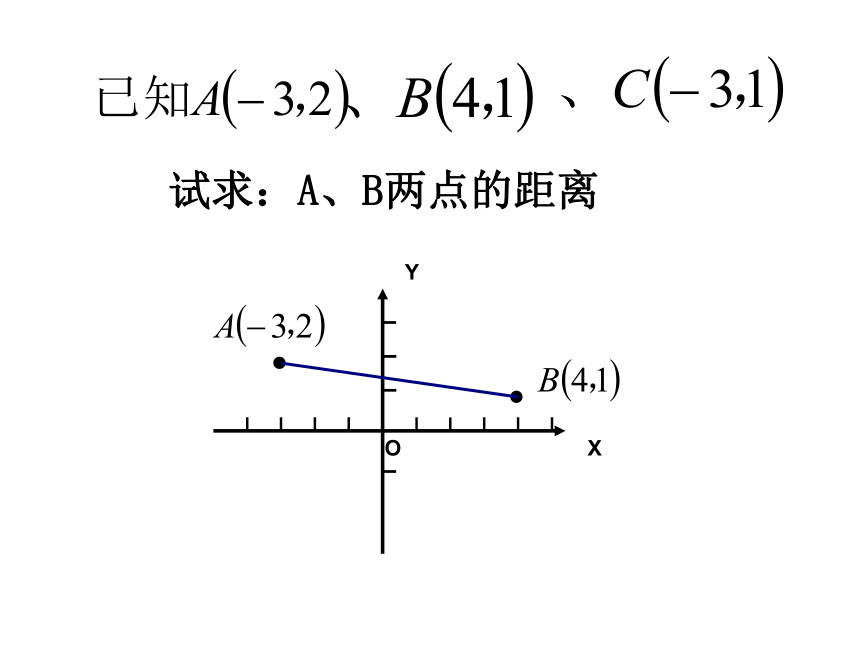
课件9张PPT。19.10两点的距离公式求：B、C两点的距离yA、C两点的距离yyoxyX 轴或平行于X轴的直线上的两点的距离AB=Y轴或平行于Y轴的直线上的两点的距离CD=试求：A、B两点的距离XYO已知平面直角坐标系内有两点如何求A、B 两点的距离？（AB与坐标轴不平行）练习
求下列两点的距离：
（1）A(1,2)和B(4,6) （2）C(-3,5)和D（7,-2）例1、已知坐标平面内的△ABC三个顶点A、B、C的坐标分别为A(-1,4)、B(-4,-2)、C(2,-5),判定这个三角形的形状？
XYOABC例2：已知直角坐标平面内的两点分别为A（3，3），B（6，1）
点P在X轴上，且PA=PB，求点P的坐标。 XYOABP变一变：
(2)点P在Y轴上，且PA = PB，求点P的坐标。小结：
1.在平面直角坐标系中，两点的距离公式。
2.在推导过程中通过构造直角三角形
利用勾股定理解决问题。
3.已知两点的坐标利用两点的距离公式
求两点的距离。
4.应用两点的距离公式求三角形的边长
并判断其形状。
5.根据两点的距离公式求满足某些条件的
点的坐标。（1）已知两点A（-3，1），B（1，4）在y轴上找一点C，使△ABC为等边三角形。拓展练习：（2）已知两点A（2，2），B（5，-2）试在X轴上求一点C，使△ABC为直角三角形。