八年级下册第19章 菱形的判定(课件)
文档属性
| 名称 | 八年级下册第19章 菱形的判定(课件) |

|
|
| 格式 | zip | ||
| 文件大小 | 767.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-02 00:00:00 | ||
图片预览





文档简介
课件19张PPT。19.2.2 菱形的判定 复习与回顾:想一想:
1.怎样判定一个四边形是平行四边形?
2.菱形、矩形的定义?
3.它们分别比平行四边形多了哪些性质?
4.怎样判定一个四边形是矩形? ?
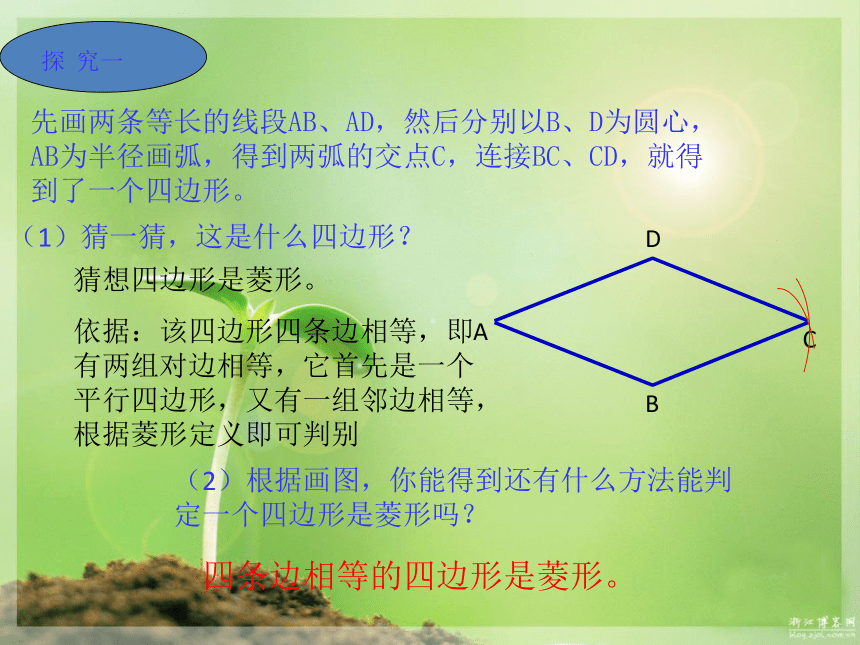
?矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形四条边都相等想一想 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.根据定义得:先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形。ACDB(2)根据画图,你能得到还有什么方法能判定一个四边形是菱形吗?猜想四边形是菱形。
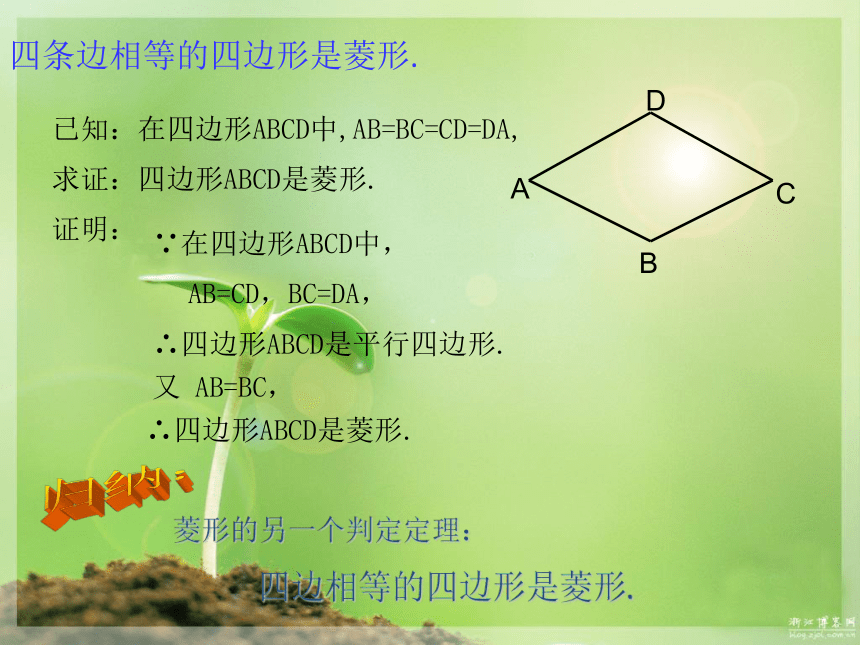
依据:该四边形四条边相等,即有两组对边相等,它首先是一个平行四边形,又有一组邻边相等,根据菱形定义即可判别四条边相等的四边形是菱形。(1)猜一猜,这是什么四边形?四条边相等的四边形是菱形.证明:∵在四边形ABCD中,归纳:菱形的另一个判定定理:
四边相等的四边形是菱形. AB=CD,BC=DA,∴四边形ABCD是平行四边形.又 AB=BC,∴四边形ABCD是菱形.探究二 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,当两木条互相垂直时,这个四边形像菱形吗?猜想:对角线互相垂直的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
O如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=∵ 四边形ABCD是平行四边形∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形).归纳菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.有四条边相等的四边形是菱形.2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。习题巩固:四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形新知初用证明:∵在□ABCD中
∴AE//FC
∴ ∠EAO= ∠OCF
∵EF平分AC,
∴OA=OC
又∵ ∠AOE= ∠COF=90o
∴ △AOE≌ △COF
∴OE=OF
∴四边形AFCE是平行四边形
又∵EF ⊥AC
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形)如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。习题演练:请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB借题发挥:DCBA作业1、课本P118习题19.2第1、2,3,4题2、一课一练、芝麻开花相关练习谢谢大家
1.怎样判定一个四边形是平行四边形?
2.菱形、矩形的定义?
3.它们分别比平行四边形多了哪些性质?
4.怎样判定一个四边形是矩形? ?
?矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形四条边都相等想一想 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.根据定义得:先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形。ACDB(2)根据画图,你能得到还有什么方法能判定一个四边形是菱形吗?猜想四边形是菱形。
依据:该四边形四条边相等,即有两组对边相等,它首先是一个平行四边形,又有一组邻边相等,根据菱形定义即可判别四条边相等的四边形是菱形。(1)猜一猜,这是什么四边形?四条边相等的四边形是菱形.证明:∵在四边形ABCD中,归纳:菱形的另一个判定定理:
四边相等的四边形是菱形. AB=CD,BC=DA,∴四边形ABCD是平行四边形.又 AB=BC,∴四边形ABCD是菱形.探究二 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,当两木条互相垂直时,这个四边形像菱形吗?猜想:对角线互相垂直的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
O如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=∵ 四边形ABCD是平行四边形∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形).归纳菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.有四条边相等的四边形是菱形.2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。习题巩固:四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形新知初用证明:∵在□ABCD中
∴AE//FC
∴ ∠EAO= ∠OCF
∵EF平分AC,
∴OA=OC
又∵ ∠AOE= ∠COF=90o
∴ △AOE≌ △COF
∴OE=OF
∴四边形AFCE是平行四边形
又∵EF ⊥AC
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形)如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。习题演练:请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB借题发挥:DCBA作业1、课本P118习题19.2第1、2,3,4题2、一课一练、芝麻开花相关练习谢谢大家
