八年级下册第19章 矩形、菱形与正方形 第三节 正方形(正方形的性质及其应用)课件
文档属性
| 名称 | 八年级下册第19章 矩形、菱形与正方形 第三节 正方形(正方形的性质及其应用)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 501.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-02 21:24:58 | ||
图片预览




文档简介
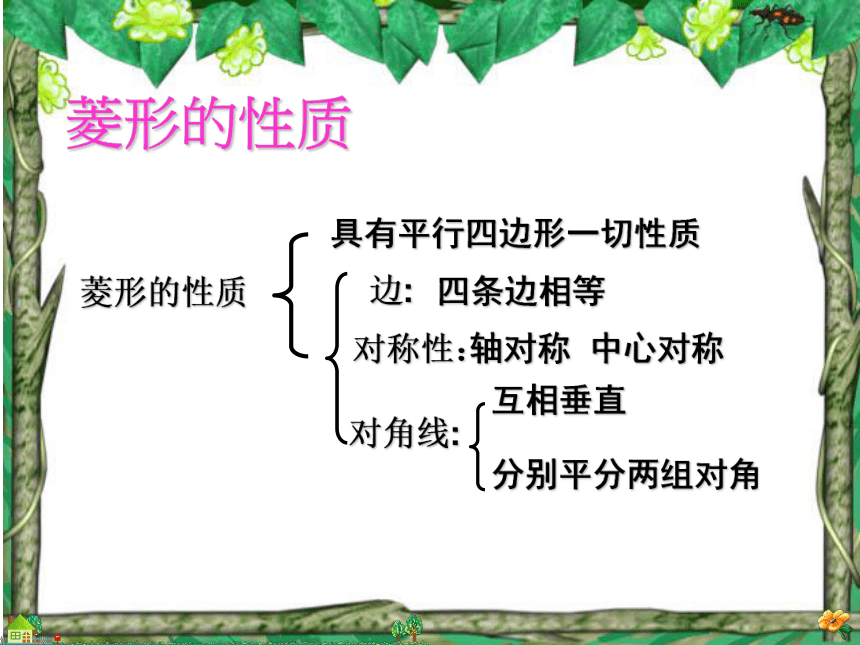
课件18张PPT。19.3 正方形的性质及应用复习回顾(1)平行四边形有哪些性质?矩形与平行四边形比较有哪些特殊的性质?平行四边形边:角:对角线:对边平行且相等对角相等对角线互相平分矩形角:四个角是直角对角线:对角线相等对称性:轴对称图形具有平行四边形一切性质菱形的性质菱形的性质边:四条边相等对角线:互相垂直分别平分两组对角轴对称 中心对称具有平行四边形一切性质对称性:该图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中有两个正方形.
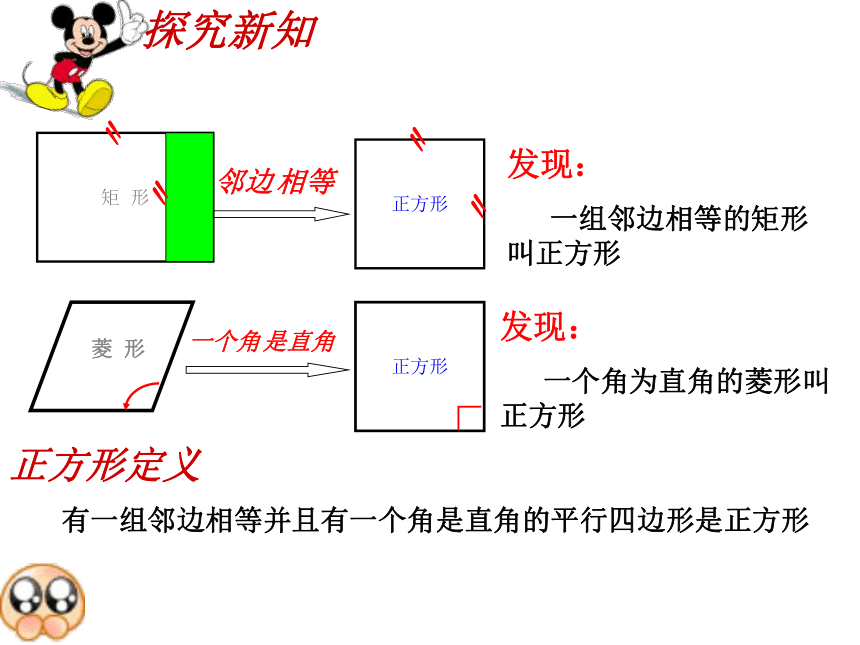
探究新知矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形 叫正方形一个角是直角正方形∟发现:
一个角为直角的菱形叫正方形正方形定义有一组邻边相等并且有一个角是直角的平行四边形是正方形平行四边形矩形菱形正
方
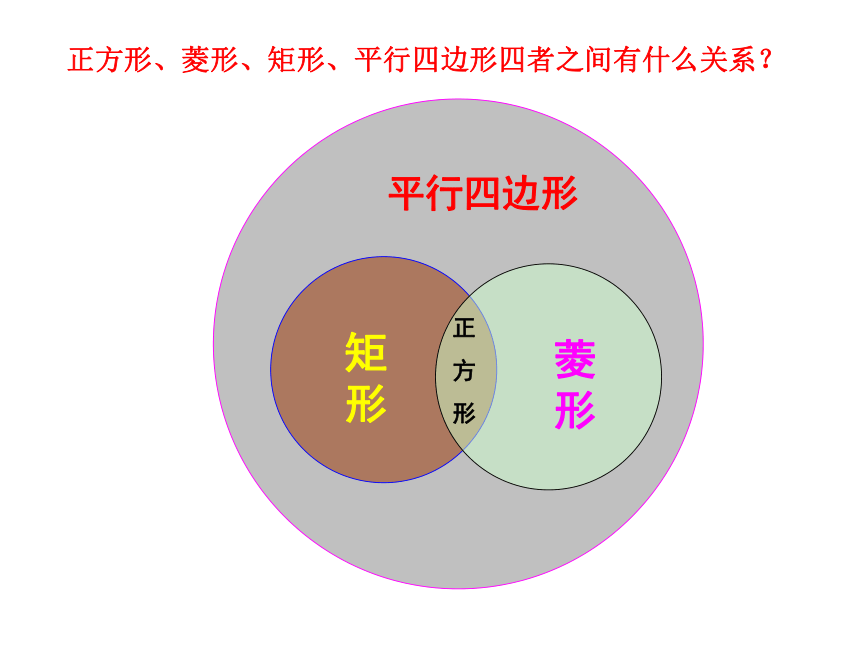
形正方形、菱形、矩形、平行四边形四者之间有什么关系?正方形的性质=你能说出正方形有哪些性质吗? 合作探究ACDBACDBACDB\∟∟∟∟O\\∟
对边平行, 四条边都相等 四 个 角
都是直角对角线互相垂直平分且相等,每条对角线平分一组对角∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD轴对称图形 中心对称图形ADCBO
正方形ABCD对角线相交于点O,图中共有多少个等腰直角三角形?找一找结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.(1)如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.53、填一填 (2)已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 224例1、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F. 请说明:EC=EF=FB证明:
∵ 四边形ABCD是正方形 ∴∠B=900 , ∠ACB=450
∵∠AEF=900 AB=AE
且AF=AF
∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900, ∠ECF=45°
∴∠EFC=45°
∴EC=EF(等角对等边)
∴BF=EF=EC
请你谈谈本节课有哪些收获感悟与收获 正方形的特征:
1.具有平行四边形的一切特征
两组对边平行且相等,两组对角相等,对角线互相平分
2.具有矩形的一切特征
四个角都是直角,对角线相等
3.具有菱形的一切特征
四条边都相等,对角线互相垂直且分别平分
4.既是中心对称图形,又是轴对称图形,有四条对称轴归纳1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。练一练已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF练一练、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (AAS)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°谢谢大家
探究新知矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形 叫正方形一个角是直角正方形∟发现:
一个角为直角的菱形叫正方形正方形定义有一组邻边相等并且有一个角是直角的平行四边形是正方形平行四边形矩形菱形正
方
形正方形、菱形、矩形、平行四边形四者之间有什么关系?正方形的性质=你能说出正方形有哪些性质吗? 合作探究ACDBACDBACDB\∟∟∟∟O\\∟
对边平行, 四条边都相等 四 个 角
都是直角对角线互相垂直平分且相等,每条对角线平分一组对角∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD轴对称图形 中心对称图形ADCBO
正方形ABCD对角线相交于点O,图中共有多少个等腰直角三角形?找一找结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.(1)如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.53、填一填 (2)已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 224例1、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F. 请说明:EC=EF=FB证明:
∵ 四边形ABCD是正方形 ∴∠B=900 , ∠ACB=450
∵∠AEF=900 AB=AE
且AF=AF
∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900, ∠ECF=45°
∴∠EFC=45°
∴EC=EF(等角对等边)
∴BF=EF=EC
请你谈谈本节课有哪些收获感悟与收获 正方形的特征:
1.具有平行四边形的一切特征
两组对边平行且相等,两组对角相等,对角线互相平分
2.具有矩形的一切特征
四个角都是直角,对角线相等
3.具有菱形的一切特征
四条边都相等,对角线互相垂直且分别平分
4.既是中心对称图形,又是轴对称图形,有四条对称轴归纳1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。练一练已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF练一练、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (AAS)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°谢谢大家
