1.4 《线段垂直平分线与角平分线》小节复习题(含详解)苏科版八年级数学上册
文档属性
| 名称 | 1.4 《线段垂直平分线与角平分线》小节复习题(含详解)苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 00:01:20 | ||
图片预览




文档简介
1.4 《线段垂直平分线与角平分线》小节复习题
题型01 线段垂直平分线的性质定理的运用(长度、角度)
1.如图,在 ABC中,,的垂直平分线分别交、于点D、E,的垂直平分线分别交、于点F、G,则的周长为( )
A.5 B.6 C.7 D.8
2.如图,在中,的垂直平分线交于点,的垂直平分线交于点若,则的度数是( )
A. B. C. D.
3.如图,中,,垂直平分,交于点F,交于点E,且.若 ABC周长为13,, .
4.如图,在 ABC中,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线交于点D,连接,若,,则的周长为( )
A.17 B.16 C.18 D.20
题型02 线段垂直平分线的判定定理及运用
1.如图,已知:,,点E在的延长线上.(1)求证:垂直平分;(2)求证: BDE
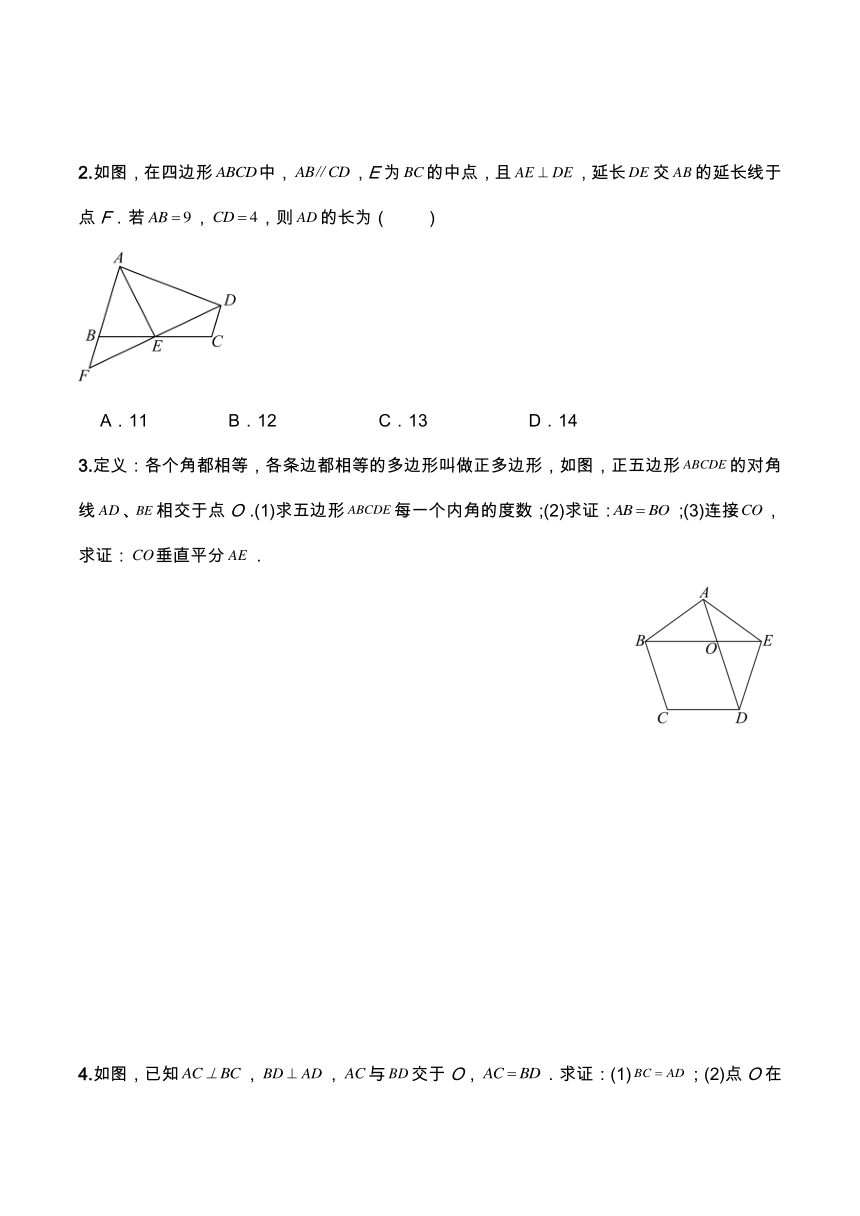
2.如图,在四边形中,,E为的中点,且,延长交的延长线于点F.若,,则的长为( )
A.11 B.12 C.13 D.14
3.定义:各个角都相等,各条边都相等的多边形叫做正多边形,如图,正五边形的对角线、相交于点O.(1)求五边形每一个内角的度数;(2)求证:;(3)连接,求证:垂直平分.
4.如图,已知,,与交于O,.求证:(1);(2)点O在线段的垂直平分线上.
题型03 角平分线性质定理的运用(长度、面积、角度)
1.如图,点是 ABC内一点,平分,于点,连接,若,,则 AOB的面积是( )
A. B. C. D.
2.如图,平分,于点,,,则的长为( )
A. B. C. D.
3.如图,在中,,的平分线交于点,为上一动点,则的最小值为( )
A.2 B. C. D.2.5
4.如图,在 ABC中,,是内一点,过点作于点,于点于点,若,则的度数为( )
A. B. C. D.
题型04 角平分线的判定定理的运用
1.如图,在 ABC中,点E、F分别在上,是的垂直平分线,,,交于点G.
(1)求证:平分;(2)若,求证:.
2.如图,在 ABC中,D是延长线上一点,与的角平分线交于点E,连接.若要求的度数,只需要知道下列哪个角的度数( )
A. B. C. D.
3.如图, ABC中,点、分别是、延长线上一点,、的角平分线、交于点,连接,过点作、,垂足分别是点、,则、、之间的数量关系是 .
4.如图,与都是等边三角形,若与相交于点.
(1)求的度数;(2)连接,求证:平分.
题型05 角平分线的第二定理(拓展)
1.已知 ABC,是一条角平分线.
(1)【探究发现】如图1所示,若是的角平分线.可得到结论:.
小红的解法如下:过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴________.(________)
∴________,又∵,∴.
(2)【类比探究】如图2所示,若是的外角平分线,与的延长线交于点.求证:.
(3)【拓展应用】如图3所示,在 ABC中,,、分别是、的角平分线且相交于点,若,直接写出的值是________.
2.如图, ABC的三边、、长分别是、、,其三条角平分线交于点,并将 ABC分为三个三角形,则的比值为( )
A. B. C. D.
3.某数学兴趣小组进行如下探究:如图1,在 ABC中,是它的中线,则中线平分三角形的面积,即.继续探究,如图2,在 ABC中,是它的角平分线,此时角平分线不一定平分三角形的面积,但发现和的面积比等于图中两组不同的线段比,即①________,②________.
(1)【证明结论】①根据“发现”,完成填空:________=________;
②请选择“发现”中的一组线段比进行证明.
(2)【应用结论】如图3,在 ABC中,是它的角平分线,,是的中点,连接.①求证:垂直平分;②在图中画出边上的高(只需体现的位置),并求.
4.已知 ABC,是一条角平分线.
【探究发现】如图1,若是的角平分线.可得到结论:.
小艳的解法如下:过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴______
∴______又∵,∴______
【类比探究】如图2,若是的外角平分线,与的延长线交于点.求证:.
【拓展应用】如图3,在 ABC中,,、分别是、的角平分线且相交于点,若,直接写出的值是______
题型06 多定理叠加运用(垂直平分线+角平分线)
1.如图,在 ABC中,为的中点,交的平分线于,于,交延长线于.(1)求证:.(2)猜想、、的数量有什么关系?并证明你的猜想;(3)若,,则________.
2.如图,已知是线段的垂直平分线,直线经过点,过点作,垂足是,点是线段上一点,连接,,平分,则线段之间的等量关系是 .
3.如图, ABC 中,的角平分线和边的垂直平分线交于点,的延长线于点 , 于点. 若,,则的长为( )
A. B. C. D.
4.如图,已知 ABC中边上的垂直平分线与的平分线交于点E,交的延长线于点F,交于点G.(1)求证:.(2)求证:.
题型07 线段垂直平分线与角平分线的实际应用
1.如图,某小区的三栋单元楼分别位于 ABC的三个顶点处,要在 ABC内建一个快递站,并使快递站到每一栋单元楼的距离相等,则快递站应建在 ABC的( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高所在直线的交点 D.三条中线的交点
2.如图,是三条直线表示三条相互交叉的公路,现要建一个中转站,要求它到三条公路交叉点的距离都相等,则可供选择的地址有( ).
A.一处 B.两处 C.三处 D.四处
3.如图,直线 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
4.某镇准备在两两相交的三条公路围成的三角形空地上建一个物流园,使其到三条公路的距离相等,请问物流园所建位置应是( )
A.三角形三条角平分线的交点 B.三角形三边垂直平分线的交点
C.三角形三条中线的交点 D.三角形三条高的交点
题型08 线段垂直平分线与角平分线的尺规作图
1.如图,A、B两镇位于国道l的同侧,两镇距离国道分别有数公里.随着经济发展,过往车辆增多,政府规划在国道l上新建一座多功能加油站,既为车辆提供便利,又促进两镇资源互通.如果你是工程师,请解决以下规划问题:
(1)公平选址:确定加油站位置P,使得加油站到A、B两镇的距离相等;
(2)路径优化:从A镇前往B镇,需途径加油站加油.确定加油站位置Q,使得总路程最短:请分别作出上述两种情况下的加油站P、Q的位置.(要求:尺规作图,保留作图痕迹并写出结论,不用证明)
2.如图,已知 ABC,以下是小聪通过尺规作图解决问题的部分过程:
①以点B为圆心,任意长为半径画弧,分别交于点E,F;②以点E为圆心,长为半径画弧,两弧交于点M;③作射线,与延长线父于点P,点D为延长线上一点.
根据以上作法,下列结论不成立的是( )
A. B. C. D.
3.尺规作图:求作点P,使点P到点M,N的距离相等,同时到的两边的距离也相等.
4.如图,两条笔直的小路与相交于点,点、处分别为枫叶林景区和花卉景区,现打算在内部修建一处观景台,使得观景台到的距离与观景台到的距离相等.且,请你找出观景台的位置.(尺规作图,保留作图痕迹,不写作法)
5.尺规作图:如图, ABC中,为上一点,连接 ,请在 ABC内部找一点 . 使点到边的距离相等,且满足(保留作图痕迹,不写作法)
题型09 角平分线的性质与判定综合运用
1.如图,在 ABC中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则.其中正确的个数是( )
A.个 B.个 C.个 D.个
2.如图,为的角平分线,,过作于,交的延长线于,则下列结论:①;②;③;④;其中正确结论的序号有( )
A.①②③ B.①②④ C.②③④ D.①②③④
3.如图,在 ABC中,,平分交于点,平分交于点,交于点.则下列说法正确的个数为( )
①;②;③若,则;④;⑤
A.2个 B.3个 C.4个 D.5个
4.如图,在 ABC中,,,,,角平分线、交于点,于点,.下列结论:①点在的平分线上;②;③;④,其中正确的结论是 (填序号)
5.如图,在 ABC中,,角平分线、交于点O,于点F.下列结论:①;②;③;④若,则,其中正确结论有 .
题型10 线段垂直平分线的判定与性质的综合运用
1.如图,在 ABC中,是边上的高,是的角平分线,垂直平分,垂足为点H,分别交于点,交的延长线于点M,连结;下列结论:①;②;③;④.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图, ABC中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
3.情景一:小明在数学兴趣小组探究活动课上发现:对于一个△ABC,分别作边AB,AC的垂直平分线DM,EN相交于点O,如图1所示,此时经过测量后,得到∠MAN=30°,根据上述条件,能不能得到∠BAC的度数呢?小明结合所学过的知识进行了以下论证.
证明:∵DM是边AB的垂直平分线,
∴MA=MB,∴∠MAB=∠B.同理可得∠NAC=∠C,
则 解得∠BAC=105°.
情景二:小明继续对上述问题进行探究发现:若边AB,AC的垂直平分线DM,EN相交于点O,如图2所示,试判断∠MAN与∠BAC之间的数量关系.
(1)情景一中得到∠MAB=∠B的理由是______.
(2)在图1的情况下,若∠MAN的度数为α,则∠BAC的大小为______(用含α的代数式表示).
(3)请写出情景二中∠MAN与∠BAC之间的数量关系,并说明理由.
4.如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O.
(1)如图1,当时,直接写出的度数_________;
(2)如图1,当,且.
①若,则________°;②当_________°时,;
(3)如图2,连接,,.若 ADE的周长为,的周长为.则线段________;线段__________.(4)如图3,若,则__________°.
参考答案
题型01 线段垂直平分线的性质定理的运用(长度、角度)
1.C
【详解】解:∵垂直平分,垂直平分,∴,,
∴的周长为,故选:C.
2.C
【详解】解:,,
的垂直平分线交于点,的垂直平分线交于点,
,,,,
,,故选:C.
3.
【详解】解:∵是的垂直平分线,∴.
∵,∴是的垂直平分线,∴,∴.
∵ ABC的周长为,,∴,∴,
则,∴,即.故答案为:.
4.D
【详解】解:由作图痕迹可得,垂直且平分,,
,故选:D.
题型02 线段垂直平分线的判定定理及运用
1.(1)证明:∵,,∴点A和D都在线段的垂直平分线上,∴垂直平分;
(2)证明:由(1)知垂直平分,∴,
在 BDE和中,,∴.
2.C
【详解】解:为的中点,,
,,,
在与中,,,
,,,
,,,故选:C.
3.(1)解:由题意得:;
(2)证明:,,
同理得:,,
,,;
(3)证明:连接,,,,,∴,,
,,垂直平分.
4.(1)证明:∵,,∴,
∴在和中,,∴,∴;
(2)证明:∵,∴,∴,
∴点O在线段的垂直平分线上.
题型03 角平分线性质定理的运用(长度、面积、角度)
1.C
【详解】解:过O作于点E,∵平分,,∴,
∴ AOB的面积,故选:C.
2.A
【详解】解:如图,过点作于点,
∵平分,,,∴,
∵,,∴,∴.故选:A.
3.A
【详解】解:作于H,如图,
∵的平分线交于点,,,∴,
∵Q为上一动点,∴的最小值为的长,即的最小值为2.故选:B.
4.D
【详解】解:∵点作于点,于点于点,,
∴分别平分,∴,
∵,∴,
∴,∴;故选D.
题型04 角平分线的判定定理的运用
1.(1)证明:∵是的垂直平分线,∴,
∵,,∴平分;
(2)解:∵,∴,
∵是的垂直平分线,∴,∴,∴,
∴,,∴,∴.
2.C
【详解】解:作于点,于点,交的延长线于点,
∵与的角平分线交于点E,∴,∴,∴平分,
∴,∴只需要知道的度数即可求出的度数;故选C.
3.
【详解】解:如下图所示,过点作,平分,、,,
又平分,,,平分,,
在和中,,,同理可证,,,故答案为: .
4.(1)解:与都是等边三角形,
,,,,
在和 BDE中,,,,
;
(2)证明:连接,作,于点,,如图所示:
,,,,
,平分.
题型05 角平分线的第二定理(拓展)
1.(1)过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴,(角平分线的性质)
∴,又∵,∴.
(2)如图,过点D作于N,过点D作于M,过点A作于点P,
是的外角平分线,即平分,,
,又,.
(3)在上取点G,使得,连接,
、分别是、的角平分线且相交于点,,
,,,
在 BDE和中,,,
,,
,平分,,
在和中,,,,
,由(1)可得,在中,为的角平分线,,
设,则,,,
2.A
【详解】解:过点作,,,垂足分别为,,,
∵ ABC的三条角平分线交于点O,,,,,
.故选:A.
3.(1)解:①根据“发现”,完成填空:,
②选择:在 ABC中,是它的角平分线,点D到和的距离相等,
即中边上的高,和中边上的高相等,设为h,则;
选择:点D在上,点D到和的距离相等,
即中边上的高,和中边上的高相等,设为,则;
(2)解:①证明:,,由(1)得,,
是的中点,,,又是的角平分线,垂直平分;
②如图,即为所求;
延长交的延长线于点G,设,,
由①得,,
是的角平分线,,,,
在和中,,,
,,,
由①得,,,,
,,.
4.探究发现:解:过点作于点,于点,过点作于点,
∵是的角平分线,且,,
∴,∴,又∵,∴;
故答案为:,,;
类比探究:
证明:过点D作交延长线于N,过点D作延长线于M,过点C作于点P.
∵平分,∴.
∴,,∴;
拓展应用:在上取点G,使得,连接,
∵,∴,∵分别是的角平分线,
∴,,,
∴,∴,∵,∴,
∴,∴∴是的角平分线
由(1)知,,设,,则,,
由(1)知,即.
题型06 多定理叠加运用(垂直平分线+角平分线)
1.(1)证明:如图,连接、,∵,D为中点,∴,
∵,,且平分,∴,
在和中,,∴,∴;
(2)解:,证明如下:在和中,
,∴,∴,由(1)知,
∴.即;
(3)解:由(2)知,∵,,∴,
∴,∴,故答案为:2.
2.
【详解】解:如图,过点作于,连接,
∵,∴,∵平分,∴,
在和中,,∴,∴,,
∵,,∴,
∵是的一个外角,∴,∴,
即,∴,
∵是的垂直平分线,∴,∴,∴,
又∵,,∵,
在和中,,,∴,
∴,∴,故答案为:.
3.B
【详解】解:连接
∵是的平分线 ,∴,∵,,∴,
在和中 ,,∴,∴,,
∵是的垂直平分线,∴,
在和中 ,,∴,∴,
∵,,∴,∴,故选:.
4.(1)证明:连接和,∵是的垂直平分线,∴,
∵平分,,,∴,,
在和中,, ∴,∴;
(2)证明:∵平分,,,∴,,
在和中, ,∴,∴,
∵,∴,即.
题型07 线段垂直平分线与角平分线的实际应用
1.B
【详解】解:∵快递站到每一栋单元楼的距离相等,∴快递站应建在的三边的垂直平分线的交点处.
故选B.
2.A
【详解】解:如图所示,分别作,,的垂直平分线,则三条垂直平分线的交点P即为可供选择的地址,有1处.故选:A.
3.D
【详解】解:如图所示,根据角平分线的性质定理“角平分线上点到角两边的距离相等”得到点到三条公里的距离相等,∴可供选择的地址有4个,故选:D .
4.A
【详解】解:∵角平分线上的点到角两边的距离相等,
∴物流园需建在三条公路所围成三角形的角平分线的交点上.故选A.
题型08 线段垂直平分线与角平分线的尺规作图
1.(1)如图所示,点P即为所求;
(2)解;如图所示,点Q即为所求;
2.C
【详解】解:连接,过点作于点,于点,
由作图得,,又,∴,∴,
∴,故选项A正确,不符合题意;
∵,∴,
∴,故选项B正确,不符合题意;无法判断,故选项C符合题意;
∵,,,∴,又,
∴,故选项D正确,不符合题意;故选:C.
3.解:如图:点P即为所求.
4.解:如图,作线段的垂直平分线,作的平分线,与的垂直平分线交于点,点即为所求.∵观景台到的距离与观景台到的距离相等,∴点在的角平分线上,
∵,∴点在线段的垂直平分线上,
∴的角平分线于线段的垂直平分线上的交点即为点.
5.解:点到边的距离相等, P点在的角平分线上;
,,点P在的垂直平分线上;
点P为的角平分线与的垂直平分线的交点,如图所示,点P为所求.
题型09 角平分线的性质与判定综合运用
1.B
【详解】解:和的平分线相交于点,,,
,①错误;
,,,分别是与的平分线,
,,,,
如图,在上取一点,使,是的角平分线,,
在和中,,,
,,,
在和中,,,
,,故②正确;作于,于,
和的平分线相交于点,
点在的平分线上,,,
,故③正确.故选:B.
2.A
【详解】解:∵平分,,,∴,
在和中,,∴,故①正确;∴,
在和中,,∴,
∴,∴,故②正确;
∵,∴,设交于,
∵,∴,故③正确;
∵,,∴,
∵,∴,
∵,∴,∴,
又∵,∴,
∴,即,
∵,∴,
∵,∴,
∵,∴,∵和不一定相等,
∴和不一定相等,∴和不一定相等,故④错误;
综上,正确结论的序号有①②③,故选:.
3.C
【详解】解:设,,
平分交于点,平分交于点,,
,,,;
在中,,故①说法正确,符合题意;
是的角平分线,不是三角形的中线,与不一定相等,故与不一定相等,
故②说法错误,不符合题意;若,则,
∵平分,∴,∴,,
,故③说法正确,符合题意;如图1所示,在边上取,连接,
平分,,,,,
∵,,,
又平分,∴,,
,,,故④说法正确,符合题意;
过作于,于,∵,∴,
∵,,,
故⑤说法正确,符合题意;综上,说法正确的有①③④⑤,共4个.故选:C.
4.①②④
【详解】解:过点O作于点G,于点N,如图所示:
∵是的角平分线,,,∴,
同理得:,∴,∴点在的平分线上,故①正确;
在 ABC中,,,∵BD,CE分别是的角平分线,
,,
,则,结论②正确;
如图,在上取一点,使得,连接,连接,
在和中,,,
,,
由对顶角相等得:,,
在和中,,,,,
,,
在和中,,,,
在和中,,,,
∴,故③错误;由以上证明可知:,
∴,故④正确;综上,正确的结论是①②④,故答案为:①②④.
5.①③
【详解】解:如图,过点作于点,
∵是的角平分线,,∴,
∵,,∴,结论①正确;
∵,,∴,∴,
∵是的角平分线,∴,∴,
∵,∴,结论②错误;
如图,过点作于点,作于点,
∵是的角平分线,是的角平分线,,
∴,,,
∵,∴,
∴,∴,
∵,,∴,
在和中,,∴,∴,结论③正确;
如图,在取一点,使得,连接,
∵是的角平分线,是的角平分线,∴,,
在和中,,∴,∴,,
由上已证:,∴,∴,即,
在和中,,∴,∴,
设,∵,∴,∴,
∴,
又∵,∴,∴,
∴,
∴,结论④错误;综上,正确结论有①③,故答案为:①③.
题型10 线段垂直平分线的判定与性质的综合运用
1.D
【详解】解:,,,,
,,所以①正确;
是的角平分线,,
,而,
,所以②正确;
垂直平分,,,
,,,所以③正确;
,,所以④正确.
故选:D.
2.C
【详解】①∵将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),
∴直线垂直平分,故①正确;
②由①得,直线垂直平分,∴,,
∴∠NAD=∠NDA,,∴
∵是 CDM的一个外角,是 NAD的一个外角,
∴,
∴,∴,
∴,∴,∴
又∵,∴
即,
又∵(已证),∴,故②正确;
③∵,∴,∴
又∵,∴与不一定相等,
∴与不一定相等,∴与不一定相等,故③错误;
④∵是的中点,∴,∵,∴,∴,,
又,∴,∴,
∴,故④正确;综上所述,一定正确的有①②④,故选:C.
3.(1)解:是的垂直平分线,,
,(SAS),,故答案为:;
(2)由(1)知,,同理可得,,
,,
,故答案为:;
(3)∠MAN+2∠BAC=180°;
理由:是的垂直平分线,,
,,同理可得,,
,,
,,
,,.
4.(1)解:∵垂直平分,垂直平分,∴,,
∴,,
∴;故答案为:.
(2)解:①∵,∴,
∵垂直平分,垂直平分,∴,,
∴,,∴,
∴;故答案为:60;
②∵,∴,根据解析①可知,,
∵,∴,
∴,即当时,;故答案为:135.
(3)解:根据解析(2)可知,,,
∵ ADE的周长为,∴,∴,即,
∵垂直平分,垂直平分,∴,,∴,
∵的周长为,∴,∴,
解得:.故答案为:9;6.
(4)解:∵,∴,
∵垂直平分,垂直平分,∴,,
∴,,∴,
∴,
∵,∴.故答案为:36。
题型01 线段垂直平分线的性质定理的运用(长度、角度)
1.如图,在 ABC中,,的垂直平分线分别交、于点D、E,的垂直平分线分别交、于点F、G,则的周长为( )
A.5 B.6 C.7 D.8
2.如图,在中,的垂直平分线交于点,的垂直平分线交于点若,则的度数是( )
A. B. C. D.
3.如图,中,,垂直平分,交于点F,交于点E,且.若 ABC周长为13,, .
4.如图,在 ABC中,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线交于点D,连接,若,,则的周长为( )
A.17 B.16 C.18 D.20
题型02 线段垂直平分线的判定定理及运用
1.如图,已知:,,点E在的延长线上.(1)求证:垂直平分;(2)求证: BDE
2.如图,在四边形中,,E为的中点,且,延长交的延长线于点F.若,,则的长为( )
A.11 B.12 C.13 D.14
3.定义:各个角都相等,各条边都相等的多边形叫做正多边形,如图,正五边形的对角线、相交于点O.(1)求五边形每一个内角的度数;(2)求证:;(3)连接,求证:垂直平分.
4.如图,已知,,与交于O,.求证:(1);(2)点O在线段的垂直平分线上.
题型03 角平分线性质定理的运用(长度、面积、角度)
1.如图,点是 ABC内一点,平分,于点,连接,若,,则 AOB的面积是( )
A. B. C. D.
2.如图,平分,于点,,,则的长为( )
A. B. C. D.
3.如图,在中,,的平分线交于点,为上一动点,则的最小值为( )
A.2 B. C. D.2.5
4.如图,在 ABC中,,是内一点,过点作于点,于点于点,若,则的度数为( )
A. B. C. D.
题型04 角平分线的判定定理的运用
1.如图,在 ABC中,点E、F分别在上,是的垂直平分线,,,交于点G.
(1)求证:平分;(2)若,求证:.
2.如图,在 ABC中,D是延长线上一点,与的角平分线交于点E,连接.若要求的度数,只需要知道下列哪个角的度数( )
A. B. C. D.
3.如图, ABC中,点、分别是、延长线上一点,、的角平分线、交于点,连接,过点作、,垂足分别是点、,则、、之间的数量关系是 .
4.如图,与都是等边三角形,若与相交于点.
(1)求的度数;(2)连接,求证:平分.
题型05 角平分线的第二定理(拓展)
1.已知 ABC,是一条角平分线.
(1)【探究发现】如图1所示,若是的角平分线.可得到结论:.
小红的解法如下:过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴________.(________)
∴________,又∵,∴.
(2)【类比探究】如图2所示,若是的外角平分线,与的延长线交于点.求证:.
(3)【拓展应用】如图3所示,在 ABC中,,、分别是、的角平分线且相交于点,若,直接写出的值是________.
2.如图, ABC的三边、、长分别是、、,其三条角平分线交于点,并将 ABC分为三个三角形,则的比值为( )
A. B. C. D.
3.某数学兴趣小组进行如下探究:如图1,在 ABC中,是它的中线,则中线平分三角形的面积,即.继续探究,如图2,在 ABC中,是它的角平分线,此时角平分线不一定平分三角形的面积,但发现和的面积比等于图中两组不同的线段比,即①________,②________.
(1)【证明结论】①根据“发现”,完成填空:________=________;
②请选择“发现”中的一组线段比进行证明.
(2)【应用结论】如图3,在 ABC中,是它的角平分线,,是的中点,连接.①求证:垂直平分;②在图中画出边上的高(只需体现的位置),并求.
4.已知 ABC,是一条角平分线.
【探究发现】如图1,若是的角平分线.可得到结论:.
小艳的解法如下:过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴______
∴______又∵,∴______
【类比探究】如图2,若是的外角平分线,与的延长线交于点.求证:.
【拓展应用】如图3,在 ABC中,,、分别是、的角平分线且相交于点,若,直接写出的值是______
题型06 多定理叠加运用(垂直平分线+角平分线)
1.如图,在 ABC中,为的中点,交的平分线于,于,交延长线于.(1)求证:.(2)猜想、、的数量有什么关系?并证明你的猜想;(3)若,,则________.
2.如图,已知是线段的垂直平分线,直线经过点,过点作,垂足是,点是线段上一点,连接,,平分,则线段之间的等量关系是 .
3.如图, ABC 中,的角平分线和边的垂直平分线交于点,的延长线于点 , 于点. 若,,则的长为( )
A. B. C. D.
4.如图,已知 ABC中边上的垂直平分线与的平分线交于点E,交的延长线于点F,交于点G.(1)求证:.(2)求证:.
题型07 线段垂直平分线与角平分线的实际应用
1.如图,某小区的三栋单元楼分别位于 ABC的三个顶点处,要在 ABC内建一个快递站,并使快递站到每一栋单元楼的距离相等,则快递站应建在 ABC的( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高所在直线的交点 D.三条中线的交点
2.如图,是三条直线表示三条相互交叉的公路,现要建一个中转站,要求它到三条公路交叉点的距离都相等,则可供选择的地址有( ).
A.一处 B.两处 C.三处 D.四处
3.如图,直线 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
4.某镇准备在两两相交的三条公路围成的三角形空地上建一个物流园,使其到三条公路的距离相等,请问物流园所建位置应是( )
A.三角形三条角平分线的交点 B.三角形三边垂直平分线的交点
C.三角形三条中线的交点 D.三角形三条高的交点
题型08 线段垂直平分线与角平分线的尺规作图
1.如图,A、B两镇位于国道l的同侧,两镇距离国道分别有数公里.随着经济发展,过往车辆增多,政府规划在国道l上新建一座多功能加油站,既为车辆提供便利,又促进两镇资源互通.如果你是工程师,请解决以下规划问题:
(1)公平选址:确定加油站位置P,使得加油站到A、B两镇的距离相等;
(2)路径优化:从A镇前往B镇,需途径加油站加油.确定加油站位置Q,使得总路程最短:请分别作出上述两种情况下的加油站P、Q的位置.(要求:尺规作图,保留作图痕迹并写出结论,不用证明)
2.如图,已知 ABC,以下是小聪通过尺规作图解决问题的部分过程:
①以点B为圆心,任意长为半径画弧,分别交于点E,F;②以点E为圆心,长为半径画弧,两弧交于点M;③作射线,与延长线父于点P,点D为延长线上一点.
根据以上作法,下列结论不成立的是( )
A. B. C. D.
3.尺规作图:求作点P,使点P到点M,N的距离相等,同时到的两边的距离也相等.
4.如图,两条笔直的小路与相交于点,点、处分别为枫叶林景区和花卉景区,现打算在内部修建一处观景台,使得观景台到的距离与观景台到的距离相等.且,请你找出观景台的位置.(尺规作图,保留作图痕迹,不写作法)
5.尺规作图:如图, ABC中,为上一点,连接 ,请在 ABC内部找一点 . 使点到边的距离相等,且满足(保留作图痕迹,不写作法)
题型09 角平分线的性质与判定综合运用
1.如图,在 ABC中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则.其中正确的个数是( )
A.个 B.个 C.个 D.个
2.如图,为的角平分线,,过作于,交的延长线于,则下列结论:①;②;③;④;其中正确结论的序号有( )
A.①②③ B.①②④ C.②③④ D.①②③④
3.如图,在 ABC中,,平分交于点,平分交于点,交于点.则下列说法正确的个数为( )
①;②;③若,则;④;⑤
A.2个 B.3个 C.4个 D.5个
4.如图,在 ABC中,,,,,角平分线、交于点,于点,.下列结论:①点在的平分线上;②;③;④,其中正确的结论是 (填序号)
5.如图,在 ABC中,,角平分线、交于点O,于点F.下列结论:①;②;③;④若,则,其中正确结论有 .
题型10 线段垂直平分线的判定与性质的综合运用
1.如图,在 ABC中,是边上的高,是的角平分线,垂直平分,垂足为点H,分别交于点,交的延长线于点M,连结;下列结论:①;②;③;④.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图, ABC中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
3.情景一:小明在数学兴趣小组探究活动课上发现:对于一个△ABC,分别作边AB,AC的垂直平分线DM,EN相交于点O,如图1所示,此时经过测量后,得到∠MAN=30°,根据上述条件,能不能得到∠BAC的度数呢?小明结合所学过的知识进行了以下论证.
证明:∵DM是边AB的垂直平分线,
∴MA=MB,∴∠MAB=∠B.同理可得∠NAC=∠C,
则 解得∠BAC=105°.
情景二:小明继续对上述问题进行探究发现:若边AB,AC的垂直平分线DM,EN相交于点O,如图2所示,试判断∠MAN与∠BAC之间的数量关系.
(1)情景一中得到∠MAB=∠B的理由是______.
(2)在图1的情况下,若∠MAN的度数为α,则∠BAC的大小为______(用含α的代数式表示).
(3)请写出情景二中∠MAN与∠BAC之间的数量关系,并说明理由.
4.如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O.
(1)如图1,当时,直接写出的度数_________;
(2)如图1,当,且.
①若,则________°;②当_________°时,;
(3)如图2,连接,,.若 ADE的周长为,的周长为.则线段________;线段__________.(4)如图3,若,则__________°.
参考答案
题型01 线段垂直平分线的性质定理的运用(长度、角度)
1.C
【详解】解:∵垂直平分,垂直平分,∴,,
∴的周长为,故选:C.
2.C
【详解】解:,,
的垂直平分线交于点,的垂直平分线交于点,
,,,,
,,故选:C.
3.
【详解】解:∵是的垂直平分线,∴.
∵,∴是的垂直平分线,∴,∴.
∵ ABC的周长为,,∴,∴,
则,∴,即.故答案为:.
4.D
【详解】解:由作图痕迹可得,垂直且平分,,
,故选:D.
题型02 线段垂直平分线的判定定理及运用
1.(1)证明:∵,,∴点A和D都在线段的垂直平分线上,∴垂直平分;
(2)证明:由(1)知垂直平分,∴,
在 BDE和中,,∴.
2.C
【详解】解:为的中点,,
,,,
在与中,,,
,,,
,,,故选:C.
3.(1)解:由题意得:;
(2)证明:,,
同理得:,,
,,;
(3)证明:连接,,,,,∴,,
,,垂直平分.
4.(1)证明:∵,,∴,
∴在和中,,∴,∴;
(2)证明:∵,∴,∴,
∴点O在线段的垂直平分线上.
题型03 角平分线性质定理的运用(长度、面积、角度)
1.C
【详解】解:过O作于点E,∵平分,,∴,
∴ AOB的面积,故选:C.
2.A
【详解】解:如图,过点作于点,
∵平分,,,∴,
∵,,∴,∴.故选:A.
3.A
【详解】解:作于H,如图,
∵的平分线交于点,,,∴,
∵Q为上一动点,∴的最小值为的长,即的最小值为2.故选:B.
4.D
【详解】解:∵点作于点,于点于点,,
∴分别平分,∴,
∵,∴,
∴,∴;故选D.
题型04 角平分线的判定定理的运用
1.(1)证明:∵是的垂直平分线,∴,
∵,,∴平分;
(2)解:∵,∴,
∵是的垂直平分线,∴,∴,∴,
∴,,∴,∴.
2.C
【详解】解:作于点,于点,交的延长线于点,
∵与的角平分线交于点E,∴,∴,∴平分,
∴,∴只需要知道的度数即可求出的度数;故选C.
3.
【详解】解:如下图所示,过点作,平分,、,,
又平分,,,平分,,
在和中,,,同理可证,,,故答案为: .
4.(1)解:与都是等边三角形,
,,,,
在和 BDE中,,,,
;
(2)证明:连接,作,于点,,如图所示:
,,,,
,平分.
题型05 角平分线的第二定理(拓展)
1.(1)过点作于点,于点,过点作于点,
∵是的角平分线,且,,∴,(角平分线的性质)
∴,又∵,∴.
(2)如图,过点D作于N,过点D作于M,过点A作于点P,
是的外角平分线,即平分,,
,又,.
(3)在上取点G,使得,连接,
、分别是、的角平分线且相交于点,,
,,,
在 BDE和中,,,
,,
,平分,,
在和中,,,,
,由(1)可得,在中,为的角平分线,,
设,则,,,
2.A
【详解】解:过点作,,,垂足分别为,,,
∵ ABC的三条角平分线交于点O,,,,,
.故选:A.
3.(1)解:①根据“发现”,完成填空:,
②选择:在 ABC中,是它的角平分线,点D到和的距离相等,
即中边上的高,和中边上的高相等,设为h,则;
选择:点D在上,点D到和的距离相等,
即中边上的高,和中边上的高相等,设为,则;
(2)解:①证明:,,由(1)得,,
是的中点,,,又是的角平分线,垂直平分;
②如图,即为所求;
延长交的延长线于点G,设,,
由①得,,
是的角平分线,,,,
在和中,,,
,,,
由①得,,,,
,,.
4.探究发现:解:过点作于点,于点,过点作于点,
∵是的角平分线,且,,
∴,∴,又∵,∴;
故答案为:,,;
类比探究:
证明:过点D作交延长线于N,过点D作延长线于M,过点C作于点P.
∵平分,∴.
∴,,∴;
拓展应用:在上取点G,使得,连接,
∵,∴,∵分别是的角平分线,
∴,,,
∴,∴,∵,∴,
∴,∴∴是的角平分线
由(1)知,,设,,则,,
由(1)知,即.
题型06 多定理叠加运用(垂直平分线+角平分线)
1.(1)证明:如图,连接、,∵,D为中点,∴,
∵,,且平分,∴,
在和中,,∴,∴;
(2)解:,证明如下:在和中,
,∴,∴,由(1)知,
∴.即;
(3)解:由(2)知,∵,,∴,
∴,∴,故答案为:2.
2.
【详解】解:如图,过点作于,连接,
∵,∴,∵平分,∴,
在和中,,∴,∴,,
∵,,∴,
∵是的一个外角,∴,∴,
即,∴,
∵是的垂直平分线,∴,∴,∴,
又∵,,∵,
在和中,,,∴,
∴,∴,故答案为:.
3.B
【详解】解:连接
∵是的平分线 ,∴,∵,,∴,
在和中 ,,∴,∴,,
∵是的垂直平分线,∴,
在和中 ,,∴,∴,
∵,,∴,∴,故选:.
4.(1)证明:连接和,∵是的垂直平分线,∴,
∵平分,,,∴,,
在和中,, ∴,∴;
(2)证明:∵平分,,,∴,,
在和中, ,∴,∴,
∵,∴,即.
题型07 线段垂直平分线与角平分线的实际应用
1.B
【详解】解:∵快递站到每一栋单元楼的距离相等,∴快递站应建在的三边的垂直平分线的交点处.
故选B.
2.A
【详解】解:如图所示,分别作,,的垂直平分线,则三条垂直平分线的交点P即为可供选择的地址,有1处.故选:A.
3.D
【详解】解:如图所示,根据角平分线的性质定理“角平分线上点到角两边的距离相等”得到点到三条公里的距离相等,∴可供选择的地址有4个,故选:D .
4.A
【详解】解:∵角平分线上的点到角两边的距离相等,
∴物流园需建在三条公路所围成三角形的角平分线的交点上.故选A.
题型08 线段垂直平分线与角平分线的尺规作图
1.(1)如图所示,点P即为所求;
(2)解;如图所示,点Q即为所求;
2.C
【详解】解:连接,过点作于点,于点,
由作图得,,又,∴,∴,
∴,故选项A正确,不符合题意;
∵,∴,
∴,故选项B正确,不符合题意;无法判断,故选项C符合题意;
∵,,,∴,又,
∴,故选项D正确,不符合题意;故选:C.
3.解:如图:点P即为所求.
4.解:如图,作线段的垂直平分线,作的平分线,与的垂直平分线交于点,点即为所求.∵观景台到的距离与观景台到的距离相等,∴点在的角平分线上,
∵,∴点在线段的垂直平分线上,
∴的角平分线于线段的垂直平分线上的交点即为点.
5.解:点到边的距离相等, P点在的角平分线上;
,,点P在的垂直平分线上;
点P为的角平分线与的垂直平分线的交点,如图所示,点P为所求.
题型09 角平分线的性质与判定综合运用
1.B
【详解】解:和的平分线相交于点,,,
,①错误;
,,,分别是与的平分线,
,,,,
如图,在上取一点,使,是的角平分线,,
在和中,,,
,,,
在和中,,,
,,故②正确;作于,于,
和的平分线相交于点,
点在的平分线上,,,
,故③正确.故选:B.
2.A
【详解】解:∵平分,,,∴,
在和中,,∴,故①正确;∴,
在和中,,∴,
∴,∴,故②正确;
∵,∴,设交于,
∵,∴,故③正确;
∵,,∴,
∵,∴,
∵,∴,∴,
又∵,∴,
∴,即,
∵,∴,
∵,∴,
∵,∴,∵和不一定相等,
∴和不一定相等,∴和不一定相等,故④错误;
综上,正确结论的序号有①②③,故选:.
3.C
【详解】解:设,,
平分交于点,平分交于点,,
,,,;
在中,,故①说法正确,符合题意;
是的角平分线,不是三角形的中线,与不一定相等,故与不一定相等,
故②说法错误,不符合题意;若,则,
∵平分,∴,∴,,
,故③说法正确,符合题意;如图1所示,在边上取,连接,
平分,,,,,
∵,,,
又平分,∴,,
,,,故④说法正确,符合题意;
过作于,于,∵,∴,
∵,,,
故⑤说法正确,符合题意;综上,说法正确的有①③④⑤,共4个.故选:C.
4.①②④
【详解】解:过点O作于点G,于点N,如图所示:
∵是的角平分线,,,∴,
同理得:,∴,∴点在的平分线上,故①正确;
在 ABC中,,,∵BD,CE分别是的角平分线,
,,
,则,结论②正确;
如图,在上取一点,使得,连接,连接,
在和中,,,
,,
由对顶角相等得:,,
在和中,,,,,
,,
在和中,,,,
在和中,,,,
∴,故③错误;由以上证明可知:,
∴,故④正确;综上,正确的结论是①②④,故答案为:①②④.
5.①③
【详解】解:如图,过点作于点,
∵是的角平分线,,∴,
∵,,∴,结论①正确;
∵,,∴,∴,
∵是的角平分线,∴,∴,
∵,∴,结论②错误;
如图,过点作于点,作于点,
∵是的角平分线,是的角平分线,,
∴,,,
∵,∴,
∴,∴,
∵,,∴,
在和中,,∴,∴,结论③正确;
如图,在取一点,使得,连接,
∵是的角平分线,是的角平分线,∴,,
在和中,,∴,∴,,
由上已证:,∴,∴,即,
在和中,,∴,∴,
设,∵,∴,∴,
∴,
又∵,∴,∴,
∴,
∴,结论④错误;综上,正确结论有①③,故答案为:①③.
题型10 线段垂直平分线的判定与性质的综合运用
1.D
【详解】解:,,,,
,,所以①正确;
是的角平分线,,
,而,
,所以②正确;
垂直平分,,,
,,,所以③正确;
,,所以④正确.
故选:D.
2.C
【详解】①∵将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),
∴直线垂直平分,故①正确;
②由①得,直线垂直平分,∴,,
∴∠NAD=∠NDA,,∴
∵是 CDM的一个外角,是 NAD的一个外角,
∴,
∴,∴,
∴,∴,∴
又∵,∴
即,
又∵(已证),∴,故②正确;
③∵,∴,∴
又∵,∴与不一定相等,
∴与不一定相等,∴与不一定相等,故③错误;
④∵是的中点,∴,∵,∴,∴,,
又,∴,∴,
∴,故④正确;综上所述,一定正确的有①②④,故选:C.
3.(1)解:是的垂直平分线,,
,(SAS),,故答案为:;
(2)由(1)知,,同理可得,,
,,
,故答案为:;
(3)∠MAN+2∠BAC=180°;
理由:是的垂直平分线,,
,,同理可得,,
,,
,,
,,.
4.(1)解:∵垂直平分,垂直平分,∴,,
∴,,
∴;故答案为:.
(2)解:①∵,∴,
∵垂直平分,垂直平分,∴,,
∴,,∴,
∴;故答案为:60;
②∵,∴,根据解析①可知,,
∵,∴,
∴,即当时,;故答案为:135.
(3)解:根据解析(2)可知,,,
∵ ADE的周长为,∴,∴,即,
∵垂直平分,垂直平分,∴,,∴,
∵的周长为,∴,∴,
解得:.故答案为:9;6.
(4)解:∵,∴,
∵垂直平分,垂直平分,∴,,
∴,,∴,
∴,
∵,∴.故答案为:36。
同课章节目录
