2025新苏科版七年级数学上册第二章有理数知识点讲解及练习题(含解析)
文档属性
| 名称 | 2025新苏科版七年级数学上册第二章有理数知识点讲解及练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 20:06:08 | ||
图片预览




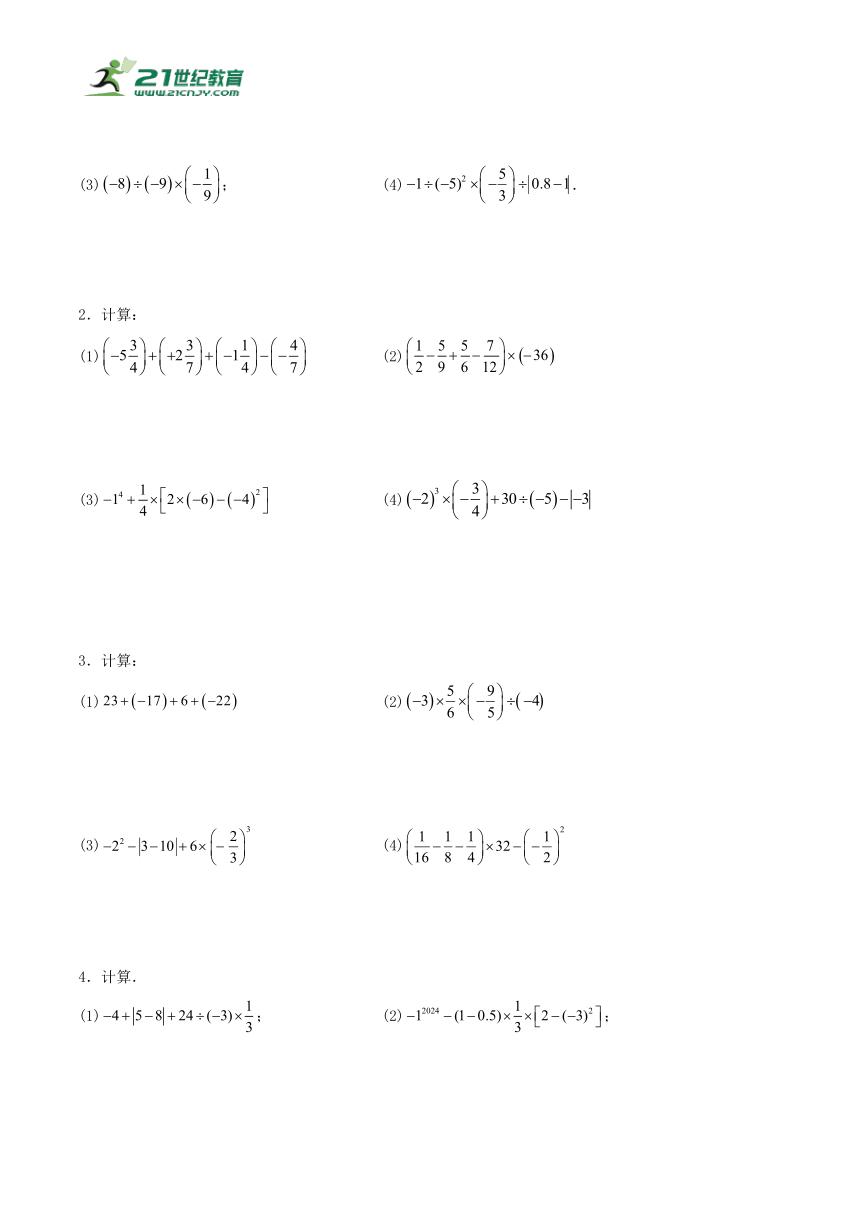
文档简介
2025新苏科版七年级数学上册第二章有理数知识点讲解及练习题
知识点
知识点1:正数与负数意义
1.具有相反意义的量包括三个要素:具有同类性;具有相反意义;具有数量。
2.正数、负数可以表示两个相反意义的量。
知识点2:有理数及其分类
有理数的概念:有理数是整数和分数的统称。
有理数的四种表现形式:整数、分数、有限小数、无限循环小数。判断一个数是不是有理数,只要看看这个数是不是这四种就行了,如果是这四种中一个,那这个数一定是有理数;如果不是这四种中的任何一种,那它一定不是有理数。
有理数的分类方法:
(1)按概念分类: (2)按正负分类:
知识点3:数轴
1.数轴是规定了原点,正方向,单位长度的直线。
2.数轴的三要素:原点,正方向,单位长度。
知识点4:有理数的大小比较方法
有理数的大小关系:
对于两个有理数,下列三种关系有且仅有一种成立:。
有理数的大小关系的比较方法:方法1:借助数轴比较;方法2:借助绝对值比较。
4.有理数的大小关系具有传递性:
(1)如果,那么就有。(2)如果,那么就有。
知识点5:绝对值与相反数
1.绝对值的定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2.绝对值的表示方法:数a的绝对值记作|a|.
3.绝对值的代数意义:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.即对于任何有理数a都有:
4.绝对值的几何意义:
一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小.
的几何意义:数轴上表示数的点到原点的距离。
5.绝对值的性质:非负性,即任何一个数的绝对值总是正数或0即
6.相反数的定义:只有符号不同的两个数互为相反数;0的相反数是0.
7.相反数的表示方法:的相反数为。
8.相反数的性质:
(1)位置关系:互为相反数的两数的点分别位于原点的两旁,且与原点的距离相等.
(2)和的关系:互为相反数的两数和为0.
知识点6:有理数的加法法则
1.加法法则
加数类型 加法法则 典型范例
同号两数相加 同号两数相加,取相同的符号,并把绝对值相加;
异号两数相加 异号两数相加,绝对值相等时,和为0
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值
一数与0相加 一个数同0相加,仍得这个数
知识点7:有理数的加法运算律
1.加法运算律:
(1)加法交换律:
(2)加法结合律:
名师点拨:
(1)加法运算律的作用:简化运算,凑整,凑同号;
(2)交换加数的位置时,不要忘记符号.
知识点8:有理数的减法法则
有理数减法法则:减去一个数,等于加这个数的相反数,即有:.
名师点拨:
(1)将减法转化为加法时,注意“两变”,一变是减号变加号;二变是把减数变为它的相反数”.
(2)灵活使用减法法则,比较熟练的同学也可以不按步骤,直接写结果,提高效率。
知识点9:有理数的乘法法则
有理数的乘法法则:
(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
名师点拨:
(1)不为0的两数相乘,先定符号,再把绝对值相乘.
(2)当乘数中有负数时,必须用括号括起来:
如5与-3的乘积,应列为5×(-3),不应该写成5×-3.
2.有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积相等,
即:.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
即:.
(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
即:.
知识点10:有理数的除法法则
1.有理数除法法则:
(1)法则1:除以一个不等于0的数,等于乘这个数的倒数,即。
(2)法则2:两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
2. 倒数的概念: 乘积是1的两个数互为倒数.
名师点拨:
(1)0不能当除数;
(2)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.
知识点11:有理数的乘方
1.乘方的概念:求相同因数的积的运算,叫做乘方,乘方的结果叫做幂(power).
即有:.
底数:在中,叫做底数,
指数:叫做指数.
典型例子:此处2叫做底数,3是指数,表示2的个数;
2.特例:当指数=2时,一般成为平方;当指数=3时,一般成为立方。
知识点12:科学记数法(这是一个很小,但非常非常重要的知识点,要牢记)
科学记数法的定义:
把一个绝对值大于10的数表示成的形式(其中l≤||<10,是正整数),这种记数法叫做科学记数法.
名师点拨:
(1)负数也可以用科学记数法表示,“”照写,其它与正数一样;
(2)把一个数写成形式时,若这个数是大于10的数,则n比这个数的整数位数少1.
知识点13:有理数的混合运算
1.有理数的混合运算顺序:(混合运算三原则)
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2.合理运用运算律简化运算
1.加法运算律:
加法交换律:
加法结合律:
2.乘法交换律:
乘法交换律:
乘法结合律:
乘法分配律:
3.灵活选用适当的运算律,可以简化计算,减少错误。运用乘法分配率时要根据自己的基础情况选用。
典型例题
教材习题第66页复习题第7(3)题 计算: 解题方法指导 解法1:直接通分计算 解法2:可以使用分配率计算
【分析】 解法1:直接通分计算 解法1:直接通分计算
教材习题69页复习题探索研究第18题 如果的绝对值和相等,那么满足什么条件? 如果的绝对值比大,那么满足什么条件? 解题方法指导 举出各种类型的数,比如负数,0,正数,通过对特例的研究,发现其中的规律; 从特殊到一般是我们研究一些较难问题的一般方法
【分析】 先举出一些特殊的各种类型的数,进行研究判断: 第(1)题:为正数时,发现 为负数时,发现,不符合题意 时,,发现 总结:当为非负数时,。 第(2)题:可以采用类似的方法解决: 根据上题可以知道,为正数时 ,不符合题意; 为负数时,发现,符合题意 时,,发现,不符合题意 总结:当为负数时,。
题型训练
题型1 有理数的混合运算问题
1.计算:
(1); (2);
(3); (4).
2.计算:
(1) (2)
(3) (4)
3.计算:
(1) (2)
(3) (4)
4.计算.
(1); (2);
(3); (4).
5.解决下列问题:
(1); (2);
(3); (4).
题型2 有理数简便运算
简便运算:
简便计算:.
简便计算:;
4.用简便方法计算:
(1) ; (2) .
5.简便计算:
(1) (2)
题型3 有理数混合运算的新定义问题
1.对于任意有理数a,b,我们定义一种新运算“”,规定:,如:.
(1)求的值;
(2)求的值.
2.我们定义一种新运算:.例如:.
(1)求的值;
(2)求的值.
3.若定义一种新的运算“”,规定有理数,如.
(1)求的值;
(2)求的值.
4.定义新运算:当时,;当时,;当其中,是实数,如.计算:
(1);
(2).
5.定义一种新的运算:,如:,
求:
(1);
(2).
题型4 与有理数混合运算有关的程序图问题
1.嘉琪同学在自学了简单的电脑编程后,设计了如图所示的程序.
(1)若开始输入为,请你根据程序列出算式并计算出输出结果;
(2)嘉琪发现将一个小于的数输入,得到的结果总是正数.请验证这个结论.
2.小鹏做了一个如图所示的程序图,按要求完成下列各小题.
(1)当小鹏输入的数为6时,求输出的结果n;
(2)若小鹏某次输入数m后,输出的结果n为.请你写出m可能的2个值.
3.有三种运算程序如下图所示,按要求完成下列各题:
(1)如图,当输入数时,输出数_____;
(2)如图,第一个带?号的运算框内,应填_____;第二个带?号的运算框内,应填_____;第三个带?号的运算框内,应填_____.
(3)如图,当输入时,则输出结果为_____.
4.按照如图和图所示的程序,进行计算.
(1)如果输入,求输出结果;
(2)若在图基础上增加一个计算程序“”,如图,重新输入,第一次运算得到,求输出结果.
5.如图所示、淇淇做了一个程序图,按要求完成下列问题.
(1)当淇淇输入的数为6时,则输出的结果
(2)若淇淇某次输入数m后,输出的结果n为,请你写出m的两个可能值
题型5 有理数混合运算的实际应用
1.南部县是一座历史文化悠久、人口众多的大县,出租车是重要的交通工具,出租车的计价标准为:行程不超过2千米收费5元,超过2千米的部分按每千米1.5元收费(不足1千米的按1千米计算)一出租车公司坐落于南北方向的南铁大道边,驾驶员张师傅从公司出发,在此大道上连续接送5批客人,行驶记录如下:(注;一批次的客人指的是一次可坐1到4位客人,规定向北为正,向南为负,单位:千米)
第一批 第二批 第三批 第四批 第五批
(1)送完第五批客人后,张师傅在公司的 边(填南或北)距离公司 千米的位置.
(2)张师傅的车平均每千米消耗压缩天然气0.09升,则送完第五批客人后,张师傅用了多少升压缩天然气?
(3)在整个过程中,张师傅共收到车费多少元?
2.科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富,小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负,下表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克)
(1)求小王第一周销售柚子最多的一天比最少的一天多销售多少千克.
(2)求小王第一周实际销售柚子的总量是多少千克?
(3)若小王按8元/千克进行柚子销售,平均运费为2元/千克,则小王第一周销售柚子一共收入多少元?
3.某仓库原有商品件,现记录了天内该类商品进出仓库的件数如下所示(“”表示进库,“”表示出库):,,,,,,,,,.
(1)请问经过天之后,该仓库内的商品是增加了还是减少了?此时仓库还有多少商品?
(2)如果商品每次进出仓库需要人工搬运费是每件元,请问这天要付多少人工搬运费?
4.为巩固脱贫攻坚成果,助力乡村振兴快速发展.我县所略乡推行“发展茶油产业,加快脱贫的步伐”.某种植户新鲜采摘了20筐茶果,以每筐25千克为标准重量,超过或不足千克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:千克) 0 1
筐数 1 4 2 3 2 8
(1)与标准重量比较,20筐茶果总计超过或不足多少千克?
(2)若该种植户采摘生茶果每千克售价元,则出售这20筐茶果可获得多少元?
5.正值中秋佳节,小梦和妈妈一块去购买月饼,妈妈买了一盒某品牌月饼共计8枚.小梦将8枚月饼的质量称重后统计表如下(单位:克):
第枚 1 2 3 4 5 6 7 8
质量 56 55 54.8 56.2 55.3 55.3 54.7 54.3
(1)小梦为了简化运算,选取了一个恰当的标准质量,依据这个标准质量,小梦把超出的部分记为正,不足的部分记为负,列出表格(不完整).请根据表格计算这个标准质量_______克,下面表格中第3枚月饼的质量是________克;
第枚 1 2 3 4 5 6 7 8
质量 ________ ________ ________ ________ ________
当小梦看到说明书上标记的总质量为克时,小梦妈妈买的月饼在总质量上是否合格?请你通过计算说明为什么.
过关训练
一、选择题
1.下面两个量中,不具有相反意义的是( )
A.盈利和亏损元 B.浪费水和节约水
C.进三个球和输三场比赛 D.上升和下降
2.下列四个数中,属于负数的是( )
A.1.2 B.1 C. D.0
3.在,,0,1.2,2,中,非负整数有( )
A.1个 B.2个 C.3个 D.4个
4.下列各图中,数轴表示正确的是( )
A. B.
C. D.
5.在数轴上,表示有理数a,b的点的位置如图所示,把个数按照从小到大的顺序排列,正确的是( )
A. B. C. D.
6.2025的相反数是( )
A. B. C. D.2025
7.的绝对值是( )
A. B. C. D.2
8.算筹我国是最早认识负数并进行相关运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用算筹(小棍形状的记数工具)来表示正负数,其中正放表示正数,斜放表示负数,例如图①表示的是的运算过程.按照这种方法,可推算图②中的算式为( )
A. B.
C. D.
9.比低的温度是( )
A. B. C. D.
10.如果,,那么下列成立的是( )
A., B., C., D.,
二、填空题
11.数轴上与点2相距3个单位长度的点表示的数为 .
12.比较大小: (填“”或“”)
13.计算: .
14. ,
15.计算:(1) ;
(2) .
16.若,,,则的绝对值是 .
17.的倒数是 .
18.华为最新款手机芯片“麒麟990”是一种微型处理器,每秒可进行次运算,用科学记数法表示为
19.定义一种新运算:,则 .
20.根据流程图中的程序,若输入x的值为,则输出y的值为 .
三、解答题
21.计算:
(1);
(2).
22.计算:
(1);
(2).
23.探究规律,完成相关题目.
定义“*”运算:
;
;
;
;
;
;
;
;
;
.
归纳*运算的法则(用文字语言叙述)
(1)绝对值不同的两数进行*运算时,结果的绝对值如何确定?_________.
特别地,0和任何数进行*运算,或任何数和0进行*运算,_____.
(2)计算:
(3)是否存在两个非零有理数m,n,使得,若存在,求出m,n满足的关系,若不存在,请说明理由.
24.一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A地出发,晚上最后到达B地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题:
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)
25.最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加,小明家新换了一辆新能源汽车,他连续7天记录了每天行驶的路程(如表).以为标准,多于的记为“+”,不足的记为“-”,刚好的记为“”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程()
(1)这天里路程最多的一天比最少的一天多走______km;(答案直接填写在答题卡的横线上)
(2)请求出小明家的新能源汽车这七天一共行驶了多少千米?
(3)小明家原来的汽油车每行驶需用汽油升,汽油价元/升.现在的新能源汽车每行驶耗电量为度,每度电为元.请估计小明家换成新能源汽车后这天的行驶费用比原来节省多少钱?
答案解析
题型练习
题型1 有理数的混合运算问题
1.计算:
(1); (2);
(3); (4).
【答案】(1)1
(2)
(3)
(4)
【分析】本题考查有理数的含有乘方的混合运算.解题关键是熟练掌握运算法则是解题的关键.
(1)有理数的加减运算法则计算即可;
(2)根据乘法分配律计算即可;
(3)将除法转化为乘法,根据乘法计算即可;
(4)先算乘方和绝对值,再算乘除法,再算加法
【详解】(1)解:
;
(2)解:
+
;
(3)解:
;
(4)解:
;
2.计算:
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查的是求一个数的绝对值,加法的运算律,乘法的运算律,含乘方的有理数的混合运算,掌握有理数加减乘除,乘方运算的运算法则与运算顺序是解题的关键.
(1)利用加法的运算律,把分母相同的两个数先加,从而可得答案;
(2)利用乘法的分配律把原式化为:,再计算乘法,最后计算加减运算即可;
(3)先计算括号内的运算,同步计算乘方运算,再计算乘法运算,最后计算加减运算即可;
(4)先计算乘方运算,同步计算除法与绝对值,再计算乘法运算,最后计算加减运算即可.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
3.计算:
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查了有理数的混合运算;
(1)利用加法交换律和结合律进行计算,即可解答;
(2)利用乘法分配律进行计算,即可解答;
(3)先算乘方,再算乘除,后算加减,即可解答;
(4)先算乘方,再算乘法,后算加减,有括号先算括号里,即可解答.
【详解】(1)解:
;
(2)解:
;
(3)解:
(4)解:
4.计算.
(1);
(2);
(3);
(4).
【答案】(1)
(2)
(3)2
(4)15
【分析】本题考查了有理数的四则混合运算和含乘方的有理数的混合运算,熟练掌握运算法则和顺序是解题的关键.
(1)先计算绝对值和有理数的乘除,再计算有理数的加减,即得答案;
(2)先计算有理数的乘方,然后计算两个括号中的加减,再计算有理数的乘法,最后计算有理数的加减,即得答案.
(3)先算括号,再算除法即可;
(4)先算乘方,再算乘除,最后算加减即可.
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
5.解决下列问题:
(1);
(2);
(3);
(4).
【答案】(1)3
(2)
(3)3
(4)
【分析】本题考查了有理数的混合运算,熟练掌握运算法则是解答本题的关键.
(1)把减法统一成加法,再按加法法则计算;
(2)利用乘法分配律计算即可;
(3)先算乘方,再算除法,后算加减;
(4)先算乘方、除法、绝对值,再算乘法,后算加减
【详解】(1)解:
(2)解:
(3)解:
(4)解:
题型2 有理数简便运算
简便运算:
【答案】
【分析】本题主要考查了含乘方的有理数混合计算,有理数乘法分配律,先把原式变形为,再利用乘法结合律变形得到,据此利用乘法分配律求解即可.
【详解】解:
.
简便计算:.
【答案】25
【分析】本题主要考查了含乘方的有理数混合运算、有理数乘法运算律的简便运算等知识点,掌握相关运算法则和运算律成为解题的关键.
运用有理数的乘法运算律进行简便运算即可.
【详解】解:
.
简便计算:;
【答案】
【分析】先确定积的符号,再逆用乘法分配律进行简便运算即可;
【详解】解:
;
4.用简便方法计算:
(1) ; (2) .
【答案】(1)
(2)
【分析】(1)把改写成,把改写成,然后把除法转化为乘法,再按乘法分配律计算即可;
(2)先算乘方,然后把一、四项结合,二、三项结合,逆用乘法分配律计算.
【详解】(1)解:原式
.
(2)解:原式
.
5.简便计算:
(1) (2)
【答案】(1);(2)
【分析】(1)根据逆用乘法分配率进行计算即可;
(2)先计算括号内的,再根据乘法分配律简便运算即可.
【详解】(1)
(2)
题型3 有理数混合运算的新定义问题
1.对于任意有理数a,b,我们定义一种新运算“”,规定:,如:.
(1)求的值;
(2)求的值.
【答案】(1)49;
(2)109.
【分析】本题主要考查了有理数的混合运算,理解新定义是解题的关键.
(1)直接根据新定义的法则,结合有理数的相应的运算法则进行运算即可.
(2)先根据新定义计算,再计算即可求解.
【详解】(1)解:
.
所以的值为49.
(2)解:
;
.
所以的值为109.
2.我们定义一种新运算:.例如:.
(1)求的值;
(2)求的值.
【答案】(1)1
(2)4
【分析】本题主要考查了新定义,含乘方的有理数混合计算:
(1)根据新定义得到,据此代值计算即可;
(2)根据新定义得到,再根据,进行计算求解即可.
【详解】(1)解:由题意得:
;
(2)解:
.
3.若定义一种新的运算“”,规定有理数,如.
(1)求的值;
(2)求的值.
【答案】(1)21
(2)40
【分析】本题考查了新定义和有理数的混合运算,正确理解新定义和有理数的运算法则解题的关键.
(1)按照新定义法则把原式转化为有理数运算,再计算即可;
(2)按照新定义法则把原式转化为有理数运算,再计算即可.
【详解】(1)解:;
(2)解:,
∴.
4.定义新运算:当时,;当时,;当其中,是实数,如.计算:
(1);
(2).
【答案】(1)
(2).
【分析】()根据新定义列出算式,然后根据运算法则即可求解;
()根据新定义列出算式,然后根据运算法则即可求解;
本题考查了有理数的混合运算,熟练掌握运算法则是解题的关键.
【详解】(1)
解:
;
(2)
解:
,
则
.
5.定义一种新的运算:,如:,
求:
(1);
(2).
【答案】(1)
(2)
【分析】此题考查了新定义运算和有理数的混合运算,弄清题中的新定义是解本题的关键.
(1)把原式利用题中的新定义计算转换为有理数运算,即可得到结果;
(2)先计算,求得,再计算,即可得到结果.
【详解】(1)解:由题意得:
;
(2)解:由题意得:
.
题型4 与有理数混合运算有关的程序图问题
1.嘉琪同学在自学了简单的电脑编程后,设计了如图所示的程序.
(1)若开始输入为,请你根据程序列出算式并计算出输出结果;
(2)嘉琪发现将一个小于的数输入,得到的结果总是正数.请验证这个结论.
【答案】(1);
(2)见解析
【分析】本题主要考查了有理数的混合运算,不等式的性质,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(1)首先用开始输入的数乘,求出积是多少;然后用所得的积除以2,求出商是多少;最后用所得的商减去即可.
(2)这个数是x,得出程序的结果为,再令,代入验证即可.
【详解】(1)解:
;
(2)解:设这个数是x,则,
,
,
,即得到的结果总是正数.
2.小鹏做了一个如图所示的程序图,按要求完成下列各小题.
(1)当小鹏输入的数为6时,求输出的结果n;
(2)若小鹏某次输入数m后,输出的结果n为.请你写出m可能的2个值.
【答案】(1)
(2)或0.5
【分析】本题考查程序流程图与有理数运算:
(1)根据流程图,列出算式进行计算即可;
(2)分或两种情况进行讨论求解即可.
【详解】(1)解:当时,,
,
,
,
;
(2),
当时,,
当时,;
故m可能为或0.5.
3.有三种运算程序如下图所示,按要求完成下列各题:
(1)如图,当输入数时,输出数_____;
(2)如图,第一个带?号的运算框内,应填_____;第二个带?号的运算框内,应填_____;第三个带?号的运算框内,应填_____.
(3)如图,当输入时,则输出结果为_____.
【答案】(1)
(2),,
(3)
【分析】(1)利用图中公式计算得出答案;
(2)利用最后的代数式推出空格中的式子;
(3)根据图中计算公式及判断条件分别计算得出答案.
【详解】(1)解:如图,当输入数时,输出数,
故答案为:;
(2)解:第一个带?号的运算框内,应填:,
第二个带?号的运算框内,应填:,
第三个带?号的运算框内,应填:,
故答案为:,,;
(3)解:,
,
,
,
,
,
,
,
,
输出结果为:,
故答案为:.
【点睛】本题主要考查了程序流程图与有理数计算,有理数四则混合运算,代数式表示的实际意义,程序流程图与代数式求值等知识点,看懂程序流程图并得出正确信息是解题的关键.
4.按照如图和图所示的程序,进行计算.
(1)如果输入,求输出结果;
(2)若在图基础上增加一个计算程序“”,如图,重新输入,第一次运算得到,求输出结果.
【答案】(1);
(2).
【分析】本题主要考查了流程图,有理数的混合运算,解分式方程等知识点,根据流程图正确列式是解题的关键.
()根据程序中的运算法则列式计算即可;
()根据程序中的运算法则列出分式方程,求出的值,再根据运算法则列式计算即可.
【详解】(1)解:
;
(2)解:,
,
∴,
经检验,是原分式方程的解,
∴
.
5.如图所示、淇淇做了一个程序图,按要求完成下列问题.
(1)当淇淇输入的数为6时,则输出的结果
(2)若淇淇某次输入数m后,输出的结果n为,请你写出m的两个可能值
【答案】 ,(答案不唯一)
【分析】本题考查程序流程图和有理数的运算,按照程序流程图准确的进行计算是解题的关键.
(1)根据所给的程序图代入相应的值进行运算即可;
(2)根据所给的程序图代入相应的值进行运算即可.
【详解】解:(1)当时,
,,,,,
故答案为:;
(2)当时,,
解得:;
当,,即:时,
解得:.
故答案为:,(答案不唯一).
题型4 有理数混合运算的实际应用
1.南部县是一座历史文化悠久、人口众多的大县,出租车是重要的交通工具,出租车的计价标准为:行程不超过2千米收费5元,超过2千米的部分按每千米1.5元收费(不足1千米的按1千米计算)一出租车公司坐落于南北方向的南铁大道边,驾驶员张师傅从公司出发,在此大道上连续接送5批客人,行驶记录如下:(注;一批次的客人指的是一次可坐1到4位客人,规定向北为正,向南为负,单位:千米)
第一批 第二批 第三批 第四批 第五批
(1)送完第五批客人后,张师傅在公司的 边(填南或北)距离公司 千米的位置.
(2)张师傅的车平均每千米消耗压缩天然气0.09升,则送完第五批客人后,张师傅用了多少升压缩天然气?
(3)在整个过程中,张师傅共收到车费多少元?
【答案】(1)南,0.4
(2)送完第五批客人后,王师傅用了升压缩天然气
(3)在整个过程中,张师傅共收到车费34元
【分析】本题主要考查了正数和负数的应用,有理数的混合运算,熟练掌握正负数的作用,绝对值的意义,分段计费,是解答本题的关键.
(1)将表格中的数据相加,再根据正负数的意义即可解答;
(2)先计算出在整个过程的总路程,然后乘以每千米消耗压缩天然气0.09升,即可解答;
(3)根据表格中的数据是超过2千米的分段计费,取总和,可以计算出送完第五批客人后,张师傅共收到的车费.
【详解】(1)解:(千米),
即送完第五批客人后,张师傅在公司的南边,距离公司0.4千米的位置;
故答案为:南,0.4;
(2)解:(升,
送完第五批客人后,王师傅用了升压缩天然气;
(3)解:由题可知:
(元,
在整个过程中,张师傅共收到车费34元.
2.科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富,小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负,下表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克)
(1)求小王第一周销售柚子最多的一天比最少的一天多销售多少千克.
(2)求小王第一周实际销售柚子的总量是多少千克?
(3)若小王按8元/千克进行柚子销售,平均运费为2元/千克,则小王第一周销售柚子一共收入多少元?
【答案】(1)小王第一周销售柚子最多的一天比最少的一天多销售千克
(2)小王第一周实际销售柚子的总量是千克
(3)小王第一周销售柚子一共收入元
【分析】本题考查了正负数的实际应用,涉及了有理数的混合运算,注意计算的准确性.
(1)用周六柚子的销量减去周五柚子的销量即可;
(2)计算即可求解;
(3)收入=(售价-运费)×总量,据此即可求解.
【详解】(1)解:周六销售柚子最多,销售量为(千克),
最少的是周五,销售量为(千克),
所以最多的一天比最少的一天多销售(千克)
答:小王第一周销售柚子最多的一天比最少的一天多销售20千克;
(2)解:(千克),
答:小王第一周实际销售柚子的总量是千克;
(3)解:(元),
答:小王第一周销售柚子一共收入元.
3.某仓库原有商品件,现记录了天内该类商品进出仓库的件数如下所示(“”表示进库,“”表示出库):,,,,,,,,,.
(1)请问经过天之后,该仓库内的商品是增加了还是减少了?此时仓库还有多少商品?
(2)如果商品每次进出仓库需要人工搬运费是每件元,请问这天要付多少人工搬运费?
【答案】(1)经过天之后,该仓库内的商品是增加了件,此时仓库还有商品;
(2)这天要付元搬运费.
【分析】本题主要考查了有理数的加法、绝对值,解决本题的关键是根据有理数的加法法则进行计算.
把这天进出仓库的商品件数相加,所得结果为,所以经过天之后,该仓库内的商品增加了件,此时仓库的商品还有件;
【详解】(1)解:(件),
经过天之后,该仓库内的商品件数为:(件),
答:经过天之后,该仓库内的商品是增加了件,此时仓库还有商品;
(2)解:(件),
这天要付给工人的搬运费为:(元),
答:这天要付元搬运费.
4.为巩固脱贫攻坚成果,助力乡村振兴快速发展.我县所略乡推行“发展茶油产业,加快脱贫的步伐”.某种植户新鲜采摘了20筐茶果,以每筐25千克为标准重量,超过或不足千克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:千克) 0 1
筐数 1 4 2 3 2 8
(1)与标准重量比较,20筐茶果总计超过或不足多少千克?
(2)若该种植户采摘生茶果每千克售价元,则出售这20筐茶果可获得多少元?
【答案】(1)20筐茶果的总质量比标准质量超过8千克
(2)出售这20筐茶果可获得元
【分析】本题主要考查了正负数的实际应用,有理数四则混合计算的实际应用,熟知正负数的实际意义是解题的关键.
(1)根据表格中的数据求出这20筐茶果的重量,若结果为正,则超过标准质量,若为负,则不足,若为0,这等于标准质量,据此求解即可;
(2)用每千克的售价乘以茶果总质量即可得到答案.
【详解】(1)解:由题意得:千克,
答:20筐茶果的总质量比标准质量超过8千克;
(2)解:由题意得:(元)
答:出售这20筐茶果可获得元.
5.正值中秋佳节,小梦和妈妈一块去购买月饼,妈妈买了一盒某品牌月饼共计8枚.小梦将8枚月饼的质量称重后统计表如下(单位:克):
第枚 1 2 3 4 5 6 7 8
质量 56 55 54.8 56.2 55.3 55.3 54.7 54.3
(1)小梦为了简化运算,选取了一个恰当的标准质量,依据这个标准质量,小梦把超出的部分记为正,不足的部分记为负,列出表格(不完整).请根据表格计算这个标准质量_______克,下面表格中第3枚月饼的质量是________克;
第枚 1 2 3 4 5 6 7 8
质量 ________ ________ ________ ________ ________
(2)当小梦看到说明书上标记的总质量为克时,小梦妈妈买的月饼在总质量上是否合格?请你通过计算说明为什么.
【答案】(1)55;
(2)合格,理由见详解
【分析】本题考查了正数和负数以及有理数的加减混合运算,正确理解本题中正数和负数的意义是解答本题的关键.
(1)根据题意可知,标准质量为55克,据此可得结果;
(2)求出8次记录的数的和,判断其是否在至之间即可得出答案.
【详解】(1)解:由题意,得标准质量为55克,;
故答案为:55;;
(2)解:由题意得:,
,即,
这盒月饼在总质量上是合格的.
过关练习
一、选择题
1.下面两个量中,不具有相反意义的是( )
A.盈利和亏损元 B.浪费水和节约水
C.进三个球和输三场比赛 D.上升和下降
【答案】C
【分析】此题考查了相反意义的量.根据相反意义的量的定义进行判断即可.
【详解】解:A、盈利和亏损元,是互为相反意义的量,故选项不符合题意;
B、浪费水和节约水,是互为相反意义的量,故选项不符合题意;
C、进三个球和输三场比赛,不是互为相反意义的量,故选项符合题意;
D、上升和下降,是互为相反意义的量,故选项不符合题意;
故选:C.
2.下列四个数中,属于负数的是( )
A.1.2 B.1 C. D.0
【答案】C
【分析】本题考查负数的概念,解题的关键是明确负数的定义,即小于0的数是负数.
明确正数,负数和0的性质,逐一分析选项中的数与0的大小关系.
【详解】A、1.2是正数,A项错误;
B、1是正数,B项错误;
C、小于0,根据负数的定义:小于0的数是负数,所以是负数,C项正确;
D、0既不是正数也不是负数,D项错误.
故选:C.
3.在,,0,1.2,2,中,非负整数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查有理数,理解有理数、非负整数的定义是正确解答的关键.
根据有理数,非负整数的定义进行判断即可.
【详解】解:在,,0,1.2,2,中,非负整数有0,2,共2个,
故选:B.
4.下列各图中,数轴表示正确的是( )
A. B.
C. D.
【答案】D
【分析】本题主要考查数轴的三要素,熟练掌握数轴三要素:原点,单位长度,正方向,即可得到答案.
【详解】解:A、缺少正方形,数轴表示不正确,不符合题意;
B、缺少原点,数轴表示不正确,不符合题意;
C、单位长度不统一,数轴表示不正确,不符合题意;
D、是数轴,符合题意;
故选:D.
5.在数轴上,表示有理数a,b的点的位置如图所示,把个数按照从小到大的顺序排列,正确的是( )
A. B. C. D.
【答案】C
【分析】本题考查数轴的性质以及有理数的大小比较,解题的关键是根据数轴上点的位置判断出a,b的正负性和绝对值大小关系.
先根据数轴判断a,b的正负性与绝对值大小.再根据相反数的性质得到的正负性,最后比较的大小.
【详解】从数轴可知,,且,
根据相反数的性质,的相反数的相反数,
所以,
故选:C.
6.2025的相反数是( )
A. B. C. D.2025
【答案】A
【分析】本题考查了求一个数的相反数,根据只有符号不同的两个数互为相反数进行作答即可.
【详解】解:2025的相反数是,
故选:A.
7.的绝对值是( )
A. B. C. D.2
【答案】A
【分析】本题主要考查了求一个数的绝对值,正数和0的绝对值是它本身,负数的绝对值是它的相反数,据此求解即可.
【详解】解:∵,
∴的绝对值是,
故选:A.
8.算筹我国是最早认识负数并进行相关运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用算筹(小棍形状的记数工具)来表示正负数,其中正放表示正数,斜放表示负数,例如图①表示的是的运算过程.按照这种方法,可推算图②中的算式为( )
A. B.
C. D.
【答案】B
【分析】本题考查了有理数的加法,熟练掌握运算法则是解题的关键.
根据题意列式计算得,即可得到答案.
【详解】解:根据题意得,
故选:B.
9.比低的温度是( )
A. B. C. D.
【答案】D
【分析】本题考查了有理数减法的应用,用减去即可求解.
【详解】解:由题意,得
.
故选D.
10.如果,,那么下列成立的是( )
A., B., C., D.,
【答案】C
【分析】本题主要考查了有理数的加法、除法运算法则,熟知两种运算的法则是正确解答此题的关键.
根据有理数加法法则:①同号相加,取相同符号,并把绝对值相加.②绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.两数相除,同号得正,异号得负,并把绝对值相除,依此即可作出判断.
【详解】解:,
,同为正或同为负,
,
,同为负,即:,;
故选:C.
二、填空题
11.数轴上与点2相距3个单位长度的点表示的数为 .
【答案】或
【分析】本题考查了数轴上两点间的距离,利用分类讨论的思想解决问题是解题关键.
分两种情况讨论:①当点在表示2的点的左边时;②当点在表示2的点的右边时,根据数轴上两点间的距离,即可得到答案.
【详解】解:分为两种情况:
①当点在表示2的点的左边时,与点2相距3个单位长度的点表示的数为;
②当点在表示2的点的右边时,与点2相距3个单位长度的点表示的数为;
故答案为:或.
12.比较大小: (填“”或“”)
【答案】
【分析】本题考查了有理数的大小比较,解题关键是掌握有理数大小比较法则:正数大于零,负数小于零,正数大于一切负数;两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小.
【详解】解:,,,
,
故答案为:.
13.计算: .
【答案】3
【分析】本题考查绝对值的计算,解题的关键是理解绝对值的定义和运算规则.
先计算括号内的运算,再根据绝对值的定义求出结果.
【详解】,
,
故答案为:3.
14. ,
【答案】 /
【分析】本题考查的是化简绝对值及化简多重符号,熟练掌握绝对值性质及化简多重符号的方法是解题关键,根据绝对值及相反数定义直接计算即可.
【详解】解:;
;
;
,
故答案为:,,,.
15.计算:(1) ;
(2) .
【答案】
【分析】本题考查了有理数的加法运算,根据有理数的加法法则求解即可.
【详解】解:(1);
(2);
故答案为:,.
16.若,,,则的绝对值是 .
【答案】
【分析】本题考查了绝对值的定义,有理数加法,首先依据绝对值的定义求得、,结合条件,进行分两种情况计算即可,掌握知识点的应用及分类讨论思想是解题的关键.
【详解】解:∵,,
∴;;
∵,
∴当,时,;
当,时,;
故答案为:.
17.的倒数是 .
【答案】
【分析】本题主要考查了求一个数的倒数,乘积为1的两个数互为倒数,据此求解即可.
【详解】解:∵,
∴的倒数是,
故答案为:.
18.华为最新款手机芯片“麒麟990”是一种微型处理器,每秒可进行次运算,用科学记数法表示为
【答案】
【分析】本题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中为整数,表示时关键要正确确定a的值以及n的值,根据科学记数法的表示方法进行表示即可.
【详解】解:,
故答案为:.
19.定义一种新运算:,则 .
【答案】12
【分析】本题考查了有理数的混合运算,理解定义的新运算是解题的关键.按照定义的新运算进行计算,即可解答.
【详解】解:∵,
∴,
故答案为:12.
20.根据流程图中的程序,若输入x的值为,则输出y的值为 .
【答案】7
【分析】本题考查了有理数的混合运算,代数式求值,掌握有理数的混合运算法则是解题的关键.
先根据流程图的程序列出算式,再计算出结果,根据输出的条件得出结论即可.
【详解】解:把代入,得,
再把代入,得,
∴输出y的值为7.
故答案为:7.
三、解答题
21.计算:
(1);
(2).
【答案】(1)16
(2)
【分析】本题考查了有理数的混合运算:先算乘方,再算乘除,然后进行加减运算;有括号先算括号.
(1)先算乘方和乘除,再算加减即可;
(2)先把除法运算转化为乘法运算,然后利用乘法分配律进行计算.
【详解】(1)解:原式
;
(2)原式
.
22.计算:
(1);
(2).
【答案】(1)23
(2)
【分析】本题主要考查了有理数混合运算,解题的关键是熟练掌握有理数混合运算法则,“先算乘方,再算乘除,最后算加减,有小括号的先算小括号里面的”.
(1)根据乘法分配律进行计算即可;
(2)根据含乘方的有理数混合运算法则进行计算即可.
【详解】(1)解:
;
(2)解:
.
23.探究规律,完成相关题目.
定义“*”运算:
;
;
;
;
;
;
;
;
;
.
归纳*运算的法则(用文字语言叙述)
(1)绝对值不同的两数进行*运算时,结果的绝对值如何确定?_________.
特别地,0和任何数进行*运算,或任何数和0进行*运算,_____.
(2)计算:
(3)是否存在两个非零有理数m,n,使得,若存在,求出m,n满足的关系,若不存在,请说明理由.
【答案】(1)绝对值较大数的平方减去绝对值较小数的平方,得这个数的平方
(2)
(3)存在,或
【分析】本题主要考查含有乘方的有理数的混合运算,绝对值的性质,理解材料中关于“*”运算方法,掌握绝对值的性质,含有乘方的有理数的混合运算法则是解题的关键.
(1)阅读材料,根据材料提示,总结归纳即可求解;
(2)运用材料提示的运算法则进行计算即可;
(3)根据材料提示得到,由此计算即可求解.
【详解】(1)解:由题意得:绝对值不同的两数进行*运算时,结果的绝对值的确定方法是:绝对值较大数的平方减去绝对值较小数的平方,绝对值为正;0和任何数进行*运算,或任何数和0进行*运算,结果都等于这个数的平方;
故答案为:绝对值较大数的平方减去绝对值较小数的平方,绝对值为正;结果都等于这个数的平方;
(2)解:
;
(3)解:存在,理由如下,
∵,
∴,
∴,
∴或,
∴存在两个非零有理数m、n,使得.
24.一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A地出发,晚上最后到达B地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题:
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)
【答案】(1)B地在A地正南方,与A地相距6.6千米.(2)这一天共耗油约为5.4升
【详解】(1)把所给的数值相加,求出结果,若为正,则说明B在A的北边,若为负,则说明B在A的南边;
(2)先求出所有数值绝对值的和,再乘以0.0642即可.
25.最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加,小明家新换了一辆新能源汽车,他连续7天记录了每天行驶的路程(如表).以为标准,多于的记为“+”,不足的记为“-”,刚好的记为“”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程()
(1)这天里路程最多的一天比最少的一天多走______km;(答案直接填写在答题卡的横线上)
(2)请求出小明家的新能源汽车这七天一共行驶了多少千米?
(3)小明家原来的汽油车每行驶需用汽油升,汽油价元/升.现在的新能源汽车每行驶耗电量为度,每度电为元.请估计小明家换成新能源汽车后这天的行驶费用比原来节省多少钱?
【答案】(1)
(2)千米
(3)元
【分析】本题主要考查了有理数的减法应用,解题的关键是掌握有理数的加减运算,有理数的乘除运算,根据有理数的混合运算,进行解答,即可.
(1)根据有理数的减法列式计算即可;
(2)将天的里程求和,即可得解;
(3)用汽油车的费用减去电车的费用,即可得解.
【详解】(1)解:由表格可知,,
∴这 天里路程最多的一天比最少的一天多走.
故答案为:.
(2)解:,
答:小明家的新能源汽车这七天一共行驶了千米.
(3)解:
答:小明家换成新能源汽车后这天的行驶费用比原来节省元.
知识点
知识点1:正数与负数意义
1.具有相反意义的量包括三个要素:具有同类性;具有相反意义;具有数量。
2.正数、负数可以表示两个相反意义的量。
知识点2:有理数及其分类
有理数的概念:有理数是整数和分数的统称。
有理数的四种表现形式:整数、分数、有限小数、无限循环小数。判断一个数是不是有理数,只要看看这个数是不是这四种就行了,如果是这四种中一个,那这个数一定是有理数;如果不是这四种中的任何一种,那它一定不是有理数。
有理数的分类方法:
(1)按概念分类: (2)按正负分类:
知识点3:数轴
1.数轴是规定了原点,正方向,单位长度的直线。
2.数轴的三要素:原点,正方向,单位长度。
知识点4:有理数的大小比较方法
有理数的大小关系:
对于两个有理数,下列三种关系有且仅有一种成立:。
有理数的大小关系的比较方法:方法1:借助数轴比较;方法2:借助绝对值比较。
4.有理数的大小关系具有传递性:
(1)如果,那么就有。(2)如果,那么就有。
知识点5:绝对值与相反数
1.绝对值的定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2.绝对值的表示方法:数a的绝对值记作|a|.
3.绝对值的代数意义:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.即对于任何有理数a都有:
4.绝对值的几何意义:
一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小.
的几何意义:数轴上表示数的点到原点的距离。
5.绝对值的性质:非负性,即任何一个数的绝对值总是正数或0即
6.相反数的定义:只有符号不同的两个数互为相反数;0的相反数是0.
7.相反数的表示方法:的相反数为。
8.相反数的性质:
(1)位置关系:互为相反数的两数的点分别位于原点的两旁,且与原点的距离相等.
(2)和的关系:互为相反数的两数和为0.
知识点6:有理数的加法法则
1.加法法则
加数类型 加法法则 典型范例
同号两数相加 同号两数相加,取相同的符号,并把绝对值相加;
异号两数相加 异号两数相加,绝对值相等时,和为0
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值
一数与0相加 一个数同0相加,仍得这个数
知识点7:有理数的加法运算律
1.加法运算律:
(1)加法交换律:
(2)加法结合律:
名师点拨:
(1)加法运算律的作用:简化运算,凑整,凑同号;
(2)交换加数的位置时,不要忘记符号.
知识点8:有理数的减法法则
有理数减法法则:减去一个数,等于加这个数的相反数,即有:.
名师点拨:
(1)将减法转化为加法时,注意“两变”,一变是减号变加号;二变是把减数变为它的相反数”.
(2)灵活使用减法法则,比较熟练的同学也可以不按步骤,直接写结果,提高效率。
知识点9:有理数的乘法法则
有理数的乘法法则:
(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
名师点拨:
(1)不为0的两数相乘,先定符号,再把绝对值相乘.
(2)当乘数中有负数时,必须用括号括起来:
如5与-3的乘积,应列为5×(-3),不应该写成5×-3.
2.有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积相等,
即:.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
即:.
(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
即:.
知识点10:有理数的除法法则
1.有理数除法法则:
(1)法则1:除以一个不等于0的数,等于乘这个数的倒数,即。
(2)法则2:两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
2. 倒数的概念: 乘积是1的两个数互为倒数.
名师点拨:
(1)0不能当除数;
(2)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.
知识点11:有理数的乘方
1.乘方的概念:求相同因数的积的运算,叫做乘方,乘方的结果叫做幂(power).
即有:.
底数:在中,叫做底数,
指数:叫做指数.
典型例子:此处2叫做底数,3是指数,表示2的个数;
2.特例:当指数=2时,一般成为平方;当指数=3时,一般成为立方。
知识点12:科学记数法(这是一个很小,但非常非常重要的知识点,要牢记)
科学记数法的定义:
把一个绝对值大于10的数表示成的形式(其中l≤||<10,是正整数),这种记数法叫做科学记数法.
名师点拨:
(1)负数也可以用科学记数法表示,“”照写,其它与正数一样;
(2)把一个数写成形式时,若这个数是大于10的数,则n比这个数的整数位数少1.
知识点13:有理数的混合运算
1.有理数的混合运算顺序:(混合运算三原则)
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2.合理运用运算律简化运算
1.加法运算律:
加法交换律:
加法结合律:
2.乘法交换律:
乘法交换律:
乘法结合律:
乘法分配律:
3.灵活选用适当的运算律,可以简化计算,减少错误。运用乘法分配率时要根据自己的基础情况选用。
典型例题
教材习题第66页复习题第7(3)题 计算: 解题方法指导 解法1:直接通分计算 解法2:可以使用分配率计算
【分析】 解法1:直接通分计算 解法1:直接通分计算
教材习题69页复习题探索研究第18题 如果的绝对值和相等,那么满足什么条件? 如果的绝对值比大,那么满足什么条件? 解题方法指导 举出各种类型的数,比如负数,0,正数,通过对特例的研究,发现其中的规律; 从特殊到一般是我们研究一些较难问题的一般方法
【分析】 先举出一些特殊的各种类型的数,进行研究判断: 第(1)题:为正数时,发现 为负数时,发现,不符合题意 时,,发现 总结:当为非负数时,。 第(2)题:可以采用类似的方法解决: 根据上题可以知道,为正数时 ,不符合题意; 为负数时,发现,符合题意 时,,发现,不符合题意 总结:当为负数时,。
题型训练
题型1 有理数的混合运算问题
1.计算:
(1); (2);
(3); (4).
2.计算:
(1) (2)
(3) (4)
3.计算:
(1) (2)
(3) (4)
4.计算.
(1); (2);
(3); (4).
5.解决下列问题:
(1); (2);
(3); (4).
题型2 有理数简便运算
简便运算:
简便计算:.
简便计算:;
4.用简便方法计算:
(1) ; (2) .
5.简便计算:
(1) (2)
题型3 有理数混合运算的新定义问题
1.对于任意有理数a,b,我们定义一种新运算“”,规定:,如:.
(1)求的值;
(2)求的值.
2.我们定义一种新运算:.例如:.
(1)求的值;
(2)求的值.
3.若定义一种新的运算“”,规定有理数,如.
(1)求的值;
(2)求的值.
4.定义新运算:当时,;当时,;当其中,是实数,如.计算:
(1);
(2).
5.定义一种新的运算:,如:,
求:
(1);
(2).
题型4 与有理数混合运算有关的程序图问题
1.嘉琪同学在自学了简单的电脑编程后,设计了如图所示的程序.
(1)若开始输入为,请你根据程序列出算式并计算出输出结果;
(2)嘉琪发现将一个小于的数输入,得到的结果总是正数.请验证这个结论.
2.小鹏做了一个如图所示的程序图,按要求完成下列各小题.
(1)当小鹏输入的数为6时,求输出的结果n;
(2)若小鹏某次输入数m后,输出的结果n为.请你写出m可能的2个值.
3.有三种运算程序如下图所示,按要求完成下列各题:
(1)如图,当输入数时,输出数_____;
(2)如图,第一个带?号的运算框内,应填_____;第二个带?号的运算框内,应填_____;第三个带?号的运算框内,应填_____.
(3)如图,当输入时,则输出结果为_____.
4.按照如图和图所示的程序,进行计算.
(1)如果输入,求输出结果;
(2)若在图基础上增加一个计算程序“”,如图,重新输入,第一次运算得到,求输出结果.
5.如图所示、淇淇做了一个程序图,按要求完成下列问题.
(1)当淇淇输入的数为6时,则输出的结果
(2)若淇淇某次输入数m后,输出的结果n为,请你写出m的两个可能值
题型5 有理数混合运算的实际应用
1.南部县是一座历史文化悠久、人口众多的大县,出租车是重要的交通工具,出租车的计价标准为:行程不超过2千米收费5元,超过2千米的部分按每千米1.5元收费(不足1千米的按1千米计算)一出租车公司坐落于南北方向的南铁大道边,驾驶员张师傅从公司出发,在此大道上连续接送5批客人,行驶记录如下:(注;一批次的客人指的是一次可坐1到4位客人,规定向北为正,向南为负,单位:千米)
第一批 第二批 第三批 第四批 第五批
(1)送完第五批客人后,张师傅在公司的 边(填南或北)距离公司 千米的位置.
(2)张师傅的车平均每千米消耗压缩天然气0.09升,则送完第五批客人后,张师傅用了多少升压缩天然气?
(3)在整个过程中,张师傅共收到车费多少元?
2.科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富,小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负,下表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克)
(1)求小王第一周销售柚子最多的一天比最少的一天多销售多少千克.
(2)求小王第一周实际销售柚子的总量是多少千克?
(3)若小王按8元/千克进行柚子销售,平均运费为2元/千克,则小王第一周销售柚子一共收入多少元?
3.某仓库原有商品件,现记录了天内该类商品进出仓库的件数如下所示(“”表示进库,“”表示出库):,,,,,,,,,.
(1)请问经过天之后,该仓库内的商品是增加了还是减少了?此时仓库还有多少商品?
(2)如果商品每次进出仓库需要人工搬运费是每件元,请问这天要付多少人工搬运费?
4.为巩固脱贫攻坚成果,助力乡村振兴快速发展.我县所略乡推行“发展茶油产业,加快脱贫的步伐”.某种植户新鲜采摘了20筐茶果,以每筐25千克为标准重量,超过或不足千克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:千克) 0 1
筐数 1 4 2 3 2 8
(1)与标准重量比较,20筐茶果总计超过或不足多少千克?
(2)若该种植户采摘生茶果每千克售价元,则出售这20筐茶果可获得多少元?
5.正值中秋佳节,小梦和妈妈一块去购买月饼,妈妈买了一盒某品牌月饼共计8枚.小梦将8枚月饼的质量称重后统计表如下(单位:克):
第枚 1 2 3 4 5 6 7 8
质量 56 55 54.8 56.2 55.3 55.3 54.7 54.3
(1)小梦为了简化运算,选取了一个恰当的标准质量,依据这个标准质量,小梦把超出的部分记为正,不足的部分记为负,列出表格(不完整).请根据表格计算这个标准质量_______克,下面表格中第3枚月饼的质量是________克;
第枚 1 2 3 4 5 6 7 8
质量 ________ ________ ________ ________ ________
当小梦看到说明书上标记的总质量为克时,小梦妈妈买的月饼在总质量上是否合格?请你通过计算说明为什么.
过关训练
一、选择题
1.下面两个量中,不具有相反意义的是( )
A.盈利和亏损元 B.浪费水和节约水
C.进三个球和输三场比赛 D.上升和下降
2.下列四个数中,属于负数的是( )
A.1.2 B.1 C. D.0
3.在,,0,1.2,2,中,非负整数有( )
A.1个 B.2个 C.3个 D.4个
4.下列各图中,数轴表示正确的是( )
A. B.
C. D.
5.在数轴上,表示有理数a,b的点的位置如图所示,把个数按照从小到大的顺序排列,正确的是( )
A. B. C. D.
6.2025的相反数是( )
A. B. C. D.2025
7.的绝对值是( )
A. B. C. D.2
8.算筹我国是最早认识负数并进行相关运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用算筹(小棍形状的记数工具)来表示正负数,其中正放表示正数,斜放表示负数,例如图①表示的是的运算过程.按照这种方法,可推算图②中的算式为( )
A. B.
C. D.
9.比低的温度是( )
A. B. C. D.
10.如果,,那么下列成立的是( )
A., B., C., D.,
二、填空题
11.数轴上与点2相距3个单位长度的点表示的数为 .
12.比较大小: (填“”或“”)
13.计算: .
14. ,
15.计算:(1) ;
(2) .
16.若,,,则的绝对值是 .
17.的倒数是 .
18.华为最新款手机芯片“麒麟990”是一种微型处理器,每秒可进行次运算,用科学记数法表示为
19.定义一种新运算:,则 .
20.根据流程图中的程序,若输入x的值为,则输出y的值为 .
三、解答题
21.计算:
(1);
(2).
22.计算:
(1);
(2).
23.探究规律,完成相关题目.
定义“*”运算:
;
;
;
;
;
;
;
;
;
.
归纳*运算的法则(用文字语言叙述)
(1)绝对值不同的两数进行*运算时,结果的绝对值如何确定?_________.
特别地,0和任何数进行*运算,或任何数和0进行*运算,_____.
(2)计算:
(3)是否存在两个非零有理数m,n,使得,若存在,求出m,n满足的关系,若不存在,请说明理由.
24.一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A地出发,晚上最后到达B地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题:
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)
25.最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加,小明家新换了一辆新能源汽车,他连续7天记录了每天行驶的路程(如表).以为标准,多于的记为“+”,不足的记为“-”,刚好的记为“”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程()
(1)这天里路程最多的一天比最少的一天多走______km;(答案直接填写在答题卡的横线上)
(2)请求出小明家的新能源汽车这七天一共行驶了多少千米?
(3)小明家原来的汽油车每行驶需用汽油升,汽油价元/升.现在的新能源汽车每行驶耗电量为度,每度电为元.请估计小明家换成新能源汽车后这天的行驶费用比原来节省多少钱?
答案解析
题型练习
题型1 有理数的混合运算问题
1.计算:
(1); (2);
(3); (4).
【答案】(1)1
(2)
(3)
(4)
【分析】本题考查有理数的含有乘方的混合运算.解题关键是熟练掌握运算法则是解题的关键.
(1)有理数的加减运算法则计算即可;
(2)根据乘法分配律计算即可;
(3)将除法转化为乘法,根据乘法计算即可;
(4)先算乘方和绝对值,再算乘除法,再算加法
【详解】(1)解:
;
(2)解:
+
;
(3)解:
;
(4)解:
;
2.计算:
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查的是求一个数的绝对值,加法的运算律,乘法的运算律,含乘方的有理数的混合运算,掌握有理数加减乘除,乘方运算的运算法则与运算顺序是解题的关键.
(1)利用加法的运算律,把分母相同的两个数先加,从而可得答案;
(2)利用乘法的分配律把原式化为:,再计算乘法,最后计算加减运算即可;
(3)先计算括号内的运算,同步计算乘方运算,再计算乘法运算,最后计算加减运算即可;
(4)先计算乘方运算,同步计算除法与绝对值,再计算乘法运算,最后计算加减运算即可.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
3.计算:
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查了有理数的混合运算;
(1)利用加法交换律和结合律进行计算,即可解答;
(2)利用乘法分配律进行计算,即可解答;
(3)先算乘方,再算乘除,后算加减,即可解答;
(4)先算乘方,再算乘法,后算加减,有括号先算括号里,即可解答.
【详解】(1)解:
;
(2)解:
;
(3)解:
(4)解:
4.计算.
(1);
(2);
(3);
(4).
【答案】(1)
(2)
(3)2
(4)15
【分析】本题考查了有理数的四则混合运算和含乘方的有理数的混合运算,熟练掌握运算法则和顺序是解题的关键.
(1)先计算绝对值和有理数的乘除,再计算有理数的加减,即得答案;
(2)先计算有理数的乘方,然后计算两个括号中的加减,再计算有理数的乘法,最后计算有理数的加减,即得答案.
(3)先算括号,再算除法即可;
(4)先算乘方,再算乘除,最后算加减即可.
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
5.解决下列问题:
(1);
(2);
(3);
(4).
【答案】(1)3
(2)
(3)3
(4)
【分析】本题考查了有理数的混合运算,熟练掌握运算法则是解答本题的关键.
(1)把减法统一成加法,再按加法法则计算;
(2)利用乘法分配律计算即可;
(3)先算乘方,再算除法,后算加减;
(4)先算乘方、除法、绝对值,再算乘法,后算加减
【详解】(1)解:
(2)解:
(3)解:
(4)解:
题型2 有理数简便运算
简便运算:
【答案】
【分析】本题主要考查了含乘方的有理数混合计算,有理数乘法分配律,先把原式变形为,再利用乘法结合律变形得到,据此利用乘法分配律求解即可.
【详解】解:
.
简便计算:.
【答案】25
【分析】本题主要考查了含乘方的有理数混合运算、有理数乘法运算律的简便运算等知识点,掌握相关运算法则和运算律成为解题的关键.
运用有理数的乘法运算律进行简便运算即可.
【详解】解:
.
简便计算:;
【答案】
【分析】先确定积的符号,再逆用乘法分配律进行简便运算即可;
【详解】解:
;
4.用简便方法计算:
(1) ; (2) .
【答案】(1)
(2)
【分析】(1)把改写成,把改写成,然后把除法转化为乘法,再按乘法分配律计算即可;
(2)先算乘方,然后把一、四项结合,二、三项结合,逆用乘法分配律计算.
【详解】(1)解:原式
.
(2)解:原式
.
5.简便计算:
(1) (2)
【答案】(1);(2)
【分析】(1)根据逆用乘法分配率进行计算即可;
(2)先计算括号内的,再根据乘法分配律简便运算即可.
【详解】(1)
(2)
题型3 有理数混合运算的新定义问题
1.对于任意有理数a,b,我们定义一种新运算“”,规定:,如:.
(1)求的值;
(2)求的值.
【答案】(1)49;
(2)109.
【分析】本题主要考查了有理数的混合运算,理解新定义是解题的关键.
(1)直接根据新定义的法则,结合有理数的相应的运算法则进行运算即可.
(2)先根据新定义计算,再计算即可求解.
【详解】(1)解:
.
所以的值为49.
(2)解:
;
.
所以的值为109.
2.我们定义一种新运算:.例如:.
(1)求的值;
(2)求的值.
【答案】(1)1
(2)4
【分析】本题主要考查了新定义,含乘方的有理数混合计算:
(1)根据新定义得到,据此代值计算即可;
(2)根据新定义得到,再根据,进行计算求解即可.
【详解】(1)解:由题意得:
;
(2)解:
.
3.若定义一种新的运算“”,规定有理数,如.
(1)求的值;
(2)求的值.
【答案】(1)21
(2)40
【分析】本题考查了新定义和有理数的混合运算,正确理解新定义和有理数的运算法则解题的关键.
(1)按照新定义法则把原式转化为有理数运算,再计算即可;
(2)按照新定义法则把原式转化为有理数运算,再计算即可.
【详解】(1)解:;
(2)解:,
∴.
4.定义新运算:当时,;当时,;当其中,是实数,如.计算:
(1);
(2).
【答案】(1)
(2).
【分析】()根据新定义列出算式,然后根据运算法则即可求解;
()根据新定义列出算式,然后根据运算法则即可求解;
本题考查了有理数的混合运算,熟练掌握运算法则是解题的关键.
【详解】(1)
解:
;
(2)
解:
,
则
.
5.定义一种新的运算:,如:,
求:
(1);
(2).
【答案】(1)
(2)
【分析】此题考查了新定义运算和有理数的混合运算,弄清题中的新定义是解本题的关键.
(1)把原式利用题中的新定义计算转换为有理数运算,即可得到结果;
(2)先计算,求得,再计算,即可得到结果.
【详解】(1)解:由题意得:
;
(2)解:由题意得:
.
题型4 与有理数混合运算有关的程序图问题
1.嘉琪同学在自学了简单的电脑编程后,设计了如图所示的程序.
(1)若开始输入为,请你根据程序列出算式并计算出输出结果;
(2)嘉琪发现将一个小于的数输入,得到的结果总是正数.请验证这个结论.
【答案】(1);
(2)见解析
【分析】本题主要考查了有理数的混合运算,不等式的性质,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(1)首先用开始输入的数乘,求出积是多少;然后用所得的积除以2,求出商是多少;最后用所得的商减去即可.
(2)这个数是x,得出程序的结果为,再令,代入验证即可.
【详解】(1)解:
;
(2)解:设这个数是x,则,
,
,
,即得到的结果总是正数.
2.小鹏做了一个如图所示的程序图,按要求完成下列各小题.
(1)当小鹏输入的数为6时,求输出的结果n;
(2)若小鹏某次输入数m后,输出的结果n为.请你写出m可能的2个值.
【答案】(1)
(2)或0.5
【分析】本题考查程序流程图与有理数运算:
(1)根据流程图,列出算式进行计算即可;
(2)分或两种情况进行讨论求解即可.
【详解】(1)解:当时,,
,
,
,
;
(2),
当时,,
当时,;
故m可能为或0.5.
3.有三种运算程序如下图所示,按要求完成下列各题:
(1)如图,当输入数时,输出数_____;
(2)如图,第一个带?号的运算框内,应填_____;第二个带?号的运算框内,应填_____;第三个带?号的运算框内,应填_____.
(3)如图,当输入时,则输出结果为_____.
【答案】(1)
(2),,
(3)
【分析】(1)利用图中公式计算得出答案;
(2)利用最后的代数式推出空格中的式子;
(3)根据图中计算公式及判断条件分别计算得出答案.
【详解】(1)解:如图,当输入数时,输出数,
故答案为:;
(2)解:第一个带?号的运算框内,应填:,
第二个带?号的运算框内,应填:,
第三个带?号的运算框内,应填:,
故答案为:,,;
(3)解:,
,
,
,
,
,
,
,
,
输出结果为:,
故答案为:.
【点睛】本题主要考查了程序流程图与有理数计算,有理数四则混合运算,代数式表示的实际意义,程序流程图与代数式求值等知识点,看懂程序流程图并得出正确信息是解题的关键.
4.按照如图和图所示的程序,进行计算.
(1)如果输入,求输出结果;
(2)若在图基础上增加一个计算程序“”,如图,重新输入,第一次运算得到,求输出结果.
【答案】(1);
(2).
【分析】本题主要考查了流程图,有理数的混合运算,解分式方程等知识点,根据流程图正确列式是解题的关键.
()根据程序中的运算法则列式计算即可;
()根据程序中的运算法则列出分式方程,求出的值,再根据运算法则列式计算即可.
【详解】(1)解:
;
(2)解:,
,
∴,
经检验,是原分式方程的解,
∴
.
5.如图所示、淇淇做了一个程序图,按要求完成下列问题.
(1)当淇淇输入的数为6时,则输出的结果
(2)若淇淇某次输入数m后,输出的结果n为,请你写出m的两个可能值
【答案】 ,(答案不唯一)
【分析】本题考查程序流程图和有理数的运算,按照程序流程图准确的进行计算是解题的关键.
(1)根据所给的程序图代入相应的值进行运算即可;
(2)根据所给的程序图代入相应的值进行运算即可.
【详解】解:(1)当时,
,,,,,
故答案为:;
(2)当时,,
解得:;
当,,即:时,
解得:.
故答案为:,(答案不唯一).
题型4 有理数混合运算的实际应用
1.南部县是一座历史文化悠久、人口众多的大县,出租车是重要的交通工具,出租车的计价标准为:行程不超过2千米收费5元,超过2千米的部分按每千米1.5元收费(不足1千米的按1千米计算)一出租车公司坐落于南北方向的南铁大道边,驾驶员张师傅从公司出发,在此大道上连续接送5批客人,行驶记录如下:(注;一批次的客人指的是一次可坐1到4位客人,规定向北为正,向南为负,单位:千米)
第一批 第二批 第三批 第四批 第五批
(1)送完第五批客人后,张师傅在公司的 边(填南或北)距离公司 千米的位置.
(2)张师傅的车平均每千米消耗压缩天然气0.09升,则送完第五批客人后,张师傅用了多少升压缩天然气?
(3)在整个过程中,张师傅共收到车费多少元?
【答案】(1)南,0.4
(2)送完第五批客人后,王师傅用了升压缩天然气
(3)在整个过程中,张师傅共收到车费34元
【分析】本题主要考查了正数和负数的应用,有理数的混合运算,熟练掌握正负数的作用,绝对值的意义,分段计费,是解答本题的关键.
(1)将表格中的数据相加,再根据正负数的意义即可解答;
(2)先计算出在整个过程的总路程,然后乘以每千米消耗压缩天然气0.09升,即可解答;
(3)根据表格中的数据是超过2千米的分段计费,取总和,可以计算出送完第五批客人后,张师傅共收到的车费.
【详解】(1)解:(千米),
即送完第五批客人后,张师傅在公司的南边,距离公司0.4千米的位置;
故答案为:南,0.4;
(2)解:(升,
送完第五批客人后,王师傅用了升压缩天然气;
(3)解:由题可知:
(元,
在整个过程中,张师傅共收到车费34元.
2.科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富,小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负,下表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克)
(1)求小王第一周销售柚子最多的一天比最少的一天多销售多少千克.
(2)求小王第一周实际销售柚子的总量是多少千克?
(3)若小王按8元/千克进行柚子销售,平均运费为2元/千克,则小王第一周销售柚子一共收入多少元?
【答案】(1)小王第一周销售柚子最多的一天比最少的一天多销售千克
(2)小王第一周实际销售柚子的总量是千克
(3)小王第一周销售柚子一共收入元
【分析】本题考查了正负数的实际应用,涉及了有理数的混合运算,注意计算的准确性.
(1)用周六柚子的销量减去周五柚子的销量即可;
(2)计算即可求解;
(3)收入=(售价-运费)×总量,据此即可求解.
【详解】(1)解:周六销售柚子最多,销售量为(千克),
最少的是周五,销售量为(千克),
所以最多的一天比最少的一天多销售(千克)
答:小王第一周销售柚子最多的一天比最少的一天多销售20千克;
(2)解:(千克),
答:小王第一周实际销售柚子的总量是千克;
(3)解:(元),
答:小王第一周销售柚子一共收入元.
3.某仓库原有商品件,现记录了天内该类商品进出仓库的件数如下所示(“”表示进库,“”表示出库):,,,,,,,,,.
(1)请问经过天之后,该仓库内的商品是增加了还是减少了?此时仓库还有多少商品?
(2)如果商品每次进出仓库需要人工搬运费是每件元,请问这天要付多少人工搬运费?
【答案】(1)经过天之后,该仓库内的商品是增加了件,此时仓库还有商品;
(2)这天要付元搬运费.
【分析】本题主要考查了有理数的加法、绝对值,解决本题的关键是根据有理数的加法法则进行计算.
把这天进出仓库的商品件数相加,所得结果为,所以经过天之后,该仓库内的商品增加了件,此时仓库的商品还有件;
【详解】(1)解:(件),
经过天之后,该仓库内的商品件数为:(件),
答:经过天之后,该仓库内的商品是增加了件,此时仓库还有商品;
(2)解:(件),
这天要付给工人的搬运费为:(元),
答:这天要付元搬运费.
4.为巩固脱贫攻坚成果,助力乡村振兴快速发展.我县所略乡推行“发展茶油产业,加快脱贫的步伐”.某种植户新鲜采摘了20筐茶果,以每筐25千克为标准重量,超过或不足千克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:千克) 0 1
筐数 1 4 2 3 2 8
(1)与标准重量比较,20筐茶果总计超过或不足多少千克?
(2)若该种植户采摘生茶果每千克售价元,则出售这20筐茶果可获得多少元?
【答案】(1)20筐茶果的总质量比标准质量超过8千克
(2)出售这20筐茶果可获得元
【分析】本题主要考查了正负数的实际应用,有理数四则混合计算的实际应用,熟知正负数的实际意义是解题的关键.
(1)根据表格中的数据求出这20筐茶果的重量,若结果为正,则超过标准质量,若为负,则不足,若为0,这等于标准质量,据此求解即可;
(2)用每千克的售价乘以茶果总质量即可得到答案.
【详解】(1)解:由题意得:千克,
答:20筐茶果的总质量比标准质量超过8千克;
(2)解:由题意得:(元)
答:出售这20筐茶果可获得元.
5.正值中秋佳节,小梦和妈妈一块去购买月饼,妈妈买了一盒某品牌月饼共计8枚.小梦将8枚月饼的质量称重后统计表如下(单位:克):
第枚 1 2 3 4 5 6 7 8
质量 56 55 54.8 56.2 55.3 55.3 54.7 54.3
(1)小梦为了简化运算,选取了一个恰当的标准质量,依据这个标准质量,小梦把超出的部分记为正,不足的部分记为负,列出表格(不完整).请根据表格计算这个标准质量_______克,下面表格中第3枚月饼的质量是________克;
第枚 1 2 3 4 5 6 7 8
质量 ________ ________ ________ ________ ________
(2)当小梦看到说明书上标记的总质量为克时,小梦妈妈买的月饼在总质量上是否合格?请你通过计算说明为什么.
【答案】(1)55;
(2)合格,理由见详解
【分析】本题考查了正数和负数以及有理数的加减混合运算,正确理解本题中正数和负数的意义是解答本题的关键.
(1)根据题意可知,标准质量为55克,据此可得结果;
(2)求出8次记录的数的和,判断其是否在至之间即可得出答案.
【详解】(1)解:由题意,得标准质量为55克,;
故答案为:55;;
(2)解:由题意得:,
,即,
这盒月饼在总质量上是合格的.
过关练习
一、选择题
1.下面两个量中,不具有相反意义的是( )
A.盈利和亏损元 B.浪费水和节约水
C.进三个球和输三场比赛 D.上升和下降
【答案】C
【分析】此题考查了相反意义的量.根据相反意义的量的定义进行判断即可.
【详解】解:A、盈利和亏损元,是互为相反意义的量,故选项不符合题意;
B、浪费水和节约水,是互为相反意义的量,故选项不符合题意;
C、进三个球和输三场比赛,不是互为相反意义的量,故选项符合题意;
D、上升和下降,是互为相反意义的量,故选项不符合题意;
故选:C.
2.下列四个数中,属于负数的是( )
A.1.2 B.1 C. D.0
【答案】C
【分析】本题考查负数的概念,解题的关键是明确负数的定义,即小于0的数是负数.
明确正数,负数和0的性质,逐一分析选项中的数与0的大小关系.
【详解】A、1.2是正数,A项错误;
B、1是正数,B项错误;
C、小于0,根据负数的定义:小于0的数是负数,所以是负数,C项正确;
D、0既不是正数也不是负数,D项错误.
故选:C.
3.在,,0,1.2,2,中,非负整数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查有理数,理解有理数、非负整数的定义是正确解答的关键.
根据有理数,非负整数的定义进行判断即可.
【详解】解:在,,0,1.2,2,中,非负整数有0,2,共2个,
故选:B.
4.下列各图中,数轴表示正确的是( )
A. B.
C. D.
【答案】D
【分析】本题主要考查数轴的三要素,熟练掌握数轴三要素:原点,单位长度,正方向,即可得到答案.
【详解】解:A、缺少正方形,数轴表示不正确,不符合题意;
B、缺少原点,数轴表示不正确,不符合题意;
C、单位长度不统一,数轴表示不正确,不符合题意;
D、是数轴,符合题意;
故选:D.
5.在数轴上,表示有理数a,b的点的位置如图所示,把个数按照从小到大的顺序排列,正确的是( )
A. B. C. D.
【答案】C
【分析】本题考查数轴的性质以及有理数的大小比较,解题的关键是根据数轴上点的位置判断出a,b的正负性和绝对值大小关系.
先根据数轴判断a,b的正负性与绝对值大小.再根据相反数的性质得到的正负性,最后比较的大小.
【详解】从数轴可知,,且,
根据相反数的性质,的相反数的相反数,
所以,
故选:C.
6.2025的相反数是( )
A. B. C. D.2025
【答案】A
【分析】本题考查了求一个数的相反数,根据只有符号不同的两个数互为相反数进行作答即可.
【详解】解:2025的相反数是,
故选:A.
7.的绝对值是( )
A. B. C. D.2
【答案】A
【分析】本题主要考查了求一个数的绝对值,正数和0的绝对值是它本身,负数的绝对值是它的相反数,据此求解即可.
【详解】解:∵,
∴的绝对值是,
故选:A.
8.算筹我国是最早认识负数并进行相关运算的国家,魏晋时期的数学家刘徽在其著作《九章算术注》中,用算筹(小棍形状的记数工具)来表示正负数,其中正放表示正数,斜放表示负数,例如图①表示的是的运算过程.按照这种方法,可推算图②中的算式为( )
A. B.
C. D.
【答案】B
【分析】本题考查了有理数的加法,熟练掌握运算法则是解题的关键.
根据题意列式计算得,即可得到答案.
【详解】解:根据题意得,
故选:B.
9.比低的温度是( )
A. B. C. D.
【答案】D
【分析】本题考查了有理数减法的应用,用减去即可求解.
【详解】解:由题意,得
.
故选D.
10.如果,,那么下列成立的是( )
A., B., C., D.,
【答案】C
【分析】本题主要考查了有理数的加法、除法运算法则,熟知两种运算的法则是正确解答此题的关键.
根据有理数加法法则:①同号相加,取相同符号,并把绝对值相加.②绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.两数相除,同号得正,异号得负,并把绝对值相除,依此即可作出判断.
【详解】解:,
,同为正或同为负,
,
,同为负,即:,;
故选:C.
二、填空题
11.数轴上与点2相距3个单位长度的点表示的数为 .
【答案】或
【分析】本题考查了数轴上两点间的距离,利用分类讨论的思想解决问题是解题关键.
分两种情况讨论:①当点在表示2的点的左边时;②当点在表示2的点的右边时,根据数轴上两点间的距离,即可得到答案.
【详解】解:分为两种情况:
①当点在表示2的点的左边时,与点2相距3个单位长度的点表示的数为;
②当点在表示2的点的右边时,与点2相距3个单位长度的点表示的数为;
故答案为:或.
12.比较大小: (填“”或“”)
【答案】
【分析】本题考查了有理数的大小比较,解题关键是掌握有理数大小比较法则:正数大于零,负数小于零,正数大于一切负数;两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小.
【详解】解:,,,
,
故答案为:.
13.计算: .
【答案】3
【分析】本题考查绝对值的计算,解题的关键是理解绝对值的定义和运算规则.
先计算括号内的运算,再根据绝对值的定义求出结果.
【详解】,
,
故答案为:3.
14. ,
【答案】 /
【分析】本题考查的是化简绝对值及化简多重符号,熟练掌握绝对值性质及化简多重符号的方法是解题关键,根据绝对值及相反数定义直接计算即可.
【详解】解:;
;
;
,
故答案为:,,,.
15.计算:(1) ;
(2) .
【答案】
【分析】本题考查了有理数的加法运算,根据有理数的加法法则求解即可.
【详解】解:(1);
(2);
故答案为:,.
16.若,,,则的绝对值是 .
【答案】
【分析】本题考查了绝对值的定义,有理数加法,首先依据绝对值的定义求得、,结合条件,进行分两种情况计算即可,掌握知识点的应用及分类讨论思想是解题的关键.
【详解】解:∵,,
∴;;
∵,
∴当,时,;
当,时,;
故答案为:.
17.的倒数是 .
【答案】
【分析】本题主要考查了求一个数的倒数,乘积为1的两个数互为倒数,据此求解即可.
【详解】解:∵,
∴的倒数是,
故答案为:.
18.华为最新款手机芯片“麒麟990”是一种微型处理器,每秒可进行次运算,用科学记数法表示为
【答案】
【分析】本题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中为整数,表示时关键要正确确定a的值以及n的值,根据科学记数法的表示方法进行表示即可.
【详解】解:,
故答案为:.
19.定义一种新运算:,则 .
【答案】12
【分析】本题考查了有理数的混合运算,理解定义的新运算是解题的关键.按照定义的新运算进行计算,即可解答.
【详解】解:∵,
∴,
故答案为:12.
20.根据流程图中的程序,若输入x的值为,则输出y的值为 .
【答案】7
【分析】本题考查了有理数的混合运算,代数式求值,掌握有理数的混合运算法则是解题的关键.
先根据流程图的程序列出算式,再计算出结果,根据输出的条件得出结论即可.
【详解】解:把代入,得,
再把代入,得,
∴输出y的值为7.
故答案为:7.
三、解答题
21.计算:
(1);
(2).
【答案】(1)16
(2)
【分析】本题考查了有理数的混合运算:先算乘方,再算乘除,然后进行加减运算;有括号先算括号.
(1)先算乘方和乘除,再算加减即可;
(2)先把除法运算转化为乘法运算,然后利用乘法分配律进行计算.
【详解】(1)解:原式
;
(2)原式
.
22.计算:
(1);
(2).
【答案】(1)23
(2)
【分析】本题主要考查了有理数混合运算,解题的关键是熟练掌握有理数混合运算法则,“先算乘方,再算乘除,最后算加减,有小括号的先算小括号里面的”.
(1)根据乘法分配律进行计算即可;
(2)根据含乘方的有理数混合运算法则进行计算即可.
【详解】(1)解:
;
(2)解:
.
23.探究规律,完成相关题目.
定义“*”运算:
;
;
;
;
;
;
;
;
;
.
归纳*运算的法则(用文字语言叙述)
(1)绝对值不同的两数进行*运算时,结果的绝对值如何确定?_________.
特别地,0和任何数进行*运算,或任何数和0进行*运算,_____.
(2)计算:
(3)是否存在两个非零有理数m,n,使得,若存在,求出m,n满足的关系,若不存在,请说明理由.
【答案】(1)绝对值较大数的平方减去绝对值较小数的平方,得这个数的平方
(2)
(3)存在,或
【分析】本题主要考查含有乘方的有理数的混合运算,绝对值的性质,理解材料中关于“*”运算方法,掌握绝对值的性质,含有乘方的有理数的混合运算法则是解题的关键.
(1)阅读材料,根据材料提示,总结归纳即可求解;
(2)运用材料提示的运算法则进行计算即可;
(3)根据材料提示得到,由此计算即可求解.
【详解】(1)解:由题意得:绝对值不同的两数进行*运算时,结果的绝对值的确定方法是:绝对值较大数的平方减去绝对值较小数的平方,绝对值为正;0和任何数进行*运算,或任何数和0进行*运算,结果都等于这个数的平方;
故答案为:绝对值较大数的平方减去绝对值较小数的平方,绝对值为正;结果都等于这个数的平方;
(2)解:
;
(3)解:存在,理由如下,
∵,
∴,
∴,
∴或,
∴存在两个非零有理数m、n,使得.
24.一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A地出发,晚上最后到达B地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题:
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)
【答案】(1)B地在A地正南方,与A地相距6.6千米.(2)这一天共耗油约为5.4升
【详解】(1)把所给的数值相加,求出结果,若为正,则说明B在A的北边,若为负,则说明B在A的南边;
(2)先求出所有数值绝对值的和,再乘以0.0642即可.
25.最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加,小明家新换了一辆新能源汽车,他连续7天记录了每天行驶的路程(如表).以为标准,多于的记为“+”,不足的记为“-”,刚好的记为“”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程()
(1)这天里路程最多的一天比最少的一天多走______km;(答案直接填写在答题卡的横线上)
(2)请求出小明家的新能源汽车这七天一共行驶了多少千米?
(3)小明家原来的汽油车每行驶需用汽油升,汽油价元/升.现在的新能源汽车每行驶耗电量为度,每度电为元.请估计小明家换成新能源汽车后这天的行驶费用比原来节省多少钱?
【答案】(1)
(2)千米
(3)元
【分析】本题主要考查了有理数的减法应用,解题的关键是掌握有理数的加减运算,有理数的乘除运算,根据有理数的混合运算,进行解答,即可.
(1)根据有理数的减法列式计算即可;
(2)将天的里程求和,即可得解;
(3)用汽油车的费用减去电车的费用,即可得解.
【详解】(1)解:由表格可知,,
∴这 天里路程最多的一天比最少的一天多走.
故答案为:.
(2)解:,
答:小明家的新能源汽车这七天一共行驶了千米.
(3)解:
答:小明家换成新能源汽车后这天的行驶费用比原来节省元.
同课章节目录
