《高考快车道》2026版高三一轮总复习(数学)58 第七章 第1课时 基本立体图形、简单几何体的表面积与体积
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习(数学)58 第七章 第1课时 基本立体图形、简单几何体的表面积与体积 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 11:49:24 | ||
图片预览








文档简介
(共100张PPT)
第七章 立体几何与空间向量
第七章 立体几何与空间向量
[教师备选资源]
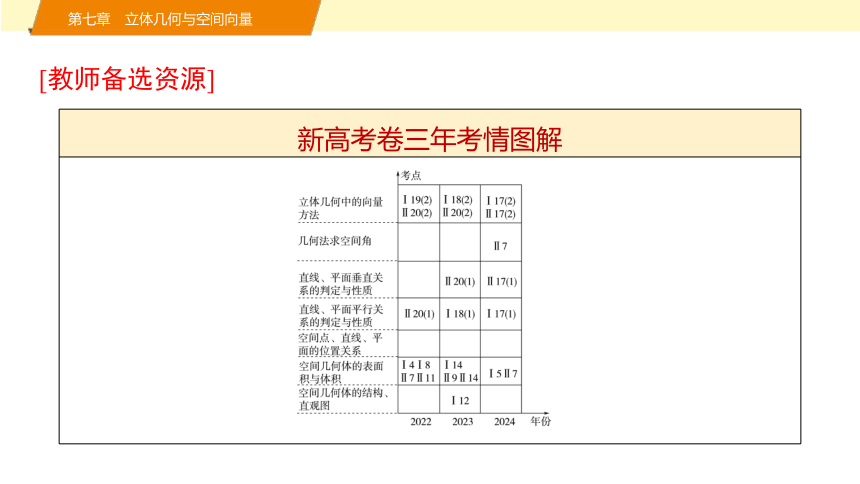
新高考卷三年考情图解
第七章 立体几何与空间向量
高考命题规律把握
1.常考点:空间几何体的表面积与体积、空间线面位置关系的证明、立体几何中的向量方法.
空间几何体的表面积与体积主要考小题:一是柱、锥、台体的体积与表面积的计算,二是球与柱、锥、台体的切接问题;空间线面位置关系的证明与立体几何中的向量方法主要考解答题,第(1)问重点考查线面位置关系的证明;第(2)问重点考查空间角,尤其是二面角、线面角的计算.
2.轮考点:空间几何体的结构.
常与数学文化结合以客观题的形式出现,主要考查对空间几何体的结构认知,难度较小.
第1课时
基本立体图形、简单几何体的表面积与体积
[考试要求] 1.认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构.
2.掌握球、棱(圆)柱、棱(圆)锥、棱(圆)台的表面积和体积的计算公式,能用公式解决简单的实际问题.
3.能用斜二测画法画出简单空间图形的直观图.
链接教材·夯基固本
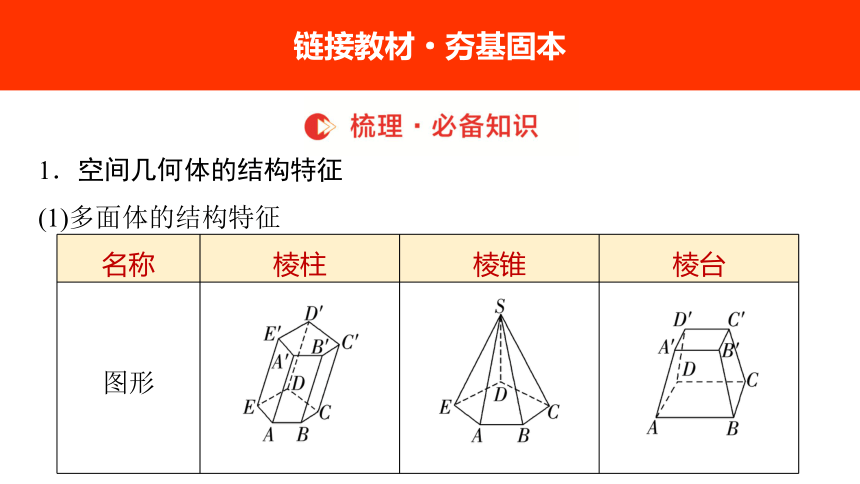
1.空间几何体的结构特征
(1)多面体的结构特征
名称 棱柱 棱锥 棱台
图形
名称 棱柱 棱锥 棱台
底面 互相______且______ 多边形 互相______且______
侧棱 ____________ 相交于______但不一定相等 延长线交于______
侧面 形状 ____________ ________ ______
平行
全等
平行
相似
平行且相等
一点
一点
平行四边形
三角形
梯形
(2)特殊的棱柱
①侧棱垂直于底面的棱柱叫做________.
②侧棱不垂直于底面的棱柱叫做________.
③底面是正多边形的直棱柱叫做________.
④底面是平行四边形的四棱柱叫做____________.
(3)正棱锥
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.特别地,各棱均相等的正三棱锥叫正四面体.
直棱柱
斜棱柱
正棱柱
平行六面体
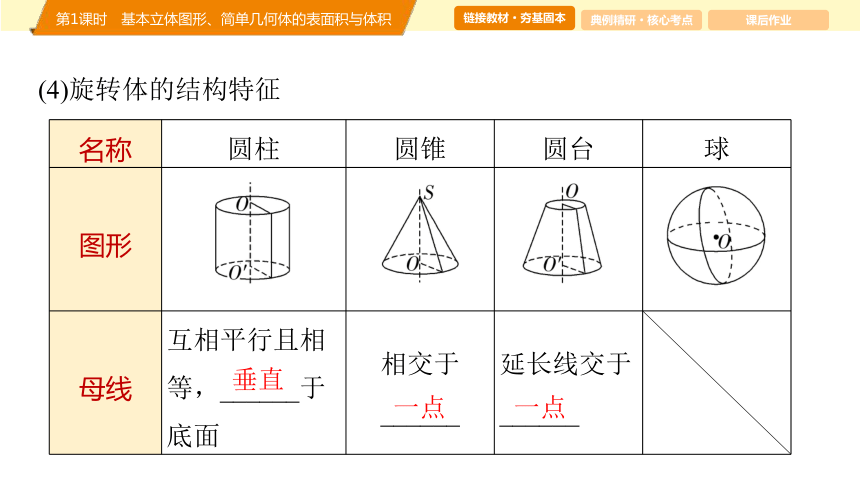
(4)旋转体的结构特征
名称 圆柱 圆锥 圆台 球
图形
母线 互相平行且相等,______于底面 相交于______ 延长线交于______
垂直
一点
一点
轴截面 ______ ____________ __________ ______
侧面 展开图 ______ ______ ______
矩形
等腰三角形
等腰梯形
圆面
矩形
扇形
扇环
2.立体图形的直观图
(1)画法:常用____________.
(2)规则:
①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面______.
②原图形中平行于坐标轴的线段,直观图中仍__________________,平行于x轴和z轴的线段在直观图中保持原长度______,平行于y轴的线段在直观图中长度变为原来的______.
斜二测画法
垂直
分别平行于坐标轴
不变
一半
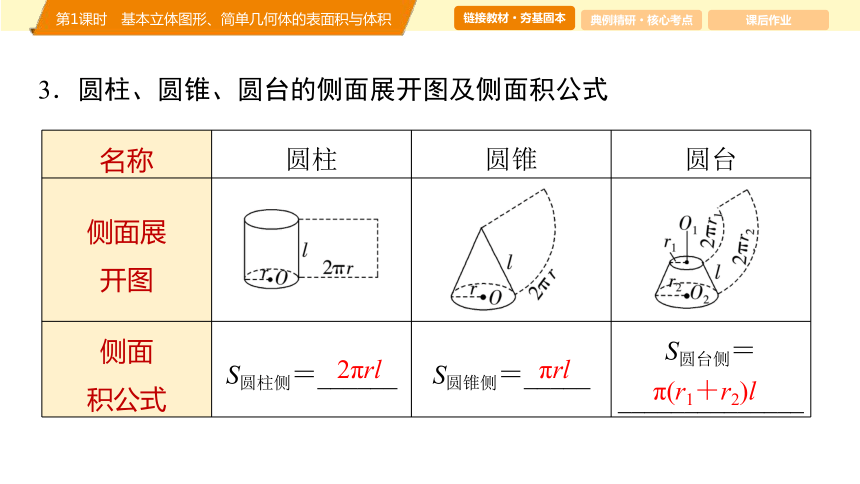
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
名称 圆柱 圆锥 圆台
侧面展 开图
侧面 积公式 S圆柱侧=______ S圆锥侧=_____ S圆台侧=
______________
2πrl
πrl
π(r1+r2)l
4.柱、锥、台、球的表面积和体积
名称 表面积 体积
柱体(棱柱和圆柱) S表面积=S侧+2S底 V=____
锥体(棱锥和圆锥) S表面积=S侧+S底 V=_______
台体(棱台和圆台) S表面积=S侧+S上+S下 V=(S上+S下+)h
球 S=______ V=_________
Sh
Sh
4πR2
πR3
[常用结论]
1.与体积有关的几个结论
(1)一个组合体的体积等于它的各部分体积的和或差.
(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).
2.直观图与原平面图形面积间的关系:S直观图=S原图,S原图=2S直观图.
一、易错易混辨析(正确的打“√”,错误的打“×”)
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.
( )
(2)菱形的直观图仍是菱形. ( )
(3)两个球的体积之比等于它们的半径比的平方. ( )
×
×
×
√
二、教材经典衍生
1.(人教A版必修第二册P119例4改编)已知圆柱的底面直径和高都等于球的直径,则球与圆柱的表面积之比为( )
A.1∶1 B.2∶1
C.3∶2 D.2∶3
D [设球的半径为r,则S圆柱=2πr2+2πr·2r=6πr2,S球=4πr2,所以球的表面积与圆柱的表面积之比为4πr2∶6πr2=2∶3,故选D.]
2.(人教A版必修第二册P106习题8.1T8改编)如图所示,长方体ABCD-A′B′C′D′被一个平面截去一部分,其中EH∥A′D′,则剩下的几何体是( )
A.棱台 B.四棱柱
C.五棱柱 D.简单组合体
√
C [由几何体的结构特征知,剩下的几何体为五棱柱.]
3.(人教A版必修第二册P119练习T1改编)已知圆锥的表面积为
12π cm2,其侧面展开图是一个半圆,则圆锥底面圆的半径为( )
A.1 cm B.2 cm
C.3 cm D. cm
√
B [设圆锥的底面圆的半径为r,母线长为l,因为侧面展开图是一个半圆,所以πl=2πr,即l=2r,所以πr2+πrl=πr2+πr·2r=3πr2=12π,解得r=2(cm).]
4.(人教A版必修第二册P120习题8.3T3改编)如图,一个直三棱柱形容器中盛有水,侧棱AA1=16.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.当底面ABC水平放置时,液面高为________.
12
12 [设△ABC的面积为a,底面ABC水平放置时,液面高为h,侧面AA1B1B水平放置时,水的体积为V=S△ABC·AA1=a·16=12a,
当底面ABC水平放置时,水的体积为V=S△ABCh=ah,于是ah=12a,解得h=12,
所以当底面ABC水平放置时,液面高为12.]
考点一 基本立体图形
考向1 结构特征
[典例1] (多选)下列说法中正确的是( )
A.以直角梯形垂直于底边的腰所在直线为旋转轴,其余边旋转一周形成的几何体是圆台
B.各侧面都是正方形的四棱柱一定是正方体
C.底面是正多边形的棱锥是正棱锥
D.棱台的各侧棱延长后必交于一点
典例精研·核心考点
√
√
AD [由圆台定义知,以直角梯形垂直于底边的腰所在直线为旋转轴,其余三边旋转一周形成的几何体是圆台,故A正确;
各侧面都是正方形的四棱柱中,如果底面是菱形,不一定是正方体,故B错误;
底面是正多边形的棱锥,不能保证顶点在底面上的射影为底面正多边形的中心,故C错误;
棱台是由平行于棱锥底面的平面截得的,故棱台的各侧棱延长后必交于一点,故D正确.故选AD.]
考向2 直观图
[典例2] 如图,四边形ABCD的斜二测画法直观图为等腰梯形A′B′C′D′.已知A′B′=4,C′D′=2,则下列说法正确的是( )
A.AB=2
B.A′D′=2
C.四边形ABCD的周长为4+2+2
D.四边形ABCD的面积为6
√
D [由题意可知A′D′=,直观图的原图形如图所示,所以AB=
4,AD=2,CD=2,作CE⊥AB于点E,可求得BC=2.
所以四边形ABCD的周长为6+2+2,四边形ABCD的面积为×2=6.故选D.]
【教用·备选题】
已知正三角形ABC的边长为a,那么△ABC的平面直观图
△A′B′C′的面积为( )
A.a2 B.a2 C.a2 D.a2
√
D [法一:如图①②所示的原图形和直观图,
由图②可知,A′B′=AB=a,O′C′=OC=a,
在图②中作C′D′⊥A′B′于点D′,
则C′D′=O′C′=a,所以S△A′B′C′=A′B′×C′D′=×a×a=a2.故选D.
法二:S△ABC=×a×a sin 60°=a2,
又S直观图=S原图=a2=a2.故选D.]
考向3 展开图
[典例3] 如图所示,在正三棱柱ABC-A1B1C1中,AB=2,AA1=2,由顶点B沿棱柱侧面(经过棱AA1)到达顶点C1,与AA1的交点记为M,则从点B经点M到C1的最短路线长为( )
A.2 B.2
C.4 D.4
√
B [如图,沿侧棱BB1将正三棱柱的侧面展开,
由侧面展开图可知,当B,M,C1三点共线时,从点B经点M到C1的路线最短.
所以最短路线长为BC1==2.故选B.]
【教用·备选题】
如图,正三棱柱ABC-A1B1C1的侧棱长为a,底面边长为b,一只蚂蚁从点A出发沿每个侧面爬到A1,路线为A→M→N→A1,则蚂蚁爬行的最短路程是( )
A.
B.
C.
D.
√
A [正三棱柱的侧面展开图是如图所示的矩形,矩形的长为3b,宽为a,则其对角线AA1的长为最短路程.因此蚂蚁爬行的最短路程为.故选A.]
名师点评 (1)空间几何体结构特征的判断技巧:紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.
(2)在斜二测画法中,平行于x轴或在x轴上的线段平行性不变,长度不变;平行于y轴或在y轴上的线段平行性不变,长度减半.
(3)在解决空间几何体最短距离问题时,一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.
[跟进训练]
1.(1)(多选)下列说法中正确的是( )
A.长方体是直四棱柱
B.两个面平行,其余各面是梯形的多面体是棱台
C.正棱锥的侧面是全等的等腰三角形
D.平行六面体不是棱柱
√
√
(2)在我国古代数学名著《数学九章》中有这样一个问题:“今有木长二丈四尺,围之五尺.葛生其下,缠本两周,上与木齐,问葛长几何?”意思是:“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”(注:1丈等于10尺),则这个问题中,葛藤长的最小值为( )
A.2丈4尺 B.2丈5尺
C.2丈6尺 D.2丈8尺
√
(3)(多选)(2025·河北冀州中学期中)如图所示,用斜二测画法画一个水平放置的△ABC的直观图,OA=2,S△ABC=,则在直观图中,以下说法正确的是( )
A.O′A′=2
B.△A′B′C′的面积为
C.OA边上的高为
D.O′A′边上的高为
√
√
√
(1)AC (2)C (3)ABC [(1)长方体是直四棱柱,A正确;两个平面平行,其余各面是梯形的多面体,当侧棱延长后不交于同一点时,就不是棱台,B错误;正棱锥的侧面是全等的等腰三角形,C正确;平行六面体是棱柱,D错误.故选AC.
(2)如图,由题意,圆柱的侧面展开图是矩形ABEF,圆木的高AB=24尺,BE=5尺,因此葛藤绕圆木2周后长度最小为BD===26(尺),即为2丈6尺.故选C.
(3)由题意知O′A′=OA=2,所以A正确;
在△ABC中,过B作BD∥y轴,交x轴于点D如图①,在直观图中的x′轴上取O′D′=OD,
连接D′B′,如图②,则D′B′=DB,
由于BD⊥AC于点D,则BD为原图形中OA边上的高,且BD=2B′D′,S△ABC=AC×BD=,BD=2B′D′=,所以C正确;
在直观图中作B′E′⊥A′C′于点E′,B′D′=B′E′=,B′E′=,所以D错误;
S△A′B′C′=A′C′×B′E′=,所以B正确.
故选ABC.]
【教用·备选题】
1.已知圆锥的母线长为1,其侧面展开图是一个圆心角为120°的扇形,则该圆锥的轴截面面积为( )
A. B. C. D.
√
B [因为圆锥的母线长为1,其侧面展开图是一个圆心角为120°的扇形,所以圆锥的底面周长为1×=,所以底面半径为,高为=,所以轴截面面积为=.故选B.]
2.多面体欧拉定理是指对于简单多面体,其各维对象数总满足一定的数量关系,在三维空间中,多面体欧拉定理可表示为:V(顶点数)+F(表面数)-E(棱长数)=2.在数学上,富勒烯的结构都是以正五边形和正六边形面组成的凸多面体,例如富勒烯C60(结构图如图)是用碳原子组成的稳定分子,具有60个顶点和32个面,其中12个面为正五边形,20个面为正六边形.除C60外具有封闭笼
状结构的富勒烯还可能有C28,C32,C50,C70,C84,
C240,C540等,则C84结构含有正六边形的个数为( )
A.12 B.24 C.30 D.32
√
D [设C84结构中形状为正五边形和正六边形的面各有x个和y个,
V=84,F=x+y,E=3×84÷2.
由欧拉公式V+F-E=2,可得84+x+y-3×84÷2=2,即x+y=44.
又由多边形的边数可表示C84的棱数,
即(5x+6y)÷2=3×84÷2,即5x+6y=252,
由解得
故C84结构含有正六边形的个数为32.]
考点二 空间几何体的表面积与体积
考向1 表面积
[典例4] (1)(2020·全国Ⅰ卷)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π
C.36π D.32π
√
(2)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为2∶3,则正六棱锥与正六棱柱的侧面积的比值为( )
A. B.
C. D.
√
(1)A (2)B [(1)如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,又AB=BC=AC=OO1,所以=2r,解得AB=2,故OO1=2,所以R2=+r2=(2)2+22=16,所以球O的表面积S=4πR2=64π.故选A.
(2)设正六棱柱的底面边长为a,由题意知正六棱柱的高为2a,因为正六棱锥的高与底面边长的比为2∶3,所以正六棱锥的高为a,正六棱锥的侧棱长为a,正六棱锥的侧面积
S1=6×a=a2,
正六棱柱的侧面积S2=6·a·2a=12a2,所以=.故选B.]
考向2 体积
[典例5] (1)(2024·新高考Ⅰ卷)已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为,则圆锥的体积为( )
A.2π B.3π
C.6π D.9π
√
(2)(2024·天津模拟)如图,在斜三棱柱ABC-A1B1C1中,O为四边形ACC1A1对角线的交点,设三棱柱ABC-A1B1C1的体积为V1,四棱锥
O-BCC1B1的体积为V2,则V2∶V1=( )
A.1∶3 B.1∶4
C.1∶6 D.2∶3
(3)(2023·新高考Ⅰ卷)在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,AA1=,则该棱台的体积为________.
√
(1)B (2)A (3) [(1)设圆柱和圆锥的底面半径均为r,则圆锥的母线长为,而它们的侧面积相等,所以2πr×=πr×,即2=,故r=3,故圆锥的体积为π×9×=3π.故选B.
(2)如图,连接OA1,A1B,
则V1=,
=V1,
所以=V1,
又O为A1C的中点,
所以点A1到平面BCC1B1的距离是点O到平面BCC1B1的距离的2倍,则==2V2,
所以V1=2V2,即=.故选A.
(3)法一:如图所示,设O1,O分别为正四棱台ABCD-A1B1C1D1上、下底面的中心,连接B1D1,BD,则O1,O分别为B1D1,BD的中点,连接O1O,则O1O即是正四棱台ABCD-A1B1C1D1的高,过点B1作B1E⊥BD,垂足为E,则B1E=O1O.因为AB=2,A1B1=1,所以OB=,O1B1=,所以BE=OB-OE=OB-O1B1=,又AA1=,所以BB1=,B1E===,所以O1O=,所以=×
(22+12+)×=.
法二:如图,将正四棱台ABCD-A1B1C1D1补形成正四棱锥P-ABCD,因为AB=2,A1B1=1,AB∥A1B1,所以A1,B1,C1,D1分别为PA,PB,PC,PD的中点,又A1A=,所以PA=2,即PB=2.连接BD,取BD的中点为O,连接PO,则PO⊥平面
ABCD,易知BO=,所以PO=
=,所以正四棱台ABCD-A1B1C1D1
的高为,所以=×
(22+12+)×=.(或者V四棱锥P-ABCD=×22×=,
=V四棱锥P-ABCD,所以=
V四棱锥P-ABCD-=V四棱锥P-ABCD==.)]
名师点评 求空间几何体的体积的常用方法
公式法 规则几何体的体积问题,直接利用公式进行求解
割补法 把不规则的几何体分割成规则的几何体,或者补成规则的几何体,再求解
等体 积法 通过选择合适的底面来求几何体的体积,特别是三棱锥的体积(即利用三棱锥的任一个面均可作为三棱锥的底面,进行等体积变换)
[跟进训练]
2.(1)(2024·山东枣庄一模)已知圆台的上、下底面半径分别为1和3,侧面展开图是半个圆环,则圆台的侧面积为( )
A.6π B.16π
C.26π D.32π
√
(2)(2024·北京西城二模)楔体形构件在建筑工程上有广泛的应用.如图,某楔体形构件可视为一个五面体ABCDEF,其中平面ABCD为正方形.若AB=6 cm,EF=3 cm,且EF与平面ABCD的距离为2 cm,则该楔体形构件的体积为( )
A.18 cm3 B.24 cm3
C.30 cm3 D.48 cm3
(3)(2020·新高考Ⅱ卷)棱长为2的正方体ABCD-A1B1C1D1中,M,N分别为棱BB1,AB的中点,则三棱锥A1-D1MN的体积为________.
√
1
(1)B (2)C (3)1 [(1)圆台的上底面圆半径r′=1,下底面圆半径r=3,
设圆台的母线长为l,扇环所在的小圆的半径为x,依题意有解得所以圆台的侧面积S=πl=π×4=16π.故选B.
(2)如图所示,设G,H分别为AB,DC的中点,连接EG,EH,GH,
因为底面ABCD为正方形,所以AB∥DC,又AB 平面EFCD,DC 平面EFCD,所以AB∥平面EFCD,
又平面EFCD∩平面ABFE=EF,所以AB∥EF,
因为G,H分别为AB,DC的中点,AB=6 cm,EF=3 cm,
所以EF∥GB,EF=GB,则四边形EGBF为平行四边形,则EG∥FB,
同理EH∥FC,又GH∥BC,所以EGH-FBC为三棱柱,由题意,可得V四棱锥E-AGHD=S矩形AGHD·h=AD·AG·h=×6×3×2=12(cm3).
又V三棱柱EGH-FBC=3V三棱锥B-EGH=3V三棱锥E-BGH=3××V四棱锥E-AGHD=·V四棱锥E-AGHD=×12=18(cm3).
所以该多面体的体积为V=V四棱锥E-AGHD+V三棱柱EGH-FBC=12+18=30(cm3).故选C.
(3)如图,易知=,由正方体的结构特征,知D1A1⊥平面A1MN,所以D1A1为三棱锥D1-A1MN的高.因为M,N分别为棱BB1,AB的中点,所以=2×2-×1×1-×1×2-×1×2=,所以==××D1A1=×2=1.]
【教用·备选题】
1.(2024·辽宁大连一模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知底面圆的直径AB=12 cm,圆柱体部分的高BC=6 cm,圆锥体部分的高CD=4 cm,则这个陀螺的表面积(单位:cm2)为
( )
A.π B.π
C.π D.π
√
C [由题意可知,圆锥的母线长为=2,
所以这个陀螺的表面积为π×62+2π×6×6+π×2×6=π.
故选C.]
2.《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”意思为:今有底面为矩形的屋脊形状的多面体(如图),下底面宽AD=3丈,长AB=4丈,上棱EF=2丈,EF与平面ABCD平行,EF与平面ABCD的距离为1丈,则它的体积是( )
A.4立方丈 B.5立方丈
C.6立方丈 D.8立方丈
√
B [如图,过点E作EG⊥平面ABCD,垂足为点G,过点F作FH⊥平面ABCD,垂足为点H,过点G作PQ∥AD,交AB于点Q,交CD于点P,过点H作MN∥BC,交AB于点N,交CD于点M,连接EQ,EP,FN,FM.则AQ+NB=4-2=2,QN=2,且四边形AQPD与四边形NBCM都是矩形.
则它的体积V=VE-AQPD+VEPQ-FMN+VF-NBCM=·EG·S矩形AQPD+S△EPQ·NQ+·FH·S矩形NBCM=(AQ+NB)·AD·EG+S△EPQ·NQ=×2×3×1+×3×1×2=5(立方丈).]
3.(2024·江苏常州模拟)如图,圆锥的底面半径为1,侧面展开图是圆心角为60°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为,则圆台的侧面积为
( )
A. B.
C. D.8π
√
C [设圆锥的半径为R,母线长为l,则R=1.设圆台的上底面半径为r,母线长为l1,则r=.
由已知可得,==,所以l=6.
如图,作出圆锥、圆台的轴截面,
则有==,所以l1=4.
所以圆台的侧面积为π(R+r)l1=4×π=π.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
一、单项选择题
1.(2025·陕西西安模拟)乒乓球被誉为我国的“国球”,一个标准尺寸乒乓球的直径是40 mm,则其表面积约为( )
A.3 000 mm2 B.4 000 mm2
C.5 000 mm2 D.6 000 mm2
13
课后作业(三十八) 基本立体图形、简单几何体的表面积与体积
√
14
C [标准尺寸乒乓球的直径是40 mm,标准乒乓球的半径R=20 mm,故表面积S=4πR2≈5 000 mm2.故选C. ]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
2.(2024·广西来宾一模)已知一个正四棱台的上、下底面边长分别为1,2,体积为3,则该正四棱台的高为( )
A.1 B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
D [设该正四棱台的高为h,
又其上、下底面边长分别为1,2,体积为3,
则V=h(12+22+)==3,
所以h=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
3.水平放置的四边形ABCD的直观图是直角梯形A′B′C′D′,如图所示.其中B′C′=A′B′=1,则原平面图形的面积为( )
A. B.
C.3 D.6
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
C [在直角梯形A′B′C′D′中,B′C′=A′B′=1,且∠A′D′C′=45°,作A′P⊥D′C′于点P,
则四边形A′B′C′P为正方形,△A′PD′为等腰直角三角形,
故A′D′=,D′C′=2.
故原图形为直角梯形,且上底AB=A′B′=1,高AD=2A′D′=2,下底DC=D′C′=2.
其面积为×2=3.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
4.(2024·山西晋城二模)已知圆锥的侧面积为12π,它的侧面展开图是圆心角为的扇形,则此圆锥的体积为( )
A.6π B.
C.6π D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
B [设圆锥的底面半径为r,母线长为l,
由题意可得解得l=6,r=2,
则圆锥的高h==4,
所以此圆锥的体积为h×πr2=.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
5.将12根长度相同的小木棍通过黏合端点的方式拼接(不可折断,可以不全部用完),不可能拼成( )
A.正三棱柱 B.正四棱锥
C.正四棱柱 D.正六棱锥
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
D [正三棱柱中9条棱的长度可以相等,A成立;
正四棱锥中8条棱的长度可以相等,B成立;
正四棱柱中12条棱的长度可以相等,C成立;
因为正六边形的中心到六个顶点的距离都等于边长,
所以正六棱锥的侧棱总比底边长,D不成立.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
6.(2023·天津高考)在三棱锥P-ABC中,线段PC上的点M满足PM=PC,线段PB上的点N满足PN=PB,则三棱锥P-AMN和三棱锥P-ABC的体积之比为( )
A. B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
B [如图,因为PM=PC,PN=PB,所以====,所以====(其中d为点A到平面PBC的距离,因为平面PMN和平面PBC重合,所以点A到平面PMN的距离也为d).
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
二、多项选择题
7.如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,将容器以BC为轴顺时针旋转,则( )
A.有水的部分始终是棱柱
B.水面所在四边形EFGH为矩形且面积不变
C.棱A1D1始终与水面平行
D.当点H在棱CD上且点G在棱CC1上(均不含端点)时,
BE·BF不是定值
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
AC [对于A,有水的部分的几何体,有两个面都垂直于BC,这两个面始终平行,而AD∥BC,
并且BC始终与水面平行,即有FG∥BC,若点H在棱DD1上,由面面平行的性质知,
EH∥FG,若点H在棱CD上,EH∥BC,因此该几何体有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边互相平行,即该几何体是棱柱,A正确;
对于B,因为水面EFGH为矩形,边FG的长度不变,EF随旋转角的变化而变化,矩形EFGH的面积不是定值,B错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于C,因为A1D1始终与BC平行,而BC始终与水面平行,并且A1D1不在水面所在平面内,即棱A1D1始终与水面平行,C正确;
对于D,当点H在棱CD上且点G在棱CC1上(均不含端点)时,有水部分的棱柱的底面为三角形,
而水的体积不变,高BC不变,则底面面积BE·BF不变,即BE·BF为定值,D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
8.(2024·江苏徐州一模)已知圆台的上、下底面直径分别为2,6,高为2,则( )
A.该圆台的体积为26π
B.该圆台外接球的表面积为π
C.用过任意两条母线的平面截该圆台所得截面周长的最大值为16
D.挖去以该圆台上底面为底,高为的圆柱后所得几何体的表面积为π
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
BC [由已知得圆台的上、下底面半径分别为1,3,
对于A,圆台的体积为π×2=π,A错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于B,如图是圆台的轴截面ABCD,外接球球心为O,设外接球半径为R,
当球心在梯形ABCD内时,=2,解得R2=,
当球心在梯形ABCD外时(图略),=2,方程无解,
所以外接球的表面积为4πR2=π,B正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于C,用过任意两条母线的平面截该圆台所得截面中,轴截面的周长最大,
又母线长为=4,则最大周长为4+4+2+6=16,C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于D,如图,挖去以该圆台上底面为底,高为的圆柱后所得几何体的表面积为
π×4+2π×1×+π×=26π+2π,D错误.
故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
三、填空题
9.如图,四边形OABC是边长为1的正方形,是四分之一圆,则图中阴影部分以OC所在直线为旋转轴旋转一周得到的旋转体的表面积为________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
5π
5π [该旋转体是一个圆柱挖去一个半球后剩余的部分,且圆柱的底面半径是1,高是1,球的半径是1,所以该旋转体的表面积为π×12+2π×1×1+×4π×12=5π.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
10.(人教A版必修第二册P116练习T3改编)某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的(如图),则该几何体共有_____个面;若被截正方体的棱长是60 cm,那么该石凳的表面积是_________________cm2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
14
10 800+3 600
14 10 800+3 600 [由题意知,截去的八个四面体是全等的正三棱锥,石凳的8个面为三角形,6个面为正方形,所以该几何体共有14个面;
如果被截正方体的棱长是60 cm,那么石凳的表面积是
S=8××30×30×sin 60°+6×30×30=.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
11.(2025·陕西安康模拟)随着古代瓷器工艺的高速发展,在著名的宋代五大名窑之后,又增加了三种瓷器,与五大名窑并称为中国八大名瓷,其中最受欢迎的是景德镇窑.如图,景德镇产的青花玲珑瓷(无盖)的形状可视为一个球被两个平行平面所截后剩下的部分,其中球面被平面所截的部分均可视为球冠(截得的圆面是底,垂直于圆面的直径被截得的部分是高,其面积公式为S=2πRh,其中R为球的半径,h为球冠的高).已知瓷器的高为38 cm,在高为20 cm处有最大直径(外径)为48 cm,则该瓷器的外表面积约为(π取3.14) ( )
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
A.6 270 cm2
B.6 275 cm2
C.6 280 cm2
D.6 300 cm2
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
C [由题意可知,球的半径为R=24 cm,上球冠的高h1=6 cm,下球冠的高h2=4 cm,
设下底面圆的半径为r,则r2=242-202=176,
所以该瓷器的外表面积为4π×242-2π×24×6-2π×24×4+π×176=
2 000π≈6 280.
故选C.]
12.(2025·陕西西安模拟)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商准备将棱长为8 cm的正四面体的魔方放入正方体盲盒内,为节约成本,使得魔方能够放入盲盒且盲盒棱长最小,则盲盒内剩余空间的体积为( )
A. cm3 B. cm3
C. cm3 D. cm3
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
C [依题意,要将棱长为8 cm的正四面体的魔方放入正方体盲盒内,且盲盒棱长最小,则当且仅当正方体的面对角线长等于正四面体的棱长,即它们有相同的外接球,
如图,正四面体ABCD的棱长为8 cm,
所以该正方体的棱长为4 cm,盲盒内剩余空间
的体积为4××4×4×4=(cm3).故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
13.(多选)(2022·新高考Ⅱ卷)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则( )
A.V3=2V2
B.V3=V1
C.V3=V1+V2
D.2V3=3V1
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
CD [设AB=ED=2FB=2,则V1=×2×2×2=,V2=×2×2×1=.连接BD交AC于点M,连接EM,FM(图略),则FM=,EM=,EF=3,则FM2+EM2=EF2,故S△EMF==,V3=×AC=2,V3=V1+V2,2V3=3V1,故选CD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
14.(2024·九省联考)已知轴截面为正三角形的圆锥的高与球O的直径相等,则圆锥的体积与球O的体积的比值是________,圆锥的表面积与球O的表面积的比值是________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
1 [设圆锥的底面半径为r,球的半径为R,
因为圆锥的轴截面为正三角形,所以圆锥的高h=r,母线长l=2r,由题可知,h=2R,所以球的半径R=r,
1
所以圆锥的体积为V1=×π×r2×r=πr3,
球的体积V2=πR3=π×=πr3,
所以==.
圆锥的表面积S1=πrl+πr2=3πr2,
球的表面积S2=4πR2=4π×=3πr2,
所以==1.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
谢 谢!
第七章 立体几何与空间向量
第七章 立体几何与空间向量
[教师备选资源]
新高考卷三年考情图解
第七章 立体几何与空间向量
高考命题规律把握
1.常考点:空间几何体的表面积与体积、空间线面位置关系的证明、立体几何中的向量方法.
空间几何体的表面积与体积主要考小题:一是柱、锥、台体的体积与表面积的计算,二是球与柱、锥、台体的切接问题;空间线面位置关系的证明与立体几何中的向量方法主要考解答题,第(1)问重点考查线面位置关系的证明;第(2)问重点考查空间角,尤其是二面角、线面角的计算.
2.轮考点:空间几何体的结构.
常与数学文化结合以客观题的形式出现,主要考查对空间几何体的结构认知,难度较小.
第1课时
基本立体图形、简单几何体的表面积与体积
[考试要求] 1.认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构.
2.掌握球、棱(圆)柱、棱(圆)锥、棱(圆)台的表面积和体积的计算公式,能用公式解决简单的实际问题.
3.能用斜二测画法画出简单空间图形的直观图.
链接教材·夯基固本
1.空间几何体的结构特征
(1)多面体的结构特征
名称 棱柱 棱锥 棱台
图形
名称 棱柱 棱锥 棱台
底面 互相______且______ 多边形 互相______且______
侧棱 ____________ 相交于______但不一定相等 延长线交于______
侧面 形状 ____________ ________ ______
平行
全等
平行
相似
平行且相等
一点
一点
平行四边形
三角形
梯形
(2)特殊的棱柱
①侧棱垂直于底面的棱柱叫做________.
②侧棱不垂直于底面的棱柱叫做________.
③底面是正多边形的直棱柱叫做________.
④底面是平行四边形的四棱柱叫做____________.
(3)正棱锥
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.特别地,各棱均相等的正三棱锥叫正四面体.
直棱柱
斜棱柱
正棱柱
平行六面体
(4)旋转体的结构特征
名称 圆柱 圆锥 圆台 球
图形
母线 互相平行且相等,______于底面 相交于______ 延长线交于______
垂直
一点
一点
轴截面 ______ ____________ __________ ______
侧面 展开图 ______ ______ ______
矩形
等腰三角形
等腰梯形
圆面
矩形
扇形
扇环
2.立体图形的直观图
(1)画法:常用____________.
(2)规则:
①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面______.
②原图形中平行于坐标轴的线段,直观图中仍__________________,平行于x轴和z轴的线段在直观图中保持原长度______,平行于y轴的线段在直观图中长度变为原来的______.
斜二测画法
垂直
分别平行于坐标轴
不变
一半
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
名称 圆柱 圆锥 圆台
侧面展 开图
侧面 积公式 S圆柱侧=______ S圆锥侧=_____ S圆台侧=
______________
2πrl
πrl
π(r1+r2)l
4.柱、锥、台、球的表面积和体积
名称 表面积 体积
柱体(棱柱和圆柱) S表面积=S侧+2S底 V=____
锥体(棱锥和圆锥) S表面积=S侧+S底 V=_______
台体(棱台和圆台) S表面积=S侧+S上+S下 V=(S上+S下+)h
球 S=______ V=_________
Sh
Sh
4πR2
πR3
[常用结论]
1.与体积有关的几个结论
(1)一个组合体的体积等于它的各部分体积的和或差.
(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).
2.直观图与原平面图形面积间的关系:S直观图=S原图,S原图=2S直观图.
一、易错易混辨析(正确的打“√”,错误的打“×”)
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.
( )
(2)菱形的直观图仍是菱形. ( )
(3)两个球的体积之比等于它们的半径比的平方. ( )
×
×
×
√
二、教材经典衍生
1.(人教A版必修第二册P119例4改编)已知圆柱的底面直径和高都等于球的直径,则球与圆柱的表面积之比为( )
A.1∶1 B.2∶1
C.3∶2 D.2∶3
D [设球的半径为r,则S圆柱=2πr2+2πr·2r=6πr2,S球=4πr2,所以球的表面积与圆柱的表面积之比为4πr2∶6πr2=2∶3,故选D.]
2.(人教A版必修第二册P106习题8.1T8改编)如图所示,长方体ABCD-A′B′C′D′被一个平面截去一部分,其中EH∥A′D′,则剩下的几何体是( )
A.棱台 B.四棱柱
C.五棱柱 D.简单组合体
√
C [由几何体的结构特征知,剩下的几何体为五棱柱.]
3.(人教A版必修第二册P119练习T1改编)已知圆锥的表面积为
12π cm2,其侧面展开图是一个半圆,则圆锥底面圆的半径为( )
A.1 cm B.2 cm
C.3 cm D. cm
√
B [设圆锥的底面圆的半径为r,母线长为l,因为侧面展开图是一个半圆,所以πl=2πr,即l=2r,所以πr2+πrl=πr2+πr·2r=3πr2=12π,解得r=2(cm).]
4.(人教A版必修第二册P120习题8.3T3改编)如图,一个直三棱柱形容器中盛有水,侧棱AA1=16.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.当底面ABC水平放置时,液面高为________.
12
12 [设△ABC的面积为a,底面ABC水平放置时,液面高为h,侧面AA1B1B水平放置时,水的体积为V=S△ABC·AA1=a·16=12a,
当底面ABC水平放置时,水的体积为V=S△ABCh=ah,于是ah=12a,解得h=12,
所以当底面ABC水平放置时,液面高为12.]
考点一 基本立体图形
考向1 结构特征
[典例1] (多选)下列说法中正确的是( )
A.以直角梯形垂直于底边的腰所在直线为旋转轴,其余边旋转一周形成的几何体是圆台
B.各侧面都是正方形的四棱柱一定是正方体
C.底面是正多边形的棱锥是正棱锥
D.棱台的各侧棱延长后必交于一点
典例精研·核心考点
√
√
AD [由圆台定义知,以直角梯形垂直于底边的腰所在直线为旋转轴,其余三边旋转一周形成的几何体是圆台,故A正确;
各侧面都是正方形的四棱柱中,如果底面是菱形,不一定是正方体,故B错误;
底面是正多边形的棱锥,不能保证顶点在底面上的射影为底面正多边形的中心,故C错误;
棱台是由平行于棱锥底面的平面截得的,故棱台的各侧棱延长后必交于一点,故D正确.故选AD.]
考向2 直观图
[典例2] 如图,四边形ABCD的斜二测画法直观图为等腰梯形A′B′C′D′.已知A′B′=4,C′D′=2,则下列说法正确的是( )
A.AB=2
B.A′D′=2
C.四边形ABCD的周长为4+2+2
D.四边形ABCD的面积为6
√
D [由题意可知A′D′=,直观图的原图形如图所示,所以AB=
4,AD=2,CD=2,作CE⊥AB于点E,可求得BC=2.
所以四边形ABCD的周长为6+2+2,四边形ABCD的面积为×2=6.故选D.]
【教用·备选题】
已知正三角形ABC的边长为a,那么△ABC的平面直观图
△A′B′C′的面积为( )
A.a2 B.a2 C.a2 D.a2
√
D [法一:如图①②所示的原图形和直观图,
由图②可知,A′B′=AB=a,O′C′=OC=a,
在图②中作C′D′⊥A′B′于点D′,
则C′D′=O′C′=a,所以S△A′B′C′=A′B′×C′D′=×a×a=a2.故选D.
法二:S△ABC=×a×a sin 60°=a2,
又S直观图=S原图=a2=a2.故选D.]
考向3 展开图
[典例3] 如图所示,在正三棱柱ABC-A1B1C1中,AB=2,AA1=2,由顶点B沿棱柱侧面(经过棱AA1)到达顶点C1,与AA1的交点记为M,则从点B经点M到C1的最短路线长为( )
A.2 B.2
C.4 D.4
√
B [如图,沿侧棱BB1将正三棱柱的侧面展开,
由侧面展开图可知,当B,M,C1三点共线时,从点B经点M到C1的路线最短.
所以最短路线长为BC1==2.故选B.]
【教用·备选题】
如图,正三棱柱ABC-A1B1C1的侧棱长为a,底面边长为b,一只蚂蚁从点A出发沿每个侧面爬到A1,路线为A→M→N→A1,则蚂蚁爬行的最短路程是( )
A.
B.
C.
D.
√
A [正三棱柱的侧面展开图是如图所示的矩形,矩形的长为3b,宽为a,则其对角线AA1的长为最短路程.因此蚂蚁爬行的最短路程为.故选A.]
名师点评 (1)空间几何体结构特征的判断技巧:紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.
(2)在斜二测画法中,平行于x轴或在x轴上的线段平行性不变,长度不变;平行于y轴或在y轴上的线段平行性不变,长度减半.
(3)在解决空间几何体最短距离问题时,一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.
[跟进训练]
1.(1)(多选)下列说法中正确的是( )
A.长方体是直四棱柱
B.两个面平行,其余各面是梯形的多面体是棱台
C.正棱锥的侧面是全等的等腰三角形
D.平行六面体不是棱柱
√
√
(2)在我国古代数学名著《数学九章》中有这样一个问题:“今有木长二丈四尺,围之五尺.葛生其下,缠本两周,上与木齐,问葛长几何?”意思是:“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”(注:1丈等于10尺),则这个问题中,葛藤长的最小值为( )
A.2丈4尺 B.2丈5尺
C.2丈6尺 D.2丈8尺
√
(3)(多选)(2025·河北冀州中学期中)如图所示,用斜二测画法画一个水平放置的△ABC的直观图,OA=2,S△ABC=,则在直观图中,以下说法正确的是( )
A.O′A′=2
B.△A′B′C′的面积为
C.OA边上的高为
D.O′A′边上的高为
√
√
√
(1)AC (2)C (3)ABC [(1)长方体是直四棱柱,A正确;两个平面平行,其余各面是梯形的多面体,当侧棱延长后不交于同一点时,就不是棱台,B错误;正棱锥的侧面是全等的等腰三角形,C正确;平行六面体是棱柱,D错误.故选AC.
(2)如图,由题意,圆柱的侧面展开图是矩形ABEF,圆木的高AB=24尺,BE=5尺,因此葛藤绕圆木2周后长度最小为BD===26(尺),即为2丈6尺.故选C.
(3)由题意知O′A′=OA=2,所以A正确;
在△ABC中,过B作BD∥y轴,交x轴于点D如图①,在直观图中的x′轴上取O′D′=OD,
连接D′B′,如图②,则D′B′=DB,
由于BD⊥AC于点D,则BD为原图形中OA边上的高,且BD=2B′D′,S△ABC=AC×BD=,BD=2B′D′=,所以C正确;
在直观图中作B′E′⊥A′C′于点E′,B′D′=B′E′=,B′E′=,所以D错误;
S△A′B′C′=A′C′×B′E′=,所以B正确.
故选ABC.]
【教用·备选题】
1.已知圆锥的母线长为1,其侧面展开图是一个圆心角为120°的扇形,则该圆锥的轴截面面积为( )
A. B. C. D.
√
B [因为圆锥的母线长为1,其侧面展开图是一个圆心角为120°的扇形,所以圆锥的底面周长为1×=,所以底面半径为,高为=,所以轴截面面积为=.故选B.]
2.多面体欧拉定理是指对于简单多面体,其各维对象数总满足一定的数量关系,在三维空间中,多面体欧拉定理可表示为:V(顶点数)+F(表面数)-E(棱长数)=2.在数学上,富勒烯的结构都是以正五边形和正六边形面组成的凸多面体,例如富勒烯C60(结构图如图)是用碳原子组成的稳定分子,具有60个顶点和32个面,其中12个面为正五边形,20个面为正六边形.除C60外具有封闭笼
状结构的富勒烯还可能有C28,C32,C50,C70,C84,
C240,C540等,则C84结构含有正六边形的个数为( )
A.12 B.24 C.30 D.32
√
D [设C84结构中形状为正五边形和正六边形的面各有x个和y个,
V=84,F=x+y,E=3×84÷2.
由欧拉公式V+F-E=2,可得84+x+y-3×84÷2=2,即x+y=44.
又由多边形的边数可表示C84的棱数,
即(5x+6y)÷2=3×84÷2,即5x+6y=252,
由解得
故C84结构含有正六边形的个数为32.]
考点二 空间几何体的表面积与体积
考向1 表面积
[典例4] (1)(2020·全国Ⅰ卷)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π
C.36π D.32π
√
(2)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为2∶3,则正六棱锥与正六棱柱的侧面积的比值为( )
A. B.
C. D.
√
(1)A (2)B [(1)如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,又AB=BC=AC=OO1,所以=2r,解得AB=2,故OO1=2,所以R2=+r2=(2)2+22=16,所以球O的表面积S=4πR2=64π.故选A.
(2)设正六棱柱的底面边长为a,由题意知正六棱柱的高为2a,因为正六棱锥的高与底面边长的比为2∶3,所以正六棱锥的高为a,正六棱锥的侧棱长为a,正六棱锥的侧面积
S1=6×a=a2,
正六棱柱的侧面积S2=6·a·2a=12a2,所以=.故选B.]
考向2 体积
[典例5] (1)(2024·新高考Ⅰ卷)已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为,则圆锥的体积为( )
A.2π B.3π
C.6π D.9π
√
(2)(2024·天津模拟)如图,在斜三棱柱ABC-A1B1C1中,O为四边形ACC1A1对角线的交点,设三棱柱ABC-A1B1C1的体积为V1,四棱锥
O-BCC1B1的体积为V2,则V2∶V1=( )
A.1∶3 B.1∶4
C.1∶6 D.2∶3
(3)(2023·新高考Ⅰ卷)在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,AA1=,则该棱台的体积为________.
√
(1)B (2)A (3) [(1)设圆柱和圆锥的底面半径均为r,则圆锥的母线长为,而它们的侧面积相等,所以2πr×=πr×,即2=,故r=3,故圆锥的体积为π×9×=3π.故选B.
(2)如图,连接OA1,A1B,
则V1=,
=V1,
所以=V1,
又O为A1C的中点,
所以点A1到平面BCC1B1的距离是点O到平面BCC1B1的距离的2倍,则==2V2,
所以V1=2V2,即=.故选A.
(3)法一:如图所示,设O1,O分别为正四棱台ABCD-A1B1C1D1上、下底面的中心,连接B1D1,BD,则O1,O分别为B1D1,BD的中点,连接O1O,则O1O即是正四棱台ABCD-A1B1C1D1的高,过点B1作B1E⊥BD,垂足为E,则B1E=O1O.因为AB=2,A1B1=1,所以OB=,O1B1=,所以BE=OB-OE=OB-O1B1=,又AA1=,所以BB1=,B1E===,所以O1O=,所以=×
(22+12+)×=.
法二:如图,将正四棱台ABCD-A1B1C1D1补形成正四棱锥P-ABCD,因为AB=2,A1B1=1,AB∥A1B1,所以A1,B1,C1,D1分别为PA,PB,PC,PD的中点,又A1A=,所以PA=2,即PB=2.连接BD,取BD的中点为O,连接PO,则PO⊥平面
ABCD,易知BO=,所以PO=
=,所以正四棱台ABCD-A1B1C1D1
的高为,所以=×
(22+12+)×=.(或者V四棱锥P-ABCD=×22×=,
=V四棱锥P-ABCD,所以=
V四棱锥P-ABCD-=V四棱锥P-ABCD==.)]
名师点评 求空间几何体的体积的常用方法
公式法 规则几何体的体积问题,直接利用公式进行求解
割补法 把不规则的几何体分割成规则的几何体,或者补成规则的几何体,再求解
等体 积法 通过选择合适的底面来求几何体的体积,特别是三棱锥的体积(即利用三棱锥的任一个面均可作为三棱锥的底面,进行等体积变换)
[跟进训练]
2.(1)(2024·山东枣庄一模)已知圆台的上、下底面半径分别为1和3,侧面展开图是半个圆环,则圆台的侧面积为( )
A.6π B.16π
C.26π D.32π
√
(2)(2024·北京西城二模)楔体形构件在建筑工程上有广泛的应用.如图,某楔体形构件可视为一个五面体ABCDEF,其中平面ABCD为正方形.若AB=6 cm,EF=3 cm,且EF与平面ABCD的距离为2 cm,则该楔体形构件的体积为( )
A.18 cm3 B.24 cm3
C.30 cm3 D.48 cm3
(3)(2020·新高考Ⅱ卷)棱长为2的正方体ABCD-A1B1C1D1中,M,N分别为棱BB1,AB的中点,则三棱锥A1-D1MN的体积为________.
√
1
(1)B (2)C (3)1 [(1)圆台的上底面圆半径r′=1,下底面圆半径r=3,
设圆台的母线长为l,扇环所在的小圆的半径为x,依题意有解得所以圆台的侧面积S=πl=π×4=16π.故选B.
(2)如图所示,设G,H分别为AB,DC的中点,连接EG,EH,GH,
因为底面ABCD为正方形,所以AB∥DC,又AB 平面EFCD,DC 平面EFCD,所以AB∥平面EFCD,
又平面EFCD∩平面ABFE=EF,所以AB∥EF,
因为G,H分别为AB,DC的中点,AB=6 cm,EF=3 cm,
所以EF∥GB,EF=GB,则四边形EGBF为平行四边形,则EG∥FB,
同理EH∥FC,又GH∥BC,所以EGH-FBC为三棱柱,由题意,可得V四棱锥E-AGHD=S矩形AGHD·h=AD·AG·h=×6×3×2=12(cm3).
又V三棱柱EGH-FBC=3V三棱锥B-EGH=3V三棱锥E-BGH=3××V四棱锥E-AGHD=·V四棱锥E-AGHD=×12=18(cm3).
所以该多面体的体积为V=V四棱锥E-AGHD+V三棱柱EGH-FBC=12+18=30(cm3).故选C.
(3)如图,易知=,由正方体的结构特征,知D1A1⊥平面A1MN,所以D1A1为三棱锥D1-A1MN的高.因为M,N分别为棱BB1,AB的中点,所以=2×2-×1×1-×1×2-×1×2=,所以==××D1A1=×2=1.]
【教用·备选题】
1.(2024·辽宁大连一模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知底面圆的直径AB=12 cm,圆柱体部分的高BC=6 cm,圆锥体部分的高CD=4 cm,则这个陀螺的表面积(单位:cm2)为
( )
A.π B.π
C.π D.π
√
C [由题意可知,圆锥的母线长为=2,
所以这个陀螺的表面积为π×62+2π×6×6+π×2×6=π.
故选C.]
2.《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”意思为:今有底面为矩形的屋脊形状的多面体(如图),下底面宽AD=3丈,长AB=4丈,上棱EF=2丈,EF与平面ABCD平行,EF与平面ABCD的距离为1丈,则它的体积是( )
A.4立方丈 B.5立方丈
C.6立方丈 D.8立方丈
√
B [如图,过点E作EG⊥平面ABCD,垂足为点G,过点F作FH⊥平面ABCD,垂足为点H,过点G作PQ∥AD,交AB于点Q,交CD于点P,过点H作MN∥BC,交AB于点N,交CD于点M,连接EQ,EP,FN,FM.则AQ+NB=4-2=2,QN=2,且四边形AQPD与四边形NBCM都是矩形.
则它的体积V=VE-AQPD+VEPQ-FMN+VF-NBCM=·EG·S矩形AQPD+S△EPQ·NQ+·FH·S矩形NBCM=(AQ+NB)·AD·EG+S△EPQ·NQ=×2×3×1+×3×1×2=5(立方丈).]
3.(2024·江苏常州模拟)如图,圆锥的底面半径为1,侧面展开图是圆心角为60°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为,则圆台的侧面积为
( )
A. B.
C. D.8π
√
C [设圆锥的半径为R,母线长为l,则R=1.设圆台的上底面半径为r,母线长为l1,则r=.
由已知可得,==,所以l=6.
如图,作出圆锥、圆台的轴截面,
则有==,所以l1=4.
所以圆台的侧面积为π(R+r)l1=4×π=π.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
一、单项选择题
1.(2025·陕西西安模拟)乒乓球被誉为我国的“国球”,一个标准尺寸乒乓球的直径是40 mm,则其表面积约为( )
A.3 000 mm2 B.4 000 mm2
C.5 000 mm2 D.6 000 mm2
13
课后作业(三十八) 基本立体图形、简单几何体的表面积与体积
√
14
C [标准尺寸乒乓球的直径是40 mm,标准乒乓球的半径R=20 mm,故表面积S=4πR2≈5 000 mm2.故选C. ]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
2.(2024·广西来宾一模)已知一个正四棱台的上、下底面边长分别为1,2,体积为3,则该正四棱台的高为( )
A.1 B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
D [设该正四棱台的高为h,
又其上、下底面边长分别为1,2,体积为3,
则V=h(12+22+)==3,
所以h=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
3.水平放置的四边形ABCD的直观图是直角梯形A′B′C′D′,如图所示.其中B′C′=A′B′=1,则原平面图形的面积为( )
A. B.
C.3 D.6
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
C [在直角梯形A′B′C′D′中,B′C′=A′B′=1,且∠A′D′C′=45°,作A′P⊥D′C′于点P,
则四边形A′B′C′P为正方形,△A′PD′为等腰直角三角形,
故A′D′=,D′C′=2.
故原图形为直角梯形,且上底AB=A′B′=1,高AD=2A′D′=2,下底DC=D′C′=2.
其面积为×2=3.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
4.(2024·山西晋城二模)已知圆锥的侧面积为12π,它的侧面展开图是圆心角为的扇形,则此圆锥的体积为( )
A.6π B.
C.6π D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
B [设圆锥的底面半径为r,母线长为l,
由题意可得解得l=6,r=2,
则圆锥的高h==4,
所以此圆锥的体积为h×πr2=.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
5.将12根长度相同的小木棍通过黏合端点的方式拼接(不可折断,可以不全部用完),不可能拼成( )
A.正三棱柱 B.正四棱锥
C.正四棱柱 D.正六棱锥
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
D [正三棱柱中9条棱的长度可以相等,A成立;
正四棱锥中8条棱的长度可以相等,B成立;
正四棱柱中12条棱的长度可以相等,C成立;
因为正六边形的中心到六个顶点的距离都等于边长,
所以正六棱锥的侧棱总比底边长,D不成立.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
6.(2023·天津高考)在三棱锥P-ABC中,线段PC上的点M满足PM=PC,线段PB上的点N满足PN=PB,则三棱锥P-AMN和三棱锥P-ABC的体积之比为( )
A. B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
B [如图,因为PM=PC,PN=PB,所以====,所以====(其中d为点A到平面PBC的距离,因为平面PMN和平面PBC重合,所以点A到平面PMN的距离也为d).
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
二、多项选择题
7.如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,将容器以BC为轴顺时针旋转,则( )
A.有水的部分始终是棱柱
B.水面所在四边形EFGH为矩形且面积不变
C.棱A1D1始终与水面平行
D.当点H在棱CD上且点G在棱CC1上(均不含端点)时,
BE·BF不是定值
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
AC [对于A,有水的部分的几何体,有两个面都垂直于BC,这两个面始终平行,而AD∥BC,
并且BC始终与水面平行,即有FG∥BC,若点H在棱DD1上,由面面平行的性质知,
EH∥FG,若点H在棱CD上,EH∥BC,因此该几何体有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边互相平行,即该几何体是棱柱,A正确;
对于B,因为水面EFGH为矩形,边FG的长度不变,EF随旋转角的变化而变化,矩形EFGH的面积不是定值,B错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于C,因为A1D1始终与BC平行,而BC始终与水面平行,并且A1D1不在水面所在平面内,即棱A1D1始终与水面平行,C正确;
对于D,当点H在棱CD上且点G在棱CC1上(均不含端点)时,有水部分的棱柱的底面为三角形,
而水的体积不变,高BC不变,则底面面积BE·BF不变,即BE·BF为定值,D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
8.(2024·江苏徐州一模)已知圆台的上、下底面直径分别为2,6,高为2,则( )
A.该圆台的体积为26π
B.该圆台外接球的表面积为π
C.用过任意两条母线的平面截该圆台所得截面周长的最大值为16
D.挖去以该圆台上底面为底,高为的圆柱后所得几何体的表面积为π
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
BC [由已知得圆台的上、下底面半径分别为1,3,
对于A,圆台的体积为π×2=π,A错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于B,如图是圆台的轴截面ABCD,外接球球心为O,设外接球半径为R,
当球心在梯形ABCD内时,=2,解得R2=,
当球心在梯形ABCD外时(图略),=2,方程无解,
所以外接球的表面积为4πR2=π,B正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于C,用过任意两条母线的平面截该圆台所得截面中,轴截面的周长最大,
又母线长为=4,则最大周长为4+4+2+6=16,C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
对于D,如图,挖去以该圆台上底面为底,高为的圆柱后所得几何体的表面积为
π×4+2π×1×+π×=26π+2π,D错误.
故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
三、填空题
9.如图,四边形OABC是边长为1的正方形,是四分之一圆,则图中阴影部分以OC所在直线为旋转轴旋转一周得到的旋转体的表面积为________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
5π
5π [该旋转体是一个圆柱挖去一个半球后剩余的部分,且圆柱的底面半径是1,高是1,球的半径是1,所以该旋转体的表面积为π×12+2π×1×1+×4π×12=5π.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
10.(人教A版必修第二册P116练习T3改编)某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的(如图),则该几何体共有_____个面;若被截正方体的棱长是60 cm,那么该石凳的表面积是_________________cm2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
14
10 800+3 600
14 10 800+3 600 [由题意知,截去的八个四面体是全等的正三棱锥,石凳的8个面为三角形,6个面为正方形,所以该几何体共有14个面;
如果被截正方体的棱长是60 cm,那么石凳的表面积是
S=8××30×30×sin 60°+6×30×30=.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
11.(2025·陕西安康模拟)随着古代瓷器工艺的高速发展,在著名的宋代五大名窑之后,又增加了三种瓷器,与五大名窑并称为中国八大名瓷,其中最受欢迎的是景德镇窑.如图,景德镇产的青花玲珑瓷(无盖)的形状可视为一个球被两个平行平面所截后剩下的部分,其中球面被平面所截的部分均可视为球冠(截得的圆面是底,垂直于圆面的直径被截得的部分是高,其面积公式为S=2πRh,其中R为球的半径,h为球冠的高).已知瓷器的高为38 cm,在高为20 cm处有最大直径(外径)为48 cm,则该瓷器的外表面积约为(π取3.14) ( )
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
A.6 270 cm2
B.6 275 cm2
C.6 280 cm2
D.6 300 cm2
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
C [由题意可知,球的半径为R=24 cm,上球冠的高h1=6 cm,下球冠的高h2=4 cm,
设下底面圆的半径为r,则r2=242-202=176,
所以该瓷器的外表面积为4π×242-2π×24×6-2π×24×4+π×176=
2 000π≈6 280.
故选C.]
12.(2025·陕西西安模拟)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商准备将棱长为8 cm的正四面体的魔方放入正方体盲盒内,为节约成本,使得魔方能够放入盲盒且盲盒棱长最小,则盲盒内剩余空间的体积为( )
A. cm3 B. cm3
C. cm3 D. cm3
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
C [依题意,要将棱长为8 cm的正四面体的魔方放入正方体盲盒内,且盲盒棱长最小,则当且仅当正方体的面对角线长等于正四面体的棱长,即它们有相同的外接球,
如图,正四面体ABCD的棱长为8 cm,
所以该正方体的棱长为4 cm,盲盒内剩余空间
的体积为4××4×4×4=(cm3).故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
13.(多选)(2022·新高考Ⅱ卷)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则( )
A.V3=2V2
B.V3=V1
C.V3=V1+V2
D.2V3=3V1
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
√
√
CD [设AB=ED=2FB=2,则V1=×2×2×2=,V2=×2×2×1=.连接BD交AC于点M,连接EM,FM(图略),则FM=,EM=,EF=3,则FM2+EM2=EF2,故S△EMF==,V3=×AC=2,V3=V1+V2,2V3=3V1,故选CD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
14.(2024·九省联考)已知轴截面为正三角形的圆锥的高与球O的直径相等,则圆锥的体积与球O的体积的比值是________,圆锥的表面积与球O的表面积的比值是________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
1 [设圆锥的底面半径为r,球的半径为R,
因为圆锥的轴截面为正三角形,所以圆锥的高h=r,母线长l=2r,由题可知,h=2R,所以球的半径R=r,
1
所以圆锥的体积为V1=×π×r2×r=πr3,
球的体积V2=πR3=π×=πr3,
所以==.
圆锥的表面积S1=πrl+πr2=3πr2,
球的表面积S2=4πR2=4π×=3πr2,
所以==1.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
谢 谢!
同课章节目录
