五下人教版数学【组合图形体积和表面积专训】(含答案)
文档属性
| 名称 | 五下人教版数学【组合图形体积和表面积专训】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 13:31:16 | ||
图片预览

文档简介
五年级下册组合图形体积和表面积专训
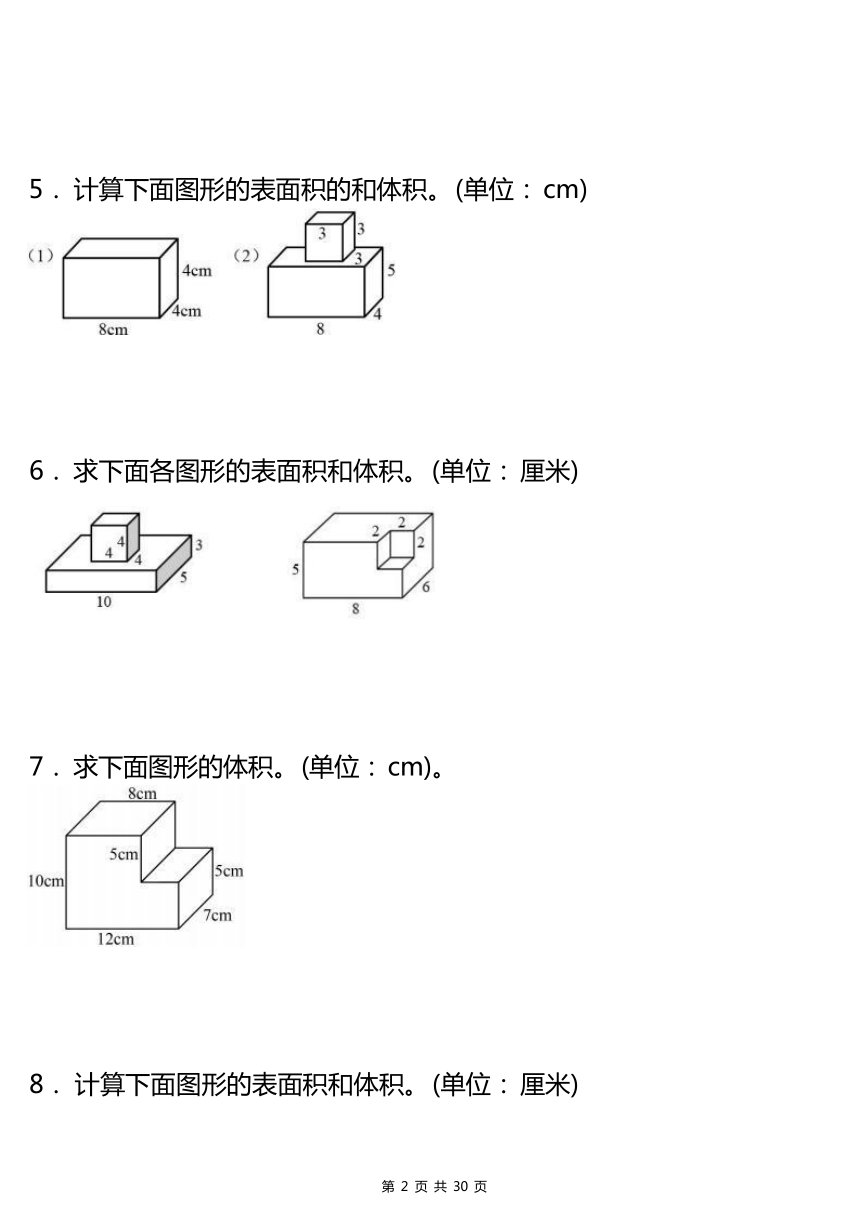
1. 下图中长方体长 8 厘米 、宽 6 厘米 、高 4 厘米, 正方体的棱长是5 厘米。 请计算组合体的表面积和体积。
2. 计算下面立体图形的表面积和体积。
3. 求出下面组合图形的表面积和体积(单位: cm)。
4. 计算如图物体的表面积和体积。 (单位: 分米)
第 1 页 共 30 页
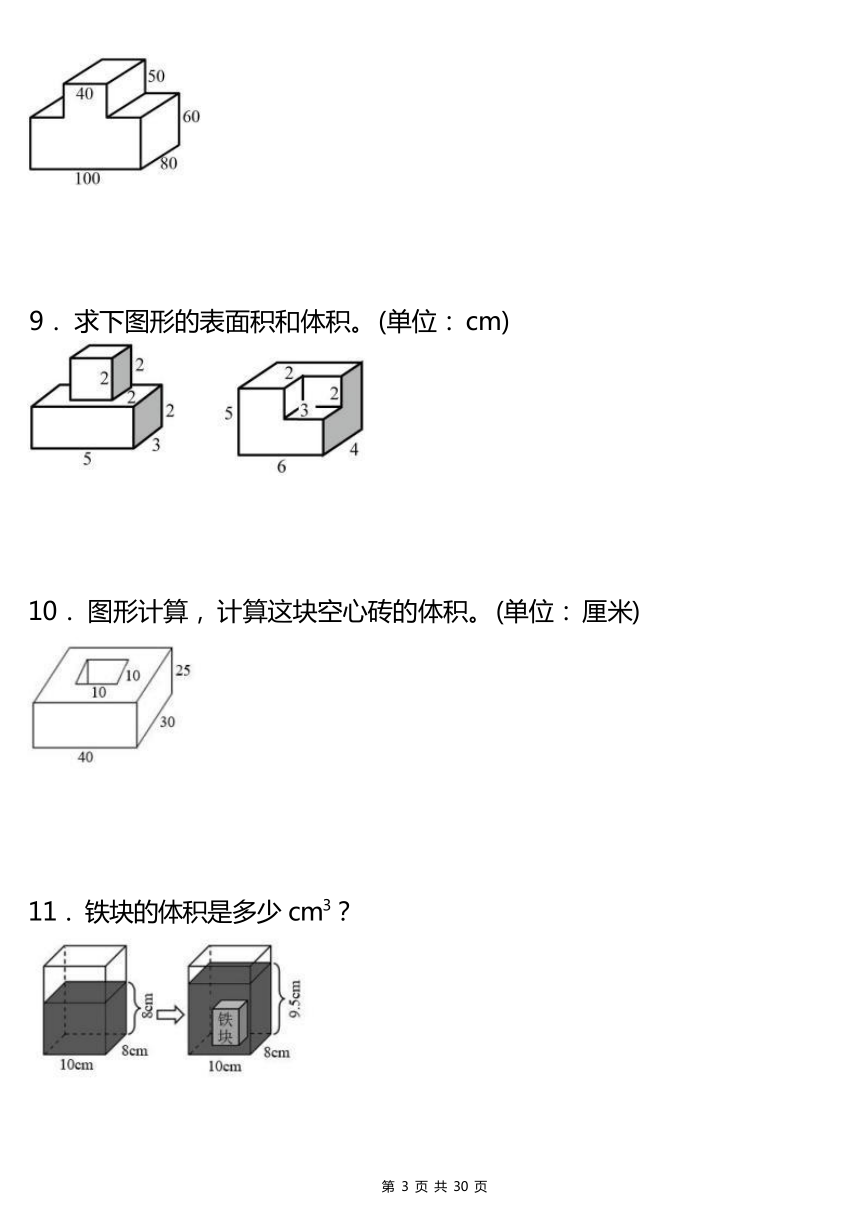
5. 计算下面图形的表面积的和体积。 (单位: cm)
6. 求下面各图形的表面积和体积。 (单位: 厘米)
7. 求下面图形的体积。 (单位: cm)。
8. 计算下面图形的表面积和体积。 (单位: 厘米)
第 2 页 共 30 页
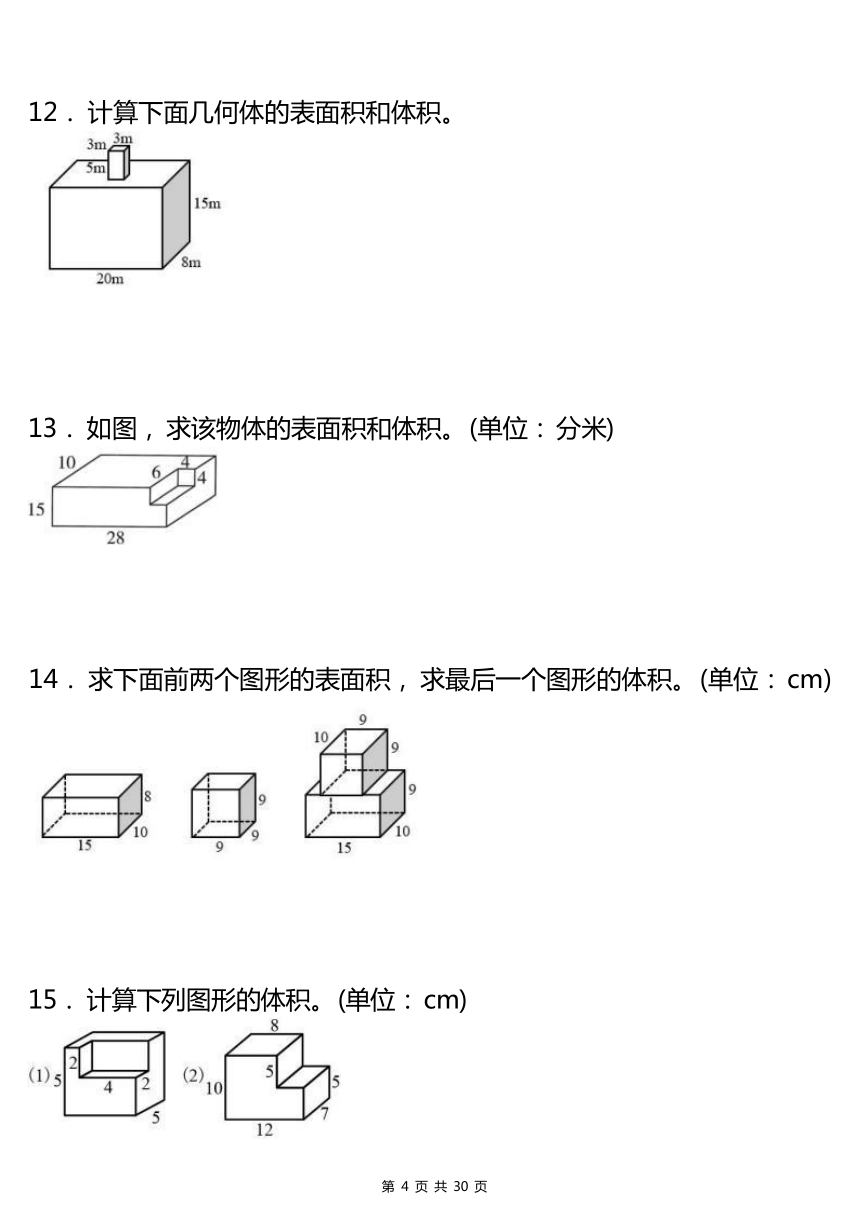
9. 求下图形的表面积和体积。 (单位: cm)
10. 图形计算, 计算这块空心砖的体积。 (单位: 厘米)
11. 铁块的体积是多少 cm3?
第 3 页 共 30 页
12. 计算下面几何体的表面积和体积。
13. 如图, 求该物体的表面积和体积。 (单位: 分米)
14. 求下面前两个图形的表面积, 求最后一个图形的体积。 (单位: cm)
15. 计算下列图形的体积。 (单位: cm)
第 4 页 共 30 页
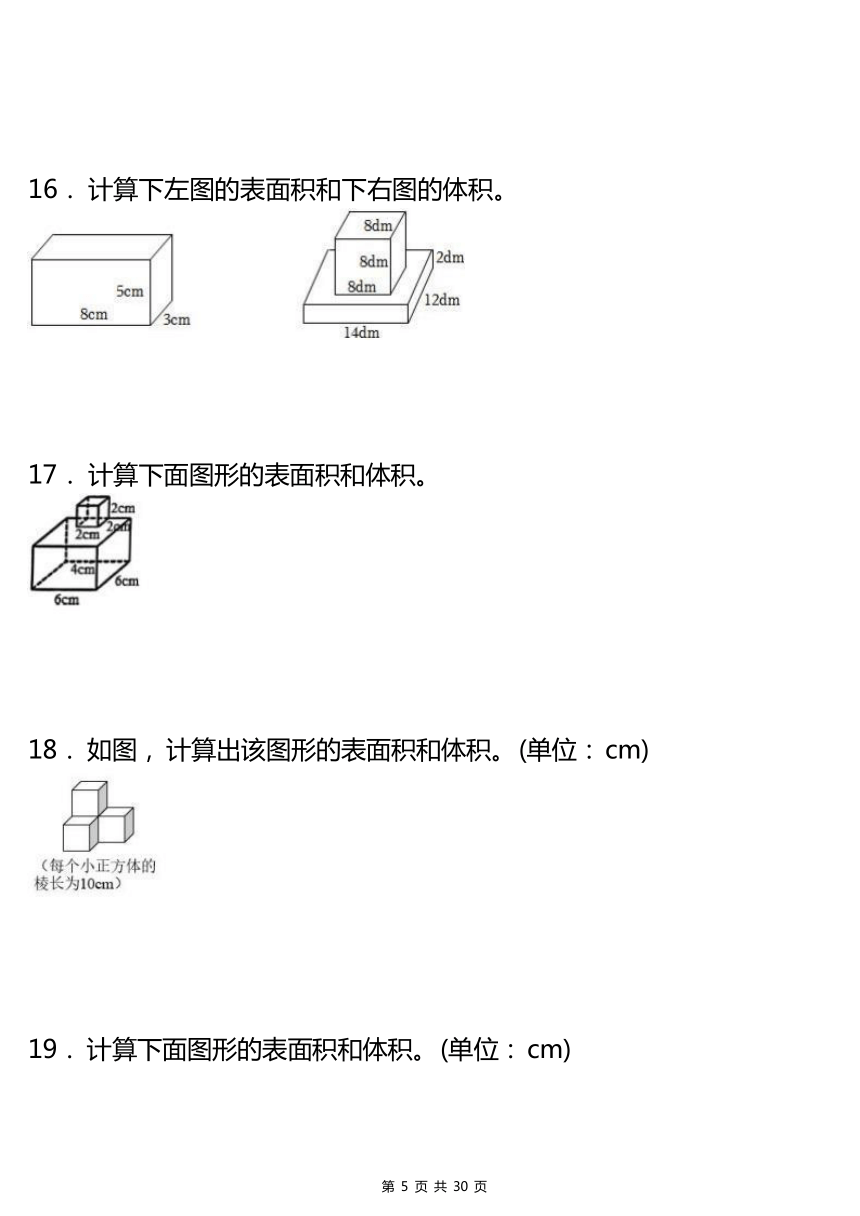
16. 计算下左图的表面积和下右图的体积。
17. 计算下面图形的表面积和体积。
18. 如图, 计算出该图形的表面积和体积。 (单位: cm)
19. 计算下面图形的表面积和体积。 (单位: cm)
第 5 页 共 30 页
20. 求下列立体图形的表面积与体积。
(1) (2)
第 6 页 共 30 页
专题1 长方体和正方体(组合体的体积和表面积配套训练)
(答案解析)
1 .308 平方厘米 ;317 立方厘米
【 分析】组合体的表面积=完整的长方体表面积+正方体4 个面的面积和 ,长方体表面积=(长×宽+长×高+宽×高)×2 ; 组合体的体积=长方体体积+正方体体积 ,长方体体积=长 ×宽×高 ,正方体体积=棱长×棱长×棱长 ,据此列式计算 。 【详解 】(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100 = 104×2+100
= 208+100
=308(平方厘米) 8×6×4+5×5×5
= 192+125
=317(立方厘米)
2 .表面积:23m2 ;体积:6m3
【 分析】观察图形可知 ,该立体图形的表面积等于下方长 方体的表面积加上上方长方体的侧面积 ,根据长方体的表 面积公式:S=(ab+a h+bh)×2 ,长方体的侧面积公式:S=Ch , 据此进行计算即可; 该立体图形的体积等于下方长方体的 体积加上上方长方体的体积 ,再根据长方体的体积公式:V = abh ,据此进行计算即可 。
第 7 页 共 30 页
【详解 】表面积:(3×1.5+3×1+1.5×1)×2+(1.5+1)×2×1 =(4.5+3+1.5)×2+2.5×2×1
= 9×2+5×1 = 18+5
=23(m2)
体积:3×1.5×1+1×1×1.5
= 4.5×1+1×1.5 = 4.5+1.5
=6(m3)
3 .表面积 428cm2 ;体积 365cm3
【 分析】观察图形可知 ,正方体与长方体有重合的部分 , 把正方体的上面向下平移 ,补给长方体的上面; 这样长方 体的表面积是6 个面的面积之和 ,而正方体只需计算 4 个 面(前后面和左右面)的面积;
组合图形的表面积=长方体的表面积+正方体 4 个面的面积 , 根据长方体的表面积=(长×宽+长×高+宽×高)×2 ,正方体4 个面的面积=棱长×棱长×4 ,代入数据计算 ,即可求出这个 组合图形的表面积 。
组合图形的体积=长方体的体积+正方体的体积 ,根据长方 体的体积=长×宽×高 ,正方体的体积=棱长×棱长×棱长 , 代入数据计算 ,即可求出这个组合图形的体积 。
【详解 】表面积:
(12×10+12×2+10×2)×2+5×5×4 =(120+24+20)×2+5×5×4
= 164×2+25×4
= 328+100
第 8 页 共 30 页
=428(cm2) 体积:
12×10×2+5×5×5 = 240+125
=365(cm3)
组合图形的表面积是428cm2 ,组合图形的体积是 365cm3 。 4 .150 平方分米 ;109 立方分米
【 分析】根据正方体的体积 、表面积的意义 ,从正方体的 顶点上挖掉一个小长方体 ,因为这个小长方体原来外露3 个面 ,挖掉这个小长方体后又外露与原来相同的3 个面 , 所以剩下图形的表面积不变 ,体积减少了一个小长方体的 而体积 ,据此解答即可 。
【详解 】5×5×6 = 25×6
=150(平方分米) 5×5×5-4×2×2
= 125-16
= 109(立方分米)
5 .(1)160cm2 ;128cm3
(2)220cm2 ;187cm3
【 分析 】(1)长方体的表面积=(长×宽+长×高+宽×高)×2 ,长 方体的体积=长×宽×高 ,把长方体的长 13 厘米 、宽 4 厘米 、 高 5 厘米的值分别代入长方体的表面积公式 、体积公式计 算即可 。
(2)通过观察图形可知 ,因为正方体和长方体粘合在一起 , 所以在求表面积时上面的正方体只求它的 4 个侧面的面积 ,
第 9 页 共 30 页
下面的长方体求出表面积 ,然后合并即可; 这个组合图形 的体积等于长方体的体积加上正方体的体积 。根据正方体 的表面积公式:S=6a2 ,体积公式:V=a3 ,长方体的表面 积公式:S=(ab+a h+bh)×2 ,体积公式:V=abh ,把数据代 入公式解答 。
【详解 】(1)(8×4+8×4+4×4)×2 =(32+32+16)×2
= 80×2
= 160(cm2) 8×4×4
= 32×4
= 128(cm3)
长方体的表面积是 160cm2 ,体积是 128cm3 。
(2)(8×4+8×5+4×5)×2+3×3×4
=(32+40+20)×2+9×4 = 92×2+36
= 184+36
=220(cm2) 8×4×5+3×3×3 = 32×5+9×3 = 160+27
= 187(cm3)
组合图形的表面积是 220cm2 ,体积是 187cm3 。
6 .左图表面积是 254 平方厘米 ,体积是 214 立方厘米 ;右 图表面积是236 平方厘米 ,体积是232 立方厘米 。
【 分析】 通过观察图形可知 ,由于上面的正方体和下面的
第 10 页 共 30 页
长方体粘合在一起 ,所以上面的正方体只求它的4 个侧面 的面积 ,下面的长方体求它的表面积 ,然后合并起来即可 , 根据正方体的表面积公式:S=6a2 ,长方体的表面积公式: S=(ab+a h+bh)×2 ,把数据代入公式求出它的表面积 ,根据 正方体的体积公式:V=a3 ,长方体的体积公式:V=abh , 把数据代入公式求出它的体积 。
大长方体挖去一个小正方体 ,凹下去图形的三个面的面积 刚好能补上原来缺失的三个面的面积 ,所以大长方体的表 面积没有改变 。用长方体的表面积公式求解即可 。组合体 的体积用大长方体的体积减去小正方体的体积即可 。
【详解 】
4x4x4+(10x5+10x3+5x3)x2 =16x4+(50+30+15)x2
=64+95x2
=64+190
=254(平方厘米) 4x4x4+10x5x3 =16x4+50x3
=64+150
=214(立方厘米)
它的表面积是254 平方厘米 ,体积是 214 立方厘米 。
(8x6+8x5+6x5)x2 =(48+40+30)x2
=118x2
= 236(平方厘米) 8x6x5-2x2x2
第 11 页 共 30 页
=48x5-4x2
=240-8
=232(立方厘米)
它的表面积是236 平方厘米 ,体积是 232 立方厘米 。 7 .700cm3
【 分析】如图 ,将组合体分成两个长方体, 长方体体积=长×宽×高 ,据此分别求出两个长方体体积 , 相加即可 。
【详解 】 12-8=4(cm) 8×7×10+4×7×5
= 560+140 =700(cm3)
8 .表面积为:49600 平方厘米 ;体积为:640000 立方厘米 【 分析】 图中组合图形的表面积等于长为 100 厘米 ,宽为
80 厘米 ,高为(60+50)厘米的长方体的表面积减去 4 个长为
50 厘米 ,宽为(100-40)÷2 厘米的长方形的面积 ,分别利用 长方体的表面积和长方形的面积公式 ,再相减即可求出组 合图形的表面积;
图中的组合图形的体积等于长为 100 厘米 ,宽为80 厘米 , 高为(60+50)厘米的长方体的体积减去 2 个长为(100-40)÷2 厘米 ,宽为80 厘米 ,高为50 厘米的长方体的体积 ,利用 长方体的体积公式 ,再相减即可求出组合图形的体积 。
【详解 】(100-40)÷2 = 60÷2
第 12 页 共 30 页
=30(厘米)
100×80×2+100×(60+50)×2+80×(60+50)×2-4×50×30 = 16000+100×110×2+80×110×2-6000
= 16000+22000+17600-6000
=49600(平方厘米)
100×80×(60+50)-2×30×80×50 = 100×80×110-4800×50
= 880000-240000
=640000(立方厘米)
即图形的表面积是49600 平方厘米 ,体积是 640000 立方厘 米 。
9 .78cm2 ;38cm3 ; 148cm2 ;108cm3
【 分析】观察图形一可知 ,该图形的体积等于长方体的体 积加上正方体的体积 ,根据长方体的体积公式:V=abh , 正方体的体积公式:V=a3 ,据此代入数值进行计算即可; 该图形的表面积等于长方体的表面积加上正方体的表面积 , 再减去正方体两个面的面积 ,再结合长方体的表面积公式: S=(ab+a h+bh)×2 ,正方体的表面积公式:S=a2×6 ,据此进 行计算即可; 观察图形二可知 ,该长方体的顶点处少了一 个小长方体 ,该图形的表面积与完整图形的表面积相等 , 根据长方体的表面积:S=(ab+a h+bh)×2 ,据此求出该图形 表面积即可; 该图形的长方体的体积等于大长方体的体积 减去小长方体的体积 ,再根据长方体的体积:V=abh ,据 此计算即可 。
【详解 】 图一表面积:(5×3+5×2+3×2)×2+2×2×6-2×2×2
第 13 页 共 30 页
=(15+10+6)×2+4×6-8
= 31×2+24-8
= 62+24-8
= 86-8
=78(cm2)
图一体积:5×3×2+2×2×2 = 15×2+4×2
= 30+8
=38(cm3)
图二表面积:(6×4+6×5+5×4)×2
=(24+30+20)×2 = 74×2
= 148(cm2)
图二体积:6×5×4-3×2×2 = 30×4-6×2
= 120-12
= 108(cm3)
10 .27500 立方厘米
【 分析】 长方体体积=长×宽×高 。空心砖的体积用大方体 的体积减去小长方体的体积即可 。
【详解 】40×30×25-10×10×25 = 1200×25-100×25
= 30000-2500
=27500(立方厘米) 11 .120cm3
【 分析】 水面上升的体积就是铁块的体积 ,长方体容器的
第 14 页 共 30 页
长×宽×上升的水的高度=铁块体积 ,据此列式计算 。 【详解 】 10×8×(9.5-8)
= 80×1.5
= 120(cm3)
12 .1220m2 ;2445m3
【 分析 】长方体的表面积=(长×宽+宽×高+长×高)×2 ,长方 体的体积=长×宽×高 ,几何体的表面积=大长方体的表面 积+小长方体 4 个侧面的面积 ,几何体的体积=大长方体的 体积+小长方体的体积 ,据此解答 。
【详解 】表面积:(20×8+20×15+8×15)×2+5×3×4 =(160+300+120)×2+5×3×4
= 580×2+5×3×4 = 1160+60
= 1220(m2)
体积:20×8×15+5×3×3 = 160×15+15×3
= 2400+45 =2445(m3)
所以 ,这个几何体的表面积是 1220m2 ,体积是 2445m3 。
13 .表面积是 1700 平方分米 ,体积是4104 立方分米
【 分析】 通过观察这个物体的三视图发现 ,一个长方体的 一个角被挖去一个小长方体 ,表面积没有发生变化 ,体积 减少 ,所以直接根据长方体的表面积公式: 长方体的表面 积=(长×宽+长×高+宽×高)×2 即可求出这个物体的表面积 , 然后根据长方体体积公式: 长方体的体积=长×宽×高 ,用 28×15×10-4×4×6 即可求出这个物体的体积 。据此解答 。
第 15 页 共 30 页
【详解 】表面积:(28×10+28×15+15×10)×2
=(280+420+150)×2
= 850×2
=1700(平方分米)
体积:28×15×10-4×4×6 = 4200-96
=4104(立方分米)
该物体的表面积是 1700 平方分米 ,体积是 4104 立方分米 。 14 .700cm2 ;486cm2 ;2160cm3
【 分析 】根据长方体的表面积公式:S=(ab+a h+bh)×2 ,正 方体的表面积公式:S=6a2 ,据此代入数值即可求解; 最 后一个图形的体积等于下面的长方体的体积加上上面长方 体的体积 ,根据长方体的体积公式:V=abh ,据此进行计 算即可 。
【详解 】(15×10+15×8+10×8)×2 =(150+120+80)×2
= 350×2
=700(cm2) 9×9×6
= 81×6
=486(cm2)
15×10×9+10×9×9 = 150×9+90×9 = 1350+810
=2160(cm3)
15 .(1)109cm3
第 16 页 共 30 页
(2)700cm3
【 分析】(1)由图可知 ,图形是正方体中挖空了一个长方体 , 图形的体积=正方体的体积-长方体的体积; 正方体的体积 =棱长×棱长×棱长 ,长方体的体积=长×宽×高;
(2)图形是由长为 12cm ,宽为 7cm ,高为 10cm 的长方体中 , 挖空了一个长为 7cm ,宽为(12-8)cm ,高为 5cm 的小长方体 , 根据公式: 长方体的体积=长×宽×高 ,分别计算出这两个 长方体的体积 ,再相减即可; 据此解答 。
【详解 】(1)5×5×5-4×2×2 = 25×5-8×2
= 125-16
= 109(cm3)
(2)12×7×10-(12-8)×7×5 = 84×10-4×7×5
= 840-28×5 = 840-140 =700(cm3)
16 .158cm2 ;848dm3
【 分析】根据长方体表面积公式: 长方体的表面积=(长× 宽+长×高+宽×高)×2 ,用(8×3+8×5+3×5)×2 即可求出左图长方 体的表面积;
右图由一个棱长为8dm 的正方体和一个长为 14dm 、宽为 12dm 、高为2dm 的长方体组成 ,根据长方体的体积=长× 宽×高和正方体的体积=棱长×棱长×棱长 ,用 14×12×2+8×8× 8 即可求出右图的体积 。
第 17 页 共 30 页
【详解 】(8×3+8×5+3×5)×2
=(24+40+15)×2 = 79×2
= 158cm2
左图的长方体表面积是 158cm2 。
14×12×2+8×8×8 = 336+512
= 848dm3
右图的体积是 848dm3 。
17 .184 平方厘米 ;152 立方厘米
【 分析】观察图形可知 ,该图形的表面积等于长方体的表 面积加上正方体的4 个面的面积 ,根据长方体的表面积公 式:S=(ab+a h+bh)×2 ,正方形的面积公式:S=a2 ,据此进 行计算即可; 该图形的体积等于长方体的体积加上正方体 的体积 ,根据长方体的体积公式:V=abh ,正方体的体积 公式:V=a3 ,据此进行计算即可 。
【详解 】(6×6+6×4+6×4)×2+2×2×4
= 84×2+16
= 168+16
= 184(平方厘米) 6×6×4+2×2×2
= 144+8
= 152(立方厘米)
18 .1800cm2 ;4000cm3
【 分析】 看图 ,一共有 4 个小正方体 ,并且一共有6 个面 被遮盖住了 ,所以只要求 18 个面的面积和 。用棱长×棱长×
第 18 页 共 30 页
18 ,即可求出该图形的表面积;
正方体体积=棱长×棱长×棱长 ,据此先求出 1 个小正方体 的体积 ,再将其乘4 ,求出该图形的体积 。
【详解 】表面积 :10×10×18= 1800(cm2) 体积 :10×10×10×4=4000(cm3)
19 .表面积 384cm2 ;体积 497cm3
【 分析】从图中可知 ,在图形右上方的顶点处挖掉了一个 小长方体 ,露出了3 个面 ,这 3 个面可以向外平移 ,正好 补齐缺口 ,补成一个完整的正方体 ,所以图形的表面积 = 正方体的表面积 ,根据正方体的表面积=棱长×棱长×6 ,代 入数据计算求解 。
图形的体积=正方体的体积-挖掉的小长方体的体积 ,根据 正方体的体积=棱长×棱长×棱长 ,长方体的体积=长×宽× 高 ,代入数据计算求解 。
【详解 】表面积:
8×8×6
= 64×6
=384(cm2) 体积:
8×8×8-2×2.5×3 = 64×8-5×3
= 512-15
=497(cm3)
图形的表面积是 384cm2 ,体积是 497cm3 。
20 .(1)324cm2 ;360cm3
(2)30m2 ;6m3
第 19 页 共 30 页
【 分析 】(1)根据长方体表面积公式 S=(ab+a h+bh)×2 ,体积 公式 V=abh ,代入数据计算求解 。
(2)组合图形的表面积=正方体表面积-长方体上下面的面 积+长方体的侧面积 ,其中长方体上下面是2 个边长为 1m 的正方形 ,长方体的侧面是 4 个相同的长为2m 、宽为 1m 的长方形; 根据正方体的表面积公式 S=6a2 ,正方形的面 积公式 S=a2 ,长方形的面积公式 S=ab ;代入数据计算求 解 ;
组合图形的体积= 正方体的体积-长方体的体积; 根据正方 体的体积公式 V=a3 ,长方体的体积公式 V=abh ,代入数 据计算求解 。
【详解 】(1)表面积:
(12×6+12×5+6×5)×2 =(72+60+30)×2
= 162×2
=324(cm2)
体积:
12×6×5=360(cm3)
长方体的表面积是 324cm2 ,体积是 360cm3 。
(2)表面积:
2×2×6-1×1×2+2×1×4 = 24-2+8
=30(m2)
体积:
2×2×2-1×1×2 = 8-2
第 20 页 共 30 页
=6(m3)
组合图形的表面积是 30m2 ,体积是 6m3 。
五年级数学下册长方体和正方体专训
(
组合图形体积和表面积
)
第 21 页 共 30 页
1. 下图中长方体长 8 厘米 、宽 6 厘米 、高 4 厘米, 正方体的棱长是5 厘米。 请计算组合体的表面积和体积。
(8×6+8×4+6×4)×2+5×5×4 = (48+32+24) ×2+100 = 104×2+100
= 208+ 100
= 308(平方厘米 )
8×6×4+5×5×5
= 192+125
=317(立方厘米)
2. 计算下面立体图形的表面积和体积。
表面积:
(3×1.5+3×1+1.5×1)×2+(1.5+1)×2×1 =(4.5+3+1.5)×2+2.5×2×1
= 9×2+5×1 = 18+5
=23(m2)
体积:3×1.5×1+1×1×1.5
= 4.5×1+1×1.5 = 4.5+1.5
=6(m3)
3. 求出下面组合图形的表面积和体积(单位: cm )。
表面积:
(12×10+12×2+10×2)×2+5×5×4 =(120+24+20)×2+5×5×4
= 164×2+25×4 = 328+100
第 22 页 共 30 页
=428(cm2)
体积:
12×10×2+5×5×5 = 240+125
=365(cm3)
4. 计算如图物体的表面积和体积。(单位: 分米)
5×5×6
= 25×6
=150(平方分米)
5×5×5-4×2×2 = 125-16
= 109(立方分米)
5. 计算下面图形的表面积的和体积。(单位: cm )
(8×4+8×4+4×4)×2 =(32+32+16)×2 = 80×2
= 160(cm2)
8×4×4
= 32×4
= 128(cm3)
(8×4+8×5+4×5)×2+3×3×4
=(32+40+20)×2+9×4 = 92×2+36
= 184+36 =220(cm2)
8×4×5+3×3×3
第 23 页 共 30 页
= 32×5+9×3 = 160+27 = 187(cm3)
6. 求下面各图形的表面积和体积。(单位: 厘米)
4x4x4+(10x5+10x3+5x3)x2 =16x4+(50+30+15)x2
=64+95x2
=64+190
=254(平方厘米)
4x4x4+10x5x3 =16x4+50x3
=64+150
=214(立方厘米)
(8x6+8x5+6x5)x2 =(48+40+30)x2
=118x2
= 236(平方厘米)
8x6x5-2x2x2
=48x5-4x2
=240-8
=232(立方厘米)
7. 求下面图形的体积。(单位: cm )。
12–8=4(cm) 8×7×10+4×7×5 = 560+140
第 24 页 共 30 页
=700(cm3)
8. 计算下面图形的表面积和体积。(单位: 厘米)
(100-40)÷2 = 60÷2
=30(厘米)
100×80×2+100×(60+50)×2+80×(60+50)×2-4×50×30 = 16000+100×110×2+80×110×2-6000
= 16000+22000+17600-6000
=49600(平方厘米)
100×80×(60+50)-2×30×80×50 = 100×80×110-4800×50
= 880000-240000
=640000(立方厘米)
9. 求下图形的表面积和体积。(单位: cm )
图一表面积:
(5×3+5×2+3×2)×2+2×2×6-2×2×2 =(15+10+6)×2+4×6-8
= 31×2+24-8
= 62+24-8
= 86-8
=78(cm2)
体积:5×3×2+2×2×2
= 15×2+4×2 = 30+8
=38(cm3)
图二表面积:
第 25 页 共 30 页
(6×4+6×5+5×4)×2 =(24+30+20)×2 = 74×2
= 148(cm2)
体积:6×5×4=3×2×2 = 30×4-6×2
= 120-12
= 108(cm3)
10. 图形计算, 计算这块空心砖的体积。(单位: 厘米)
40×30×25-10×10×25 = 1200×25-100×25 = 30000-2500
= 27500(立方厘米)
11. 铁块的体积是多少 cm3?
10×8×(9.5-8) = 80×1.5
= 120(cm3)
12. 计算下面几何体的表面积和体积。
表面积:
(
=
580×2+5×3×4
)(20×8+20×15+8×15)×2+5×3×4 =(160+300+120)×2+5×3×4
第 26 页 共 30 页
= 1160+60 = 1220(m2)
体积:20×8×15+5×3×3 = 160×15+15×3
= 2400+45 =2445(m3)
13. 如图, 求该物体的表面积和体积。(单位: 分米)
表面积:
(28×10+28×15+15×10)×2 =(280+420+150)×2
= 850×2
=1700(平方分米)
体积:28×15×10-4×4×6 = 4200-96
=4104(立方分米)
14.求下面前两个图形的表面积,求最后一个图形的体积。(单位:cm )
(15×10+15×8+10×8)×2 =(150+120+80)×2
= 350×2
=700(cm2)
9×9×6 = 81×6
=486(cm2)
15×10×9+10×9×9 = 150×9+90×9 = 1350+810
第 27 页 共 30 页
=2160(cm3)
15. 计算下列图形的体积。(单位: cm )
5×5×5-4×2×2 = 25×5-8×2 = 125-16
= 109(cm3)
12×7×10-(12-8)×7×5 = 84×10-4×7×5
= 840-28×5 = 840-140
=700(cm3)
16. 计算下左图的表面积和下右图的体积。
(8×3+8×5+3×5)×2 =(24+40+15)×2 = 79×2
= 158cm2
14×12×2+8×8×8 = 336+512
= 848dm3
17. 计算下面图形的表面积和体积。
(6×6+6×4+6×4)×2+2×2×4 = 84×2+16
= 168+16
= 184(平方厘米)
6×6×4+2×2×2
= 144+8
= 152(立方厘米)
第 28 页 共 30 页
18. 如图, 计算出该图形的表面积和体积。(单位: cm )
表面积:
10×10×18= 1800(cm2)
体积:
10×10×10×4=4000(cm3)
19. 计算下面图形的表面积和体积。(单位: cm )
表面积:
8×8×6
= 64×6
=384(cm2)
体积:
8×8×8-2×2.5×3 = 64×8-5×3
= 512-15
=497(cm3)
20. 求下列立体图形的表面积与体积。
表面积:
(12×6+12×5+6×5)×2 =(72+60+30)×2
= 162×2
=324(cm2)
体积:
12×6×5=360(cm3)
表面积:
2×2×6-1×1×2+2×1×4
= 24-2+8
第 29 页 共 30 页
=30(m2)
体积:
2×2×2-1×1×2 = 8-2 =6(m3)
第 30 页 共 30 页
1. 下图中长方体长 8 厘米 、宽 6 厘米 、高 4 厘米, 正方体的棱长是5 厘米。 请计算组合体的表面积和体积。
2. 计算下面立体图形的表面积和体积。
3. 求出下面组合图形的表面积和体积(单位: cm)。
4. 计算如图物体的表面积和体积。 (单位: 分米)
第 1 页 共 30 页
5. 计算下面图形的表面积的和体积。 (单位: cm)
6. 求下面各图形的表面积和体积。 (单位: 厘米)
7. 求下面图形的体积。 (单位: cm)。
8. 计算下面图形的表面积和体积。 (单位: 厘米)
第 2 页 共 30 页
9. 求下图形的表面积和体积。 (单位: cm)
10. 图形计算, 计算这块空心砖的体积。 (单位: 厘米)
11. 铁块的体积是多少 cm3?
第 3 页 共 30 页
12. 计算下面几何体的表面积和体积。
13. 如图, 求该物体的表面积和体积。 (单位: 分米)
14. 求下面前两个图形的表面积, 求最后一个图形的体积。 (单位: cm)
15. 计算下列图形的体积。 (单位: cm)
第 4 页 共 30 页
16. 计算下左图的表面积和下右图的体积。
17. 计算下面图形的表面积和体积。
18. 如图, 计算出该图形的表面积和体积。 (单位: cm)
19. 计算下面图形的表面积和体积。 (单位: cm)
第 5 页 共 30 页
20. 求下列立体图形的表面积与体积。
(1) (2)
第 6 页 共 30 页
专题1 长方体和正方体(组合体的体积和表面积配套训练)
(答案解析)
1 .308 平方厘米 ;317 立方厘米
【 分析】组合体的表面积=完整的长方体表面积+正方体4 个面的面积和 ,长方体表面积=(长×宽+长×高+宽×高)×2 ; 组合体的体积=长方体体积+正方体体积 ,长方体体积=长 ×宽×高 ,正方体体积=棱长×棱长×棱长 ,据此列式计算 。 【详解 】(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100 = 104×2+100
= 208+100
=308(平方厘米) 8×6×4+5×5×5
= 192+125
=317(立方厘米)
2 .表面积:23m2 ;体积:6m3
【 分析】观察图形可知 ,该立体图形的表面积等于下方长 方体的表面积加上上方长方体的侧面积 ,根据长方体的表 面积公式:S=(ab+a h+bh)×2 ,长方体的侧面积公式:S=Ch , 据此进行计算即可; 该立体图形的体积等于下方长方体的 体积加上上方长方体的体积 ,再根据长方体的体积公式:V = abh ,据此进行计算即可 。
第 7 页 共 30 页
【详解 】表面积:(3×1.5+3×1+1.5×1)×2+(1.5+1)×2×1 =(4.5+3+1.5)×2+2.5×2×1
= 9×2+5×1 = 18+5
=23(m2)
体积:3×1.5×1+1×1×1.5
= 4.5×1+1×1.5 = 4.5+1.5
=6(m3)
3 .表面积 428cm2 ;体积 365cm3
【 分析】观察图形可知 ,正方体与长方体有重合的部分 , 把正方体的上面向下平移 ,补给长方体的上面; 这样长方 体的表面积是6 个面的面积之和 ,而正方体只需计算 4 个 面(前后面和左右面)的面积;
组合图形的表面积=长方体的表面积+正方体 4 个面的面积 , 根据长方体的表面积=(长×宽+长×高+宽×高)×2 ,正方体4 个面的面积=棱长×棱长×4 ,代入数据计算 ,即可求出这个 组合图形的表面积 。
组合图形的体积=长方体的体积+正方体的体积 ,根据长方 体的体积=长×宽×高 ,正方体的体积=棱长×棱长×棱长 , 代入数据计算 ,即可求出这个组合图形的体积 。
【详解 】表面积:
(12×10+12×2+10×2)×2+5×5×4 =(120+24+20)×2+5×5×4
= 164×2+25×4
= 328+100
第 8 页 共 30 页
=428(cm2) 体积:
12×10×2+5×5×5 = 240+125
=365(cm3)
组合图形的表面积是428cm2 ,组合图形的体积是 365cm3 。 4 .150 平方分米 ;109 立方分米
【 分析】根据正方体的体积 、表面积的意义 ,从正方体的 顶点上挖掉一个小长方体 ,因为这个小长方体原来外露3 个面 ,挖掉这个小长方体后又外露与原来相同的3 个面 , 所以剩下图形的表面积不变 ,体积减少了一个小长方体的 而体积 ,据此解答即可 。
【详解 】5×5×6 = 25×6
=150(平方分米) 5×5×5-4×2×2
= 125-16
= 109(立方分米)
5 .(1)160cm2 ;128cm3
(2)220cm2 ;187cm3
【 分析 】(1)长方体的表面积=(长×宽+长×高+宽×高)×2 ,长 方体的体积=长×宽×高 ,把长方体的长 13 厘米 、宽 4 厘米 、 高 5 厘米的值分别代入长方体的表面积公式 、体积公式计 算即可 。
(2)通过观察图形可知 ,因为正方体和长方体粘合在一起 , 所以在求表面积时上面的正方体只求它的 4 个侧面的面积 ,
第 9 页 共 30 页
下面的长方体求出表面积 ,然后合并即可; 这个组合图形 的体积等于长方体的体积加上正方体的体积 。根据正方体 的表面积公式:S=6a2 ,体积公式:V=a3 ,长方体的表面 积公式:S=(ab+a h+bh)×2 ,体积公式:V=abh ,把数据代 入公式解答 。
【详解 】(1)(8×4+8×4+4×4)×2 =(32+32+16)×2
= 80×2
= 160(cm2) 8×4×4
= 32×4
= 128(cm3)
长方体的表面积是 160cm2 ,体积是 128cm3 。
(2)(8×4+8×5+4×5)×2+3×3×4
=(32+40+20)×2+9×4 = 92×2+36
= 184+36
=220(cm2) 8×4×5+3×3×3 = 32×5+9×3 = 160+27
= 187(cm3)
组合图形的表面积是 220cm2 ,体积是 187cm3 。
6 .左图表面积是 254 平方厘米 ,体积是 214 立方厘米 ;右 图表面积是236 平方厘米 ,体积是232 立方厘米 。
【 分析】 通过观察图形可知 ,由于上面的正方体和下面的
第 10 页 共 30 页
长方体粘合在一起 ,所以上面的正方体只求它的4 个侧面 的面积 ,下面的长方体求它的表面积 ,然后合并起来即可 , 根据正方体的表面积公式:S=6a2 ,长方体的表面积公式: S=(ab+a h+bh)×2 ,把数据代入公式求出它的表面积 ,根据 正方体的体积公式:V=a3 ,长方体的体积公式:V=abh , 把数据代入公式求出它的体积 。
大长方体挖去一个小正方体 ,凹下去图形的三个面的面积 刚好能补上原来缺失的三个面的面积 ,所以大长方体的表 面积没有改变 。用长方体的表面积公式求解即可 。组合体 的体积用大长方体的体积减去小正方体的体积即可 。
【详解 】
4x4x4+(10x5+10x3+5x3)x2 =16x4+(50+30+15)x2
=64+95x2
=64+190
=254(平方厘米) 4x4x4+10x5x3 =16x4+50x3
=64+150
=214(立方厘米)
它的表面积是254 平方厘米 ,体积是 214 立方厘米 。
(8x6+8x5+6x5)x2 =(48+40+30)x2
=118x2
= 236(平方厘米) 8x6x5-2x2x2
第 11 页 共 30 页
=48x5-4x2
=240-8
=232(立方厘米)
它的表面积是236 平方厘米 ,体积是 232 立方厘米 。 7 .700cm3
【 分析】如图 ,将组合体分成两个长方体, 长方体体积=长×宽×高 ,据此分别求出两个长方体体积 , 相加即可 。
【详解 】 12-8=4(cm) 8×7×10+4×7×5
= 560+140 =700(cm3)
8 .表面积为:49600 平方厘米 ;体积为:640000 立方厘米 【 分析】 图中组合图形的表面积等于长为 100 厘米 ,宽为
80 厘米 ,高为(60+50)厘米的长方体的表面积减去 4 个长为
50 厘米 ,宽为(100-40)÷2 厘米的长方形的面积 ,分别利用 长方体的表面积和长方形的面积公式 ,再相减即可求出组 合图形的表面积;
图中的组合图形的体积等于长为 100 厘米 ,宽为80 厘米 , 高为(60+50)厘米的长方体的体积减去 2 个长为(100-40)÷2 厘米 ,宽为80 厘米 ,高为50 厘米的长方体的体积 ,利用 长方体的体积公式 ,再相减即可求出组合图形的体积 。
【详解 】(100-40)÷2 = 60÷2
第 12 页 共 30 页
=30(厘米)
100×80×2+100×(60+50)×2+80×(60+50)×2-4×50×30 = 16000+100×110×2+80×110×2-6000
= 16000+22000+17600-6000
=49600(平方厘米)
100×80×(60+50)-2×30×80×50 = 100×80×110-4800×50
= 880000-240000
=640000(立方厘米)
即图形的表面积是49600 平方厘米 ,体积是 640000 立方厘 米 。
9 .78cm2 ;38cm3 ; 148cm2 ;108cm3
【 分析】观察图形一可知 ,该图形的体积等于长方体的体 积加上正方体的体积 ,根据长方体的体积公式:V=abh , 正方体的体积公式:V=a3 ,据此代入数值进行计算即可; 该图形的表面积等于长方体的表面积加上正方体的表面积 , 再减去正方体两个面的面积 ,再结合长方体的表面积公式: S=(ab+a h+bh)×2 ,正方体的表面积公式:S=a2×6 ,据此进 行计算即可; 观察图形二可知 ,该长方体的顶点处少了一 个小长方体 ,该图形的表面积与完整图形的表面积相等 , 根据长方体的表面积:S=(ab+a h+bh)×2 ,据此求出该图形 表面积即可; 该图形的长方体的体积等于大长方体的体积 减去小长方体的体积 ,再根据长方体的体积:V=abh ,据 此计算即可 。
【详解 】 图一表面积:(5×3+5×2+3×2)×2+2×2×6-2×2×2
第 13 页 共 30 页
=(15+10+6)×2+4×6-8
= 31×2+24-8
= 62+24-8
= 86-8
=78(cm2)
图一体积:5×3×2+2×2×2 = 15×2+4×2
= 30+8
=38(cm3)
图二表面积:(6×4+6×5+5×4)×2
=(24+30+20)×2 = 74×2
= 148(cm2)
图二体积:6×5×4-3×2×2 = 30×4-6×2
= 120-12
= 108(cm3)
10 .27500 立方厘米
【 分析】 长方体体积=长×宽×高 。空心砖的体积用大方体 的体积减去小长方体的体积即可 。
【详解 】40×30×25-10×10×25 = 1200×25-100×25
= 30000-2500
=27500(立方厘米) 11 .120cm3
【 分析】 水面上升的体积就是铁块的体积 ,长方体容器的
第 14 页 共 30 页
长×宽×上升的水的高度=铁块体积 ,据此列式计算 。 【详解 】 10×8×(9.5-8)
= 80×1.5
= 120(cm3)
12 .1220m2 ;2445m3
【 分析 】长方体的表面积=(长×宽+宽×高+长×高)×2 ,长方 体的体积=长×宽×高 ,几何体的表面积=大长方体的表面 积+小长方体 4 个侧面的面积 ,几何体的体积=大长方体的 体积+小长方体的体积 ,据此解答 。
【详解 】表面积:(20×8+20×15+8×15)×2+5×3×4 =(160+300+120)×2+5×3×4
= 580×2+5×3×4 = 1160+60
= 1220(m2)
体积:20×8×15+5×3×3 = 160×15+15×3
= 2400+45 =2445(m3)
所以 ,这个几何体的表面积是 1220m2 ,体积是 2445m3 。
13 .表面积是 1700 平方分米 ,体积是4104 立方分米
【 分析】 通过观察这个物体的三视图发现 ,一个长方体的 一个角被挖去一个小长方体 ,表面积没有发生变化 ,体积 减少 ,所以直接根据长方体的表面积公式: 长方体的表面 积=(长×宽+长×高+宽×高)×2 即可求出这个物体的表面积 , 然后根据长方体体积公式: 长方体的体积=长×宽×高 ,用 28×15×10-4×4×6 即可求出这个物体的体积 。据此解答 。
第 15 页 共 30 页
【详解 】表面积:(28×10+28×15+15×10)×2
=(280+420+150)×2
= 850×2
=1700(平方分米)
体积:28×15×10-4×4×6 = 4200-96
=4104(立方分米)
该物体的表面积是 1700 平方分米 ,体积是 4104 立方分米 。 14 .700cm2 ;486cm2 ;2160cm3
【 分析 】根据长方体的表面积公式:S=(ab+a h+bh)×2 ,正 方体的表面积公式:S=6a2 ,据此代入数值即可求解; 最 后一个图形的体积等于下面的长方体的体积加上上面长方 体的体积 ,根据长方体的体积公式:V=abh ,据此进行计 算即可 。
【详解 】(15×10+15×8+10×8)×2 =(150+120+80)×2
= 350×2
=700(cm2) 9×9×6
= 81×6
=486(cm2)
15×10×9+10×9×9 = 150×9+90×9 = 1350+810
=2160(cm3)
15 .(1)109cm3
第 16 页 共 30 页
(2)700cm3
【 分析】(1)由图可知 ,图形是正方体中挖空了一个长方体 , 图形的体积=正方体的体积-长方体的体积; 正方体的体积 =棱长×棱长×棱长 ,长方体的体积=长×宽×高;
(2)图形是由长为 12cm ,宽为 7cm ,高为 10cm 的长方体中 , 挖空了一个长为 7cm ,宽为(12-8)cm ,高为 5cm 的小长方体 , 根据公式: 长方体的体积=长×宽×高 ,分别计算出这两个 长方体的体积 ,再相减即可; 据此解答 。
【详解 】(1)5×5×5-4×2×2 = 25×5-8×2
= 125-16
= 109(cm3)
(2)12×7×10-(12-8)×7×5 = 84×10-4×7×5
= 840-28×5 = 840-140 =700(cm3)
16 .158cm2 ;848dm3
【 分析】根据长方体表面积公式: 长方体的表面积=(长× 宽+长×高+宽×高)×2 ,用(8×3+8×5+3×5)×2 即可求出左图长方 体的表面积;
右图由一个棱长为8dm 的正方体和一个长为 14dm 、宽为 12dm 、高为2dm 的长方体组成 ,根据长方体的体积=长× 宽×高和正方体的体积=棱长×棱长×棱长 ,用 14×12×2+8×8× 8 即可求出右图的体积 。
第 17 页 共 30 页
【详解 】(8×3+8×5+3×5)×2
=(24+40+15)×2 = 79×2
= 158cm2
左图的长方体表面积是 158cm2 。
14×12×2+8×8×8 = 336+512
= 848dm3
右图的体积是 848dm3 。
17 .184 平方厘米 ;152 立方厘米
【 分析】观察图形可知 ,该图形的表面积等于长方体的表 面积加上正方体的4 个面的面积 ,根据长方体的表面积公 式:S=(ab+a h+bh)×2 ,正方形的面积公式:S=a2 ,据此进 行计算即可; 该图形的体积等于长方体的体积加上正方体 的体积 ,根据长方体的体积公式:V=abh ,正方体的体积 公式:V=a3 ,据此进行计算即可 。
【详解 】(6×6+6×4+6×4)×2+2×2×4
= 84×2+16
= 168+16
= 184(平方厘米) 6×6×4+2×2×2
= 144+8
= 152(立方厘米)
18 .1800cm2 ;4000cm3
【 分析】 看图 ,一共有 4 个小正方体 ,并且一共有6 个面 被遮盖住了 ,所以只要求 18 个面的面积和 。用棱长×棱长×
第 18 页 共 30 页
18 ,即可求出该图形的表面积;
正方体体积=棱长×棱长×棱长 ,据此先求出 1 个小正方体 的体积 ,再将其乘4 ,求出该图形的体积 。
【详解 】表面积 :10×10×18= 1800(cm2) 体积 :10×10×10×4=4000(cm3)
19 .表面积 384cm2 ;体积 497cm3
【 分析】从图中可知 ,在图形右上方的顶点处挖掉了一个 小长方体 ,露出了3 个面 ,这 3 个面可以向外平移 ,正好 补齐缺口 ,补成一个完整的正方体 ,所以图形的表面积 = 正方体的表面积 ,根据正方体的表面积=棱长×棱长×6 ,代 入数据计算求解 。
图形的体积=正方体的体积-挖掉的小长方体的体积 ,根据 正方体的体积=棱长×棱长×棱长 ,长方体的体积=长×宽× 高 ,代入数据计算求解 。
【详解 】表面积:
8×8×6
= 64×6
=384(cm2) 体积:
8×8×8-2×2.5×3 = 64×8-5×3
= 512-15
=497(cm3)
图形的表面积是 384cm2 ,体积是 497cm3 。
20 .(1)324cm2 ;360cm3
(2)30m2 ;6m3
第 19 页 共 30 页
【 分析 】(1)根据长方体表面积公式 S=(ab+a h+bh)×2 ,体积 公式 V=abh ,代入数据计算求解 。
(2)组合图形的表面积=正方体表面积-长方体上下面的面 积+长方体的侧面积 ,其中长方体上下面是2 个边长为 1m 的正方形 ,长方体的侧面是 4 个相同的长为2m 、宽为 1m 的长方形; 根据正方体的表面积公式 S=6a2 ,正方形的面 积公式 S=a2 ,长方形的面积公式 S=ab ;代入数据计算求 解 ;
组合图形的体积= 正方体的体积-长方体的体积; 根据正方 体的体积公式 V=a3 ,长方体的体积公式 V=abh ,代入数 据计算求解 。
【详解 】(1)表面积:
(12×6+12×5+6×5)×2 =(72+60+30)×2
= 162×2
=324(cm2)
体积:
12×6×5=360(cm3)
长方体的表面积是 324cm2 ,体积是 360cm3 。
(2)表面积:
2×2×6-1×1×2+2×1×4 = 24-2+8
=30(m2)
体积:
2×2×2-1×1×2 = 8-2
第 20 页 共 30 页
=6(m3)
组合图形的表面积是 30m2 ,体积是 6m3 。
五年级数学下册长方体和正方体专训
(
组合图形体积和表面积
)
第 21 页 共 30 页
1. 下图中长方体长 8 厘米 、宽 6 厘米 、高 4 厘米, 正方体的棱长是5 厘米。 请计算组合体的表面积和体积。
(8×6+8×4+6×4)×2+5×5×4 = (48+32+24) ×2+100 = 104×2+100
= 208+ 100
= 308(平方厘米 )
8×6×4+5×5×5
= 192+125
=317(立方厘米)
2. 计算下面立体图形的表面积和体积。
表面积:
(3×1.5+3×1+1.5×1)×2+(1.5+1)×2×1 =(4.5+3+1.5)×2+2.5×2×1
= 9×2+5×1 = 18+5
=23(m2)
体积:3×1.5×1+1×1×1.5
= 4.5×1+1×1.5 = 4.5+1.5
=6(m3)
3. 求出下面组合图形的表面积和体积(单位: cm )。
表面积:
(12×10+12×2+10×2)×2+5×5×4 =(120+24+20)×2+5×5×4
= 164×2+25×4 = 328+100
第 22 页 共 30 页
=428(cm2)
体积:
12×10×2+5×5×5 = 240+125
=365(cm3)
4. 计算如图物体的表面积和体积。(单位: 分米)
5×5×6
= 25×6
=150(平方分米)
5×5×5-4×2×2 = 125-16
= 109(立方分米)
5. 计算下面图形的表面积的和体积。(单位: cm )
(8×4+8×4+4×4)×2 =(32+32+16)×2 = 80×2
= 160(cm2)
8×4×4
= 32×4
= 128(cm3)
(8×4+8×5+4×5)×2+3×3×4
=(32+40+20)×2+9×4 = 92×2+36
= 184+36 =220(cm2)
8×4×5+3×3×3
第 23 页 共 30 页
= 32×5+9×3 = 160+27 = 187(cm3)
6. 求下面各图形的表面积和体积。(单位: 厘米)
4x4x4+(10x5+10x3+5x3)x2 =16x4+(50+30+15)x2
=64+95x2
=64+190
=254(平方厘米)
4x4x4+10x5x3 =16x4+50x3
=64+150
=214(立方厘米)
(8x6+8x5+6x5)x2 =(48+40+30)x2
=118x2
= 236(平方厘米)
8x6x5-2x2x2
=48x5-4x2
=240-8
=232(立方厘米)
7. 求下面图形的体积。(单位: cm )。
12–8=4(cm) 8×7×10+4×7×5 = 560+140
第 24 页 共 30 页
=700(cm3)
8. 计算下面图形的表面积和体积。(单位: 厘米)
(100-40)÷2 = 60÷2
=30(厘米)
100×80×2+100×(60+50)×2+80×(60+50)×2-4×50×30 = 16000+100×110×2+80×110×2-6000
= 16000+22000+17600-6000
=49600(平方厘米)
100×80×(60+50)-2×30×80×50 = 100×80×110-4800×50
= 880000-240000
=640000(立方厘米)
9. 求下图形的表面积和体积。(单位: cm )
图一表面积:
(5×3+5×2+3×2)×2+2×2×6-2×2×2 =(15+10+6)×2+4×6-8
= 31×2+24-8
= 62+24-8
= 86-8
=78(cm2)
体积:5×3×2+2×2×2
= 15×2+4×2 = 30+8
=38(cm3)
图二表面积:
第 25 页 共 30 页
(6×4+6×5+5×4)×2 =(24+30+20)×2 = 74×2
= 148(cm2)
体积:6×5×4=3×2×2 = 30×4-6×2
= 120-12
= 108(cm3)
10. 图形计算, 计算这块空心砖的体积。(单位: 厘米)
40×30×25-10×10×25 = 1200×25-100×25 = 30000-2500
= 27500(立方厘米)
11. 铁块的体积是多少 cm3?
10×8×(9.5-8) = 80×1.5
= 120(cm3)
12. 计算下面几何体的表面积和体积。
表面积:
(
=
580×2+5×3×4
)(20×8+20×15+8×15)×2+5×3×4 =(160+300+120)×2+5×3×4
第 26 页 共 30 页
= 1160+60 = 1220(m2)
体积:20×8×15+5×3×3 = 160×15+15×3
= 2400+45 =2445(m3)
13. 如图, 求该物体的表面积和体积。(单位: 分米)
表面积:
(28×10+28×15+15×10)×2 =(280+420+150)×2
= 850×2
=1700(平方分米)
体积:28×15×10-4×4×6 = 4200-96
=4104(立方分米)
14.求下面前两个图形的表面积,求最后一个图形的体积。(单位:cm )
(15×10+15×8+10×8)×2 =(150+120+80)×2
= 350×2
=700(cm2)
9×9×6 = 81×6
=486(cm2)
15×10×9+10×9×9 = 150×9+90×9 = 1350+810
第 27 页 共 30 页
=2160(cm3)
15. 计算下列图形的体积。(单位: cm )
5×5×5-4×2×2 = 25×5-8×2 = 125-16
= 109(cm3)
12×7×10-(12-8)×7×5 = 84×10-4×7×5
= 840-28×5 = 840-140
=700(cm3)
16. 计算下左图的表面积和下右图的体积。
(8×3+8×5+3×5)×2 =(24+40+15)×2 = 79×2
= 158cm2
14×12×2+8×8×8 = 336+512
= 848dm3
17. 计算下面图形的表面积和体积。
(6×6+6×4+6×4)×2+2×2×4 = 84×2+16
= 168+16
= 184(平方厘米)
6×6×4+2×2×2
= 144+8
= 152(立方厘米)
第 28 页 共 30 页
18. 如图, 计算出该图形的表面积和体积。(单位: cm )
表面积:
10×10×18= 1800(cm2)
体积:
10×10×10×4=4000(cm3)
19. 计算下面图形的表面积和体积。(单位: cm )
表面积:
8×8×6
= 64×6
=384(cm2)
体积:
8×8×8-2×2.5×3 = 64×8-5×3
= 512-15
=497(cm3)
20. 求下列立体图形的表面积与体积。
表面积:
(12×6+12×5+6×5)×2 =(72+60+30)×2
= 162×2
=324(cm2)
体积:
12×6×5=360(cm3)
表面积:
2×2×6-1×1×2+2×1×4
= 24-2+8
第 29 页 共 30 页
=30(m2)
体积:
2×2×2-1×1×2 = 8-2 =6(m3)
第 30 页 共 30 页
