2024-2025学年北师版七年级(初一)数学下册期末考试模拟卷(含解析)
文档属性
| 名称 | 2024-2025学年北师版七年级(初一)数学下册期末考试模拟卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览


文档简介
2024-2025学年七年级数学下学期期末模拟卷
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:北师大版七年级下册全部。
5.难度系数:0.65。
第一部分(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,满分24分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列汉字是轴对称图形的是( )
A. B. C. D.
2.气凝胶是一种具有纳米多孔结构的新型材料,质量轻、隔热能力强,可应用于航天、军工、建筑等领域,气凝胶颗粒尺寸通常小于.数据“”用科学记数法表示为( )
A. B. C. D.
3.如图,若,则下列结论正确的是( )
A. B. C. D.
4.一个三角形的两边长分别为2和5,第三边长为奇数,则该三角形的周长为( )
A.13 B.12 C.11 D.10
5.下列计算正确的是( )
A. B. C. D.
6.如图,把长短确定的两根木棍、的一端固定在处,和第三根木棍摆出,再将木棍绕转动,得到,这个实验说明( )
A.有两角和其中一角的对边分别相等的两个三角形不一定全等
B.有两边和其中一边的对角分别相等的两个三角形一定不全等
C.有两边和它们的夹角分别相等的两个三角形不一定全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如表,以下说法错误的是( )
刹车时车速 0 10 20 30 40 50
刹车距离 0 2.5 5 7.5 10 12.5
A.在变化中,刹车时车速是自变量,刹车距离是因变量
B.随的增大而增大
C.当刹车时车速为时,刹车距离是
D.在限速的高速公路上,最大刹车距离为
8.如图1,已知和关于直线对称;在射线上取点E,连接,,如图2;在射线上取点F连接,,如图3,依此规律,第n个图形中全等三角形的对数是( )
A.n B. C. D.
第二部分(非选择题 共96分)
二、填空题(本大题共5小题,每小题3分,满分15分)
9.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽的概率是 .
10.已知,则等于 .
11.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作,垂足为点F,若,则的度数为 .
12.等腰三角形的两边长分别为和,则三角形的周长为 .
13.如图,在面积为的中,,,于点,直线垂直平分交于点,交于点,为直线上一动点,则周长的最小值为 .
三、解答题(本大题共13小题,满分81分.解答应写出文字说明,证明过程或演算步骤)
14.(5分)计算:
15.(5分)先化简,再求值:,其中.
16.(5分)已知,如图,在,,于,平分,,求的度数.
17.(5分)如图,已知点在的边上,利用尺规作图法在内作,使得点在射线上,且.(不写作法,保留作图痕迹)
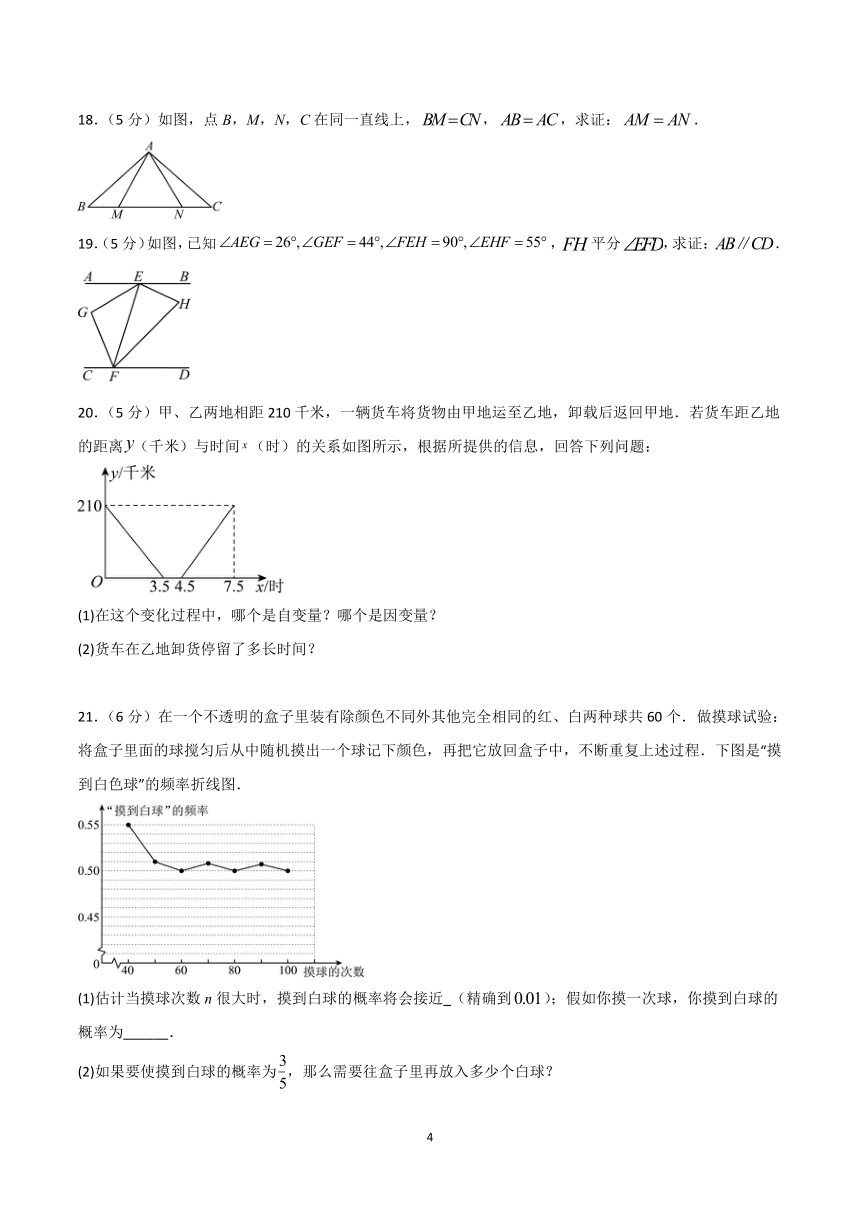
18.(5分)如图,点B,M,N,C在同一直线上,,,求证:.
19.(5分)如图,已知,平分,求证:.
20.(5分)甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离(千米)与时间(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)在这个变化过程中,哪个是自变量?哪个是因变量?
(2)货车在乙地卸货停留了多长时间?
21.(6分)在一个不透明的盒子里装有除颜色不同外其他完全相同的红、白两种球共60个.做摸球试验:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.下图是“摸到白色球”的频率折线图.
(1)估计当摸球次数n很大时,摸到白球的概率将会接近 (精确到);假如你摸一次球,你摸到白球的概率为______.
(2)如果要使摸到白球的概率为,那么需要往盒子里再放入多少个白球?
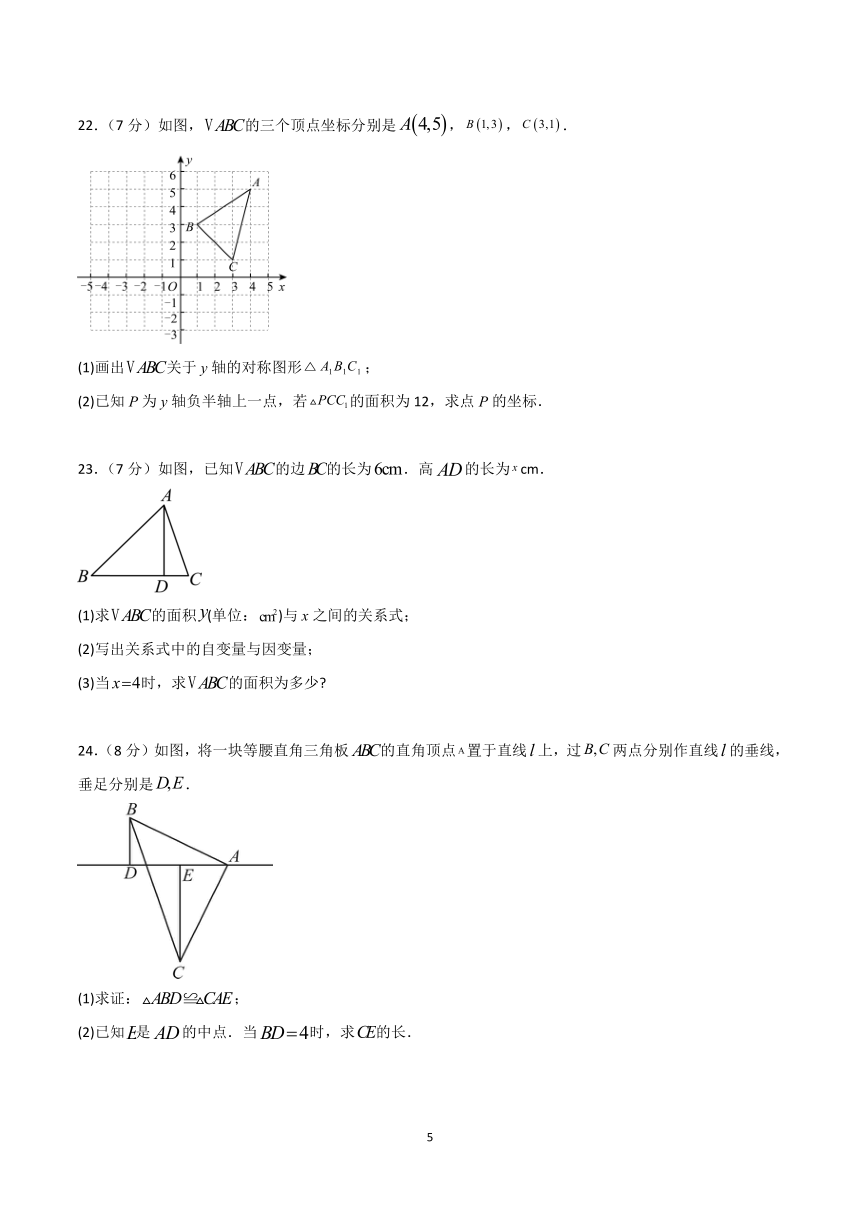
22.(7分)如图,的三个顶点坐标分别是,,.
(1)画出关于y轴的对称图形;
(2)已知P为y轴负半轴上一点,若的面积为12,求点P的坐标.
23.(7分)如图,已知的边的长为.高的长为cm.
(1)求的面积(单位:)与x之间的关系式;
(2)写出关系式中的自变量与因变量;
(3)当时,求的面积为多少
24.(8分)如图,将一块等腰直角三角板的直角顶点置于直线上,过两点分别作直线的垂线,垂足分别是.
(1)求证:;
(2)已知是的中点.当时,求的长.
25.(8分)图1是长为,宽为的长方形,沿图中的虚线将该长方形裁剪成四块长为,宽为的小长方形,然后按图2方式拼成一个正方形.
(1)根据图形可知,图2中,大正方形的边长为_______,阴影部分的面积为_________;
(2)观察图2的面积可知,代数式,和之间存在一定的等量关系,请直接写出这个等量关系__________;
(3)根据(2)中得到的等量关系,解决问题:已知小长方形的周长为,面积为,则求阴影部分的面积.
26.(10分)【问题探究】
(1)如图1,在中,点是上一点,点是的中点,连接并延长到点,过点作交于点,连接,求证:;
【问题解决】
(2)如图2,四边形是一个工业区,点是一个入口,是两个仓库,点分别是粗加工厂和精密加工厂,点分别在上,是两条小路,是两条运输公路,为方便从粗加工厂运输到精密加工厂,现要沿修建一个运输轨道,为了估计成本,现管理人员需要知道运输轨道与运输公路之间的数量关系.已知,.请你帮助管理人员探索线段之间的数量关系,并加以证明.
2024-2025学年七年级数学下学期期末模拟卷
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:北师大版七年级下册全部。
5.难度系数:0.65。
第一部分(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,满分24分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列汉字是轴对称图形的是( )
A. B. C. D.
【答案】B
【详解】解:A、C、D选项中的汉字都不能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称汉字;
B选项中的汉字能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称汉字;
故选:B.
2.气凝胶是一种具有纳米多孔结构的新型材料,质量轻、隔热能力强,可应用于航天、军工、建筑等领域,气凝胶颗粒尺寸通常小于.数据“”用科学记数法表示为( )
A. B. C. D.
【答案】A
【详解】解:,
故选:A.
3.如图,若,则下列结论正确的是( )
A. B. C. D.
【答案】A
【详解】解:∵,
∴(同位角相等,两直线平行),
故选:A.
4.一个三角形的两边长分别为2和5,第三边长为奇数,则该三角形的周长为( )
A.13 B.12 C.11 D.10
【答案】B
【详解】解:∵一个三角形的两边长分别为2和5,
∴第三边,即第三边,
∵第三边长为奇数,
∴第三边长为5,
∴该三角形的周长为,
故选:B.
5.下列计算正确的是( )
A. B.
C. D.
【答案】B
【详解】解:、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
、,该选项错误,不合题意;
故选:.
6.如图,把长短确定的两根木棍、的一端固定在处,和第三根木棍摆出,再将木棍绕转动,得到,这个实验说明( )
A.有两角和其中一角的对边分别相等的两个三角形不一定全等
B.有两边和其中一边的对角分别相等的两个三角形一定不全等
C.有两边和它们的夹角分别相等的两个三角形不一定全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
【答案】D
【详解】解:由题意可知:,,,
满足有两边和其中一边的对角分别相等,但是和不全等,
有两边和其中一边的对角分别相等的两个三角形不一定全等.
故选:.
7.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如表,以下说法错误的是( )
刹车时车速 0 10 20 30 40 50
刹车距离 0 2.5 5 7.5 10 12.5
A.在变化中,刹车时车速是自变量,刹车距离是因变量
B.随的增大而增大
C.当刹车时车速为时,刹车距离是
D.在限速的高速公路上,最大刹车距离为
【答案】C
【详解】解:在变化中,刹车时车速是自变量,刹车距离是因变量,故A正确,不符合题意;
由表格可得:随的增大而增大,当刹车时车速每增加,刹车距离增加,故B正确,不符合题意;
当刹车时车速为时,刹车距离是,故C错误,符合题意;
在限速的高速公路上,最大刹车距离为,故D正确,不符合题意;
故选:C.
8.如图1,已知和关于直线对称;在射线上取点E,连接,,如图2;在射线上取点F连接,,如图3,依此规律,第n个图形中全等三角形的对数是( )
A.n B. C. D.
【答案】C
【详解】解:∵和关于直线对称,
∴,,
在与中,
,
∴.
∴图1中有1对三角形全等;
同理图2中,,
∴,
∵,
∴,
在和中,
,
∴,
∴图2中有对三角形全等;
同理:图3中有对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
第二部分(非选择题 共96分)
二、填空题(本大题共5小题,每小题3分,满分15分)
9.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽的概率是 .
【答案】
【详解】解:共有5位数学家,赵爽是其中一位,
所以,从中任选一个,恰好是赵爽的概率是,
故答案为:
10.已知,则等于 .
【答案】6
【详解】解:∵,,
∴,
故答案为:6.
11.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作,垂足为点F,若,则的度数为 .
【答案】或35度
【详解】解:∵,
∴,
∴,
∵,
∴,
∴.
故答案为:.
12.等腰三角形的两边长分别为和,则三角形的周长为 .
【答案】
【详解】解:该三角形是等腰三角形,
边长组成有两种情况:,,或,,,
,即不符合三角形三边关系,
舍去,
三角形的周长为.
故答案为:.
13.如图,在面积为的中,,,于点,直线垂直平分交于点,交于点,为直线上一动点,则周长的最小值为 .
【答案】
【详解】解:如图,连接,
∵,,,
∴,
∵的面积为,
∴,
∴,
∵垂直平分,
∴,
∵为直线上一动点,
∴,
∴,
∴,
∴周长的最小值为.
故答案为:.
三、解答题(本大题共13小题,满分81分.解答应写出文字说明,证明过程或演算步骤)
14.(5分)计算:
【详解】解:原式(2分)
(4分)
(5分)
15.(5分)先化简,再求值:,其中.
【详解】解:
(3分)
(4分)
当时,原式.(5分)
16.(5分)已知,如图,在,,于,平分,,求的度数.
【详解】解:∵,,
∴,(2分)
∵,
∴,(4分)
∵平分,
∴.(5分)
17.(5分)如图,已知点在的边上,利用尺规作图法在内作,使得点在射线上,且.(不写作法,保留作图痕迹)
【详解】解:如图,点D即为所求.
(5分)
18.(5分)如图,点B,M,N,C在同一直线上,,,求证:.
【详解】证明:∵,
∴,(1分)
在与中,(3分)
∴,(4分)
∴.(5分)
19.(5分)如图,已知,平分,求证:.
【详解】解:,
,(1分)
,
,(2分)
平分,
,(3分)
,
,(4分)
.(5分)
20.(5分)甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离(千米)与时间(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)在这个变化过程中,哪个是自变量?哪个是因变量?
(2)货车在乙地卸货停留了多长时间?
【详解】(1)解:由题意得:时间x是自变量,货车距乙地的距离y是因变量.(2分)
(2)解:由图象可得:(小时),
答:货车在乙地卸货停留了1小时.(5分)
21.(6分)在一个不透明的盒子里装有除颜色不同外其他完全相同的红、白两种球共60个.做摸球试验:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.下图是“摸到白色球”的频率折线图.
(1)估计当摸球次数n很大时,摸到白球的概率将会接近 (精确到);假如你摸一次球,你摸到白球的概率为______.
(2)如果要使摸到白球的概率为,那么需要往盒子里再放入多少个白球?
【详解】(1)解:估计当摸球次数n很大时,摸到白球的概率将会接近;假如你摸一次球,你摸到白球的概率为;(2分)
(2)解:由题意,可知白球的个数为(个),红球的个数为(个).(3分)
设需要往盒子里再放入个白球.
根据题意,得,解得.(6分)
答:需要往盒子里再放入15个白球.
22.(7分)如图,的三个顶点坐标分别是,,.
(1)画出关于y轴的对称图形;
(2)已知P为y轴负半轴上一点,若的面积为12,求点P的坐标.
【详解】(1)解:如图,△即为所求.
(3分)
(2)解:设点的坐标为,(4分)
的面积为12,,
,(5分)
解得,(6分)
点的坐标为.(7分)
故答案为:.
23.(7分)如图,已知的边的长为.高的长为cm.
(1)求的面积(单位:)与x之间的关系式;
(2)写出关系式中的自变量与因变量;
(3)当时,求的面积为多少
【详解】(1)解:∵的边的长为.高的长为cm,的面积为,
∴;(3分)
(2)是自变量,是因变量(5分)
(3)当时,,(6分)
∴当时,求的面积为.(7分)
24.(8分)如图,将一块等腰直角三角板的直角顶点置于直线上,过两点分别作直线的垂线,垂足分别是.
(1)求证:;
(2)已知是的中点.当时,求的长.
【详解】(1)证明:∵是等腰直角三角形,
∴,
∴.(1分)
∵,
∴,
∴,
∴.(3分)
在和中,
∴;(5分)
(2)解:,
∴.
∵是的中点,,(7分)
∴,即的长为8.(8分)
25.(8分)图1是长为,宽为的长方形,沿图中的虚线将该长方形裁剪成四块长为,宽为的小长方形,然后按图2方式拼成一个正方形.
(1)根据图形可知,图2中,大正方形的边长为_______,阴影部分的面积为_________;
(2)观察图2的面积可知,代数式,和之间存在一定的等量关系,请直接写出这个等量关系__________;
(3)根据(2)中得到的等量关系,解决问题:已知小长方形的周长为,面积为,则求阴影部分的面积.
【详解】(1)解:根据图形可知,图2中,大正方形的边长为,阴影部分正方形的边长为,
∴阴影部分的面积为,
故答案为:;;(2分)
(2)由(1)知:图2中阴影部分的面积为,
阴影部分的面积也可以看作大正方形与个小长方形的面积差,即为,
∴代数式,和之间的数量关系是:;(5分)
(3)解:这个小长方形的长为,宽为,则,,
∴,(6分)
由(2)知:,
∴阴影部分的面积是.(8分)
26.(10分)【问题探究】
(1)如图1,在中,点是上一点,点是的中点,连接并延长到点,过点作交于点,连接,求证:;
【问题解决】
(2)如图2,四边形是一个工业区,点是一个入口,是两个仓库,点分别是粗加工厂和精密加工厂,点分别在上,是两条小路,是两条运输公路,为方便从粗加工厂运输到精密加工厂,现要沿修建一个运输轨道,为了估计成本,现管理人员需要知道运输轨道与运输公路之间的数量关系.已知,.请你帮助管理人员探索线段之间的数量关系,并加以证明.
【详解】证明:(1)点是的中点,
,
,
,
.(2分)
,
垂直平分 ,
,
在 中,
,
.(4分)
(2),
证明如下:
如图,延长至点,使 ,连接 ,
,
,(5分)
在和中,
,
,(7分)
,
在和中,
,
,(9分)
,
.(10分)
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:北师大版七年级下册全部。
5.难度系数:0.65。
第一部分(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,满分24分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列汉字是轴对称图形的是( )
A. B. C. D.
2.气凝胶是一种具有纳米多孔结构的新型材料,质量轻、隔热能力强,可应用于航天、军工、建筑等领域,气凝胶颗粒尺寸通常小于.数据“”用科学记数法表示为( )
A. B. C. D.
3.如图,若,则下列结论正确的是( )
A. B. C. D.
4.一个三角形的两边长分别为2和5,第三边长为奇数,则该三角形的周长为( )
A.13 B.12 C.11 D.10
5.下列计算正确的是( )
A. B. C. D.
6.如图,把长短确定的两根木棍、的一端固定在处,和第三根木棍摆出,再将木棍绕转动,得到,这个实验说明( )
A.有两角和其中一角的对边分别相等的两个三角形不一定全等
B.有两边和其中一边的对角分别相等的两个三角形一定不全等
C.有两边和它们的夹角分别相等的两个三角形不一定全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如表,以下说法错误的是( )
刹车时车速 0 10 20 30 40 50
刹车距离 0 2.5 5 7.5 10 12.5
A.在变化中,刹车时车速是自变量,刹车距离是因变量
B.随的增大而增大
C.当刹车时车速为时,刹车距离是
D.在限速的高速公路上,最大刹车距离为
8.如图1,已知和关于直线对称;在射线上取点E,连接,,如图2;在射线上取点F连接,,如图3,依此规律,第n个图形中全等三角形的对数是( )
A.n B. C. D.
第二部分(非选择题 共96分)
二、填空题(本大题共5小题,每小题3分,满分15分)
9.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽的概率是 .
10.已知,则等于 .
11.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作,垂足为点F,若,则的度数为 .
12.等腰三角形的两边长分别为和,则三角形的周长为 .
13.如图,在面积为的中,,,于点,直线垂直平分交于点,交于点,为直线上一动点,则周长的最小值为 .
三、解答题(本大题共13小题,满分81分.解答应写出文字说明,证明过程或演算步骤)
14.(5分)计算:
15.(5分)先化简,再求值:,其中.
16.(5分)已知,如图,在,,于,平分,,求的度数.
17.(5分)如图,已知点在的边上,利用尺规作图法在内作,使得点在射线上,且.(不写作法,保留作图痕迹)
18.(5分)如图,点B,M,N,C在同一直线上,,,求证:.
19.(5分)如图,已知,平分,求证:.
20.(5分)甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离(千米)与时间(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)在这个变化过程中,哪个是自变量?哪个是因变量?
(2)货车在乙地卸货停留了多长时间?
21.(6分)在一个不透明的盒子里装有除颜色不同外其他完全相同的红、白两种球共60个.做摸球试验:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.下图是“摸到白色球”的频率折线图.
(1)估计当摸球次数n很大时,摸到白球的概率将会接近 (精确到);假如你摸一次球,你摸到白球的概率为______.
(2)如果要使摸到白球的概率为,那么需要往盒子里再放入多少个白球?
22.(7分)如图,的三个顶点坐标分别是,,.
(1)画出关于y轴的对称图形;
(2)已知P为y轴负半轴上一点,若的面积为12,求点P的坐标.
23.(7分)如图,已知的边的长为.高的长为cm.
(1)求的面积(单位:)与x之间的关系式;
(2)写出关系式中的自变量与因变量;
(3)当时,求的面积为多少
24.(8分)如图,将一块等腰直角三角板的直角顶点置于直线上,过两点分别作直线的垂线,垂足分别是.
(1)求证:;
(2)已知是的中点.当时,求的长.
25.(8分)图1是长为,宽为的长方形,沿图中的虚线将该长方形裁剪成四块长为,宽为的小长方形,然后按图2方式拼成一个正方形.
(1)根据图形可知,图2中,大正方形的边长为_______,阴影部分的面积为_________;
(2)观察图2的面积可知,代数式,和之间存在一定的等量关系,请直接写出这个等量关系__________;
(3)根据(2)中得到的等量关系,解决问题:已知小长方形的周长为,面积为,则求阴影部分的面积.
26.(10分)【问题探究】
(1)如图1,在中,点是上一点,点是的中点,连接并延长到点,过点作交于点,连接,求证:;
【问题解决】
(2)如图2,四边形是一个工业区,点是一个入口,是两个仓库,点分别是粗加工厂和精密加工厂,点分别在上,是两条小路,是两条运输公路,为方便从粗加工厂运输到精密加工厂,现要沿修建一个运输轨道,为了估计成本,现管理人员需要知道运输轨道与运输公路之间的数量关系.已知,.请你帮助管理人员探索线段之间的数量关系,并加以证明.
2024-2025学年七年级数学下学期期末模拟卷
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:北师大版七年级下册全部。
5.难度系数:0.65。
第一部分(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,满分24分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列汉字是轴对称图形的是( )
A. B. C. D.
【答案】B
【详解】解:A、C、D选项中的汉字都不能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称汉字;
B选项中的汉字能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称汉字;
故选:B.
2.气凝胶是一种具有纳米多孔结构的新型材料,质量轻、隔热能力强,可应用于航天、军工、建筑等领域,气凝胶颗粒尺寸通常小于.数据“”用科学记数法表示为( )
A. B. C. D.
【答案】A
【详解】解:,
故选:A.
3.如图,若,则下列结论正确的是( )
A. B. C. D.
【答案】A
【详解】解:∵,
∴(同位角相等,两直线平行),
故选:A.
4.一个三角形的两边长分别为2和5,第三边长为奇数,则该三角形的周长为( )
A.13 B.12 C.11 D.10
【答案】B
【详解】解:∵一个三角形的两边长分别为2和5,
∴第三边,即第三边,
∵第三边长为奇数,
∴第三边长为5,
∴该三角形的周长为,
故选:B.
5.下列计算正确的是( )
A. B.
C. D.
【答案】B
【详解】解:、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
、,该选项错误,不合题意;
故选:.
6.如图,把长短确定的两根木棍、的一端固定在处,和第三根木棍摆出,再将木棍绕转动,得到,这个实验说明( )
A.有两角和其中一角的对边分别相等的两个三角形不一定全等
B.有两边和其中一边的对角分别相等的两个三角形一定不全等
C.有两边和它们的夹角分别相等的两个三角形不一定全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
【答案】D
【详解】解:由题意可知:,,,
满足有两边和其中一边的对角分别相等,但是和不全等,
有两边和其中一边的对角分别相等的两个三角形不一定全等.
故选:.
7.为了测定某种型号小型载客汽车的刹车性能(车速不超过),对这种型号的汽车进行了测试,测得的数据如表,以下说法错误的是( )
刹车时车速 0 10 20 30 40 50
刹车距离 0 2.5 5 7.5 10 12.5
A.在变化中,刹车时车速是自变量,刹车距离是因变量
B.随的增大而增大
C.当刹车时车速为时,刹车距离是
D.在限速的高速公路上,最大刹车距离为
【答案】C
【详解】解:在变化中,刹车时车速是自变量,刹车距离是因变量,故A正确,不符合题意;
由表格可得:随的增大而增大,当刹车时车速每增加,刹车距离增加,故B正确,不符合题意;
当刹车时车速为时,刹车距离是,故C错误,符合题意;
在限速的高速公路上,最大刹车距离为,故D正确,不符合题意;
故选:C.
8.如图1,已知和关于直线对称;在射线上取点E,连接,,如图2;在射线上取点F连接,,如图3,依此规律,第n个图形中全等三角形的对数是( )
A.n B. C. D.
【答案】C
【详解】解:∵和关于直线对称,
∴,,
在与中,
,
∴.
∴图1中有1对三角形全等;
同理图2中,,
∴,
∵,
∴,
在和中,
,
∴,
∴图2中有对三角形全等;
同理:图3中有对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
第二部分(非选择题 共96分)
二、填空题(本大题共5小题,每小题3分,满分15分)
9.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽的概率是 .
【答案】
【详解】解:共有5位数学家,赵爽是其中一位,
所以,从中任选一个,恰好是赵爽的概率是,
故答案为:
10.已知,则等于 .
【答案】6
【详解】解:∵,,
∴,
故答案为:6.
11.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作,垂足为点F,若,则的度数为 .
【答案】或35度
【详解】解:∵,
∴,
∴,
∵,
∴,
∴.
故答案为:.
12.等腰三角形的两边长分别为和,则三角形的周长为 .
【答案】
【详解】解:该三角形是等腰三角形,
边长组成有两种情况:,,或,,,
,即不符合三角形三边关系,
舍去,
三角形的周长为.
故答案为:.
13.如图,在面积为的中,,,于点,直线垂直平分交于点,交于点,为直线上一动点,则周长的最小值为 .
【答案】
【详解】解:如图,连接,
∵,,,
∴,
∵的面积为,
∴,
∴,
∵垂直平分,
∴,
∵为直线上一动点,
∴,
∴,
∴,
∴周长的最小值为.
故答案为:.
三、解答题(本大题共13小题,满分81分.解答应写出文字说明,证明过程或演算步骤)
14.(5分)计算:
【详解】解:原式(2分)
(4分)
(5分)
15.(5分)先化简,再求值:,其中.
【详解】解:
(3分)
(4分)
当时,原式.(5分)
16.(5分)已知,如图,在,,于,平分,,求的度数.
【详解】解:∵,,
∴,(2分)
∵,
∴,(4分)
∵平分,
∴.(5分)
17.(5分)如图,已知点在的边上,利用尺规作图法在内作,使得点在射线上,且.(不写作法,保留作图痕迹)
【详解】解:如图,点D即为所求.
(5分)
18.(5分)如图,点B,M,N,C在同一直线上,,,求证:.
【详解】证明:∵,
∴,(1分)
在与中,(3分)
∴,(4分)
∴.(5分)
19.(5分)如图,已知,平分,求证:.
【详解】解:,
,(1分)
,
,(2分)
平分,
,(3分)
,
,(4分)
.(5分)
20.(5分)甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离(千米)与时间(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)在这个变化过程中,哪个是自变量?哪个是因变量?
(2)货车在乙地卸货停留了多长时间?
【详解】(1)解:由题意得:时间x是自变量,货车距乙地的距离y是因变量.(2分)
(2)解:由图象可得:(小时),
答:货车在乙地卸货停留了1小时.(5分)
21.(6分)在一个不透明的盒子里装有除颜色不同外其他完全相同的红、白两种球共60个.做摸球试验:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.下图是“摸到白色球”的频率折线图.
(1)估计当摸球次数n很大时,摸到白球的概率将会接近 (精确到);假如你摸一次球,你摸到白球的概率为______.
(2)如果要使摸到白球的概率为,那么需要往盒子里再放入多少个白球?
【详解】(1)解:估计当摸球次数n很大时,摸到白球的概率将会接近;假如你摸一次球,你摸到白球的概率为;(2分)
(2)解:由题意,可知白球的个数为(个),红球的个数为(个).(3分)
设需要往盒子里再放入个白球.
根据题意,得,解得.(6分)
答:需要往盒子里再放入15个白球.
22.(7分)如图,的三个顶点坐标分别是,,.
(1)画出关于y轴的对称图形;
(2)已知P为y轴负半轴上一点,若的面积为12,求点P的坐标.
【详解】(1)解:如图,△即为所求.
(3分)
(2)解:设点的坐标为,(4分)
的面积为12,,
,(5分)
解得,(6分)
点的坐标为.(7分)
故答案为:.
23.(7分)如图,已知的边的长为.高的长为cm.
(1)求的面积(单位:)与x之间的关系式;
(2)写出关系式中的自变量与因变量;
(3)当时,求的面积为多少
【详解】(1)解:∵的边的长为.高的长为cm,的面积为,
∴;(3分)
(2)是自变量,是因变量(5分)
(3)当时,,(6分)
∴当时,求的面积为.(7分)
24.(8分)如图,将一块等腰直角三角板的直角顶点置于直线上,过两点分别作直线的垂线,垂足分别是.
(1)求证:;
(2)已知是的中点.当时,求的长.
【详解】(1)证明:∵是等腰直角三角形,
∴,
∴.(1分)
∵,
∴,
∴,
∴.(3分)
在和中,
∴;(5分)
(2)解:,
∴.
∵是的中点,,(7分)
∴,即的长为8.(8分)
25.(8分)图1是长为,宽为的长方形,沿图中的虚线将该长方形裁剪成四块长为,宽为的小长方形,然后按图2方式拼成一个正方形.
(1)根据图形可知,图2中,大正方形的边长为_______,阴影部分的面积为_________;
(2)观察图2的面积可知,代数式,和之间存在一定的等量关系,请直接写出这个等量关系__________;
(3)根据(2)中得到的等量关系,解决问题:已知小长方形的周长为,面积为,则求阴影部分的面积.
【详解】(1)解:根据图形可知,图2中,大正方形的边长为,阴影部分正方形的边长为,
∴阴影部分的面积为,
故答案为:;;(2分)
(2)由(1)知:图2中阴影部分的面积为,
阴影部分的面积也可以看作大正方形与个小长方形的面积差,即为,
∴代数式,和之间的数量关系是:;(5分)
(3)解:这个小长方形的长为,宽为,则,,
∴,(6分)
由(2)知:,
∴阴影部分的面积是.(8分)
26.(10分)【问题探究】
(1)如图1,在中,点是上一点,点是的中点,连接并延长到点,过点作交于点,连接,求证:;
【问题解决】
(2)如图2,四边形是一个工业区,点是一个入口,是两个仓库,点分别是粗加工厂和精密加工厂,点分别在上,是两条小路,是两条运输公路,为方便从粗加工厂运输到精密加工厂,现要沿修建一个运输轨道,为了估计成本,现管理人员需要知道运输轨道与运输公路之间的数量关系.已知,.请你帮助管理人员探索线段之间的数量关系,并加以证明.
【详解】证明:(1)点是的中点,
,
,
,
.(2分)
,
垂直平分 ,
,
在 中,
,
.(4分)
(2),
证明如下:
如图,延长至点,使 ,连接 ,
,
,(5分)
在和中,
,
,(7分)
,
在和中,
,
,(9分)
,
.(10分)
同课章节目录
