2024--2025学年 北师大版七年级下册数学期末自测试题(含答案)
文档属性
| 名称 | 2024--2025学年 北师大版七年级下册数学期末自测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 819.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览


文档简介
七年级(下)期末数学试卷2(北师大版)
一、选择题(共10小题,每小题3分,满分30分)
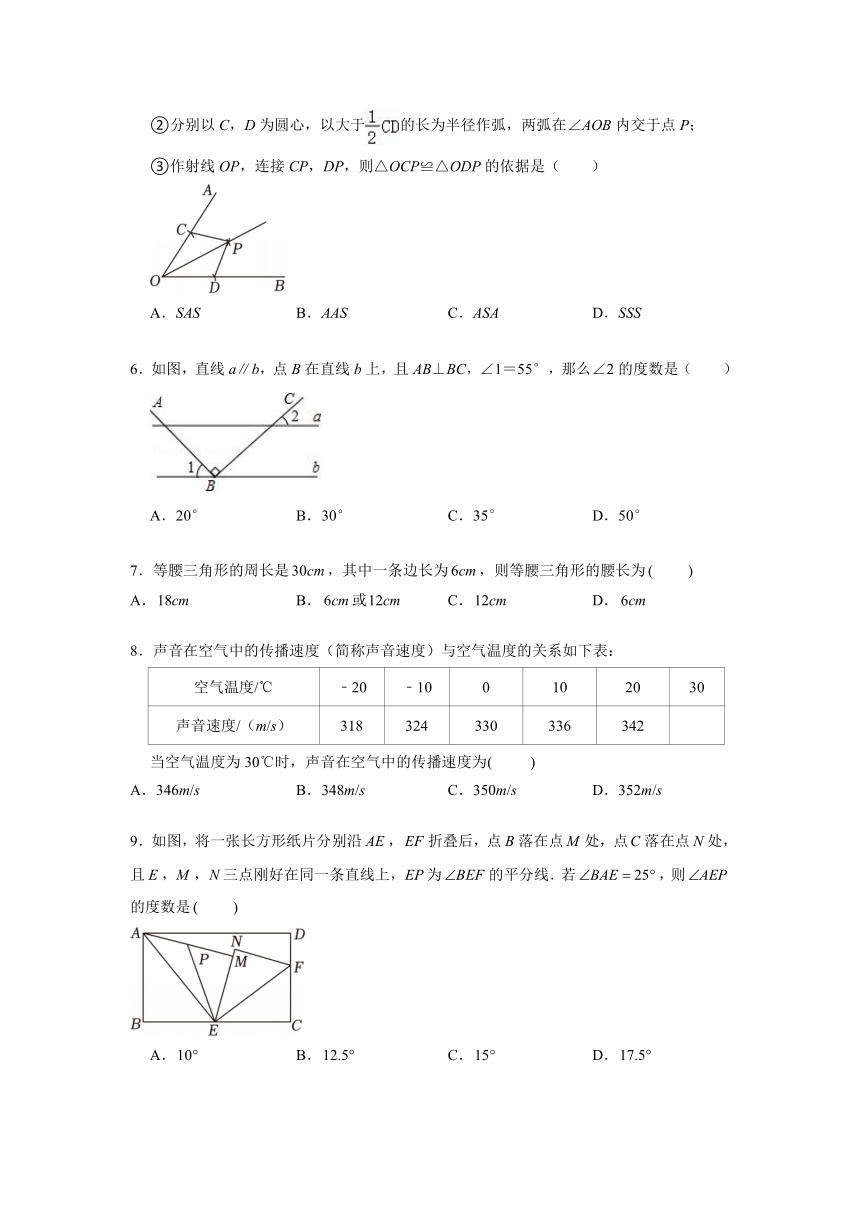
1.下列数学经典图形中,其中是轴对称图形的是( )
A. B.
C. D.
2.计算的结果是
A. B. C. D.
3.下列说法正确的是( )
A.随意掷一枚均匀的硬币两次,至少有一次反面朝上
B.同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,两次点数之和为2是不可能事件
C.某同学在足球训练时,射门5次,射中4次,则可断定他射门命中的概率一定为80%
D.“从一副扑克牌中抽一张,恰好是大王”是随机事件
4.如图,在体育课上,李老师测量学生的跳远成绩的依据是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.过一点有且只有一条直线与已知直线垂直
5.阅读下列作图步骤:
①在OA和OB上分别截取OC,OD,使OC=OD;
②分别以C,D为圆心,以大于的长为半径作弧,两弧在∠AOB内交于点P;
③作射线OP,连接CP,DP,则△OCP≌△ODP的依据是( )
A.SAS B.AAS C.ASA D.SSS
6.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
A.20° B.30° C.35° D.50°
7.等腰三角形的周长是,其中一条边长为,则等腰三角形的腰长为
A. B.或 C. D.
8.声音在空气中的传播速度(简称声音速度)与空气温度的关系如下表:
空气温度/℃ ﹣20 ﹣10 0 10 20 30
声音速度/(m/s) 318 324 330 336 342
当空气温度为30℃时,声音在空气中的传播速度为( )
A.346m/s B.348m/s C.350m/s D.352m/s
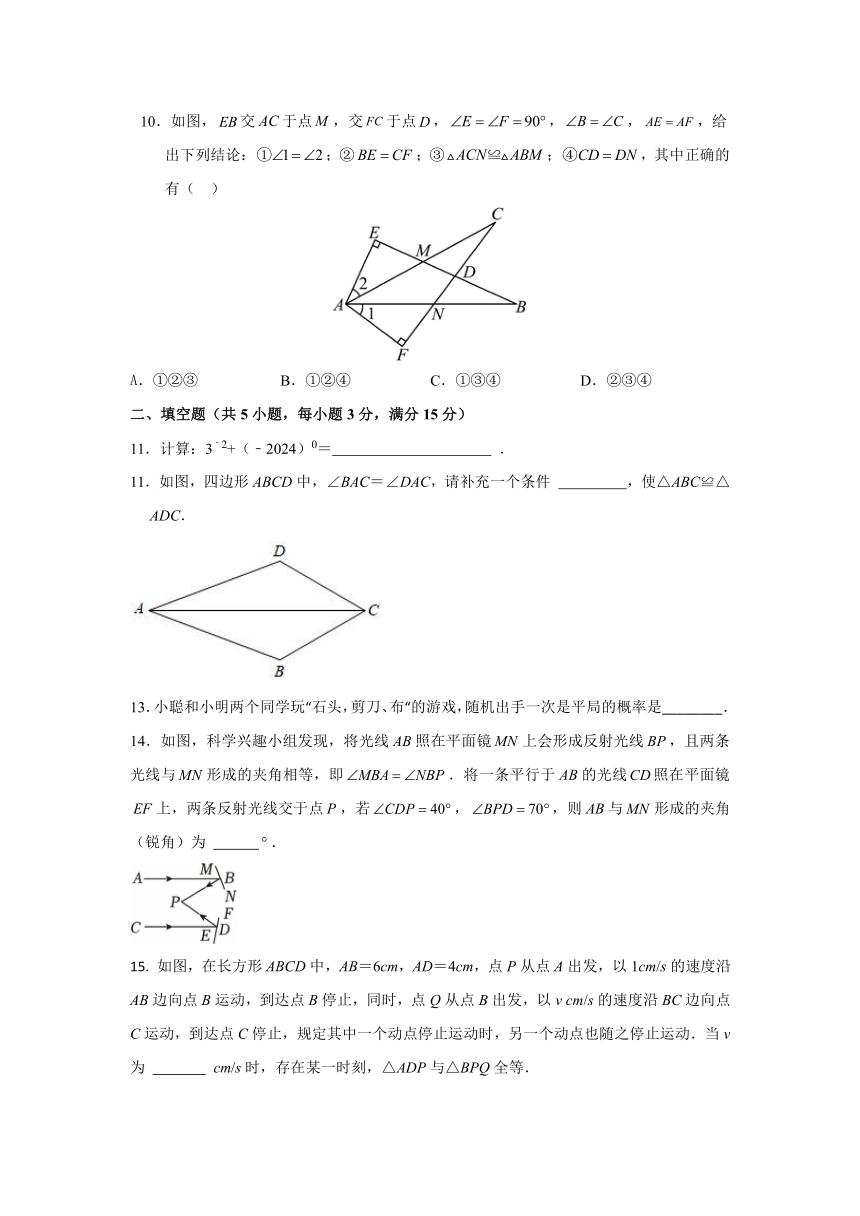
9.如图,将一张长方形纸片分别沿,折叠后,点落在点处,点落在点处,且,,三点刚好在同一条直线上,为的平分线.若,则的度数是
A. B. C. D.
10.如图,交于点,交于点,,,,给出下列结论:;②;③;,其中正确的有( )
①②③ B.①②④ C.①③④ D.②③④
二、填空题(共5小题,每小题3分,满分15分)
11.计算:3﹣2+(﹣2024)0= .
11.如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件 ,使△ABC≌△ADC.
13.小聪和小明两个同学玩“石头,剪刀、布“的游戏,随机出手一次是平局的概率是________.
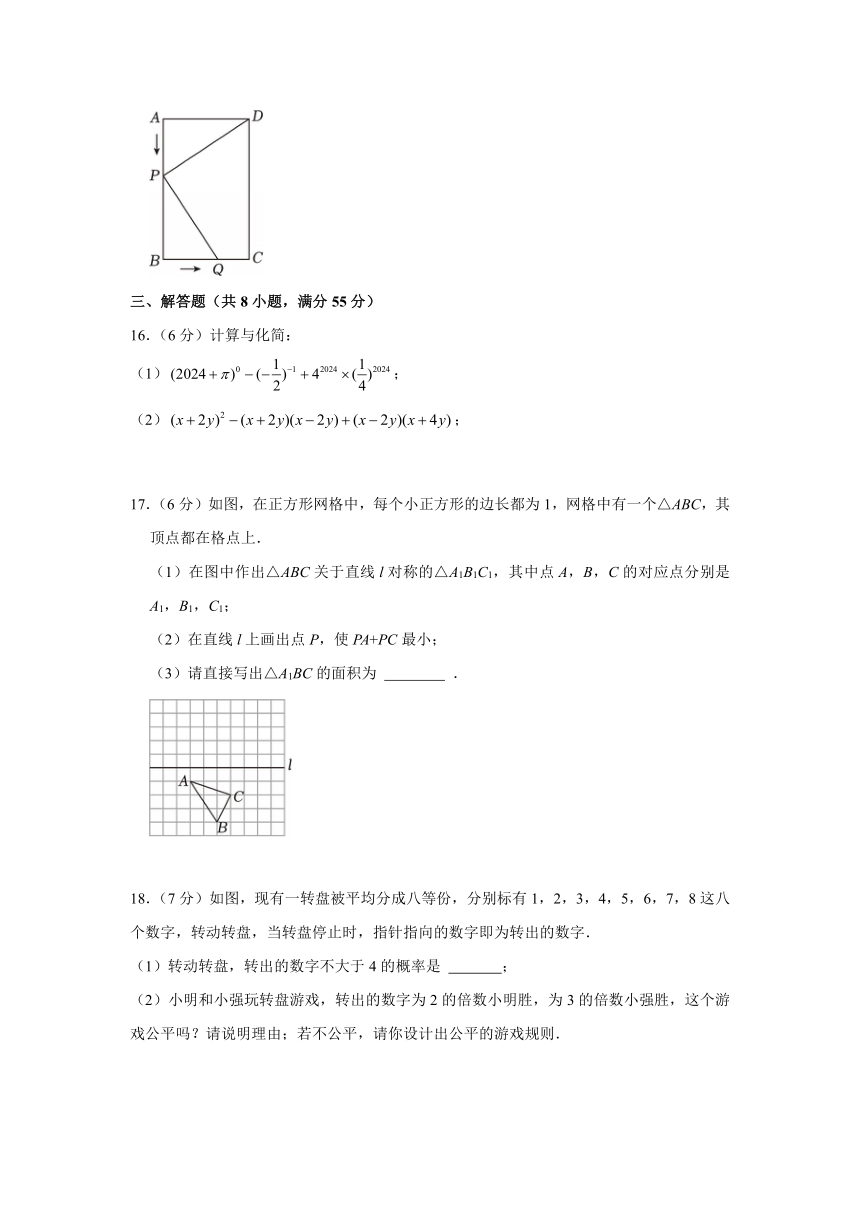
14.如图,科学兴趣小组发现,将光线照在平面镜上会形成反射光线,且两条光线与形成的夹角相等,即.将一条平行于的光线照在平面镜上,两条反射光线交于点,若,,则与形成的夹角(锐角)为 .
15. 如图,在长方形ABCD中,AB=6cm,AD=4cm,点P从点A出发,以1cm/s的速度沿AB边向点B运动,到达点B停止,同时,点Q从点B出发,以v cm/s的速度沿BC边向点C运动,到达点C停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v为 cm/s时,存在某一时刻,△ADP与△BPQ全等.
三、解答题(共8小题,满分55分)
16.(6分)计算与化简:
(1);
(2);
17.(6分)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个△ABC,其顶点都在格点上.
(1)在图中作出△ABC关于直线l对称的△A1B1C1,其中点A,B,C的对应点分别是A1,B1,C1;
(2)在直线l上画出点P,使PA+PC最小;
(3)请直接写出△A1BC的面积为 .
18.(7分)如图,现有一转盘被平均分成八等份,分别标有1,2,3,4,5,6,7,8这八个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1)转动转盘,转出的数字不大于4的概率是 ;
(2)小明和小强玩转盘游戏,转出的数字为2的倍数小明胜,为3的倍数小强胜,这个游戏公平吗?请说明理由;若不公平,请你设计出公平的游戏规则.
19.(7分)如图,四边形ABCD中,点E、F分别在AB、CD上,AD⊥AB,EF⊥AB,∠1+∠2=180°,G为CA延长线上一点,试说明∠DFE=∠DCB.
请将下面证明过程补充完整.
19.证明:∵AD⊥AB,EF⊥AB(已知),
∴∠EAD=∠BEF=90°( )
∴ ∥ (同位角相等,两直线平行)
∵∠1+∠2=180°(已知)
∠1+∠DAC=180°
∴∠2=∠DAC( )
∴AD∥BC( )
∴EF∥BC( )
∴∠DFE=∠DCB.( )
20.(7分)所谓完全平方式,就是对于一个整式,如果存在另一个整式,使,则称是完全平方式,例如:,.
(1)下列各式中是完全平方式的编号有 ;
①;②;③;④;⑤.
(2)若,请利用完全平方式求的值.
21.(9分)如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
22.(9分)某校五一期间组织学生去离学校100km的训练营开展研学活动.上午6:30,他们乘坐大巴从学校出发,行走半小时后,后勤老师携带物资乘坐轿车也从学校出发,沿大巴行走路线前往目的地,上午8:00,轿车在离学校60km的地方追上大巴并继续前行,又走了一段路程后,轿车因故障停留一段时间,故障解除后继续按原速前行,最后和大巴同时到达目的地,轿车和大巴离学校的路程s(km)与轿车所用时间x(h)的关系如图所示.(1)图中的A点表示的含义是 ,a的值为 ;
(2)求轿车故障持续的时间.
23.(12分)已知是等腰三角形,且,点是射线上的一动点,连接,以为腰在右侧作等腰,使,.
(1)如图1,当点在线段上时,求证:;
(2)如图2,当点在射线上运动时,取中点,连接,且.当为等腰三角形时,的度数为 ;
(3)如图3,当点在线段的延长线上,时,在线段上截取,使,并连接.求证:.
.
七年级(下)期末数学试卷2(北师大版)参考答案
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A D C C B B A
二、填空题
11.; 12. AD=AB(答案不唯一);13.;14.75;15.或1.
三、解答题
16.解:(1)
(2)
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,连接A1C,交直线l于点P,连接AP,
此时PA+PC=PA1+PC=A1C,为最小值,
则点P即为所求.
(3)△A1BC的面积为==.
故答案为:.
18.解:(1).
(2)转出的数字为2的倍的可能是2、4、6、8,即小明胜的概率为;转出的数字为3的倍的可能是3、6、即小强胜的概率为;由,故该游戏不公平;
设计的方案:转出数字是奇数,则小明胜,转出数字是偶数,则小强胜
19.故答案为:垂直的定义;AD;EF;同角的补角相等;内错角相等,两直线平行;平行于同一直线的两直线平行;两直线平行,同位角相等.
20.解:(1)①②④⑤;
(2),
,
.
21.将①②④作为题设,③作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:∠ABC=∠DEF.
证明:在△ABC和△DEF中
∵BE=CF
∴BC=EF
又∵AB=DE,AC=DF
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF.
将①③④作为题设,②作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF.
求证:AC=DF.
证明:在△ABC和△DEF中
∵BE=CF
∴BC=EF
又∵AB=DE,∠ABC=∠DEF
∴△ABC≌△DEF(SAS)
∴AC=DF.
22.解:(1)后勤老师携带物资乘坐轿车从学校出发时学生乘坐的大巴离学校的距离是20km;2;
(2)设轿车故障前离营地的路程s与所用时间x的函数表达式为s=kx(k≠0),
将点(1,60)代入,得:k=60,
∴轿车故障前离营地的路程s与所用时间x的函数表达式为s=60x,
当s=100时,,
此时2﹣=(h),
答:轿车故障持续的时间为.
23.(1)证明:,
,
即,
,,
,
;
(2)或或;
(3)证明:如图,延长到点,使得,连接,
,
,为等边三角形,
,
,
,,
,
,
,
,,
,,
,
,
,即
一、选择题(共10小题,每小题3分,满分30分)
1.下列数学经典图形中,其中是轴对称图形的是( )
A. B.
C. D.
2.计算的结果是
A. B. C. D.
3.下列说法正确的是( )
A.随意掷一枚均匀的硬币两次,至少有一次反面朝上
B.同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,两次点数之和为2是不可能事件
C.某同学在足球训练时,射门5次,射中4次,则可断定他射门命中的概率一定为80%
D.“从一副扑克牌中抽一张,恰好是大王”是随机事件
4.如图,在体育课上,李老师测量学生的跳远成绩的依据是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.过一点有且只有一条直线与已知直线垂直
5.阅读下列作图步骤:
①在OA和OB上分别截取OC,OD,使OC=OD;
②分别以C,D为圆心,以大于的长为半径作弧,两弧在∠AOB内交于点P;
③作射线OP,连接CP,DP,则△OCP≌△ODP的依据是( )
A.SAS B.AAS C.ASA D.SSS
6.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
A.20° B.30° C.35° D.50°
7.等腰三角形的周长是,其中一条边长为,则等腰三角形的腰长为
A. B.或 C. D.
8.声音在空气中的传播速度(简称声音速度)与空气温度的关系如下表:
空气温度/℃ ﹣20 ﹣10 0 10 20 30
声音速度/(m/s) 318 324 330 336 342
当空气温度为30℃时,声音在空气中的传播速度为( )
A.346m/s B.348m/s C.350m/s D.352m/s
9.如图,将一张长方形纸片分别沿,折叠后,点落在点处,点落在点处,且,,三点刚好在同一条直线上,为的平分线.若,则的度数是
A. B. C. D.
10.如图,交于点,交于点,,,,给出下列结论:;②;③;,其中正确的有( )
①②③ B.①②④ C.①③④ D.②③④
二、填空题(共5小题,每小题3分,满分15分)
11.计算:3﹣2+(﹣2024)0= .
11.如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件 ,使△ABC≌△ADC.
13.小聪和小明两个同学玩“石头,剪刀、布“的游戏,随机出手一次是平局的概率是________.
14.如图,科学兴趣小组发现,将光线照在平面镜上会形成反射光线,且两条光线与形成的夹角相等,即.将一条平行于的光线照在平面镜上,两条反射光线交于点,若,,则与形成的夹角(锐角)为 .
15. 如图,在长方形ABCD中,AB=6cm,AD=4cm,点P从点A出发,以1cm/s的速度沿AB边向点B运动,到达点B停止,同时,点Q从点B出发,以v cm/s的速度沿BC边向点C运动,到达点C停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v为 cm/s时,存在某一时刻,△ADP与△BPQ全等.
三、解答题(共8小题,满分55分)
16.(6分)计算与化简:
(1);
(2);
17.(6分)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个△ABC,其顶点都在格点上.
(1)在图中作出△ABC关于直线l对称的△A1B1C1,其中点A,B,C的对应点分别是A1,B1,C1;
(2)在直线l上画出点P,使PA+PC最小;
(3)请直接写出△A1BC的面积为 .
18.(7分)如图,现有一转盘被平均分成八等份,分别标有1,2,3,4,5,6,7,8这八个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1)转动转盘,转出的数字不大于4的概率是 ;
(2)小明和小强玩转盘游戏,转出的数字为2的倍数小明胜,为3的倍数小强胜,这个游戏公平吗?请说明理由;若不公平,请你设计出公平的游戏规则.
19.(7分)如图,四边形ABCD中,点E、F分别在AB、CD上,AD⊥AB,EF⊥AB,∠1+∠2=180°,G为CA延长线上一点,试说明∠DFE=∠DCB.
请将下面证明过程补充完整.
19.证明:∵AD⊥AB,EF⊥AB(已知),
∴∠EAD=∠BEF=90°( )
∴ ∥ (同位角相等,两直线平行)
∵∠1+∠2=180°(已知)
∠1+∠DAC=180°
∴∠2=∠DAC( )
∴AD∥BC( )
∴EF∥BC( )
∴∠DFE=∠DCB.( )
20.(7分)所谓完全平方式,就是对于一个整式,如果存在另一个整式,使,则称是完全平方式,例如:,.
(1)下列各式中是完全平方式的编号有 ;
①;②;③;④;⑤.
(2)若,请利用完全平方式求的值.
21.(9分)如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
22.(9分)某校五一期间组织学生去离学校100km的训练营开展研学活动.上午6:30,他们乘坐大巴从学校出发,行走半小时后,后勤老师携带物资乘坐轿车也从学校出发,沿大巴行走路线前往目的地,上午8:00,轿车在离学校60km的地方追上大巴并继续前行,又走了一段路程后,轿车因故障停留一段时间,故障解除后继续按原速前行,最后和大巴同时到达目的地,轿车和大巴离学校的路程s(km)与轿车所用时间x(h)的关系如图所示.(1)图中的A点表示的含义是 ,a的值为 ;
(2)求轿车故障持续的时间.
23.(12分)已知是等腰三角形,且,点是射线上的一动点,连接,以为腰在右侧作等腰,使,.
(1)如图1,当点在线段上时,求证:;
(2)如图2,当点在射线上运动时,取中点,连接,且.当为等腰三角形时,的度数为 ;
(3)如图3,当点在线段的延长线上,时,在线段上截取,使,并连接.求证:.
.
七年级(下)期末数学试卷2(北师大版)参考答案
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A D C C B B A
二、填空题
11.; 12. AD=AB(答案不唯一);13.;14.75;15.或1.
三、解答题
16.解:(1)
(2)
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,连接A1C,交直线l于点P,连接AP,
此时PA+PC=PA1+PC=A1C,为最小值,
则点P即为所求.
(3)△A1BC的面积为==.
故答案为:.
18.解:(1).
(2)转出的数字为2的倍的可能是2、4、6、8,即小明胜的概率为;转出的数字为3的倍的可能是3、6、即小强胜的概率为;由,故该游戏不公平;
设计的方案:转出数字是奇数,则小明胜,转出数字是偶数,则小强胜
19.故答案为:垂直的定义;AD;EF;同角的补角相等;内错角相等,两直线平行;平行于同一直线的两直线平行;两直线平行,同位角相等.
20.解:(1)①②④⑤;
(2),
,
.
21.将①②④作为题设,③作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:∠ABC=∠DEF.
证明:在△ABC和△DEF中
∵BE=CF
∴BC=EF
又∵AB=DE,AC=DF
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF.
将①③④作为题设,②作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF.
求证:AC=DF.
证明:在△ABC和△DEF中
∵BE=CF
∴BC=EF
又∵AB=DE,∠ABC=∠DEF
∴△ABC≌△DEF(SAS)
∴AC=DF.
22.解:(1)后勤老师携带物资乘坐轿车从学校出发时学生乘坐的大巴离学校的距离是20km;2;
(2)设轿车故障前离营地的路程s与所用时间x的函数表达式为s=kx(k≠0),
将点(1,60)代入,得:k=60,
∴轿车故障前离营地的路程s与所用时间x的函数表达式为s=60x,
当s=100时,,
此时2﹣=(h),
答:轿车故障持续的时间为.
23.(1)证明:,
,
即,
,,
,
;
(2)或或;
(3)证明:如图,延长到点,使得,连接,
,
,为等边三角形,
,
,
,,
,
,
,
,,
,,
,
,
,即
同课章节目录
