3.1代数式的概念 课件(共26张PPT) 北师大版(2024)数学七年级上册
文档属性
| 名称 | 3.1代数式的概念 课件(共26张PPT) 北师大版(2024)数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 07:51:50 | ||
图片预览






文档简介
(共26张PPT)
第3章 整式及其加减
1 代数式
第1课时 代数式的概念
北师版 七年级 数学(上)
导入新课
(1)若正方形的边长为a,则它的周长为____,面积为____;
(2)设n表示一个数,则它的相反数是_____;
(3)铅笔的单价是x元,4支铅笔要花_____元.
4a
a2
-n
4x
观察所列算式包含哪些运算,有何共同的运算特征.
思 考
在上节内容中出现过的4+3(x-1),x+x+(x+1),a+b,ab,2(m+n), , ,6(a-1)2等式子,有什么共同的特征?
探究新知
用字母表示图形的规律
问题1:用长度相同的小棒按下图所示的方式拼摆正方形。
…
(1) 按上面的方式,拼摆 2 个正方形需要____根小棒,拼摆 3 个正方形需要____根小棒;
(2) 拼摆 5 个这样的正方形需要____根小棒。
7
10
16
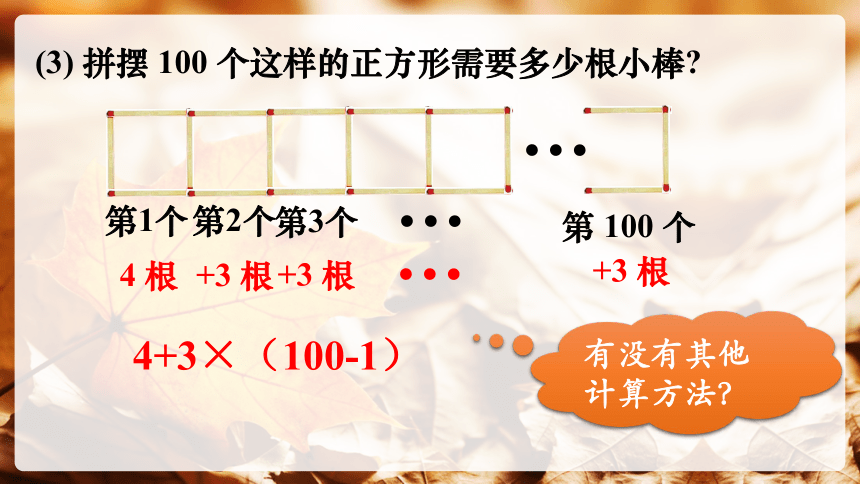
(3) 拼摆 100 个这样的正方形需要多少根小棒
第1个
4 根
第2个
第 100 个
+3 根
+3 根
…
有没有其他计算方法?
…
…
第3个
+3 根
4+3×(100-1)
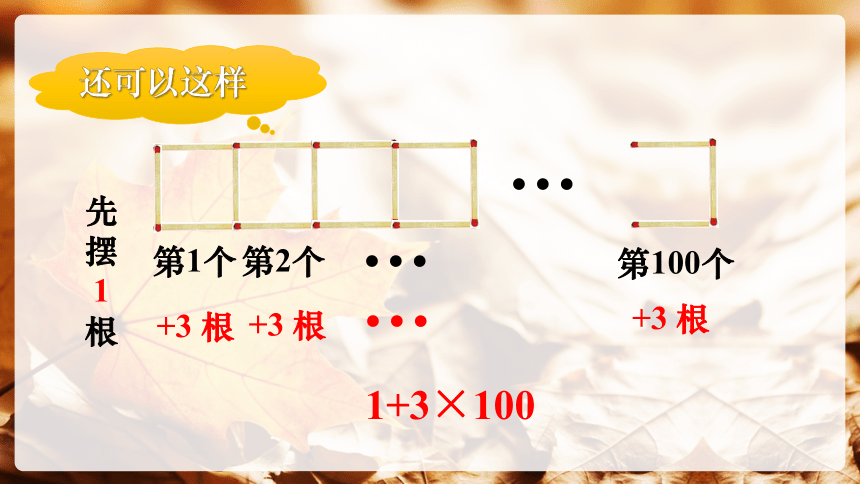
先摆 1根
第1个
+3 根
第100个
…
第2个
+3 根
+3 根
还可以这样
…
…
1+3×100
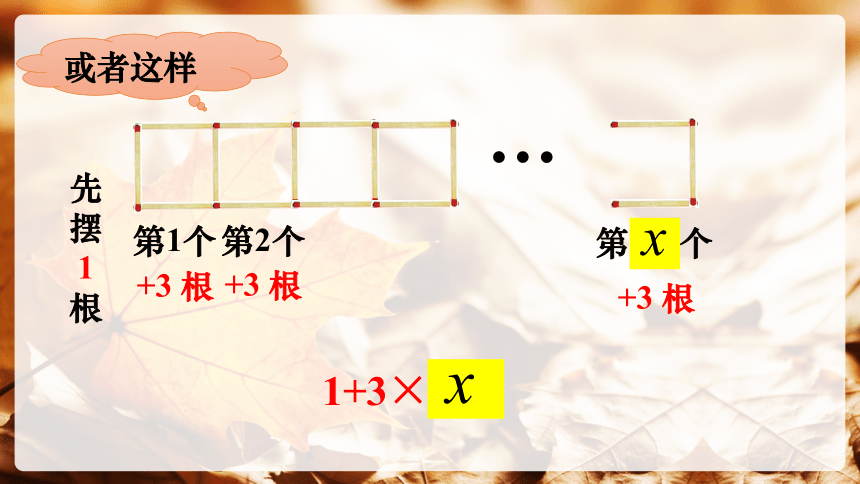
(4) 如果用 x 表示所搭正方形的个数, 那么拼摆 x 个这样的正方形需要多少根小棒?与同伴进行交流。
第1个
4 根
第2个
第100个
+3 根
+3 根
…
具体
一般
4+3×(100 -1)
…
第1个
+3 根
第100个
第2个
+3 根
+3 根
先摆 1根
或者这样
1+3×100
…
问题2:拼摆200个这样的正方形需要多少根小棒?
你是怎样计算的?
当x=200时,1+3x=1+3×200=601
即拼摆200个这样的正方形需要601根小棒。
在含有字母的式子中,可以用数值代替式子中的字母.
用字母表示数
问题3:在上面的活动中,我们借助字母描述了正方形的个数和小棒的根数之间的关系.你在以前的学习中有哪些地方用到了字母?这些字母都表示什么?
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) + c = a + (b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac + bc
1. 用字母表示数的运算律
2. 用字母表示有关图形的周长和面积计算公式
名称 图形 用字母表示公式 周长(C) 面积(S )
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
字母可以表示任何数.
代数式的概念
像这样4+3(x-1),x+x+(x+1),a+b,ab,2(m+n), , ,6(a-1)2由运算符号把数和字母连接而成的式子,叫做代数式。
注意:单独一个数或一个字母也是代数式,代数式不能带不等号或者等号.
(1)x与2的平方和; (2)x与2的和的平方; (3)x的平方与2的和.
用代数式表示数量关系时,一般要将句子分层,逐层分析,一步步列出代数式.
分析:这三题中都有关键词“平方”和“和”,但语序不一样,列出的代数式也不一样.
解:(1)x2+4;
(2)(x+2)2;
(3)x2+2.
归 纳
应用举例
【例1】用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为___________,面积为__________;
(2)一件衬衣的进价为a元,售价为2a元,则每件衬衣的利润为_____元;
(3)一个数的相反数为a,则这个数是______;
(4)甲、乙两地相距s km,一辆汽车每小时行驶75 km,则它从甲地到乙地的行驶时间为____h.
4+a
16+4a
a
-a
【例2】用字母表示阴影部分的面积.
【例3】下列代数式可以表示什么?
(1)2a-b; (2)2(a-b).
解:(1)2a与b的差或a的2倍与b的差;或用a表示一本作业本的价格,用b表示一只铅笔的价格,则2a-b表示买两本作业本比买一支铅笔多的钱数;
(2)2与a-b的积;或a与b的差的2倍.
课堂小结
代数式
用字母表示数
代数式
字母和数一样可以参与运算,可以用式子把 简明地表示出来
用运算符号把数和字母连接而成的式子
数量关系
根据实际问题列代数式
随堂练习
1.下列各式不是代数式的是( )
A.S=πR2 B.1 C. D.m+n
A
2.“x的2倍与y的 的和”用代数式表示为( )
B
3.国庆节期间,李老师一家四口开车去森林公园游玩,若门票每人a元,进入园区每辆车收费30元,李老师一家开一辆车进园区所需费用是________元.
(4a+30)
4.(1)一个两位数的个位数字是a,十位数字是b
(b≠0),请用代数式表示这个两位数;
(2)如何用代数式表示一个三位数?
解:(1)10b+a;
(2)若个位数字是a,十位数字是b,百位数字是c,则这个三位数为100c+10b+a.
5.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________.
n(n+2)
谢谢观看
第3章 整式及其加减
1 代数式
第1课时 代数式的概念
北师版 七年级 数学(上)
导入新课
(1)若正方形的边长为a,则它的周长为____,面积为____;
(2)设n表示一个数,则它的相反数是_____;
(3)铅笔的单价是x元,4支铅笔要花_____元.
4a
a2
-n
4x
观察所列算式包含哪些运算,有何共同的运算特征.
思 考
在上节内容中出现过的4+3(x-1),x+x+(x+1),a+b,ab,2(m+n), , ,6(a-1)2等式子,有什么共同的特征?
探究新知
用字母表示图形的规律
问题1:用长度相同的小棒按下图所示的方式拼摆正方形。
…
(1) 按上面的方式,拼摆 2 个正方形需要____根小棒,拼摆 3 个正方形需要____根小棒;
(2) 拼摆 5 个这样的正方形需要____根小棒。
7
10
16
(3) 拼摆 100 个这样的正方形需要多少根小棒
第1个
4 根
第2个
第 100 个
+3 根
+3 根
…
有没有其他计算方法?
…
…
第3个
+3 根
4+3×(100-1)
先摆 1根
第1个
+3 根
第100个
…
第2个
+3 根
+3 根
还可以这样
…
…
1+3×100
(4) 如果用 x 表示所搭正方形的个数, 那么拼摆 x 个这样的正方形需要多少根小棒?与同伴进行交流。
第1个
4 根
第2个
第100个
+3 根
+3 根
…
具体
一般
4+3×(100 -1)
…
第1个
+3 根
第100个
第2个
+3 根
+3 根
先摆 1根
或者这样
1+3×100
…
问题2:拼摆200个这样的正方形需要多少根小棒?
你是怎样计算的?
当x=200时,1+3x=1+3×200=601
即拼摆200个这样的正方形需要601根小棒。
在含有字母的式子中,可以用数值代替式子中的字母.
用字母表示数
问题3:在上面的活动中,我们借助字母描述了正方形的个数和小棒的根数之间的关系.你在以前的学习中有哪些地方用到了字母?这些字母都表示什么?
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) + c = a + (b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac + bc
1. 用字母表示数的运算律
2. 用字母表示有关图形的周长和面积计算公式
名称 图形 用字母表示公式 周长(C) 面积(S )
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
字母可以表示任何数.
代数式的概念
像这样4+3(x-1),x+x+(x+1),a+b,ab,2(m+n), , ,6(a-1)2由运算符号把数和字母连接而成的式子,叫做代数式。
注意:单独一个数或一个字母也是代数式,代数式不能带不等号或者等号.
(1)x与2的平方和; (2)x与2的和的平方; (3)x的平方与2的和.
用代数式表示数量关系时,一般要将句子分层,逐层分析,一步步列出代数式.
分析:这三题中都有关键词“平方”和“和”,但语序不一样,列出的代数式也不一样.
解:(1)x2+4;
(2)(x+2)2;
(3)x2+2.
归 纳
应用举例
【例1】用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为___________,面积为__________;
(2)一件衬衣的进价为a元,售价为2a元,则每件衬衣的利润为_____元;
(3)一个数的相反数为a,则这个数是______;
(4)甲、乙两地相距s km,一辆汽车每小时行驶75 km,则它从甲地到乙地的行驶时间为____h.
4+a
16+4a
a
-a
【例2】用字母表示阴影部分的面积.
【例3】下列代数式可以表示什么?
(1)2a-b; (2)2(a-b).
解:(1)2a与b的差或a的2倍与b的差;或用a表示一本作业本的价格,用b表示一只铅笔的价格,则2a-b表示买两本作业本比买一支铅笔多的钱数;
(2)2与a-b的积;或a与b的差的2倍.
课堂小结
代数式
用字母表示数
代数式
字母和数一样可以参与运算,可以用式子把 简明地表示出来
用运算符号把数和字母连接而成的式子
数量关系
根据实际问题列代数式
随堂练习
1.下列各式不是代数式的是( )
A.S=πR2 B.1 C. D.m+n
A
2.“x的2倍与y的 的和”用代数式表示为( )
B
3.国庆节期间,李老师一家四口开车去森林公园游玩,若门票每人a元,进入园区每辆车收费30元,李老师一家开一辆车进园区所需费用是________元.
(4a+30)
4.(1)一个两位数的个位数字是a,十位数字是b
(b≠0),请用代数式表示这个两位数;
(2)如何用代数式表示一个三位数?
解:(1)10b+a;
(2)若个位数字是a,十位数字是b,百位数字是c,则这个三位数为100c+10b+a.
5.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________.
n(n+2)
谢谢观看
同课章节目录
