1.5 三角函数的应用 九年级数学北师大版(2012)下册课后培优检测(含详解)
文档属性
| 名称 | 1.5 三角函数的应用 九年级数学北师大版(2012)下册课后培优检测(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 22:39:27 | ||
图片预览


文档简介
1.5 三角函数的应用——九年级数学北师大版(2012)下册课后培优检测
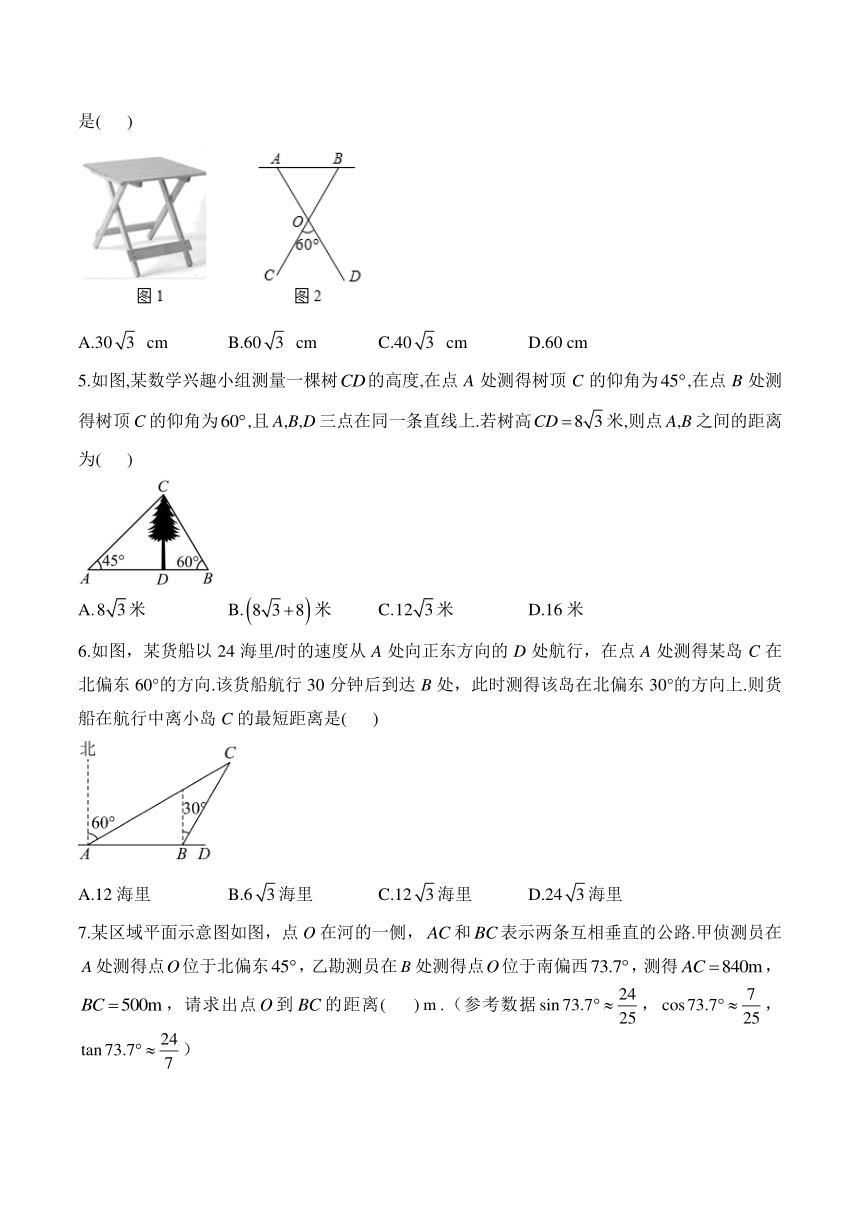
1.如图,某河堤横断面迎水坡的坡度为,则坡角( )
A. B. C. D.
2.如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆,,的最大仰角为.当时,则点A到桌面的最大高度是( )
A. B. C. D.
3.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,测得,,,则点A到的距离( )
A. B. C. D.
4.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
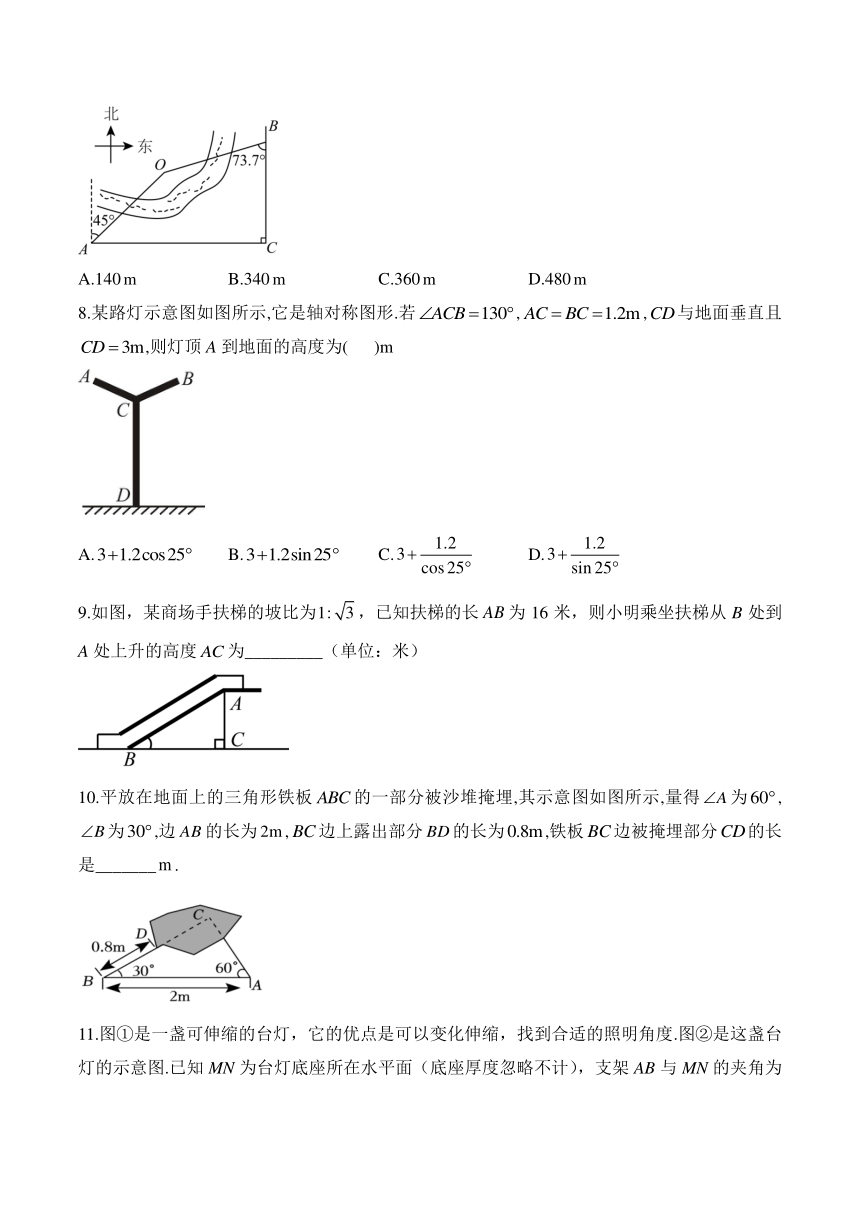
5.如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为,在点B处测得树顶C的仰角为,且A,B,D三点在同一条直线上.若树高米,则点A,B之间的距离为( )
A.米 B.米 C.米 D.16米
6.如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是( )
A.12海里 B.6海里 C.12海里 D.24海里
7.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
8.某路灯示意图如图所示,它是轴对称图形.若,,与地面垂直且,则灯顶A到地面的高度为( )m
A. B. C. D.
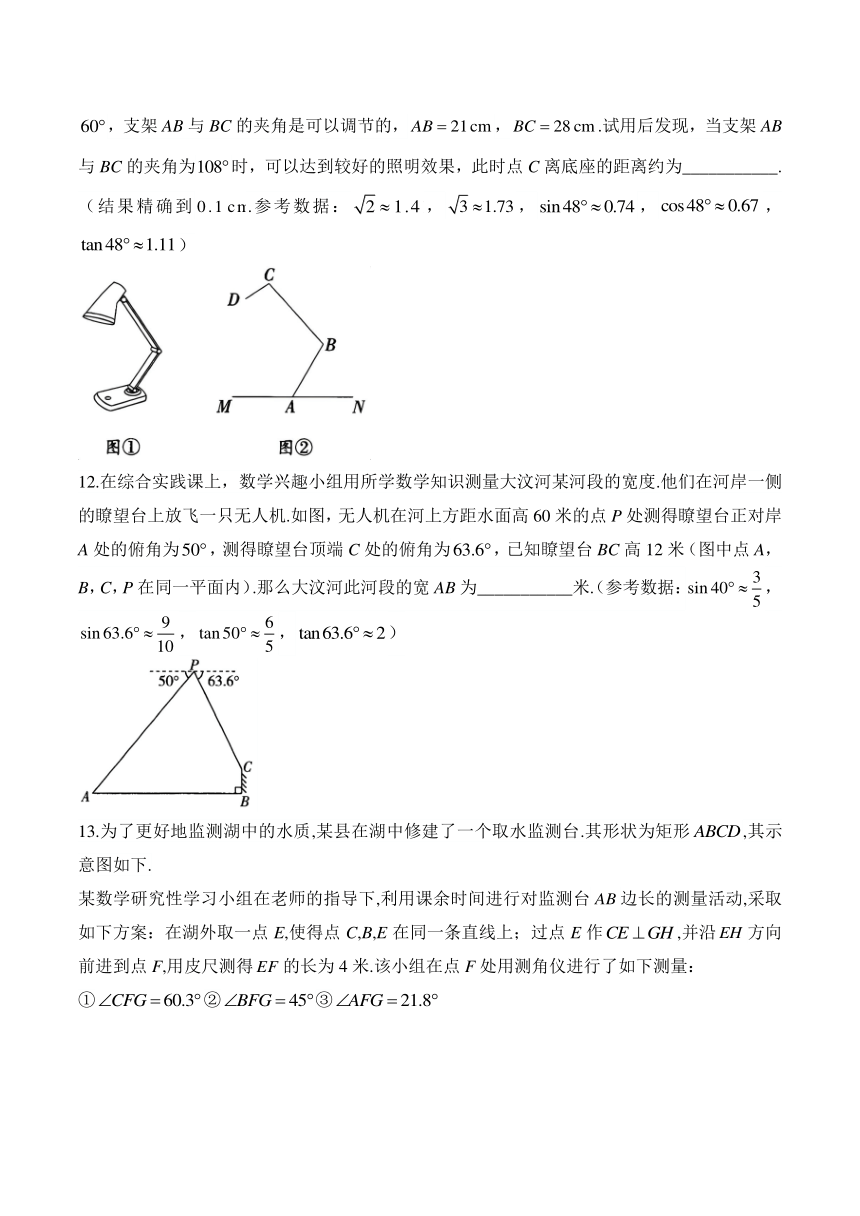
9.如图,某商场手扶梯的坡比为,已知扶梯的长为16米,则小明乘坐扶梯从B处到A处上升的高度为_________(单位:米)
10.平放在地面上的三角形铁板的一部分被沙堆掩埋,其示意图如图所示,量得为,为,边的长为,边上露出部分的长为,铁板边被掩埋部分的长是_______.
11.图①是一盏可伸缩的台灯,它的优点是可以变化伸缩,找到合适的照明角度.图②是这盏台灯的示意图.已知MN为台灯底座所在水平面(底座厚度忽略不计),支架AB与MN的夹角为,支架AB与BC的夹角是可以调节的,,.试用后发现,当支架AB与BC的夹角为时,可以达到较好的照明效果,此时点C离底座的距离约为___________.(结果精确到.参考数据:,,,,)
12.在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机.如图,无人机在河上方距水面高60米的点P处测得瞭望台正对岸A处的俯角为,测得瞭望台顶端C处的俯角为,已知瞭望台BC高12米(图中点A,B,C,P在同一平面内).那么大汶河此河段的宽AB为___________米.(参考数据:,,,)
13.为了更好地监测湖中的水质,某县在湖中修建了一个取水监测台.其形状为矩形,其示意图如下.
某数学研究性学习小组在老师的指导下,利用课余时间进行对监测台边长的测量活动,采取如下方案:在湖外取一点E,使得点C,B,E在同一条直线上;过点E作,并沿方向前进到点F,用皮尺测得的长为4米.该小组在点F处用测角仪进行了如下测量:
①②③
(1)为了计算边的长,在以上①②③中,应选择的条件是_____________;(填序号)
(2)在(1)的条件下,计算的长.(结果精确到.参考数据:,,,).
14.“五一”节期间,许多露营爱好者在我市某研学基地露营,为了遮阳和防雨,会搭建一种“天幕”,同学们想借此机会利用解直角三角形的知识,探究支杆角度大小与遮阳宽度的影响.
“天幕”截面示意图是轴对称图形,对称轴是垂直于地面的支杆,用绳子拉直后系在树干上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,,.
(1)天晴时打开“天幕”,若,求遮阳宽度(结果精确到);
(2)下雨时收拢“天幕”,从减少到,求点E下降的高度(结果精确到).
(参考数据:,,,)
答案以及解析
1.答案:A
解析:根据题意可知,
∴.
故选A.
2.答案:D
解析:如图,过点A作于F,过点B作于G,
在中,,
在中,,
点A到桌面的最大高度,
故选:D.
3.答案:A
解析:如下图所示,过点A作,
则的长度就是点A到的距离,,
在中,,
,,
,
.
故选:A.
4.答案:D
解析:如图,连接CD,过点O作交于点F,延长FO交AB于点E,
,∠COD=60°,
,为等边三角形,
∠COF=30°,
,
EF=2OF=60 cm,
即点A到地面的距离为60 cm.
故选:D.
5.答案:B
解析:由题意得:,,
在中,,
,
在中,,
,
,
米,
故选:B.
6.答案:B
解析:如图,过点C作,
由题意,得:,,,
在中,,
在中,,
,
;
故选:B.
7.答案:D
解析:作于,于,
则四边形为矩形,
,,
设,则,,
在中,,
,则,
在中,,
由题意得,,
解得,,
即点到的距离约为480,
故选:D.
8.答案:B
解析:如图,过点E作于点E,过点C作于点M,
所以,四边形是矩形,
∴,
∵路灯图是轴对称图形,且,
∵
在中,,
又
∴,
∴
即灯顶A到地面的高度为
故选:B.
9.答案:8
解析:∵扶梯的坡比为,
∴设米,则米,
∴,
解得,
∴米,
故答案为:8.
10.答案:
解析:由题意可知:三角形是直角三角形,则在直角三角形中,,
,
.
故答案为:.
11.答案:
解析:如图,过点C作于点E,过点B分别作于点F,于点G,则四边形EGBF是矩形,,.
在中,,,,.在中,,,,,点C离底座的距离约为.
12.答案:74
解析:如图,过点P作于点D,过点C作于点E,则四边形CBDE是矩形,,.由题意知,,,.在中,,,.在中,,,.故大汶河此河段的宽AB约为.
13.答案:(1)②③
(2)6米
解析:(1)由图形可知,要计算边的长,应选择的条件为②③;
故答案为:②③
(2)过点A作于点M,如图所示,由题意,可知:,.
在中,,
∴米,
在中,,
∴,
∴(米).
答:的长为6米.
14.答案:(1)
(2)
解析:由对称的性质可得,,,
在中,,,
∴,
∴;
(2)解析:如图,作于H,
,
∴,
∵,,
∴,
∴四边形为矩形,
∴,
在中,,
∴,
当时,,
当时,,
∴下雨时收拢“天幕”,从减少到,求点E下降的高度为.
1.如图,某河堤横断面迎水坡的坡度为,则坡角( )
A. B. C. D.
2.如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆,,的最大仰角为.当时,则点A到桌面的最大高度是( )
A. B. C. D.
3.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,测得,,,则点A到的距离( )
A. B. C. D.
4.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
5.如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为,在点B处测得树顶C的仰角为,且A,B,D三点在同一条直线上.若树高米,则点A,B之间的距离为( )
A.米 B.米 C.米 D.16米
6.如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是( )
A.12海里 B.6海里 C.12海里 D.24海里
7.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
8.某路灯示意图如图所示,它是轴对称图形.若,,与地面垂直且,则灯顶A到地面的高度为( )m
A. B. C. D.
9.如图,某商场手扶梯的坡比为,已知扶梯的长为16米,则小明乘坐扶梯从B处到A处上升的高度为_________(单位:米)
10.平放在地面上的三角形铁板的一部分被沙堆掩埋,其示意图如图所示,量得为,为,边的长为,边上露出部分的长为,铁板边被掩埋部分的长是_______.
11.图①是一盏可伸缩的台灯,它的优点是可以变化伸缩,找到合适的照明角度.图②是这盏台灯的示意图.已知MN为台灯底座所在水平面(底座厚度忽略不计),支架AB与MN的夹角为,支架AB与BC的夹角是可以调节的,,.试用后发现,当支架AB与BC的夹角为时,可以达到较好的照明效果,此时点C离底座的距离约为___________.(结果精确到.参考数据:,,,,)
12.在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机.如图,无人机在河上方距水面高60米的点P处测得瞭望台正对岸A处的俯角为,测得瞭望台顶端C处的俯角为,已知瞭望台BC高12米(图中点A,B,C,P在同一平面内).那么大汶河此河段的宽AB为___________米.(参考数据:,,,)
13.为了更好地监测湖中的水质,某县在湖中修建了一个取水监测台.其形状为矩形,其示意图如下.
某数学研究性学习小组在老师的指导下,利用课余时间进行对监测台边长的测量活动,采取如下方案:在湖外取一点E,使得点C,B,E在同一条直线上;过点E作,并沿方向前进到点F,用皮尺测得的长为4米.该小组在点F处用测角仪进行了如下测量:
①②③
(1)为了计算边的长,在以上①②③中,应选择的条件是_____________;(填序号)
(2)在(1)的条件下,计算的长.(结果精确到.参考数据:,,,).
14.“五一”节期间,许多露营爱好者在我市某研学基地露营,为了遮阳和防雨,会搭建一种“天幕”,同学们想借此机会利用解直角三角形的知识,探究支杆角度大小与遮阳宽度的影响.
“天幕”截面示意图是轴对称图形,对称轴是垂直于地面的支杆,用绳子拉直后系在树干上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,,.
(1)天晴时打开“天幕”,若,求遮阳宽度(结果精确到);
(2)下雨时收拢“天幕”,从减少到,求点E下降的高度(结果精确到).
(参考数据:,,,)
答案以及解析
1.答案:A
解析:根据题意可知,
∴.
故选A.
2.答案:D
解析:如图,过点A作于F,过点B作于G,
在中,,
在中,,
点A到桌面的最大高度,
故选:D.
3.答案:A
解析:如下图所示,过点A作,
则的长度就是点A到的距离,,
在中,,
,,
,
.
故选:A.
4.答案:D
解析:如图,连接CD,过点O作交于点F,延长FO交AB于点E,
,∠COD=60°,
,为等边三角形,
∠COF=30°,
,
EF=2OF=60 cm,
即点A到地面的距离为60 cm.
故选:D.
5.答案:B
解析:由题意得:,,
在中,,
,
在中,,
,
,
米,
故选:B.
6.答案:B
解析:如图,过点C作,
由题意,得:,,,
在中,,
在中,,
,
;
故选:B.
7.答案:D
解析:作于,于,
则四边形为矩形,
,,
设,则,,
在中,,
,则,
在中,,
由题意得,,
解得,,
即点到的距离约为480,
故选:D.
8.答案:B
解析:如图,过点E作于点E,过点C作于点M,
所以,四边形是矩形,
∴,
∵路灯图是轴对称图形,且,
∵
在中,,
又
∴,
∴
即灯顶A到地面的高度为
故选:B.
9.答案:8
解析:∵扶梯的坡比为,
∴设米,则米,
∴,
解得,
∴米,
故答案为:8.
10.答案:
解析:由题意可知:三角形是直角三角形,则在直角三角形中,,
,
.
故答案为:.
11.答案:
解析:如图,过点C作于点E,过点B分别作于点F,于点G,则四边形EGBF是矩形,,.
在中,,,,.在中,,,,,点C离底座的距离约为.
12.答案:74
解析:如图,过点P作于点D,过点C作于点E,则四边形CBDE是矩形,,.由题意知,,,.在中,,,.在中,,,.故大汶河此河段的宽AB约为.
13.答案:(1)②③
(2)6米
解析:(1)由图形可知,要计算边的长,应选择的条件为②③;
故答案为:②③
(2)过点A作于点M,如图所示,由题意,可知:,.
在中,,
∴米,
在中,,
∴,
∴(米).
答:的长为6米.
14.答案:(1)
(2)
解析:由对称的性质可得,,,
在中,,,
∴,
∴;
(2)解析:如图,作于H,
,
∴,
∵,,
∴,
∴四边形为矩形,
∴,
在中,,
∴,
当时,,
当时,,
∴下雨时收拢“天幕”,从减少到,求点E下降的高度为.
