26.3 实践与探索(含详解)九年级数学华东师大版(2012)下册课后培优检测
文档属性
| 名称 | 26.3 实践与探索(含详解)九年级数学华东师大版(2012)下册课后培优检测 | 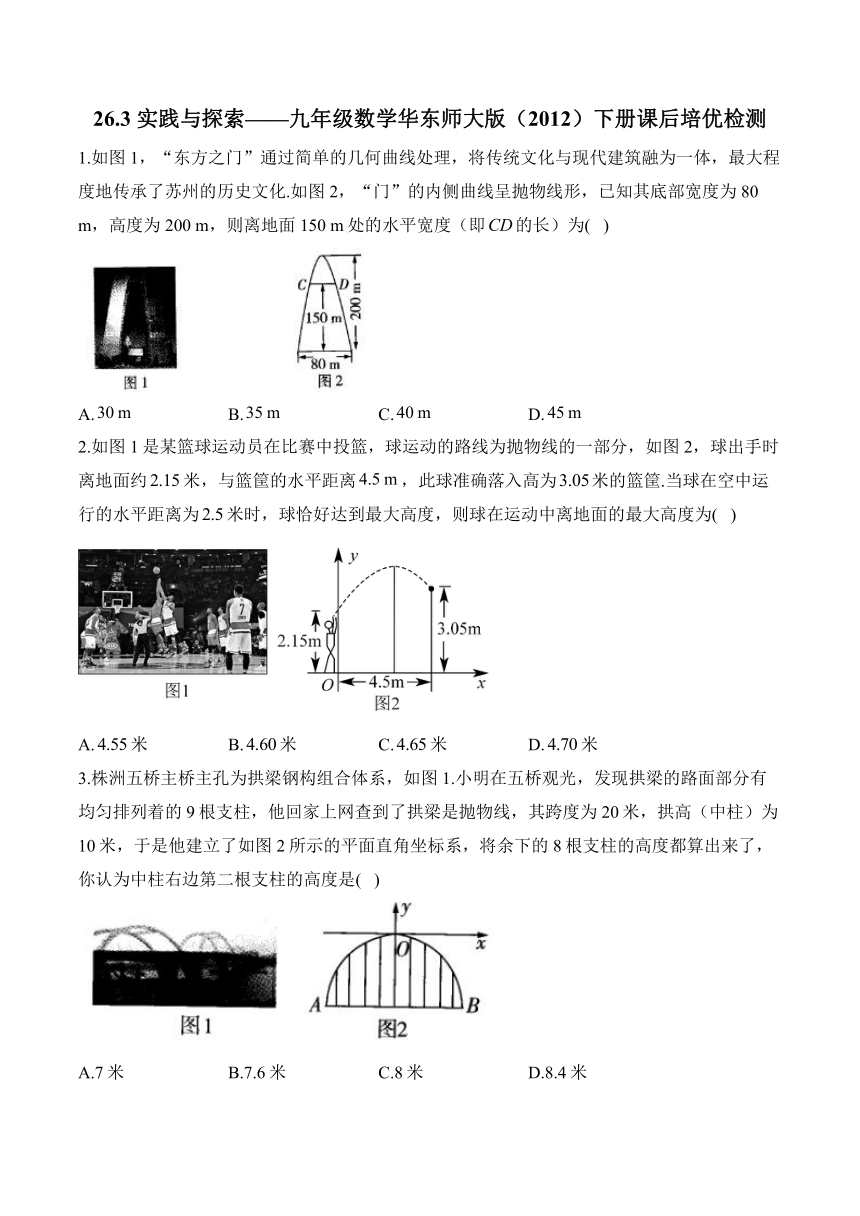 | |
| 格式 | docx | ||
| 文件大小 | 542.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 21:56:27 | ||
图片预览


文档简介
26.3 实践与探索——九年级数学华东师大版(2012)下册课后培优检测
1.如图1,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图2,“门”的内侧曲线呈抛物线形,已知其底部宽度为80 m,高度为200 m,则离地面150 m处的水平宽度(即的长)为( )
A. B. C. D.
2.如图1是某篮球运动员在比赛中投篮,球运动的路线为抛物线的一部分,如图2,球出手时离地面约米,与篮筐的水平距离,此球准确落入高为米的篮筐.当球在空中运行的水平距离为米时,球恰好达到最大高度,则球在运动中离地面的最大高度为( )
A.米 B.米 C.米 D.米
3.株洲五桥主桥主孔为拱梁钢构组合体系,如图1.小明在五桥观光,发现拱梁的路面部分有均匀排列着的9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)为10米,于是他建立了如图2所示的平面直角坐标系,将余下的8根支柱的高度都算出来了,你认为中柱右边第二根支柱的高度是( )
A.7米 B.7.6米 C.8米 D.8.4米
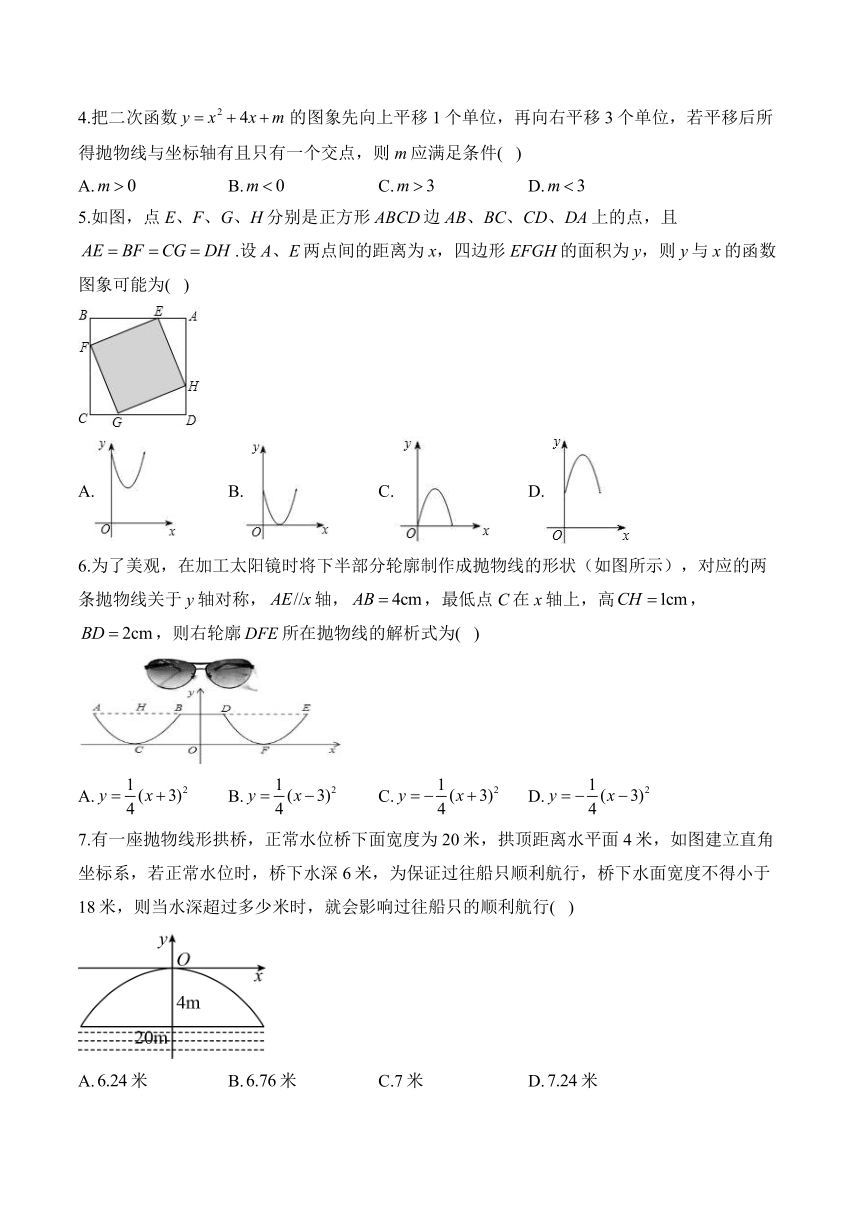
4.把二次函数的图象先向上平移1个单位,再向右平移3个单位,若平移后所得抛物线与坐标轴有且只有一个交点,则m应满足条件( )
A. B. C. D.
5.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A. B. C. D.
6.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,轴,,最低点C在x轴上,高,,则右轮廓所在抛物线的解析式为( )
A. B. C. D.
7.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A.米 B.米 C.7米 D.米
8.如图所示,是一个长、宽的矩形花园,根据需要将它的长缩短、宽增加,要想使修改后的花园面积达到最大,则x应为( )
A.1 B. C.2 D.4
9.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是,那么飞机着陆后滑行______s才能停下来.
10.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售单价定为_________元时,才能使每天所获销售利润最大.
11.如图,要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心,水管长度应为__________.
12.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m.若要使得建成的饲养室面积最大,则利用墙体的长度为__________m.
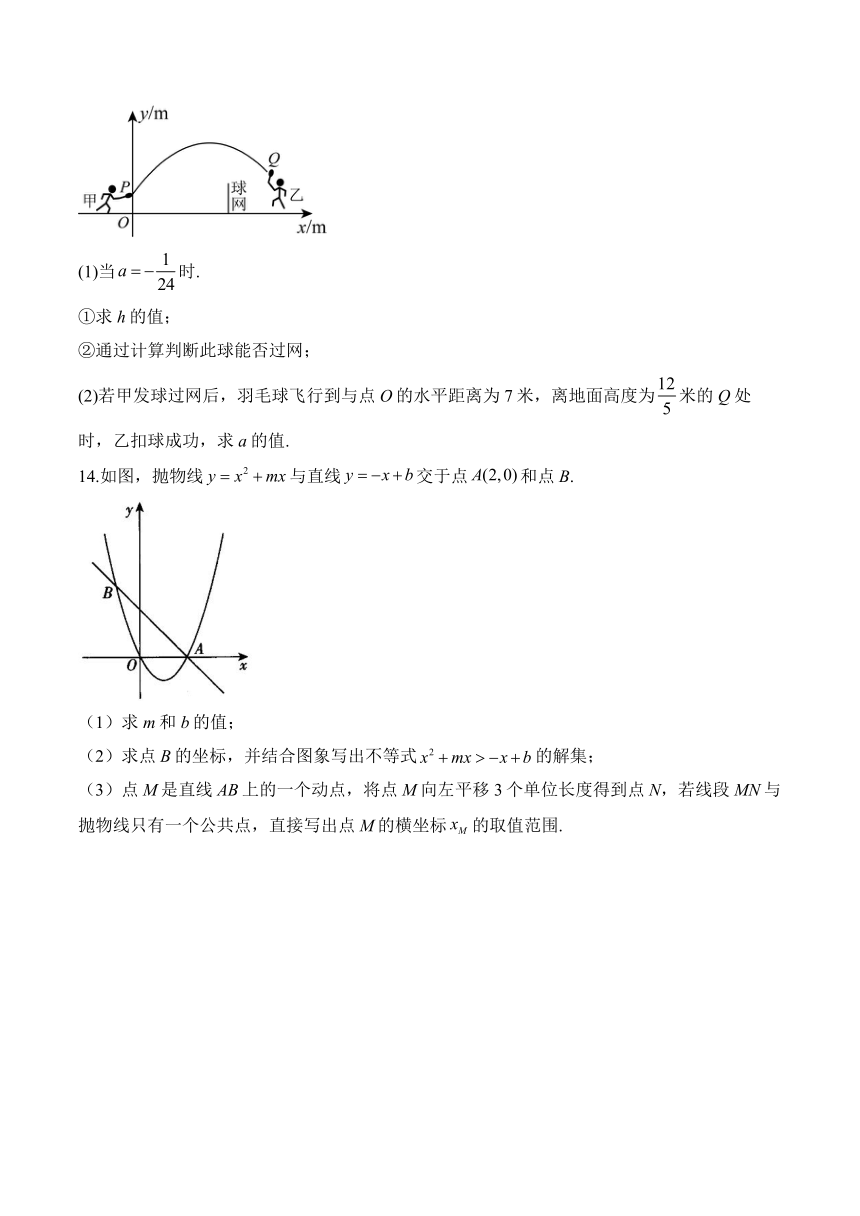
13.嘉琪同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛技术进行技术分析,下面是他对某次击球线路的分析.甲、乙两人进行羽毛球比赛,羽毛球飞行的线路为抛物线的一部分,如图,甲在点O正上方的点P处发出一球,羽毛球飞行的高度y(米)与水平距离x(米)之间满足函数关系式.已知点O与球网的水平距离为5米,球网的高度为1.5米.
(1)当时.
①求h的值;
②通过计算判断此球能否过网;
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7米,离地面高度为米的Q处时,乙扣球成功,求a的值.
14.如图,抛物线与直线交于点和点B.
(1)求m和b的值;
(2)求点B的坐标,并结合图象写出不等式的解集;
(3)点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.
答案以及解析
1.答案:C
解析:如图,建立平面直角坐标系,易得,,.设抛物线的表达式为,将代入,得,解得,抛物线的表达式为.将代入,得,解得,,,.
2.答案:C
解析:根据题意得:抛物线过点和,对称轴为直线,
设抛物线解析式为,
把和代入解析式得:,
解得,
抛物线解析式为,
,
函数的最大值为,
球在运动中离地面的最大高度为,
故选:C.
3.答案:D
解析:根据题意可得点B的坐标是,设抛物线对应的二次函数的表达式为,将点的坐标代入,得,解得,所以该抛物线对应的函数表达式为.可设中柱右边第二根支柱上端点的坐标为,于是,所以中柱右边第二根支柱的高度是(米).
4.答案:C
解析:,则平移后所得抛物线的表达式为.平移后所得抛物线与坐标轴有且只有一个交点,平移后所得抛物线与x轴没有交点,,解得.
5.答案:A
解析:由题意知四边形EFGH为正方形.设正方形的边长为m,则,,,,,,,.故选A.
6.答案:B
解析:高cm,cm,且B、D关于y轴对称,
D点坐标为,
轴,cm,最低点C在x轴上,
关于直线CH对称,
左边抛物线的顶点C的坐标为,
右边抛物线的顶点F的坐标为,
设右边抛物线的解析式为,
把代入得,解得,
右边抛物线的解析式为,
故选:B.
7.答案:B
解析:根据题意可得:
该抛物线经过,,
设抛物线解析式为,
把代入得:,
解得:,
该抛物线解析式为,
把代入得:,
此时水深为:(米),
故选:B.
8.答案:C
解析:由题意得修改后的花园面积
,
,
当时,修改后的花园面积达到最大,
故选:C.
9.答案:
解析:∵,,
∴当时,s有最大值,
∴飞机着陆后滑行才能停下来,
故答案为:.
10.答案:11
解析:设销售单价定为x元(),每天所获利润为y元,则,所以将销售单价定为11元时,才能使每天所获销售利润最大,故答案为11.
11.答案:
解析:以池的中心为原点,竖直安装的水管为y轴,与水管垂直的水平线为x轴建立平面直角坐标系.因为在距池中心的水平距离为处达到最高,高度为,所以设抛物线的表达式为,将代入,得,所以该抛物线的表达式为.令,则,故水管长度为.
12.答案:14
解析:设平行于墙的一边长为x m,则垂直于墙的一边长为m,总面积,当时,建成的饲养室面积最大.故答案为14.
13.答案:(1)①,②此球能过网
(2)
解析:(1)①由题意得,当时,
则
将代入得
解得,
②∵
∴当时,
∵
∴此球能过网;
(2)将,,代入,
得,
解得
∴.
14、
(1)答案:,
解析:抛物线经过点,
,
.
直线经过点,
,
.
(2)答案:或
解析:当时,,,
点B的坐标为.
结合题中图象可知,不等式的解集为或.
(3)答案:或
解析:将直线向左平移3个单位得到直线l,易知直线l的表达式为.令,整理,得,易知该方程没有实数根,故直线l与抛物线没有公共点,如图.易知抛物线的顶点坐标为,过点作x轴的平行线,交直线于点C.当点M在线段上(不与点A重合)时,线段与抛物线只有一个公共点,此时.当点M在线段上(不与点C重合)时,线段与抛物线有两个公共点.当点M与点C重合时,线段与抛物线只有一个公共点,此时,代入,得.综上可知,点M的横坐标的取值范围为或.
1.如图1,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图2,“门”的内侧曲线呈抛物线形,已知其底部宽度为80 m,高度为200 m,则离地面150 m处的水平宽度(即的长)为( )
A. B. C. D.
2.如图1是某篮球运动员在比赛中投篮,球运动的路线为抛物线的一部分,如图2,球出手时离地面约米,与篮筐的水平距离,此球准确落入高为米的篮筐.当球在空中运行的水平距离为米时,球恰好达到最大高度,则球在运动中离地面的最大高度为( )
A.米 B.米 C.米 D.米
3.株洲五桥主桥主孔为拱梁钢构组合体系,如图1.小明在五桥观光,发现拱梁的路面部分有均匀排列着的9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)为10米,于是他建立了如图2所示的平面直角坐标系,将余下的8根支柱的高度都算出来了,你认为中柱右边第二根支柱的高度是( )
A.7米 B.7.6米 C.8米 D.8.4米
4.把二次函数的图象先向上平移1个单位,再向右平移3个单位,若平移后所得抛物线与坐标轴有且只有一个交点,则m应满足条件( )
A. B. C. D.
5.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A. B. C. D.
6.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,轴,,最低点C在x轴上,高,,则右轮廓所在抛物线的解析式为( )
A. B. C. D.
7.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A.米 B.米 C.7米 D.米
8.如图所示,是一个长、宽的矩形花园,根据需要将它的长缩短、宽增加,要想使修改后的花园面积达到最大,则x应为( )
A.1 B. C.2 D.4
9.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是,那么飞机着陆后滑行______s才能停下来.
10.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售单价定为_________元时,才能使每天所获销售利润最大.
11.如图,要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心,水管长度应为__________.
12.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m.若要使得建成的饲养室面积最大,则利用墙体的长度为__________m.
13.嘉琪同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛技术进行技术分析,下面是他对某次击球线路的分析.甲、乙两人进行羽毛球比赛,羽毛球飞行的线路为抛物线的一部分,如图,甲在点O正上方的点P处发出一球,羽毛球飞行的高度y(米)与水平距离x(米)之间满足函数关系式.已知点O与球网的水平距离为5米,球网的高度为1.5米.
(1)当时.
①求h的值;
②通过计算判断此球能否过网;
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7米,离地面高度为米的Q处时,乙扣球成功,求a的值.
14.如图,抛物线与直线交于点和点B.
(1)求m和b的值;
(2)求点B的坐标,并结合图象写出不等式的解集;
(3)点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.
答案以及解析
1.答案:C
解析:如图,建立平面直角坐标系,易得,,.设抛物线的表达式为,将代入,得,解得,抛物线的表达式为.将代入,得,解得,,,.
2.答案:C
解析:根据题意得:抛物线过点和,对称轴为直线,
设抛物线解析式为,
把和代入解析式得:,
解得,
抛物线解析式为,
,
函数的最大值为,
球在运动中离地面的最大高度为,
故选:C.
3.答案:D
解析:根据题意可得点B的坐标是,设抛物线对应的二次函数的表达式为,将点的坐标代入,得,解得,所以该抛物线对应的函数表达式为.可设中柱右边第二根支柱上端点的坐标为,于是,所以中柱右边第二根支柱的高度是(米).
4.答案:C
解析:,则平移后所得抛物线的表达式为.平移后所得抛物线与坐标轴有且只有一个交点,平移后所得抛物线与x轴没有交点,,解得.
5.答案:A
解析:由题意知四边形EFGH为正方形.设正方形的边长为m,则,,,,,,,.故选A.
6.答案:B
解析:高cm,cm,且B、D关于y轴对称,
D点坐标为,
轴,cm,最低点C在x轴上,
关于直线CH对称,
左边抛物线的顶点C的坐标为,
右边抛物线的顶点F的坐标为,
设右边抛物线的解析式为,
把代入得,解得,
右边抛物线的解析式为,
故选:B.
7.答案:B
解析:根据题意可得:
该抛物线经过,,
设抛物线解析式为,
把代入得:,
解得:,
该抛物线解析式为,
把代入得:,
此时水深为:(米),
故选:B.
8.答案:C
解析:由题意得修改后的花园面积
,
,
当时,修改后的花园面积达到最大,
故选:C.
9.答案:
解析:∵,,
∴当时,s有最大值,
∴飞机着陆后滑行才能停下来,
故答案为:.
10.答案:11
解析:设销售单价定为x元(),每天所获利润为y元,则,所以将销售单价定为11元时,才能使每天所获销售利润最大,故答案为11.
11.答案:
解析:以池的中心为原点,竖直安装的水管为y轴,与水管垂直的水平线为x轴建立平面直角坐标系.因为在距池中心的水平距离为处达到最高,高度为,所以设抛物线的表达式为,将代入,得,所以该抛物线的表达式为.令,则,故水管长度为.
12.答案:14
解析:设平行于墙的一边长为x m,则垂直于墙的一边长为m,总面积,当时,建成的饲养室面积最大.故答案为14.
13.答案:(1)①,②此球能过网
(2)
解析:(1)①由题意得,当时,
则
将代入得
解得,
②∵
∴当时,
∵
∴此球能过网;
(2)将,,代入,
得,
解得
∴.
14、
(1)答案:,
解析:抛物线经过点,
,
.
直线经过点,
,
.
(2)答案:或
解析:当时,,,
点B的坐标为.
结合题中图象可知,不等式的解集为或.
(3)答案:或
解析:将直线向左平移3个单位得到直线l,易知直线l的表达式为.令,整理,得,易知该方程没有实数根,故直线l与抛物线没有公共点,如图.易知抛物线的顶点坐标为,过点作x轴的平行线,交直线于点C.当点M在线段上(不与点A重合)时,线段与抛物线只有一个公共点,此时.当点M在线段上(不与点C重合)时,线段与抛物线有两个公共点.当点M与点C重合时,线段与抛物线只有一个公共点,此时,代入,得.综上可知,点M的横坐标的取值范围为或.
