27.4 正多边形和圆(含详解)九年级数学华东师大版(2012)下册课后培优检测
文档属性
| 名称 | 27.4 正多边形和圆(含详解)九年级数学华东师大版(2012)下册课后培优检测 | 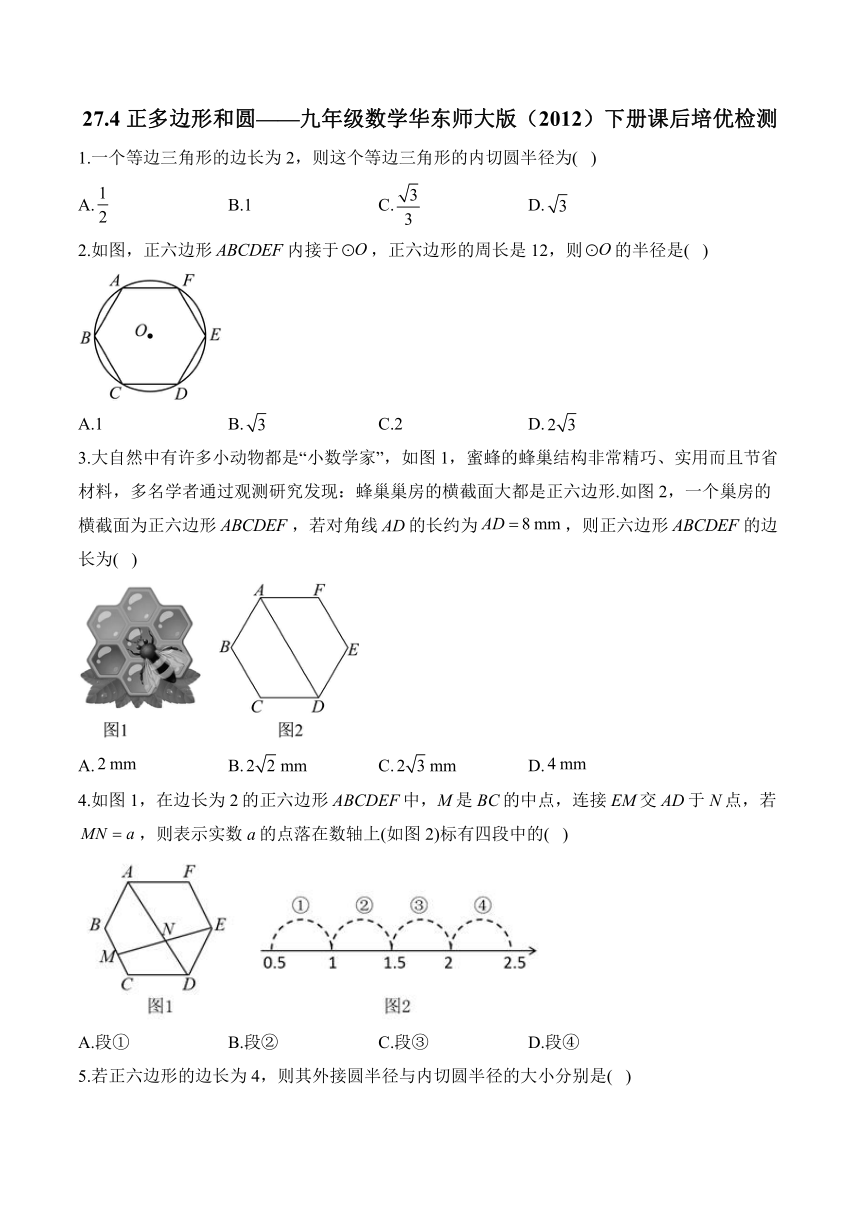 | |
| 格式 | docx | ||
| 文件大小 | 973.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 21:57:09 | ||
图片预览


文档简介
27.4 正多边形和圆——九年级数学华东师大版(2012)下册课后培优检测
1.一个等边三角形的边长为2,则这个等边三角形的内切圆半径为( )
A. B.1 C. D.
2.如图,正六边形内接于,正六边形的周长是12,则的半径是( )
A.1 B. C.2 D.
3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
4.如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若,则表示实数a的点落在数轴上(如图2)标有四段中的( )
A.段① B.段② C.段③ D.段④
5.若正六边形的边长为4,则其外接圆半径与内切圆半径的大小分别是( )
A.4, B.4,2 C.,2 D.,
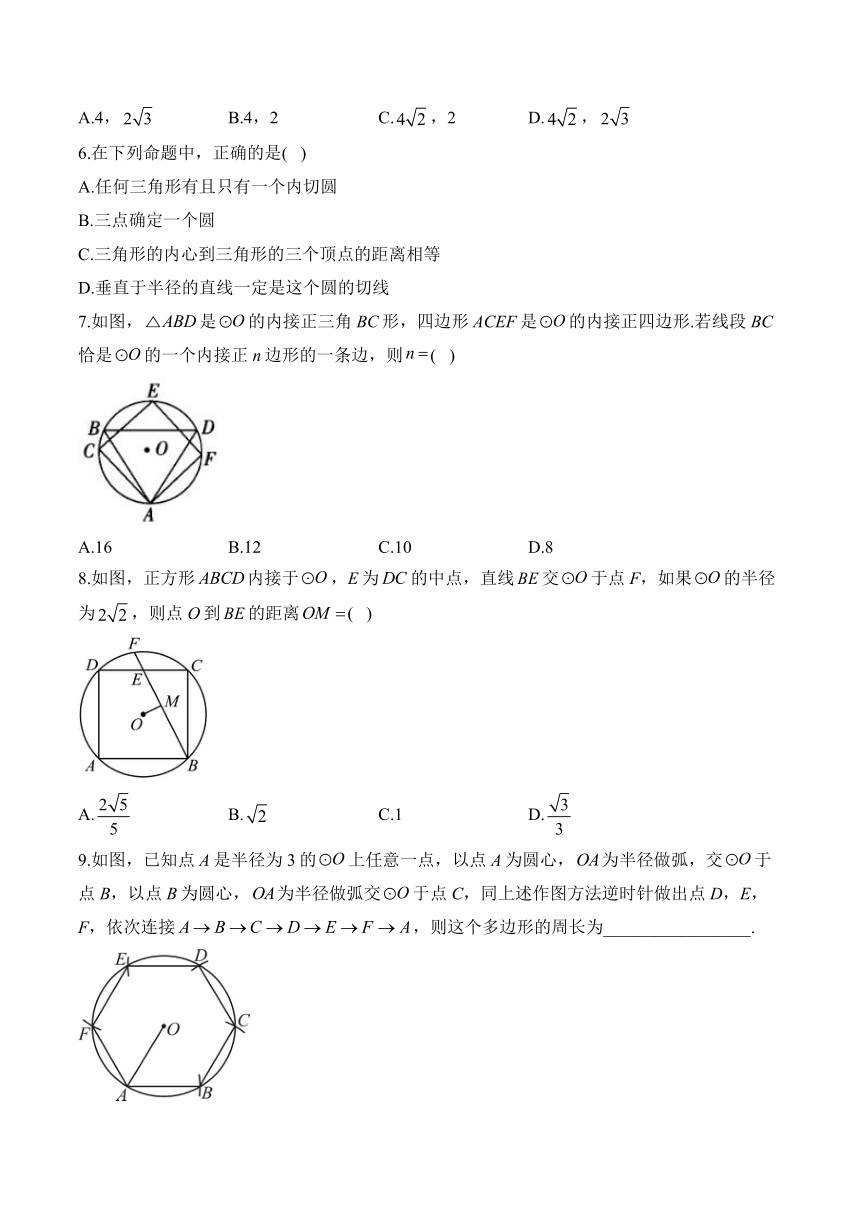
6.在下列命题中,正确的是( )
A.任何三角形有且只有一个内切圆
B.三点确定一个圆
C.三角形的内心到三角形的三个顶点的距离相等
D.垂直于半径的直线一定是这个圆的切线
7.如图,是的内接正三角BC形,四边形ACEF是的内接正四边形.若线段BC恰是的一个内接正n边形的一条边,则( )
A.16 B.12 C.10 D.8
8.如图,正方形内接于,E为的中点,直线交于点F,如果的半径为,则点O到的距离( )
A. B. C.1 D.
9.如图,已知点A是半径为3的上任意一点,以点A为圆心,为半径做弧,交于点B,以点B为圆心,为半径做弧交于点C,同上述作图方法逆时针做出点D,E,F,依次连接,则这个多边形的周长为_________________.
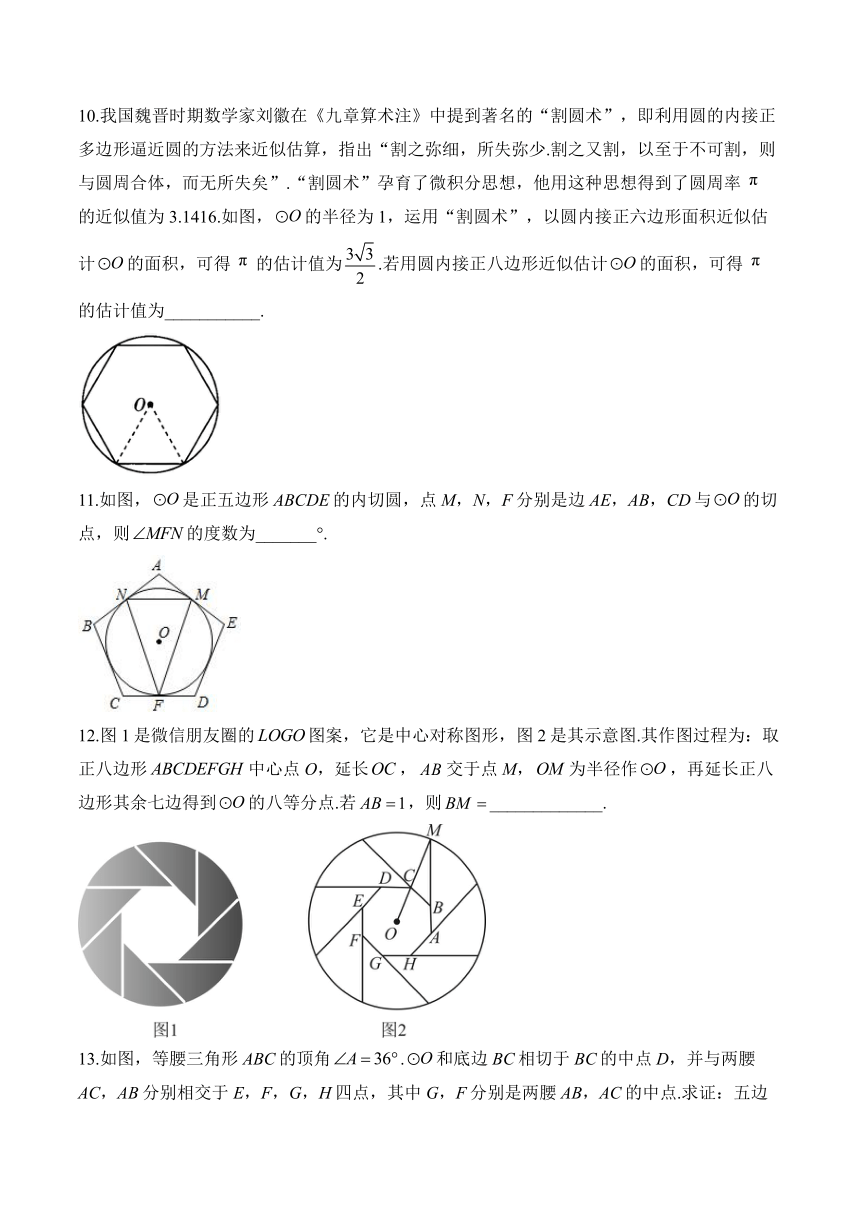
10.我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为.若用圆内接正八边形近似估计的面积,可得的估计值为___________.
11.如图,是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与的切点,则的度数为_______°.
12.图1是微信朋友圈的图案,它是中心对称图形,图2是其示意图.其作图过程为:取正八边形中心点O,延长,交于点M,为半径作,再延长正八边形其余七边得到的八等分点.若,则_____________.
13.如图,等腰三角形ABC的顶角.和底边BC相切于BC的中点D,并与两腰AC,AB分别相交于E,F,G,H四点,其中G,F分别是两腰AB,AC的中点.求证:五边形DEFGH是正五边形.
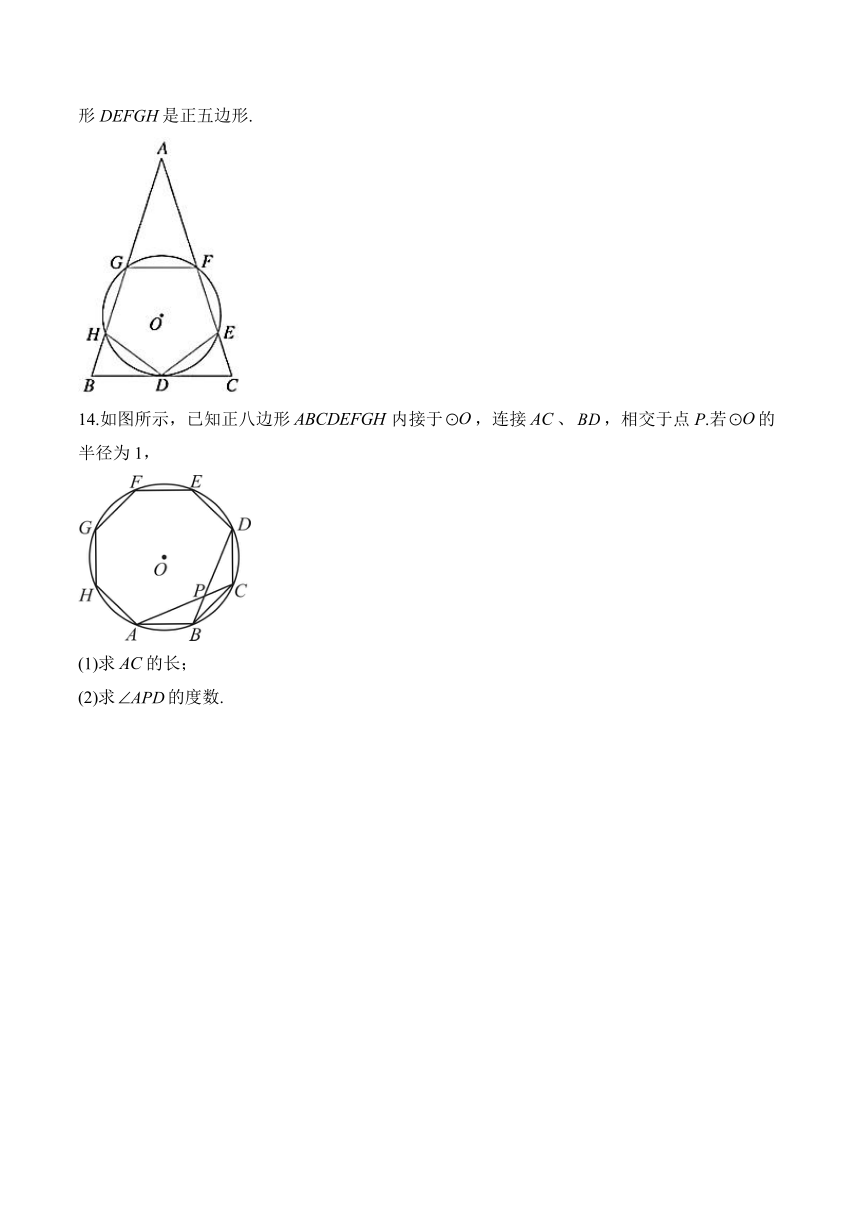
14.如图所示,已知正八边形内接于,连接、,相交于点P.若的半径为1,
(1)求的长;
(2)求的度数.
答案以及解析
1.答案:C
解析:如图,是等边三角形,边长为2,作于点D,
为等边的内切圆,
,
,
,
,
,
故选:C.
2.答案:C
解析:连接,,
∵多边形是正六边形,
∴,
∵,
∴是等边三角形,
∴,
∵正六边形的周长是12,
∴,
∴的半径是2
故选:C
3.答案:D
解析:连接与交于点O,
为正六边形,
,,
为等边三角形,
,
即正六边形的边长为,
故选:D.
4.答案:C
解析:如图所示,连接BE、CE,CF,则O为正六边形的中心,
∵正六边形的每个中心角都是60°,
∴每条边和中心构成的三角形都是等边三角形,
∴,
∵正六边形的每个内角都是120°,
∴中,,,
∴,
∴中,,则,
∵,∴,
∵,∴,
∴,
∵,∴,
∵,即,
∴.
故选:C.
5.答案:A
解析:如图,连接,,,
六边形是边长为4的正六边形,
是等边三角形,
,
,
边长为4的正六边形外接圆的半径为4,其内切圆的半径为.
故选:A.
6.答案:A
解析:A、任何三角形有且只有一个内切圆,则A正确;
B、不共线的三点确定一个圆,则B错误;
C、三角形内心到三边的距离相等,则C错误;
D、过半径的外端垂直于半径的直线是圆的切线,则D错误.
故选:A.
7.答案:B
解析:连接BO,CO,如图,
由题意可得,,,则,,.
8.答案:A
解析:连接OB,OD,OE,
E为的中点,
,,
正方形内接于,
,
,
根据勾股定理可得:,
即,
解得:,
即,
,
根据勾股定理可得:,
设,则,
根据勾股定理可得:,,
,
解得:,
即,
,
故选:A.
9.答案:
解析:的半径为3,
根据作图过程可得:,
这个多边形的周长为:,
即这个多边形的周长为.
故答案为:.
10.答案:
解析:如图,连接OA,OB,则,过点A作于点C,则,正八边形的面积为,,,即的估计值为.
11.答案:36
解析:如图,连接OM,ON.
M,N,F分别是AE,AB,CD与的切点,
,,
,
,
,
,
故答案为:36.
12.答案:/
解析:连接,,过C作于T,
在正八边形中,,,
,
,,
,,
,则,
,
,
,
在中,,,
等腰直角三角形,则,
由勾股定理得,
,则,
,
故答案为:.
13.答案:证明见解析
解析:证明:G,F分别是AB,AC的中点,,,
,且,,
.
.
如图所示,连接GD,OH,OD.
G,D分别是AB,BC的中点,.
,.
..
又,,.
.
同理,,.
.
.
G,H,D,E,F为的五等分点,
五边形DEFGH是正五边形.
14.答案:(1)
(2)
解析:(1)如图,连接,,与交于点Q,
由题意可知,,,
多边形是正八边形,
,
,
,
;
(2)所对的圆心角为,
所对的圆周角为,
,
.
1.一个等边三角形的边长为2,则这个等边三角形的内切圆半径为( )
A. B.1 C. D.
2.如图,正六边形内接于,正六边形的周长是12,则的半径是( )
A.1 B. C.2 D.
3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
4.如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若,则表示实数a的点落在数轴上(如图2)标有四段中的( )
A.段① B.段② C.段③ D.段④
5.若正六边形的边长为4,则其外接圆半径与内切圆半径的大小分别是( )
A.4, B.4,2 C.,2 D.,
6.在下列命题中,正确的是( )
A.任何三角形有且只有一个内切圆
B.三点确定一个圆
C.三角形的内心到三角形的三个顶点的距离相等
D.垂直于半径的直线一定是这个圆的切线
7.如图,是的内接正三角BC形,四边形ACEF是的内接正四边形.若线段BC恰是的一个内接正n边形的一条边,则( )
A.16 B.12 C.10 D.8
8.如图,正方形内接于,E为的中点,直线交于点F,如果的半径为,则点O到的距离( )
A. B. C.1 D.
9.如图,已知点A是半径为3的上任意一点,以点A为圆心,为半径做弧,交于点B,以点B为圆心,为半径做弧交于点C,同上述作图方法逆时针做出点D,E,F,依次连接,则这个多边形的周长为_________________.
10.我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为.若用圆内接正八边形近似估计的面积,可得的估计值为___________.
11.如图,是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与的切点,则的度数为_______°.
12.图1是微信朋友圈的图案,它是中心对称图形,图2是其示意图.其作图过程为:取正八边形中心点O,延长,交于点M,为半径作,再延长正八边形其余七边得到的八等分点.若,则_____________.
13.如图,等腰三角形ABC的顶角.和底边BC相切于BC的中点D,并与两腰AC,AB分别相交于E,F,G,H四点,其中G,F分别是两腰AB,AC的中点.求证:五边形DEFGH是正五边形.
14.如图所示,已知正八边形内接于,连接、,相交于点P.若的半径为1,
(1)求的长;
(2)求的度数.
答案以及解析
1.答案:C
解析:如图,是等边三角形,边长为2,作于点D,
为等边的内切圆,
,
,
,
,
,
故选:C.
2.答案:C
解析:连接,,
∵多边形是正六边形,
∴,
∵,
∴是等边三角形,
∴,
∵正六边形的周长是12,
∴,
∴的半径是2
故选:C
3.答案:D
解析:连接与交于点O,
为正六边形,
,,
为等边三角形,
,
即正六边形的边长为,
故选:D.
4.答案:C
解析:如图所示,连接BE、CE,CF,则O为正六边形的中心,
∵正六边形的每个中心角都是60°,
∴每条边和中心构成的三角形都是等边三角形,
∴,
∵正六边形的每个内角都是120°,
∴中,,,
∴,
∴中,,则,
∵,∴,
∵,∴,
∴,
∵,∴,
∵,即,
∴.
故选:C.
5.答案:A
解析:如图,连接,,,
六边形是边长为4的正六边形,
是等边三角形,
,
,
边长为4的正六边形外接圆的半径为4,其内切圆的半径为.
故选:A.
6.答案:A
解析:A、任何三角形有且只有一个内切圆,则A正确;
B、不共线的三点确定一个圆,则B错误;
C、三角形内心到三边的距离相等,则C错误;
D、过半径的外端垂直于半径的直线是圆的切线,则D错误.
故选:A.
7.答案:B
解析:连接BO,CO,如图,
由题意可得,,,则,,.
8.答案:A
解析:连接OB,OD,OE,
E为的中点,
,,
正方形内接于,
,
,
根据勾股定理可得:,
即,
解得:,
即,
,
根据勾股定理可得:,
设,则,
根据勾股定理可得:,,
,
解得:,
即,
,
故选:A.
9.答案:
解析:的半径为3,
根据作图过程可得:,
这个多边形的周长为:,
即这个多边形的周长为.
故答案为:.
10.答案:
解析:如图,连接OA,OB,则,过点A作于点C,则,正八边形的面积为,,,即的估计值为.
11.答案:36
解析:如图,连接OM,ON.
M,N,F分别是AE,AB,CD与的切点,
,,
,
,
,
,
故答案为:36.
12.答案:/
解析:连接,,过C作于T,
在正八边形中,,,
,
,,
,,
,则,
,
,
,
在中,,,
等腰直角三角形,则,
由勾股定理得,
,则,
,
故答案为:.
13.答案:证明见解析
解析:证明:G,F分别是AB,AC的中点,,,
,且,,
.
.
如图所示,连接GD,OH,OD.
G,D分别是AB,BC的中点,.
,.
..
又,,.
.
同理,,.
.
.
G,H,D,E,F为的五等分点,
五边形DEFGH是正五边形.
14.答案:(1)
(2)
解析:(1)如图,连接,,与交于点Q,
由题意可知,,,
多边形是正八边形,
,
,
,
;
(2)所对的圆心角为,
所对的圆周角为,
,
.
