28.2 用样本估计总体(含详解)九年级数学华东师大版(2012)下册课后培优检测
文档属性
| 名称 | 28.2 用样本估计总体(含详解)九年级数学华东师大版(2012)下册课后培优检测 | 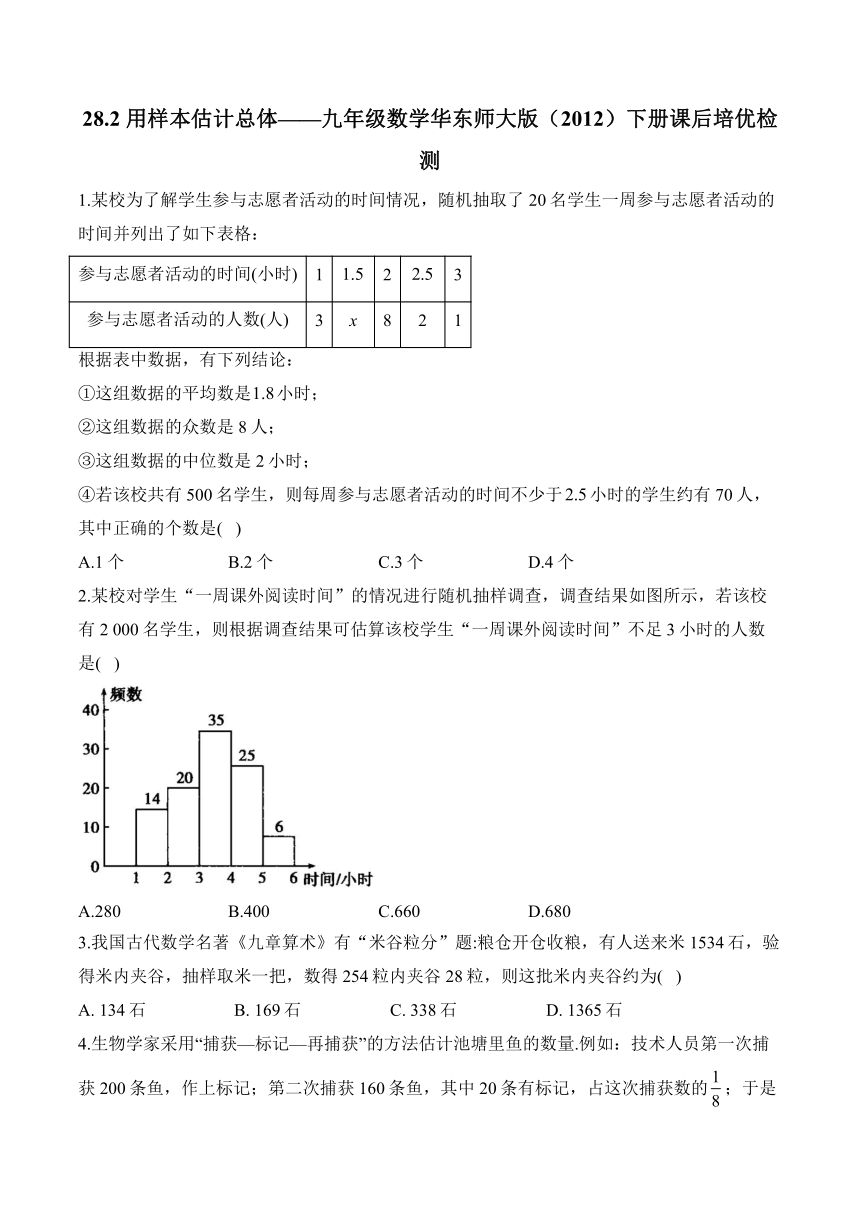 | |
| 格式 | docx | ||
| 文件大小 | 490.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 21:50:07 | ||
图片预览



文档简介
28.2 用样本估计总体——九年级数学华东师大版(2012)下册课后培优检测
1.某校为了解学生参与志愿者活动的时间情况,随机抽取了20名学生一周参与志愿者活动的时间并列出了如下表格:
参与志愿者活动的时间(小时) 1 2 3
参与志愿者活动的人数(人) 3 x 8 2 1
根据表中数据,有下列结论:
①这组数据的平均数是小时;
②这组数据的众数是8人;
③这组数据的中位数是2小时;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于小时的学生约有70人,
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
2.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如图所示,若该校有2 000名学生,则根据调查结果可估算该校学生“一周课外阅读时间”不足3小时的人数是( )
A.280 B.400 C.660 D.680
3.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A. 134石 B. 169石 C. 338石 D. 1365石
4.生物学家采用“捕获—标记—再捕获”的方法估计池塘里鱼的数量.例如:技术人员第一次捕获200条鱼,作上标记;第二次捕获160条鱼,其中20条有标记,占这次捕获数的;于是推断出第一次捕获的200条鱼大约也是总数的,所以池塘中大约有1600条鱼.这里用到的数学思想是( )
A.样本估计总体思想 B.公理化思想
C.分类讨论思想 D.数形结合思想
5.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林,一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A. 10 000只 B.5000只 C. 50 000只 D.1000只
6.在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 1 2 3 4 5 6 7 8 9 10
黑棋子枚数 1 3 0 2 3 4 2 1 1 3
根据以上数据,估算袋中的白棋子数量为( )
A.60枚 B.50枚 C.40枚 D.30枚
7.为调查某校1 500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )
A.1 200名 B.450名 C.400名 D.300名
8.近几年来,人们的支付方式发生了巨大转变,移动支付已成为主要的支付方式之一.某校为了解本校学生某月A B两种移动支付方式的使用情况,从全校1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A种支付方式和仅使用B种支付方式的学生的支付金额a(元)的分布情况如下:
支付金额a/元 a>2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生仅使用A种支付方式的概率大于他仅使用B种支付方式的概率;
②根据样本数据估计,全校1000名学生中,同时使用A, B两种支付方式的有400人;
③样本中仅使用A种支付方式的学生,该月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的学生,该月的支付金额的平均数一定不低于1000元.
其中所有合理的推断的序号是( )
A.①③ B.②④ C.①②③ D.①②③④
9.小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区60户家庭某一天各类生活垃圾的投放量,统计得出这60户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示).根据以上信息,估计该小区300户居民这一天投放的可回收物共约__________千克.
10.为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出100条鱼苗,每条做好记号,然后放回原鱼池.一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出100条鱼苗,发现其中有记号的鱼苗分别是5条、10条,可以初步估计鱼苗数目较多的是__________鱼池.(填“甲”或“乙”)
11.光明中学环保小组对某8个餐厅一天的快餐饭盒使用个数作了调查,结果如下:
125,115,140,270,110,120,100,140.
(1)这8个餐厅平均每个餐厅一天用__________个饭盒.
(2)如果该区共有这种类似的餐厅62个,且所调查的8个餐厅是从这62个餐厅中随机抽取的,试问该地区一天共使用的快餐饭盒大约有__________个.
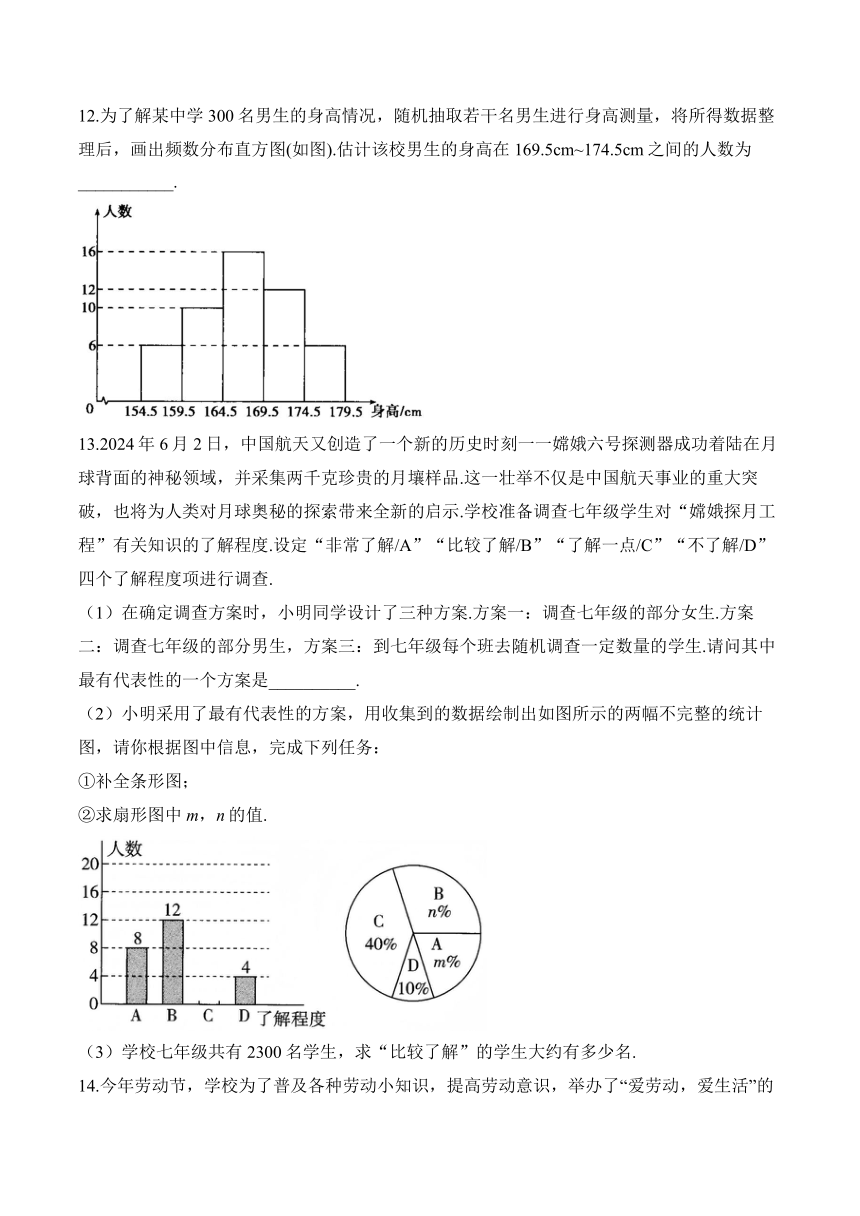
12.为了解某中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).估计该校男生的身高在169.5cm~174.5cm之间的人数为___________.
13.2024年6月2日,中国航天又创造了一个新的历史时刻一一嫦娥六号探测器成功着陆在月球背面的神秘领域,并采集两千克珍贵的月壤样品.这一壮举不仅是中国航天事业的重大突破,也将为人类对月球奥秘的探索带来全新的启示.学校准备调查七年级学生对“嫦娥探月工程”有关知识的了解程度.设定“非常了解/A”“比较了解/B”“了解一点/C”“不了解/D”四个了解程度项进行调查.
(1)在确定调查方案时,小明同学设计了三种方案.方案一:调查七年级的部分女生.方案二:调查七年级的部分男生,方案三:到七年级每个班去随机调查一定数量的学生.请问其中最有代表性的一个方案是__________.
(2)小明采用了最有代表性的方案,用收集到的数据绘制出如图所示的两幅不完整的统计图,请你根据图中信息,完成下列任务:
①补全条形图;
②求扇形图中m,n的值.
(3)学校七年级共有2300名学生,求“比较了解”的学生大约有多少名.
14.今年劳动节,学校为了普及各种劳动小知识,提高劳动意识,举办了“爱劳动,爱生活”的知识竞赛.某校初一年级有400人、初二年级有800人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一: 68 88 100 100 79 94 89 85 100 88
100 90 98 97 77 94 96 100 92 67
初二: 69 97 96 89 98 100 99 100 95 100
99 69 97 100 99 94 79 99 98 79
根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
初一人数 2 2 4 12
初二人数 2 2 15
分析数据:样本数据的平均数、中位数、满分率如表:
年级 平均数 中位数 满分率
初一 90.1 93
初二 92.8
得出结论:
(1)________;________;________;
(2)你认为哪个年级掌握劳动知识的总体水平较好,说明理由;
(3)请你估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共多少人.
答案以及解析
1.答案:B
解析:由题意得,;
①这组数据的平均数是(小时),故①正确;
②由于活动时间为2小时的人数最多,则这组数据的众数是2小时,故②错误;
③把这20人的活动时间从低到高排列,处在第10名和第11名的时间分别为2小时,2小时,则这组数据的中位数是(小时),故③正确;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于小时的学生约有(人),故④错误;
∴正确的有2个,
故选:B.
2.答案:D
解析:
∴估算该校学生“一周课外阅读时间”不足3小时的人数为680.故选D.
3.答案:B
解析:根据题意,得石,故这批米内夹谷约169石.
4.答案:A
解析:根据条件可知,生物学家用第一次捕获和第二次捕获的标记数目进行计算总数,所用数学思想为“样本估计总体思想” .
故选:A.
5.答案:A
解析:(只),故选A.
6.答案:C
解析:根据试验提供的数据,黑棋子的比例为所以白棋子的比例为所以袋中的白棋子数量约为(枚).故选C.
7.答案:D
解析:本题考查用样本估计总体.∵该校喜爱体育节目的学生占,该校共1 500名学生,∴该校喜爱体育节目的学生共有(名),故选D.
8.答案:C
解析:样本中仅使用A种支付方式的学生人数为,仅使用B种支付方式的学生人数为,A,B两种支付方式都不使用的学生人数为5,则同时使用A,B两种支付方式的学生人数为,故估计全校1000名学生中,同时使用A,B两种支付方式的有(人),故②正确.若从样本中随机抽取一名学生,则该生仅使用A种支付方式的概率,仅使用B种支付方式的概率为,故该生仅使用A种支付方式的概率大于他仅使用B种支付方式的概率,故①正确.将样本中仅使用A种支付方式的学生的支付金额按大小顺序排列,第15,16个数据均在范围内,故中位数一定不超过1000元,故③正确.无法估计样本中仅使用B种支付方式的学生的支付金额的平均数是否低于1000元,故④错误.
9.答案:75
解析:估计该小区300户居民这一天投放的可回收物共约(千克),故答案为75.
10.答案:甲
解析:由题意可得,甲鱼池中的鱼苗数目约为,乙鱼池中的鱼苗数目约为.,初步估计鱼苗数目较多的是甲鱼池,故答案为甲.
11.答案:(1)140
(2)8680
解析:(1)(个).
(2)(个).
12.答案:72
解析:根据题图知,身高在169.5cm~174.5cm之间的人数12所占的百分比为,则估计该校男生的身高在169.5cm~174.5cm之间的有300×24%=72(人).
13.答案:(1)方案三
(2)①图见解析
②,
(3)690名
解析:(1)方案三
(2)①由题意知,共调查了学生(名),
所以了解程度为C的学生有(名).
补全条形图如图所示.
②样本中了解程度为A的学生所占的百分比为,.
样本中了解程度为B的学生所占的百分比为,.
(3)(名).
答:学校七年级2300名学生中“比较了解”的学生大约有690名.
14.答案:(1)1,97.5,25
(2)初二年级掌握劳动知识的总体水平较好,理由见解析
(3)估计该校两个年级在本次测试中可以得到满分的人数共260人
解析:;
将初二的学生成绩从小到大排列:69,69,79,79,89,94,95,96,97,97,98,98,99,99,99,99,100,100,100,100,
∴,
初一成绩满分的学生人数为5人,
∴,
∴;
故答案为:1,97.5,25;
(1)解:初二年级掌握劳动知识的总体水平较好,理由如下:
初二年级成绩的平均数高于初一年级,求中位数高一初一年级,说明高分段的学生数量高于初一年级,所以初二年级掌握劳动知识的总体水平较好.
(3)解:人;
答:估计该校两个年级在本次测试中可以得到满分的人数共260人.
1.某校为了解学生参与志愿者活动的时间情况,随机抽取了20名学生一周参与志愿者活动的时间并列出了如下表格:
参与志愿者活动的时间(小时) 1 2 3
参与志愿者活动的人数(人) 3 x 8 2 1
根据表中数据,有下列结论:
①这组数据的平均数是小时;
②这组数据的众数是8人;
③这组数据的中位数是2小时;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于小时的学生约有70人,
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
2.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如图所示,若该校有2 000名学生,则根据调查结果可估算该校学生“一周课外阅读时间”不足3小时的人数是( )
A.280 B.400 C.660 D.680
3.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A. 134石 B. 169石 C. 338石 D. 1365石
4.生物学家采用“捕获—标记—再捕获”的方法估计池塘里鱼的数量.例如:技术人员第一次捕获200条鱼,作上标记;第二次捕获160条鱼,其中20条有标记,占这次捕获数的;于是推断出第一次捕获的200条鱼大约也是总数的,所以池塘中大约有1600条鱼.这里用到的数学思想是( )
A.样本估计总体思想 B.公理化思想
C.分类讨论思想 D.数形结合思想
5.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林,一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A. 10 000只 B.5000只 C. 50 000只 D.1000只
6.在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 1 2 3 4 5 6 7 8 9 10
黑棋子枚数 1 3 0 2 3 4 2 1 1 3
根据以上数据,估算袋中的白棋子数量为( )
A.60枚 B.50枚 C.40枚 D.30枚
7.为调查某校1 500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )
A.1 200名 B.450名 C.400名 D.300名
8.近几年来,人们的支付方式发生了巨大转变,移动支付已成为主要的支付方式之一.某校为了解本校学生某月A B两种移动支付方式的使用情况,从全校1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A种支付方式和仅使用B种支付方式的学生的支付金额a(元)的分布情况如下:
支付金额a/元 a>2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生仅使用A种支付方式的概率大于他仅使用B种支付方式的概率;
②根据样本数据估计,全校1000名学生中,同时使用A, B两种支付方式的有400人;
③样本中仅使用A种支付方式的学生,该月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的学生,该月的支付金额的平均数一定不低于1000元.
其中所有合理的推断的序号是( )
A.①③ B.②④ C.①②③ D.①②③④
9.小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区60户家庭某一天各类生活垃圾的投放量,统计得出这60户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示).根据以上信息,估计该小区300户居民这一天投放的可回收物共约__________千克.
10.为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出100条鱼苗,每条做好记号,然后放回原鱼池.一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出100条鱼苗,发现其中有记号的鱼苗分别是5条、10条,可以初步估计鱼苗数目较多的是__________鱼池.(填“甲”或“乙”)
11.光明中学环保小组对某8个餐厅一天的快餐饭盒使用个数作了调查,结果如下:
125,115,140,270,110,120,100,140.
(1)这8个餐厅平均每个餐厅一天用__________个饭盒.
(2)如果该区共有这种类似的餐厅62个,且所调查的8个餐厅是从这62个餐厅中随机抽取的,试问该地区一天共使用的快餐饭盒大约有__________个.
12.为了解某中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).估计该校男生的身高在169.5cm~174.5cm之间的人数为___________.
13.2024年6月2日,中国航天又创造了一个新的历史时刻一一嫦娥六号探测器成功着陆在月球背面的神秘领域,并采集两千克珍贵的月壤样品.这一壮举不仅是中国航天事业的重大突破,也将为人类对月球奥秘的探索带来全新的启示.学校准备调查七年级学生对“嫦娥探月工程”有关知识的了解程度.设定“非常了解/A”“比较了解/B”“了解一点/C”“不了解/D”四个了解程度项进行调查.
(1)在确定调查方案时,小明同学设计了三种方案.方案一:调查七年级的部分女生.方案二:调查七年级的部分男生,方案三:到七年级每个班去随机调查一定数量的学生.请问其中最有代表性的一个方案是__________.
(2)小明采用了最有代表性的方案,用收集到的数据绘制出如图所示的两幅不完整的统计图,请你根据图中信息,完成下列任务:
①补全条形图;
②求扇形图中m,n的值.
(3)学校七年级共有2300名学生,求“比较了解”的学生大约有多少名.
14.今年劳动节,学校为了普及各种劳动小知识,提高劳动意识,举办了“爱劳动,爱生活”的知识竞赛.某校初一年级有400人、初二年级有800人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一: 68 88 100 100 79 94 89 85 100 88
100 90 98 97 77 94 96 100 92 67
初二: 69 97 96 89 98 100 99 100 95 100
99 69 97 100 99 94 79 99 98 79
根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段
初一人数 2 2 4 12
初二人数 2 2 15
分析数据:样本数据的平均数、中位数、满分率如表:
年级 平均数 中位数 满分率
初一 90.1 93
初二 92.8
得出结论:
(1)________;________;________;
(2)你认为哪个年级掌握劳动知识的总体水平较好,说明理由;
(3)请你估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共多少人.
答案以及解析
1.答案:B
解析:由题意得,;
①这组数据的平均数是(小时),故①正确;
②由于活动时间为2小时的人数最多,则这组数据的众数是2小时,故②错误;
③把这20人的活动时间从低到高排列,处在第10名和第11名的时间分别为2小时,2小时,则这组数据的中位数是(小时),故③正确;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于小时的学生约有(人),故④错误;
∴正确的有2个,
故选:B.
2.答案:D
解析:
∴估算该校学生“一周课外阅读时间”不足3小时的人数为680.故选D.
3.答案:B
解析:根据题意,得石,故这批米内夹谷约169石.
4.答案:A
解析:根据条件可知,生物学家用第一次捕获和第二次捕获的标记数目进行计算总数,所用数学思想为“样本估计总体思想” .
故选:A.
5.答案:A
解析:(只),故选A.
6.答案:C
解析:根据试验提供的数据,黑棋子的比例为所以白棋子的比例为所以袋中的白棋子数量约为(枚).故选C.
7.答案:D
解析:本题考查用样本估计总体.∵该校喜爱体育节目的学生占,该校共1 500名学生,∴该校喜爱体育节目的学生共有(名),故选D.
8.答案:C
解析:样本中仅使用A种支付方式的学生人数为,仅使用B种支付方式的学生人数为,A,B两种支付方式都不使用的学生人数为5,则同时使用A,B两种支付方式的学生人数为,故估计全校1000名学生中,同时使用A,B两种支付方式的有(人),故②正确.若从样本中随机抽取一名学生,则该生仅使用A种支付方式的概率,仅使用B种支付方式的概率为,故该生仅使用A种支付方式的概率大于他仅使用B种支付方式的概率,故①正确.将样本中仅使用A种支付方式的学生的支付金额按大小顺序排列,第15,16个数据均在范围内,故中位数一定不超过1000元,故③正确.无法估计样本中仅使用B种支付方式的学生的支付金额的平均数是否低于1000元,故④错误.
9.答案:75
解析:估计该小区300户居民这一天投放的可回收物共约(千克),故答案为75.
10.答案:甲
解析:由题意可得,甲鱼池中的鱼苗数目约为,乙鱼池中的鱼苗数目约为.,初步估计鱼苗数目较多的是甲鱼池,故答案为甲.
11.答案:(1)140
(2)8680
解析:(1)(个).
(2)(个).
12.答案:72
解析:根据题图知,身高在169.5cm~174.5cm之间的人数12所占的百分比为,则估计该校男生的身高在169.5cm~174.5cm之间的有300×24%=72(人).
13.答案:(1)方案三
(2)①图见解析
②,
(3)690名
解析:(1)方案三
(2)①由题意知,共调查了学生(名),
所以了解程度为C的学生有(名).
补全条形图如图所示.
②样本中了解程度为A的学生所占的百分比为,.
样本中了解程度为B的学生所占的百分比为,.
(3)(名).
答:学校七年级2300名学生中“比较了解”的学生大约有690名.
14.答案:(1)1,97.5,25
(2)初二年级掌握劳动知识的总体水平较好,理由见解析
(3)估计该校两个年级在本次测试中可以得到满分的人数共260人
解析:;
将初二的学生成绩从小到大排列:69,69,79,79,89,94,95,96,97,97,98,98,99,99,99,99,100,100,100,100,
∴,
初一成绩满分的学生人数为5人,
∴,
∴;
故答案为:1,97.5,25;
(1)解:初二年级掌握劳动知识的总体水平较好,理由如下:
初二年级成绩的平均数高于初一年级,求中位数高一初一年级,说明高分段的学生数量高于初一年级,所以初二年级掌握劳动知识的总体水平较好.
(3)解:人;
答:估计该校两个年级在本次测试中可以得到满分的人数共260人.
