【小升初押题卷】小升初重点中学择校分班预测卷(含解析)2024-2025学年六年级下学期数学青岛版(六三制)
文档属性
| 名称 | 【小升初押题卷】小升初重点中学择校分班预测卷(含解析)2024-2025学年六年级下学期数学青岛版(六三制) |

|
|
| 格式 | docx | ||
| 文件大小 | 248.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 08:02:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初重点中学择校分班预测卷
一、选择题
1.10克糖溶解在100克水中,糖和糖水重量的比是( )。
A.11∶1 B.1∶11 C.1∶10 D.1∶12
2.下面直线上点P表示的数是( )。
A.﹣2.5 B.﹣1.5 C.﹣0.5 D.1.5
3.如图中,正方形的边长都是10cm。请你比较一下,如图各图阴影部分面积和左边第一个阴影部分面积相等的有( )个。
A.1个 B.2个 C.3个 D.4个
4.九月份用水比八月份节约了9%,也就是九月份用水是八月份的( )。
A.109% B.91% C.9% D.无法判断
5.A÷3=B×7,A和B的最简整数比是( )。
A.3∶7 B.21∶1 C.7∶3
6.把一个圆柱的侧面展开,不可能是( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
7.一张边长为4分米的正方形纸,如果在这张纸上剪4个相等并且最大的圆,4个圆的面积和是这张纸的( ).
A.78.5% B.80% C.75%
二、填空题
8.0.55∶的比值是( ),( )公顷比15公顷多20%。
9. ÷12= ∶ == %。
10.甘肃省海拔最低处是陇南白龙江中游文县罐子沟,海拔是550米,记作﹢550米,中国海拔最低处是新疆艾丁湖,低于海平面154.21米,记作( )米。
11.甲数是乙数的60%,甲数比乙数少 % ,乙数比甲数多 % .
12.在比例式7:2=21:6中,如果第一个比的后项加上6,那么第二个比的后项要加上 等式才成立.
13.等底等高的圆柱和圆锥的体积相差16立方分米,这个圆柱的体积是( )。
14.( )÷20==( )∶4=( )%=1.25。
15.用小棒摆五边形,如下图所示。
按照这样的方法继续摆下去,摆第5幅图需要( )根小棒,摆第n幅图需要( )根小棒。
三、判断题
16.把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的。( )
17.圆柱的体积是圆锥体积的。( )
18.,,,,……这列数越来越接近0. ( )
19.小麦每公顷产量一定,小麦的总产量与公顷数成反比例。( )
20.4,,0.5,这四个数能组成比例. ( )
21.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒。( )
四、计算题
22.直接写得数。
60×20= 0÷36= 7.2+2.87= 908-303≈
25×4%= 5÷×4 =
23.计算下面各题,能简算的要简算.
×15.31+×2.69 24×+76÷5 14.25-2.83-0.17
375+450÷18×25 [×(-)]÷
24.解方程或比例。
x÷6=48% x-8=20 ∶x=∶9
25.求总支出是多少元?
五、作图题
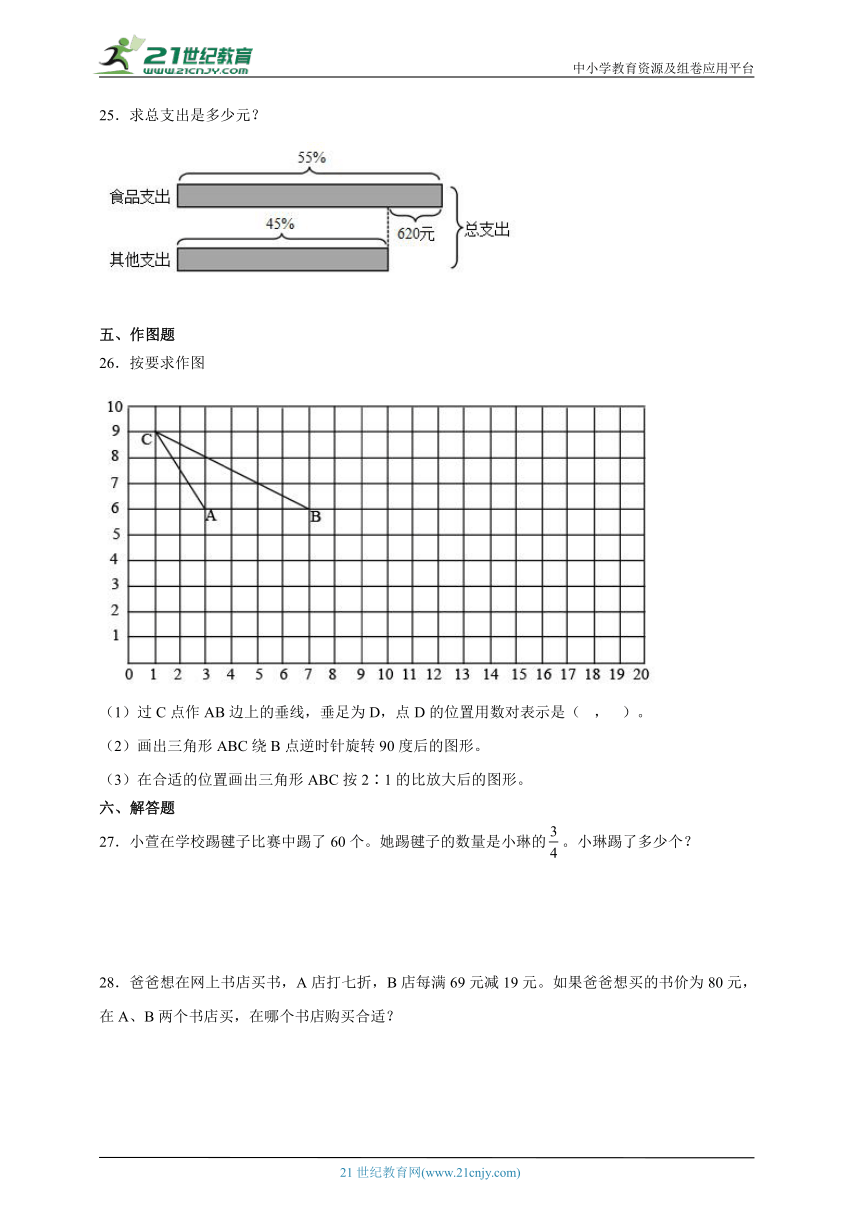
26.按要求作图
(1)过C点作AB边上的垂线,垂足为D,点D的位置用数对表示是( , )。
(2)画出三角形ABC绕B点逆时针旋转90度后的图形。
(3)在合适的位置画出三角形ABC按2∶1的比放大后的图形。
六、解答题
27.小萱在学校踢毽子比赛中踢了60个。她踢毽子的数量是小琳的。小琳踢了多少个?
28.爸爸想在网上书店买书,A店打七折,B店每满69元减19元。如果爸爸想买的书价为80元,在A、B两个书店买,在哪个书店购买合适?
29.将一个底面周长是18.84厘米、高是10厘米的圆柱形量杯里装满水,再倒入一个长12厘米、宽5厘米的长方体容器中,水面高是多少厘米?
30.王芳买了一听圆柱形易拉罐包装的饮料,侧面有“净含量320毫升”的字样,从饮料罐外面量,底面直径6厘米,高1.2分米。请问这家生产商是否欺骗消费者?
31.修一条公路,修了全长的后,离这条公路的中点还有1.7千米。这条公路全长多少千米?
32.如图所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加80平方厘米。
(1)同学们回忆圆柱体积计算公式的推导过程,用自己喜欢的方式将它记录下来。
(2)那么圆柱的高是多少厘米?长方体的体积是多少立方厘米?
33.六年级三个班级同学植树,六(1)班植树棵数占总棵数的40%,六(2)班、六(3)班植树棵数的比是2∶3,六(1)班比六(2)班多植树32棵。三个班种树多少棵?
答案与解析
1.B
【精讲精析】已知10克糖溶解在100克水中,则糖水的重量是(10+100)克;根据比的意义写出糖和糖水的重量比,并化简比。
【解题思路】10∶(10+100)
=10∶110
=(10÷10)∶(110÷10)
=1∶11
糖和糖水重量的比是1∶11。
故答案为:B
2.C
【精讲精析】直线上点P表示的数是0和﹣1的中点,即﹣0.5,也可以用(1+0)÷2来计算,再加上负号即可。
【解题思路】下面直线上点P表示的数是﹣0.5。
故答案为:C
【要点提升】此题主要考查负数的意义和数轴的认识。
3.D
【精讲精析】正方形面积公式S正=a2(a为边长),圆的面积公式S圆=πr2,据此分别计算出每个图形的面积再比较。
【解题思路】计算第一个图形阴影部分面积:
第一个图形中,正方形边长为10cm,圆的直径等于正方形边长10cm,半径r=10÷2=5cm。根据正方形面积S正=10×10=100cm2;圆的面积S圆=π×52= 25πcm2,那么阴影部分面积S1=100-25πcm2。
计算第二个图形阴影部分面积:
第二个图形中,扇形半径等于正方形边长10cm ,扇形面积S扇=πr2=π×102=25πcm2,正方形面积是100cm2,阴影部分面积S2=100-25πcm2,与第一个图形阴影部分面积相等。
计算第三个图形阴影面积:
第三个图形中,4个小圆的直径为10÷2=5cm,半径r=5÷2=2.5cm。4个小圆的面积和S4圆=4×π×2.52=4×π×=25πcm2正方形面积是100cm2,阴影部分面积S3=100-25πcm2,与第一个图形阴影部分面积相同。
计算第四个图形阴影面积:
第四个图形中,把图形中空白部分拼合起来,可得到一个半径为5cm的圆,其面积为25πcm2,正方形面积是100cm2 ,阴影部分面积S4=100-25πcm2 ,与第一个图形阴影部分面积相等。
计算第五个图形阴影面积。
第五个图形中,两个半圆可以拼成一个直径为10cm,半径为5cm的圆,圆的面积是25πcm2 ,正方形面积是100cm2 ,阴影部分面积S5=100-25πcm2,与第一个图形阴影部分面积相等。
综上分析所述,如图各图阴影部分面积和左边第一个阴影部分面积相等的有4个。
故答案为:D
4.B
【精讲精析】分析题目,把八月份的用水量看作单位“1”,则九月份的用水量是(1-9%),根据求一个数是另一个数的百分之几是多少用除法用九月份的用水量除以八月份的用水量即可解答。
【解题思路】假设八月份的用水量是1,则九月份的用水量是1-9%=91%。
91%÷1=91%
九月份用水比八月份节约了9%,也就是九月份用水是八月份的91%。
故答案为:B
5.B
【精讲精析】假设结果是1,根据除法和乘法各部分之间的关系,分别求出A和B,写出A和B的比,化简即可。
【解题思路】(1×3)∶(1÷7)
=3∶
=21∶1
故答案为:B
【要点提升】两数相除又叫两个数的比,化简比根据比的基本性质。
6.D
【精讲精析】圆柱的展开图可能是正方形、可能是长方形、也可能是平行四边形,根据圆柱的侧面展开图的特点,结合圆柱的侧面的几种展开图方法与展开图的特点即可进行选择。
【解题思路】圆柱的侧面沿高展开可能是长方形或正方形,如果斜着展开是一个平行四边形,因为圆柱的上下底面是完全相同的两个圆,所以圆柱的侧面展开图不可能是梯形。
故答案为:D
7.A
8. 1.1 18
【精讲精析】求比值,用前项除以后项即可;
把15公顷看成单位“1”,要求的面积比15公顷多20%,先用15公顷乘20%,求出多的部分,再加上15公顷即可。
【解题思路】0.55÷=1.1
15×20%+15
=3+15
=18(公顷)
【要点提升】本题考查了求比值以及求比一个数多百分之几的数是多少,只要找清单位“1”,利用基本数量关系解决问题。
9. 9 3 4 75
【精讲精析】根据分数与比、分数与除法的关系:=3∶4=3÷4,根据商不变的性质,被除数和除数同时乘3,分子除以分母。完成填空即可。
【解题思路】9÷12=3∶4==75%
【要点提升】解答此题的关键,根据小数、百分数、除法、比之间的关系及商不变的性质、比的基本性质即可进行转化。
10.﹣154.21
【精讲精析】通常把海平面的高度记作0,高出海平面记作“﹢”,低于海平面记作“﹣”。
【解题思路】由分析可知:
低于海平面154.21米,记作﹣154.21米。
【要点提升】本题是考查正、负数的意义及其应用。
11. 40 66.7
【精讲精析】把乙数看作单位“1”,则甲数为60%,则甲数比乙数少(1﹣60%);求乙数比甲数多几分之几,把甲数看作单位“1”,根据“(大数﹣小数)÷单位“1”的量”进行解答.
【解题思路】1﹣60%=40%;
(1﹣60%)÷60%,
=40%÷60%,
≈66.7%
故答案为40,66.7.
12.18
【解题思路】试题分析:第一个比的后项加6后变成7:8,要想使等式成立,就要让第二个比的最简比也应变成7:8,根据比的基本性质,7:8=(7×3):(8×3)=21:24,即第二个比的后项6加上18变成24,21:(6+18)=21:24=7:8,所以第二个比的后项应该加18才能使比例成立.
解答:解:7:(2+6)=7:8,
又7:8=(7×3):(8×3)=21:24
即需第二个比的后项6加上24﹣6=18,
所以第二个比的后项应该加18才能使比例成立;
故答案为18.
点评:完成本题要注意比值和原来不一样了,变化不是倍数关系.
13.24立方分米/24dm3
【精讲精析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,可以把圆锥的体积看作1份,则圆柱的体积是3份,相差(3-1)份;用等底等高的圆柱和圆锥的体积之差除以份数差,求出一份数,即是圆锥的体积,再乘3,就是这个圆柱的体积。
【解题思路】圆锥的体积:
16÷(3-1)
=16÷2
=8(立方分米)
圆柱的体积:
8×3=24(立方分米)
【要点提升】明确等底等高的圆柱与圆锥的体积关系,利用差倍问题的解题方法解答。
14.25;16;5;125
【精讲精析】根据比和百分数、分数、小数的关系,以及比和分数、除法的关系,分析填空即可。
【解题思路】因为4×1.25=5,5∶4==25÷20,1.25=125%,
所以25÷20==5∶4=125%=1.25。
【要点提升】本题考查了比和百分数、分数、小数的互化,属于综合性基础题,计算时需细心。
15. 21 4n+1
【精讲精析】第1幅图需要的小棒数为5根,即:4×1+1;第2幅图需要的小棒数为9根,即::4×2+1;第3幅图需要的小棒数为13根,即:4×3+1;……第n幅图需要的小棒数为: 4n+1;据此填空即可。
【解题思路】根据分析可得:
4×5+1
=20+1
=21(个)
所以,按照这样的方法继续摆下去,摆第5幅图需要21根小棒,摆第n幅图需要(4n+1)根小棒。
【要点提升】本题主要考查数与形结合的规律,发现每多1个幅图就多4根小棒是解本题的关键。
16.×
【精讲精析】根据题意,把一个圆柱削成一个圆锥,如果削成的圆锥与圆柱等底等高,那么圆锥的体积是圆柱体积的;如果削成的圆锥与圆柱不是等底等高,那么圆锥的体积就不是圆柱体积的;据此判断。
【解题思路】把一个圆柱削成一个与它等底等高的圆锥,这个圆锥的体积才是圆柱体积的。
原题说法错误。
故答案为:×
【要点提升】明确等底等高的圆柱和圆锥体积之间的关系是解题的关键。
17.×
18.√
【解题思路】,,,,……这个数列第一个数是,后面的数依次是前面一个数除以2的结果,因此分子1不变,分母从3开始以2倍的速度扩大,所以这列数越来越接近0.该说法正确.
19.×
【精讲精析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解题思路】小麦的总产量÷公顷数=小麦每公顷产量(一定),商一定,所以小麦每公顷产量成正比例。
故答案为:×
【要点提升】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
20.√
【解题思路】略
21.√
【精讲精析】规律:小棒的根数=小正方形的个数×3+1,根据这样的规律计算后做出判断即可。
【解题思路】摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
………
所以摆n个正方形要小棒:4+3×(n-1)=3n+1(根);
n=10,3×10+1=31(根);摆10个正方形一共需要31根小棒,原题说法正确。
故答案为:√
22.1200;0;10.07;600
1;;1;100
23.15; 20; 11.25;
1000;
24.x=2.88;x=35;x=24
【精讲精析】“x÷6=48%”将等式两边同时乘6,解出x;
“x-8=20”将等式两边同时加上8,再同时除以,解出x;
“∶x=∶9”先将比例写成一般方程,再将等式两边同时除以,解出x。
【解题思路】x÷6=48%
解:x=48%×6
x=2.88
x-8=20
解:x=20+8
x=28÷
x=35
∶x=∶9
解:x=9×
x=6÷
x=24
25.6200元
【精讲精析】根据图意可知,把总支出看作单位“1”,根据百分数除法的意义,用食品支出比其它支出多的钱数(620元)除以多占总支出的百分率(55%-45%)就是总支出。
【解题思路】620÷(55%-45%)
=620÷10%
=6200(元)
答:总支出是6200元。
【要点提升】此题是考查百分数除法的意义及应用。已知一个数的百分之几是多少,求这个数,用已知数除以它所对应的分率。
26.(1)画图见详解;(1,6)
(2)和(3)见详解
【精讲精析】(1)延长BA,再过C点向延长线上做垂线即可;数对中第一个数字表示列,第二个数字表示行,由此写出点D的位置即可;
(2)根据旋转的方法,将三角形与点B相连的两条边绕点B逆时针旋转90度,再将其它边连起来即可;
(3)将三角形ABC按2∶1的比放大,则放大后三角形的边长是原三角形的2倍,据此画图即可。
【解题思路】
点D的位置用数对表示是(1,6)。
【要点提升】本题综合性较强,熟练掌握数对表示位置的特点,图形旋转的方法以及图形放大与缩小的方法是解答本题的关键。
27.80个
【精讲精析】把小琳踢毽子的数量看作单位“1”,小萱踢毽子的数量是小琳的,对应的是小萱踢毽子的数量60个,求单位“1”,用60÷解答。
【解题思路】60÷
=60×
=80(个)
答:小琳踢了80个。
28.A店
【精讲精析】把在两家书店购买的价格算出来再比较,便宜的更合适:
A店:七折就是70%,把原价看作单位“1”,根据求一个数的百分之几是多少,用乘法计算。
B店:先用80除以69所得的商再乘19可得可减几元,最后用80减几即可得购买的价格。
【解题思路】A店:80×70%=56(元)
B店:
80-19×1
=80-19
=61(元)
56<61
答:到A店买更合适。
29.4.71厘米
【精讲精析】先求圆柱形容积,因为这部分水全部倒入了长方体容器中,所以用这部分体积去除长方体的底面积,可得到水面高度。
【解题思路】
=32×3.14×10÷60
=282.6÷60
=4.71(厘米)
答:水面高度是4.71厘米。
【要点提升】本题属于体积的等积变形,利用水的形状改变前后体积是不变的,确定改变后的体积,再计算出改变后的水的高度。
30.没有欺骗
【精讲精析】根据圆柱的体积公式:底面积×高,求出这个圆柱形易拉罐的体积,再和包装上的“净含量320毫升”比较,即可解答。
【解题思路】1.2分米=12厘米 320毫升=320立方厘米
圆柱体体积为3.14×(6÷2)2×12
=3.14×9×12
=339.12(立方厘米)
339.12立方厘米=339.12毫升
339.12>320
没有欺骗消费者。
答:这家生产商家没有欺骗消费者。
【要点提升】本题考查圆柱体的面积公式的应用;关键是熟记公式。
31.23.8千米
【精讲精析】把这条公路长度看作单位“1”,这条公路的中点就是公路长度的处,修了全长的后,再修全长的(-),也就是1.7千米占总长度的对应分率,根据部分数量÷对应分率=整体数量,列式解答即可。
【解题思路】1.7÷(-)
=1.7÷
=1.7×14
=23.8(千米)
答:这条公路全长23.8千米。
32.(1)把圆柱底面平均分成若干等份的小扇形,沿圆柱的高切开,拼成一近似的长方体。发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,长方体的体积等于底面积乘高,所以圆柱的体积也等于底面积乘高。若体积用字母V表示,底面积用字母S表示,高用h表示,即体积为:V=Sh;
(2)10厘米;502.4立方厘米
【精讲精析】(1)根据圆柱体积计算公式的推导过程解答即可;
(2)圆柱切成若干等分,拼成一个近似的长方体后,表面积比原来的圆柱的表面积增加了两个以圆柱的高和半径为边长的长方形的面积,体积与原来圆柱的体积相等;据此解答。
【解题思路】(1)把圆柱底面平均分成若干等份的小扇形,沿圆柱的高切开,拼成一近似的长方体。发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,长方体的体积等于底面积乘高,所以圆柱的体积也等于底面积乘高。若体积用字母∨表示,底面积用字母S表示,高用h表示,即体积为:V=Sh。
(2)80÷2÷(8÷2)
=40÷4
=10
3.14×(8÷2)2×10
=3.14×160
=502.4(立方厘米)
答:圆柱的高是10厘米,长方体的体积是502.4立方厘米。
【要点提升】抓住圆柱切成若干等分,拼成一个近似的长方体的方法,得出表面积中增加的是以圆柱的高和半径为边长的长方形的面积,是解决此类问题的关键。
33.六(1)班植树80棵;六(2)班植树48棵;六(3)班植树72棵。
【精讲精析】把总棵数看成单位“1”,六(1)班植树棵数占总棵数的40%,六(2)班和六(3)班植树的总棵数就占60%;六(2)班和六(3)班植树棵数的比是2∶3,那么六(2)班的棵数就是两个班棵数的;用60%乘就是六(2)植树占总棵数的百分之几;同理求出六(3)班占总棵数的百分之几;再求出六(1)班比六(2)班多植总棵数的几分之几它对应的数量是32棵,由此用除法求出总棵数,进而求出三个班植树的棵数。
【解题思路】由分析可得:六(2)班和六(3)班植树棵数的比是2∶3,那么六(2)班的棵数就是两个班棵数的;六(3)班的棵数就是两个班棵数的;
(1-40%)×
=60%×
=24%
(1-40%)×
=60%×
=36%
32÷(40%-24%)
=32÷16%
=200(棵)
六(1)班植树的棵树:200×40%=80(棵)
六(2)班植树的棵树:200×24%=48(棵)
六(3)班植树的棵树:200×36%=72(棵)
答:六(1)班植树80棵,六(2)班植树48棵,六(3)班植树72棵。
【要点提升】解答此类问题,首先找清单位“1”,根据乘法的意义求出六(2)班和六(3)班植树棵数是总数的百分之几;求单位“1”的百分之几用乘法;已知单位“1”的百分之几是多少,求单位“1”用除法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初重点中学择校分班预测卷
一、选择题
1.10克糖溶解在100克水中,糖和糖水重量的比是( )。
A.11∶1 B.1∶11 C.1∶10 D.1∶12
2.下面直线上点P表示的数是( )。
A.﹣2.5 B.﹣1.5 C.﹣0.5 D.1.5
3.如图中,正方形的边长都是10cm。请你比较一下,如图各图阴影部分面积和左边第一个阴影部分面积相等的有( )个。
A.1个 B.2个 C.3个 D.4个
4.九月份用水比八月份节约了9%,也就是九月份用水是八月份的( )。
A.109% B.91% C.9% D.无法判断
5.A÷3=B×7,A和B的最简整数比是( )。
A.3∶7 B.21∶1 C.7∶3
6.把一个圆柱的侧面展开,不可能是( )。
A.长方形 B.正方形 C.平行四边形 D.梯形
7.一张边长为4分米的正方形纸,如果在这张纸上剪4个相等并且最大的圆,4个圆的面积和是这张纸的( ).
A.78.5% B.80% C.75%
二、填空题
8.0.55∶的比值是( ),( )公顷比15公顷多20%。
9. ÷12= ∶ == %。
10.甘肃省海拔最低处是陇南白龙江中游文县罐子沟,海拔是550米,记作﹢550米,中国海拔最低处是新疆艾丁湖,低于海平面154.21米,记作( )米。
11.甲数是乙数的60%,甲数比乙数少 % ,乙数比甲数多 % .
12.在比例式7:2=21:6中,如果第一个比的后项加上6,那么第二个比的后项要加上 等式才成立.
13.等底等高的圆柱和圆锥的体积相差16立方分米,这个圆柱的体积是( )。
14.( )÷20==( )∶4=( )%=1.25。
15.用小棒摆五边形,如下图所示。
按照这样的方法继续摆下去,摆第5幅图需要( )根小棒,摆第n幅图需要( )根小棒。
三、判断题
16.把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的。( )
17.圆柱的体积是圆锥体积的。( )
18.,,,,……这列数越来越接近0. ( )
19.小麦每公顷产量一定,小麦的总产量与公顷数成反比例。( )
20.4,,0.5,这四个数能组成比例. ( )
21.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒。( )
四、计算题
22.直接写得数。
60×20= 0÷36= 7.2+2.87= 908-303≈
25×4%= 5÷×4 =
23.计算下面各题,能简算的要简算.
×15.31+×2.69 24×+76÷5 14.25-2.83-0.17
375+450÷18×25 [×(-)]÷
24.解方程或比例。
x÷6=48% x-8=20 ∶x=∶9
25.求总支出是多少元?
五、作图题
26.按要求作图
(1)过C点作AB边上的垂线,垂足为D,点D的位置用数对表示是( , )。
(2)画出三角形ABC绕B点逆时针旋转90度后的图形。
(3)在合适的位置画出三角形ABC按2∶1的比放大后的图形。
六、解答题
27.小萱在学校踢毽子比赛中踢了60个。她踢毽子的数量是小琳的。小琳踢了多少个?
28.爸爸想在网上书店买书,A店打七折,B店每满69元减19元。如果爸爸想买的书价为80元,在A、B两个书店买,在哪个书店购买合适?
29.将一个底面周长是18.84厘米、高是10厘米的圆柱形量杯里装满水,再倒入一个长12厘米、宽5厘米的长方体容器中,水面高是多少厘米?
30.王芳买了一听圆柱形易拉罐包装的饮料,侧面有“净含量320毫升”的字样,从饮料罐外面量,底面直径6厘米,高1.2分米。请问这家生产商是否欺骗消费者?
31.修一条公路,修了全长的后,离这条公路的中点还有1.7千米。这条公路全长多少千米?
32.如图所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加80平方厘米。
(1)同学们回忆圆柱体积计算公式的推导过程,用自己喜欢的方式将它记录下来。
(2)那么圆柱的高是多少厘米?长方体的体积是多少立方厘米?
33.六年级三个班级同学植树,六(1)班植树棵数占总棵数的40%,六(2)班、六(3)班植树棵数的比是2∶3,六(1)班比六(2)班多植树32棵。三个班种树多少棵?
答案与解析
1.B
【精讲精析】已知10克糖溶解在100克水中,则糖水的重量是(10+100)克;根据比的意义写出糖和糖水的重量比,并化简比。
【解题思路】10∶(10+100)
=10∶110
=(10÷10)∶(110÷10)
=1∶11
糖和糖水重量的比是1∶11。
故答案为:B
2.C
【精讲精析】直线上点P表示的数是0和﹣1的中点,即﹣0.5,也可以用(1+0)÷2来计算,再加上负号即可。
【解题思路】下面直线上点P表示的数是﹣0.5。
故答案为:C
【要点提升】此题主要考查负数的意义和数轴的认识。
3.D
【精讲精析】正方形面积公式S正=a2(a为边长),圆的面积公式S圆=πr2,据此分别计算出每个图形的面积再比较。
【解题思路】计算第一个图形阴影部分面积:
第一个图形中,正方形边长为10cm,圆的直径等于正方形边长10cm,半径r=10÷2=5cm。根据正方形面积S正=10×10=100cm2;圆的面积S圆=π×52= 25πcm2,那么阴影部分面积S1=100-25πcm2。
计算第二个图形阴影部分面积:
第二个图形中,扇形半径等于正方形边长10cm ,扇形面积S扇=πr2=π×102=25πcm2,正方形面积是100cm2,阴影部分面积S2=100-25πcm2,与第一个图形阴影部分面积相等。
计算第三个图形阴影面积:
第三个图形中,4个小圆的直径为10÷2=5cm,半径r=5÷2=2.5cm。4个小圆的面积和S4圆=4×π×2.52=4×π×=25πcm2正方形面积是100cm2,阴影部分面积S3=100-25πcm2,与第一个图形阴影部分面积相同。
计算第四个图形阴影面积:
第四个图形中,把图形中空白部分拼合起来,可得到一个半径为5cm的圆,其面积为25πcm2,正方形面积是100cm2 ,阴影部分面积S4=100-25πcm2 ,与第一个图形阴影部分面积相等。
计算第五个图形阴影面积。
第五个图形中,两个半圆可以拼成一个直径为10cm,半径为5cm的圆,圆的面积是25πcm2 ,正方形面积是100cm2 ,阴影部分面积S5=100-25πcm2,与第一个图形阴影部分面积相等。
综上分析所述,如图各图阴影部分面积和左边第一个阴影部分面积相等的有4个。
故答案为:D
4.B
【精讲精析】分析题目,把八月份的用水量看作单位“1”,则九月份的用水量是(1-9%),根据求一个数是另一个数的百分之几是多少用除法用九月份的用水量除以八月份的用水量即可解答。
【解题思路】假设八月份的用水量是1,则九月份的用水量是1-9%=91%。
91%÷1=91%
九月份用水比八月份节约了9%,也就是九月份用水是八月份的91%。
故答案为:B
5.B
【精讲精析】假设结果是1,根据除法和乘法各部分之间的关系,分别求出A和B,写出A和B的比,化简即可。
【解题思路】(1×3)∶(1÷7)
=3∶
=21∶1
故答案为:B
【要点提升】两数相除又叫两个数的比,化简比根据比的基本性质。
6.D
【精讲精析】圆柱的展开图可能是正方形、可能是长方形、也可能是平行四边形,根据圆柱的侧面展开图的特点,结合圆柱的侧面的几种展开图方法与展开图的特点即可进行选择。
【解题思路】圆柱的侧面沿高展开可能是长方形或正方形,如果斜着展开是一个平行四边形,因为圆柱的上下底面是完全相同的两个圆,所以圆柱的侧面展开图不可能是梯形。
故答案为:D
7.A
8. 1.1 18
【精讲精析】求比值,用前项除以后项即可;
把15公顷看成单位“1”,要求的面积比15公顷多20%,先用15公顷乘20%,求出多的部分,再加上15公顷即可。
【解题思路】0.55÷=1.1
15×20%+15
=3+15
=18(公顷)
【要点提升】本题考查了求比值以及求比一个数多百分之几的数是多少,只要找清单位“1”,利用基本数量关系解决问题。
9. 9 3 4 75
【精讲精析】根据分数与比、分数与除法的关系:=3∶4=3÷4,根据商不变的性质,被除数和除数同时乘3,分子除以分母。完成填空即可。
【解题思路】9÷12=3∶4==75%
【要点提升】解答此题的关键,根据小数、百分数、除法、比之间的关系及商不变的性质、比的基本性质即可进行转化。
10.﹣154.21
【精讲精析】通常把海平面的高度记作0,高出海平面记作“﹢”,低于海平面记作“﹣”。
【解题思路】由分析可知:
低于海平面154.21米,记作﹣154.21米。
【要点提升】本题是考查正、负数的意义及其应用。
11. 40 66.7
【精讲精析】把乙数看作单位“1”,则甲数为60%,则甲数比乙数少(1﹣60%);求乙数比甲数多几分之几,把甲数看作单位“1”,根据“(大数﹣小数)÷单位“1”的量”进行解答.
【解题思路】1﹣60%=40%;
(1﹣60%)÷60%,
=40%÷60%,
≈66.7%
故答案为40,66.7.
12.18
【解题思路】试题分析:第一个比的后项加6后变成7:8,要想使等式成立,就要让第二个比的最简比也应变成7:8,根据比的基本性质,7:8=(7×3):(8×3)=21:24,即第二个比的后项6加上18变成24,21:(6+18)=21:24=7:8,所以第二个比的后项应该加18才能使比例成立.
解答:解:7:(2+6)=7:8,
又7:8=(7×3):(8×3)=21:24
即需第二个比的后项6加上24﹣6=18,
所以第二个比的后项应该加18才能使比例成立;
故答案为18.
点评:完成本题要注意比值和原来不一样了,变化不是倍数关系.
13.24立方分米/24dm3
【精讲精析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,可以把圆锥的体积看作1份,则圆柱的体积是3份,相差(3-1)份;用等底等高的圆柱和圆锥的体积之差除以份数差,求出一份数,即是圆锥的体积,再乘3,就是这个圆柱的体积。
【解题思路】圆锥的体积:
16÷(3-1)
=16÷2
=8(立方分米)
圆柱的体积:
8×3=24(立方分米)
【要点提升】明确等底等高的圆柱与圆锥的体积关系,利用差倍问题的解题方法解答。
14.25;16;5;125
【精讲精析】根据比和百分数、分数、小数的关系,以及比和分数、除法的关系,分析填空即可。
【解题思路】因为4×1.25=5,5∶4==25÷20,1.25=125%,
所以25÷20==5∶4=125%=1.25。
【要点提升】本题考查了比和百分数、分数、小数的互化,属于综合性基础题,计算时需细心。
15. 21 4n+1
【精讲精析】第1幅图需要的小棒数为5根,即:4×1+1;第2幅图需要的小棒数为9根,即::4×2+1;第3幅图需要的小棒数为13根,即:4×3+1;……第n幅图需要的小棒数为: 4n+1;据此填空即可。
【解题思路】根据分析可得:
4×5+1
=20+1
=21(个)
所以,按照这样的方法继续摆下去,摆第5幅图需要21根小棒,摆第n幅图需要(4n+1)根小棒。
【要点提升】本题主要考查数与形结合的规律,发现每多1个幅图就多4根小棒是解本题的关键。
16.×
【精讲精析】根据题意,把一个圆柱削成一个圆锥,如果削成的圆锥与圆柱等底等高,那么圆锥的体积是圆柱体积的;如果削成的圆锥与圆柱不是等底等高,那么圆锥的体积就不是圆柱体积的;据此判断。
【解题思路】把一个圆柱削成一个与它等底等高的圆锥,这个圆锥的体积才是圆柱体积的。
原题说法错误。
故答案为:×
【要点提升】明确等底等高的圆柱和圆锥体积之间的关系是解题的关键。
17.×
18.√
【解题思路】,,,,……这个数列第一个数是,后面的数依次是前面一个数除以2的结果,因此分子1不变,分母从3开始以2倍的速度扩大,所以这列数越来越接近0.该说法正确.
19.×
【精讲精析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解题思路】小麦的总产量÷公顷数=小麦每公顷产量(一定),商一定,所以小麦每公顷产量成正比例。
故答案为:×
【要点提升】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
20.√
【解题思路】略
21.√
【精讲精析】规律:小棒的根数=小正方形的个数×3+1,根据这样的规律计算后做出判断即可。
【解题思路】摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
………
所以摆n个正方形要小棒:4+3×(n-1)=3n+1(根);
n=10,3×10+1=31(根);摆10个正方形一共需要31根小棒,原题说法正确。
故答案为:√
22.1200;0;10.07;600
1;;1;100
23.15; 20; 11.25;
1000;
24.x=2.88;x=35;x=24
【精讲精析】“x÷6=48%”将等式两边同时乘6,解出x;
“x-8=20”将等式两边同时加上8,再同时除以,解出x;
“∶x=∶9”先将比例写成一般方程,再将等式两边同时除以,解出x。
【解题思路】x÷6=48%
解:x=48%×6
x=2.88
x-8=20
解:x=20+8
x=28÷
x=35
∶x=∶9
解:x=9×
x=6÷
x=24
25.6200元
【精讲精析】根据图意可知,把总支出看作单位“1”,根据百分数除法的意义,用食品支出比其它支出多的钱数(620元)除以多占总支出的百分率(55%-45%)就是总支出。
【解题思路】620÷(55%-45%)
=620÷10%
=6200(元)
答:总支出是6200元。
【要点提升】此题是考查百分数除法的意义及应用。已知一个数的百分之几是多少,求这个数,用已知数除以它所对应的分率。
26.(1)画图见详解;(1,6)
(2)和(3)见详解
【精讲精析】(1)延长BA,再过C点向延长线上做垂线即可;数对中第一个数字表示列,第二个数字表示行,由此写出点D的位置即可;
(2)根据旋转的方法,将三角形与点B相连的两条边绕点B逆时针旋转90度,再将其它边连起来即可;
(3)将三角形ABC按2∶1的比放大,则放大后三角形的边长是原三角形的2倍,据此画图即可。
【解题思路】
点D的位置用数对表示是(1,6)。
【要点提升】本题综合性较强,熟练掌握数对表示位置的特点,图形旋转的方法以及图形放大与缩小的方法是解答本题的关键。
27.80个
【精讲精析】把小琳踢毽子的数量看作单位“1”,小萱踢毽子的数量是小琳的,对应的是小萱踢毽子的数量60个,求单位“1”,用60÷解答。
【解题思路】60÷
=60×
=80(个)
答:小琳踢了80个。
28.A店
【精讲精析】把在两家书店购买的价格算出来再比较,便宜的更合适:
A店:七折就是70%,把原价看作单位“1”,根据求一个数的百分之几是多少,用乘法计算。
B店:先用80除以69所得的商再乘19可得可减几元,最后用80减几即可得购买的价格。
【解题思路】A店:80×70%=56(元)
B店:
80-19×1
=80-19
=61(元)
56<61
答:到A店买更合适。
29.4.71厘米
【精讲精析】先求圆柱形容积,因为这部分水全部倒入了长方体容器中,所以用这部分体积去除长方体的底面积,可得到水面高度。
【解题思路】
=32×3.14×10÷60
=282.6÷60
=4.71(厘米)
答:水面高度是4.71厘米。
【要点提升】本题属于体积的等积变形,利用水的形状改变前后体积是不变的,确定改变后的体积,再计算出改变后的水的高度。
30.没有欺骗
【精讲精析】根据圆柱的体积公式:底面积×高,求出这个圆柱形易拉罐的体积,再和包装上的“净含量320毫升”比较,即可解答。
【解题思路】1.2分米=12厘米 320毫升=320立方厘米
圆柱体体积为3.14×(6÷2)2×12
=3.14×9×12
=339.12(立方厘米)
339.12立方厘米=339.12毫升
339.12>320
没有欺骗消费者。
答:这家生产商家没有欺骗消费者。
【要点提升】本题考查圆柱体的面积公式的应用;关键是熟记公式。
31.23.8千米
【精讲精析】把这条公路长度看作单位“1”,这条公路的中点就是公路长度的处,修了全长的后,再修全长的(-),也就是1.7千米占总长度的对应分率,根据部分数量÷对应分率=整体数量,列式解答即可。
【解题思路】1.7÷(-)
=1.7÷
=1.7×14
=23.8(千米)
答:这条公路全长23.8千米。
32.(1)把圆柱底面平均分成若干等份的小扇形,沿圆柱的高切开,拼成一近似的长方体。发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,长方体的体积等于底面积乘高,所以圆柱的体积也等于底面积乘高。若体积用字母V表示,底面积用字母S表示,高用h表示,即体积为:V=Sh;
(2)10厘米;502.4立方厘米
【精讲精析】(1)根据圆柱体积计算公式的推导过程解答即可;
(2)圆柱切成若干等分,拼成一个近似的长方体后,表面积比原来的圆柱的表面积增加了两个以圆柱的高和半径为边长的长方形的面积,体积与原来圆柱的体积相等;据此解答。
【解题思路】(1)把圆柱底面平均分成若干等份的小扇形,沿圆柱的高切开,拼成一近似的长方体。发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,长方体的体积等于底面积乘高,所以圆柱的体积也等于底面积乘高。若体积用字母∨表示,底面积用字母S表示,高用h表示,即体积为:V=Sh。
(2)80÷2÷(8÷2)
=40÷4
=10
3.14×(8÷2)2×10
=3.14×160
=502.4(立方厘米)
答:圆柱的高是10厘米,长方体的体积是502.4立方厘米。
【要点提升】抓住圆柱切成若干等分,拼成一个近似的长方体的方法,得出表面积中增加的是以圆柱的高和半径为边长的长方形的面积,是解决此类问题的关键。
33.六(1)班植树80棵;六(2)班植树48棵;六(3)班植树72棵。
【精讲精析】把总棵数看成单位“1”,六(1)班植树棵数占总棵数的40%,六(2)班和六(3)班植树的总棵数就占60%;六(2)班和六(3)班植树棵数的比是2∶3,那么六(2)班的棵数就是两个班棵数的;用60%乘就是六(2)植树占总棵数的百分之几;同理求出六(3)班占总棵数的百分之几;再求出六(1)班比六(2)班多植总棵数的几分之几它对应的数量是32棵,由此用除法求出总棵数,进而求出三个班植树的棵数。
【解题思路】由分析可得:六(2)班和六(3)班植树棵数的比是2∶3,那么六(2)班的棵数就是两个班棵数的;六(3)班的棵数就是两个班棵数的;
(1-40%)×
=60%×
=24%
(1-40%)×
=60%×
=36%
32÷(40%-24%)
=32÷16%
=200(棵)
六(1)班植树的棵树:200×40%=80(棵)
六(2)班植树的棵树:200×24%=48(棵)
六(3)班植树的棵树:200×36%=72(棵)
答:六(1)班植树80棵,六(2)班植树48棵,六(3)班植树72棵。
【要点提升】解答此类问题,首先找清单位“1”,根据乘法的意义求出六(2)班和六(3)班植树棵数是总数的百分之几;求单位“1”的百分之几用乘法;已知单位“1”的百分之几是多少,求单位“1”用除法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
