北师大版九年级数学上册课件 第二章第1节认识一元二次方程(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学上册课件 第二章第1节认识一元二次方程(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-03 00:00:00 | ||
图片预览







文档简介
课件22张PPT。第二章 一元二次方程
2.1.1
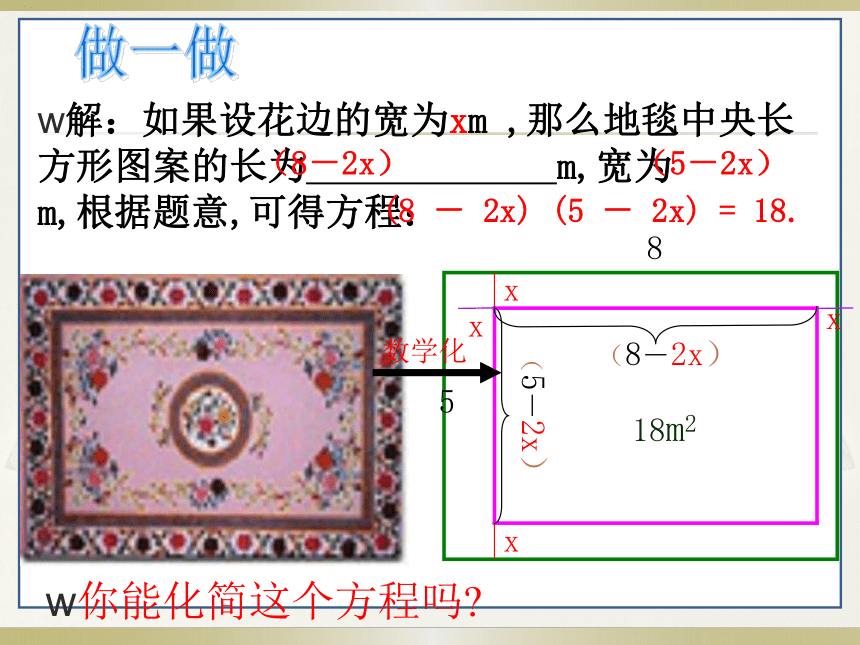
认识一元二次方程 幼儿园某教室矩形地面的墙长8m,宽5m现准备在地面中心铺设一块面积为18m2 的地毯,四周未铺地毯的条形区域的宽度相同,你能求出这个宽度吗?你怎么解决这个问题?数学与生活解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:你能化简这个方程吗? (8-2x)(5-2x) (8 - 2x) (5 - 2x) = 18.5xxxx (8-2x)(5-2x)818m2做一做观察下面等式:102+112+122=132+142 你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗? 如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为:根据题意,可得方程: , , , . X+1X+2X+3X+4想一想如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?解:由勾股定理可知,滑动前梯子底端距墙 m.
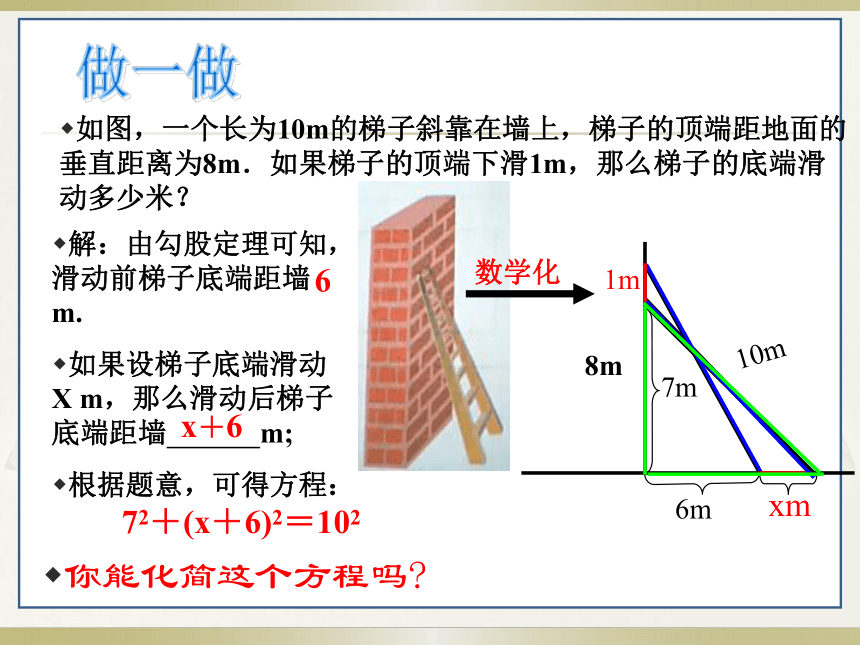
如果设梯子底端滑动X m,那么滑动后梯子底端距墙 m;
根据题意,可得方程:你能化简这个方程吗?6x+672+(x+6)2=102xm8m10m7m6m1m做一做 上面的方程都是只含有 的 ,并且都可以化为 的形式,这样的方程叫做一元二次方程.由上面两个问题,我们可以得到两个方程:把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别称为二次项、一次项和常数项,a, b分别称为二次项系数和一次项系数.(8-2x)(5-2x)=18;即2x2 - 13x +11=0(x+6)2+72=102即x2 +12 x -15=0上述两个方程有什么共同特点?一个未知数x整式方程ax2+bx+c=0(a,b,c为常数, a≠0)X2 +(X+1)2+(X+2)2=
即 x2 - 8x - 20=0(X+3)2+( X+4)2判一判 下列方程哪些是一元二次方程?(1)7x2-6x=0(2)2x2-5xy+6y=0(3)2x2- -1 =0 (4) =0(5)x2+2x-3=1+x2解: (1)、 (4) 把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:方 程一般形式二次项
系 数一次项
系 数常数项
3x2=5x-1(x+2)(x -1)=64-7x2=03x2-5x+1=0x2 +x-8=0-7x2 +0 x+4=03
1
-7-51
0 1-8 4练一练1.关于x的方程(k-3)x2 + 2x-1=0,当k 时,是一元二次方程.≠32.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,当k 时,是一元二次方程.,当k 时,是一元一次方程.≠±1=-1想一想:3、写出方程
的二次项系数、一次相系数和常数项。4、把方程(3x+2)2=4(x-3)2化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.5、从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.4尺2尺xx-4x-2随堂练习: 练习6.根据题意,列出方程:(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少? 解:设正方形的边长为xm,则原长方形的长为(x+5) m,宽为(x+2) m,依题意得方程: (x+5) (x+2) =54解:设第一个数为X,则另两个数分别为X+1 , X+2,依题意得方程:x (x+1) + x(x+2) + (x+1) (x+2) =242即x2 + 7x-44 =0即3x2 +6x-24 0=0x2 +2x-8 0=0在这个问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,把这个方程化为一般形式为x2+12x-15=0 .
(1)小明认为底端也滑动了1m,他的说法正确吗?为什么?
(2)底端滑动的距离可能是2m吗?可能是3m吗?为什么? 不正确,因为x=1不满足方程.不正确,因为x=2,3不满足方程.(3)你能猜出滑动距离x(m)的大致范围吗?
(4)x的整数部分是几?十分位部分是几?
请同学们自己算一算,注意组内同学交流哦!下面是小亮的求解过程:由此,他猜测1<x<1.5.进一步计算:所以1.1<x<1.2,由此他猜测x整数部分是1,十分位部分是1.你的结果是怎样的呢?用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据. 【规律方法】上述求解是利用了“两边夹”的思想五个连续整数,前三个数的平方和等于后两个数的平方和。你能求出这五个整数分别是多少吗?【跟踪训练】A同学的做法:
设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意,可得方程:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
即:x2-8x-20=0.所以x=-2或10.因此这五个连续整数依次为-2, -1,0,1,2;或10,11,12,13,14.B同学的做法:
设五个连续整数中的中间一个数为x,那么其余四个数
依次可表示为x-2,x-1,x+1,x+2.根据题意,可得方程:(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2
即:x2-12x=0.所以x=0或12.因此这五个连续整数依次为-2,-1,0,1,2;或10,11,12,13,14.7.一名跳水运动员进行10米跳台跳水训练,在正常情况下,运动员必须在距水面5米以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误。假设运动员起跳后的运动时间t(秒)和运动员距水面的高度h(米)满足关系:h=10+2.5t-5t2,那么他最多有多长时间完成规定动作?
【解析】根据题意,得10+2.5t-5t2=5,即 2t2-t-2=0列表:所以1<t<2,进一步列表计算:所以1.2<t<1.3,因此他完成动作的时间最多不超过1.3秒.3.学习了估算ax2+bx+c=0(a,b,c为常数,a≠0)近似解的方法:“两边夹”;
4.知道了估算的步骤;
(1)先确定大致范围
(2)再取值计算,逐步逼近
5.想一想:有没有更便捷的方法求一元二次方程的解呢?
1.学习了什么是一元二次方程,以及它的一般形式ax2+bx+c=0(a,b,c为常数,a≠0)和有关概念,如二次项、一次项、常数项、二次项系数、一次项系数.
2.会用一元二次方程表示实际生活中的数量关系.
小结
2.1.1
认识一元二次方程 幼儿园某教室矩形地面的墙长8m,宽5m现准备在地面中心铺设一块面积为18m2 的地毯,四周未铺地毯的条形区域的宽度相同,你能求出这个宽度吗?你怎么解决这个问题?数学与生活解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:你能化简这个方程吗? (8-2x)(5-2x) (8 - 2x) (5 - 2x) = 18.5xxxx (8-2x)(5-2x)818m2做一做观察下面等式:102+112+122=132+142 你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗? 如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为:根据题意,可得方程: , , , . X+1X+2X+3X+4想一想如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?解:由勾股定理可知,滑动前梯子底端距墙 m.
如果设梯子底端滑动X m,那么滑动后梯子底端距墙 m;
根据题意,可得方程:你能化简这个方程吗?6x+672+(x+6)2=102xm8m10m7m6m1m做一做 上面的方程都是只含有 的 ,并且都可以化为 的形式,这样的方程叫做一元二次方程.由上面两个问题,我们可以得到两个方程:把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别称为二次项、一次项和常数项,a, b分别称为二次项系数和一次项系数.(8-2x)(5-2x)=18;即2x2 - 13x +11=0(x+6)2+72=102即x2 +12 x -15=0上述两个方程有什么共同特点?一个未知数x整式方程ax2+bx+c=0(a,b,c为常数, a≠0)X2 +(X+1)2+(X+2)2=
即 x2 - 8x - 20=0(X+3)2+( X+4)2判一判 下列方程哪些是一元二次方程?(1)7x2-6x=0(2)2x2-5xy+6y=0(3)2x2- -1 =0 (4) =0(5)x2+2x-3=1+x2解: (1)、 (4) 把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:方 程一般形式二次项
系 数一次项
系 数常数项
3x2=5x-1(x+2)(x -1)=64-7x2=03x2-5x+1=0x2 +x-8=0-7x2 +0 x+4=03
1
-7-51
0 1-8 4练一练1.关于x的方程(k-3)x2 + 2x-1=0,当k 时,是一元二次方程.≠32.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,当k 时,是一元二次方程.,当k 时,是一元一次方程.≠±1=-1想一想:3、写出方程
的二次项系数、一次相系数和常数项。4、把方程(3x+2)2=4(x-3)2化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.5、从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.4尺2尺xx-4x-2随堂练习: 练习6.根据题意,列出方程:(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少? 解:设正方形的边长为xm,则原长方形的长为(x+5) m,宽为(x+2) m,依题意得方程: (x+5) (x+2) =54解:设第一个数为X,则另两个数分别为X+1 , X+2,依题意得方程:x (x+1) + x(x+2) + (x+1) (x+2) =242即x2 + 7x-44 =0即3x2 +6x-24 0=0x2 +2x-8 0=0在这个问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,把这个方程化为一般形式为x2+12x-15=0 .
(1)小明认为底端也滑动了1m,他的说法正确吗?为什么?
(2)底端滑动的距离可能是2m吗?可能是3m吗?为什么? 不正确,因为x=1不满足方程.不正确,因为x=2,3不满足方程.(3)你能猜出滑动距离x(m)的大致范围吗?
(4)x的整数部分是几?十分位部分是几?
请同学们自己算一算,注意组内同学交流哦!下面是小亮的求解过程:由此,他猜测1<x<1.5.进一步计算:所以1.1<x<1.2,由此他猜测x整数部分是1,十分位部分是1.你的结果是怎样的呢?用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据. 【规律方法】上述求解是利用了“两边夹”的思想五个连续整数,前三个数的平方和等于后两个数的平方和。你能求出这五个整数分别是多少吗?【跟踪训练】A同学的做法:
设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意,可得方程:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
即:x2-8x-20=0.所以x=-2或10.因此这五个连续整数依次为-2, -1,0,1,2;或10,11,12,13,14.B同学的做法:
设五个连续整数中的中间一个数为x,那么其余四个数
依次可表示为x-2,x-1,x+1,x+2.根据题意,可得方程:(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2
即:x2-12x=0.所以x=0或12.因此这五个连续整数依次为-2,-1,0,1,2;或10,11,12,13,14.7.一名跳水运动员进行10米跳台跳水训练,在正常情况下,运动员必须在距水面5米以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误。假设运动员起跳后的运动时间t(秒)和运动员距水面的高度h(米)满足关系:h=10+2.5t-5t2,那么他最多有多长时间完成规定动作?
【解析】根据题意,得10+2.5t-5t2=5,即 2t2-t-2=0列表:所以1<t<2,进一步列表计算:所以1.2<t<1.3,因此他完成动作的时间最多不超过1.3秒.3.学习了估算ax2+bx+c=0(a,b,c为常数,a≠0)近似解的方法:“两边夹”;
4.知道了估算的步骤;
(1)先确定大致范围
(2)再取值计算,逐步逼近
5.想一想:有没有更便捷的方法求一元二次方程的解呢?
1.学习了什么是一元二次方程,以及它的一般形式ax2+bx+c=0(a,b,c为常数,a≠0)和有关概念,如二次项、一次项、常数项、二次项系数、一次项系数.
2.会用一元二次方程表示实际生活中的数量关系.
小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
