北京市延庆区2024-2025学年第二学期八年级期末数学试卷(PDF版,无答案)
文档属性
| 名称 | 北京市延庆区2024-2025学年第二学期八年级期末数学试卷(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 498.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 10:50:18 | ||
图片预览


文档简介
延庆区 2024-2025 学年第二学期期末试卷
八 年 级 数 学 2025.06
考 1.本试卷共 7页,共三道大题,28道小题,满分 100分,考试时间 120分钟.
生 2.在试卷和答题卡上正确填写学校名称、姓名和考号.
须 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
知 4.在答题卡上,选择题、作图题用 2B铅笔作答,其他试题用黑色签字笔作答.
一、选择题(共 16 分,每小题 2 分)
第 1-8 题均有四个选项,符合题意的选项只有一个.
1.下列图形中,既是轴对称图形又是中心对称图形的是
等边三角形 平行四边形 矩形 正五边形
(A) (B) (C) (D)
2.一元二次方程 2x2+3x 4=0的一次项系数是
(A)2 (B)3 (C)4 (D)
3.如果 x=1是关于 x的方程 x2 3x+m=0的一个根,那么实数 m的值为
(A) (B)4 (C)1 (D)2
4.在平面直角坐标系 xOy中,点 A(2,3)关于 x轴的对称点的坐标是
(A)(2,3) (B)(2, 3) (C)( 2,3) (D)( 2, 3)
5.六边形的外角和为
(A)360° (B)540° (C)720° (D)900°
6.当关于 x的一元二次方程 kx2 2x+1=0有两个不相等的实数根时,k的取值范围是
(A)k<1 (B)k> 1
(C)k<1且 k≠0 (D)k> 1且 k≠0
八年级数学 第 1 页 共 7 页
7.下列命题是假.命.题.的是
(A)两组对边分别相等的四边形是平行四边形
(B)对角线相等的平行四边形是矩形
(C)对角线互相垂直的平行四边形是菱形
(D)对角线互相垂直且相等的四边形是正方形
8.如图,在平面直角坐标系 xOy中,y关于 x的函数图象与 x轴有且只有三个公共
点,坐标分别为( 3,0),( 1,0),(3,0).
关于该函数的四个结论如下:
①当 x>3时,y的取值范围是 y>0;
②当 y<0时,x的取值范围是 1③将该函数图象向左平移 3个单位长度后,
得到的函数图象经过原点;
④该函数图象上有且只有一个横坐标与纵坐标之和是 1的点.
其中正确的结论有
(A)1个 (B)2个 (C)3个 (D)4个
二、填空题(共 16 分,每小题 2 分)
9 2.函数 y 中自变量 x的取值范围是____________.
x 1
10.一元二次方程 x2 6x=0的解为____________.
11.一组数据“ 2,2,0,4”的方差为 s2,则 s2=____________.
12.如图,在□ABCD中,∠A+∠C=100°,则∠B=____________°. 第 12题图
13.写出一个图象经过第二、四象限的正比例函数的表达式____________.
14.已知点 A( 1, y1 )和 B(2, y2 )是一次函数 y=3x 2的图象上的两点,
则 y1 ________ y2 (填“>”或“<”).
15.在平面直角坐标系 xOy中,函数 y=2x+m与 y= x+n的图象交于点 P(1,4),
则关于 x的不等式 2x+m< x+n的解集是____________.
八年级数学 第 2 页 共 7 页
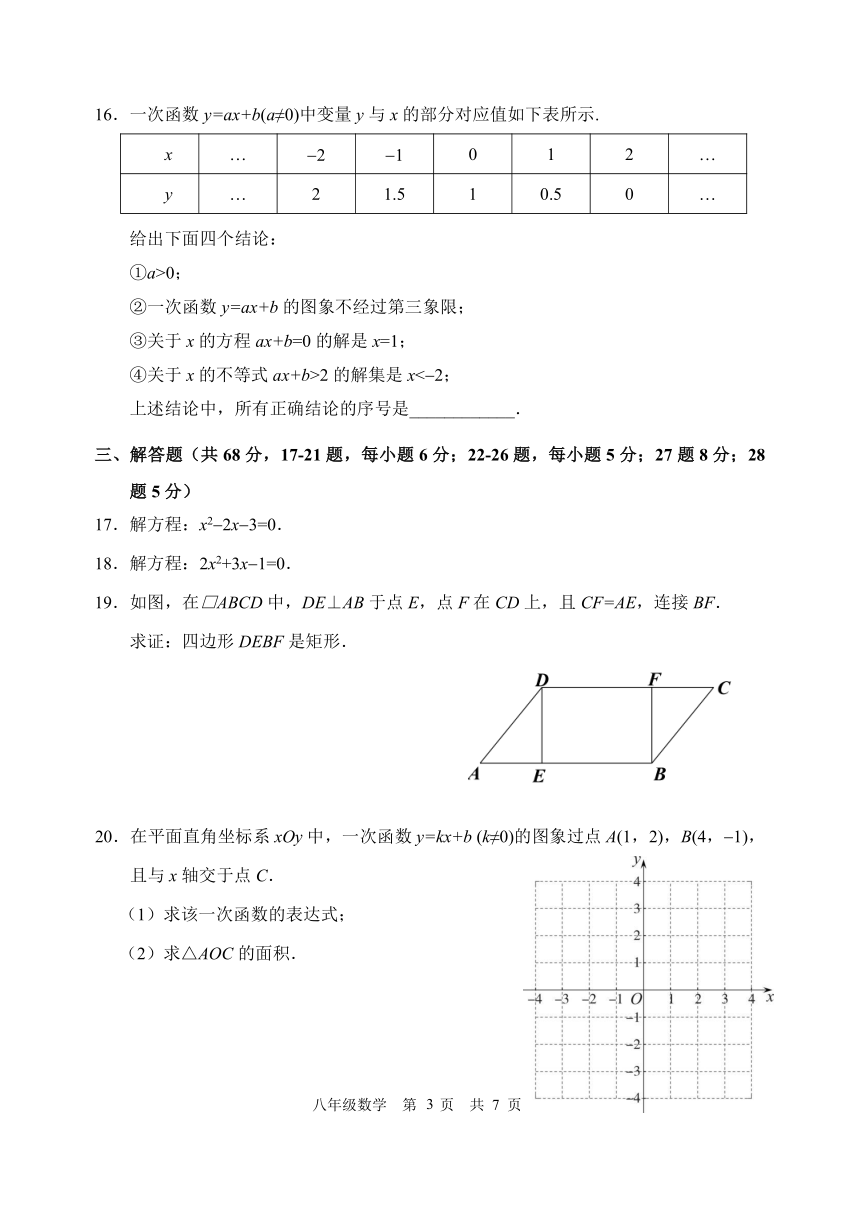
16.一次函数 y=ax+b(a≠0)中变量 y与 x的部分对应值如下表所示.
x … 2 1 0 1 2 …
y … 2 1.5 1 0.5 0 …
给出下面四个结论:
①a>0;
②一次函数 y=ax+b的图象不经过第三象限;
③关于 x的方程 ax+b=0的解是 x=1;
④关于 x的不等式 ax+b>2的解集是 x< 2;
上述结论中,所有正确结论的序号是____________.
三、解答题(共 68 分,17-21 题,每小题 6 分;22-26 题,每小题 5 分;27 题 8 分;28
题 5 分)
17.解方程:x2 2x =0.
18.解方程:2x2+3x 1=0.
19.如图,在□ABCD中,DE⊥AB于点 E,点 F在 CD上,且 CF=AE,连接 BF.
求证:四边形 DEBF是矩形.
20.在平面直角坐标系 xOy中,一次函数 y=kx+b (k≠0)的图象过点 A(1,2),B(4, 1),
且与 x轴交于点 C.
(1)求该一次函数的表达式;
(2)求△AOC的面积.
八年级数学 第 3 页 共 7 页
21.已知关于 x的一元二次方程 x2 5mx+4m2=0.
(1)求证:该方程总有两个实数根;
(2)若 m>0,且该方程的两个实数根的差为 6,求 m的值.
22.如图,矩形 ABCD的对角线 AC,BD交于点 O,AE∥BD,DE∥AC.
(1)求证:四边形 AODE是菱形;
(2)若 AB=6,AO=5,求菱形 AODE的面积.
23.在平面直角坐标系 xOy中,函数 y kx 2与 y x 2的图象交于点 A(3,m).
(1)求 k和 m的值;
(2)点 B(n,y1 )在函数 y x 2的图象上,BC⊥x轴交函数 y kx 2的图象于点 C,
点 C的纵坐标为 y2.若 y1 y2 4,直接写出 n的取值范围.
八年级数学 第 4 页 共 7 页
24.某科技公司通过引入 AI算法优化云计算资源调度,使服务器运行成本逐月下降.原
来单台服务器每月运行成本为 2500元,经过两个月的技术迭代后,单台服务器每月
运行成本降至 1600元.求单台服务器运行成本的月平均降低率.
25.为了提升学生的数学核心素养,激发学生学习数学的兴趣,某校组织了“数学节”
活动,设置了数学小游戏、作品展示、数学知识竞赛三个主题.在活动中,学校有
200名学生参加了数学知识竞赛,从中随机抽取 40名学生的成绩(百分制)数据,
整理并绘制了如下统计图表:
40名学生成绩的频数分布表 40名学生成绩的频数分布直方图
成绩 x(分) 频数 频率
50≤x<60 3 0.075
60≤x<70 a b
70≤x<80 14 0.350
80≤x<90 c 0.150
90≤x≤100 5 0.125
合计 40 1.000
根据以上信息,回答下列问题:
(1)表 1中 b的值为 ,c的值为 ;
(2)补全频数分布直方图;
(3)若对成绩不低于 80分的学生进行奖励,估计参加数学知识竞赛的 200名学生
中获得奖励的学生有 名.
八年级数学 第 5 页 共 7 页
26.在平面直角坐标系 xOy中,一次函数 y=ax+b (a≠0)的图象过点( 1, 2),
且平行于直线 y= 2x.
(1)求一次函数 y=ax+b (a≠0)的表达式;
(2)当 x> 1时,对于 x的每一个值,一次函数 y=kx+k 2 (k≠0)的值大于一次
函数 y=ax+b (a≠0)的值,且小于函数 y= 2x的值,直接写出 k的取值范围.
27.如图,在正方形 ABCD中,E为对角线 AC上一点,连接 BE,∠CBE=α(0°< α <45°),
过点 E作 EF⊥BE,交 DC的延长线于点 F,交 BC于点 G.
(1)求∠CFE的大小(用含α的式子表示);
(2)求证:BE=FE;
(3)连接 AF,点 M是 AF的中点,连接 EM,
①依题意补全图形;
②用等式表示线段 EM与 CF的数量关系,并证明.
八年级数学 第 6 页 共 7 页
28.在平面直角坐标系 xOy中,对于点 P和线段 MN,给出如下定义:
如果存在点 Q,使得以 MN为对角线的四边形 PMQN是平行四边形,则称点 Q是
点 P关于线段 MN的“关联点”.
已知 A(0,1),B( 1,0),C(2,1),D(3,2),E( 6,3),F(1,0),G(m,1).
(1)在点 D,E,F中,点 是点 B关于线段 AC的“关联点”;
(2)求点 O关于线段 AC的“关联点”的坐标;
(3)若点 F关于线段 AG的“关联点”在△DOE的内部,直接写出 m的取值范围.
八年级数学 第 7 页 共 7 页
八 年 级 数 学 2025.06
考 1.本试卷共 7页,共三道大题,28道小题,满分 100分,考试时间 120分钟.
生 2.在试卷和答题卡上正确填写学校名称、姓名和考号.
须 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
知 4.在答题卡上,选择题、作图题用 2B铅笔作答,其他试题用黑色签字笔作答.
一、选择题(共 16 分,每小题 2 分)
第 1-8 题均有四个选项,符合题意的选项只有一个.
1.下列图形中,既是轴对称图形又是中心对称图形的是
等边三角形 平行四边形 矩形 正五边形
(A) (B) (C) (D)
2.一元二次方程 2x2+3x 4=0的一次项系数是
(A)2 (B)3 (C)4 (D)
3.如果 x=1是关于 x的方程 x2 3x+m=0的一个根,那么实数 m的值为
(A) (B)4 (C)1 (D)2
4.在平面直角坐标系 xOy中,点 A(2,3)关于 x轴的对称点的坐标是
(A)(2,3) (B)(2, 3) (C)( 2,3) (D)( 2, 3)
5.六边形的外角和为
(A)360° (B)540° (C)720° (D)900°
6.当关于 x的一元二次方程 kx2 2x+1=0有两个不相等的实数根时,k的取值范围是
(A)k<1 (B)k> 1
(C)k<1且 k≠0 (D)k> 1且 k≠0
八年级数学 第 1 页 共 7 页
7.下列命题是假.命.题.的是
(A)两组对边分别相等的四边形是平行四边形
(B)对角线相等的平行四边形是矩形
(C)对角线互相垂直的平行四边形是菱形
(D)对角线互相垂直且相等的四边形是正方形
8.如图,在平面直角坐标系 xOy中,y关于 x的函数图象与 x轴有且只有三个公共
点,坐标分别为( 3,0),( 1,0),(3,0).
关于该函数的四个结论如下:
①当 x>3时,y的取值范围是 y>0;
②当 y<0时,x的取值范围是 1
得到的函数图象经过原点;
④该函数图象上有且只有一个横坐标与纵坐标之和是 1的点.
其中正确的结论有
(A)1个 (B)2个 (C)3个 (D)4个
二、填空题(共 16 分,每小题 2 分)
9 2.函数 y 中自变量 x的取值范围是____________.
x 1
10.一元二次方程 x2 6x=0的解为____________.
11.一组数据“ 2,2,0,4”的方差为 s2,则 s2=____________.
12.如图,在□ABCD中,∠A+∠C=100°,则∠B=____________°. 第 12题图
13.写出一个图象经过第二、四象限的正比例函数的表达式____________.
14.已知点 A( 1, y1 )和 B(2, y2 )是一次函数 y=3x 2的图象上的两点,
则 y1 ________ y2 (填“>”或“<”).
15.在平面直角坐标系 xOy中,函数 y=2x+m与 y= x+n的图象交于点 P(1,4),
则关于 x的不等式 2x+m< x+n的解集是____________.
八年级数学 第 2 页 共 7 页
16.一次函数 y=ax+b(a≠0)中变量 y与 x的部分对应值如下表所示.
x … 2 1 0 1 2 …
y … 2 1.5 1 0.5 0 …
给出下面四个结论:
①a>0;
②一次函数 y=ax+b的图象不经过第三象限;
③关于 x的方程 ax+b=0的解是 x=1;
④关于 x的不等式 ax+b>2的解集是 x< 2;
上述结论中,所有正确结论的序号是____________.
三、解答题(共 68 分,17-21 题,每小题 6 分;22-26 题,每小题 5 分;27 题 8 分;28
题 5 分)
17.解方程:x2 2x =0.
18.解方程:2x2+3x 1=0.
19.如图,在□ABCD中,DE⊥AB于点 E,点 F在 CD上,且 CF=AE,连接 BF.
求证:四边形 DEBF是矩形.
20.在平面直角坐标系 xOy中,一次函数 y=kx+b (k≠0)的图象过点 A(1,2),B(4, 1),
且与 x轴交于点 C.
(1)求该一次函数的表达式;
(2)求△AOC的面积.
八年级数学 第 3 页 共 7 页
21.已知关于 x的一元二次方程 x2 5mx+4m2=0.
(1)求证:该方程总有两个实数根;
(2)若 m>0,且该方程的两个实数根的差为 6,求 m的值.
22.如图,矩形 ABCD的对角线 AC,BD交于点 O,AE∥BD,DE∥AC.
(1)求证:四边形 AODE是菱形;
(2)若 AB=6,AO=5,求菱形 AODE的面积.
23.在平面直角坐标系 xOy中,函数 y kx 2与 y x 2的图象交于点 A(3,m).
(1)求 k和 m的值;
(2)点 B(n,y1 )在函数 y x 2的图象上,BC⊥x轴交函数 y kx 2的图象于点 C,
点 C的纵坐标为 y2.若 y1 y2 4,直接写出 n的取值范围.
八年级数学 第 4 页 共 7 页
24.某科技公司通过引入 AI算法优化云计算资源调度,使服务器运行成本逐月下降.原
来单台服务器每月运行成本为 2500元,经过两个月的技术迭代后,单台服务器每月
运行成本降至 1600元.求单台服务器运行成本的月平均降低率.
25.为了提升学生的数学核心素养,激发学生学习数学的兴趣,某校组织了“数学节”
活动,设置了数学小游戏、作品展示、数学知识竞赛三个主题.在活动中,学校有
200名学生参加了数学知识竞赛,从中随机抽取 40名学生的成绩(百分制)数据,
整理并绘制了如下统计图表:
40名学生成绩的频数分布表 40名学生成绩的频数分布直方图
成绩 x(分) 频数 频率
50≤x<60 3 0.075
60≤x<70 a b
70≤x<80 14 0.350
80≤x<90 c 0.150
90≤x≤100 5 0.125
合计 40 1.000
根据以上信息,回答下列问题:
(1)表 1中 b的值为 ,c的值为 ;
(2)补全频数分布直方图;
(3)若对成绩不低于 80分的学生进行奖励,估计参加数学知识竞赛的 200名学生
中获得奖励的学生有 名.
八年级数学 第 5 页 共 7 页
26.在平面直角坐标系 xOy中,一次函数 y=ax+b (a≠0)的图象过点( 1, 2),
且平行于直线 y= 2x.
(1)求一次函数 y=ax+b (a≠0)的表达式;
(2)当 x> 1时,对于 x的每一个值,一次函数 y=kx+k 2 (k≠0)的值大于一次
函数 y=ax+b (a≠0)的值,且小于函数 y= 2x的值,直接写出 k的取值范围.
27.如图,在正方形 ABCD中,E为对角线 AC上一点,连接 BE,∠CBE=α(0°< α <45°),
过点 E作 EF⊥BE,交 DC的延长线于点 F,交 BC于点 G.
(1)求∠CFE的大小(用含α的式子表示);
(2)求证:BE=FE;
(3)连接 AF,点 M是 AF的中点,连接 EM,
①依题意补全图形;
②用等式表示线段 EM与 CF的数量关系,并证明.
八年级数学 第 6 页 共 7 页
28.在平面直角坐标系 xOy中,对于点 P和线段 MN,给出如下定义:
如果存在点 Q,使得以 MN为对角线的四边形 PMQN是平行四边形,则称点 Q是
点 P关于线段 MN的“关联点”.
已知 A(0,1),B( 1,0),C(2,1),D(3,2),E( 6,3),F(1,0),G(m,1).
(1)在点 D,E,F中,点 是点 B关于线段 AC的“关联点”;
(2)求点 O关于线段 AC的“关联点”的坐标;
(3)若点 F关于线段 AG的“关联点”在△DOE的内部,直接写出 m的取值范围.
八年级数学 第 7 页 共 7 页
同课章节目录
