1.2《全等三角形》(含答案)苏科版八年级数学上册
文档属性
| 名称 | 1.2《全等三角形》(含答案)苏科版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-02 00:00:00 | ||
图片预览



文档简介
1.2《全等三角形》
一、单选题
1.下列各选项中的两个图形属于全等图形的是( )
A.B.C.D.
2.下列说法正确的是( )
A.形状相同的两个图形一定全等 B.两个三角形是全等图形
C.两个全等图形面积一定相等 D.两个正方形一定是全等图形
3.如图, AOC≌ DOB,点C和点B是对应顶点,则边的对应边是( )
A. B. C. D.
4.下列说法正确的是( )
①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积相等;
③面积相等的三角形全等;④周长相等的三角形全等
A.②③ B.③④ C.①② D.①②③
5.已知图中的两个三角形全等,则的度数是( ).
A. B. C. D.以上都有可能
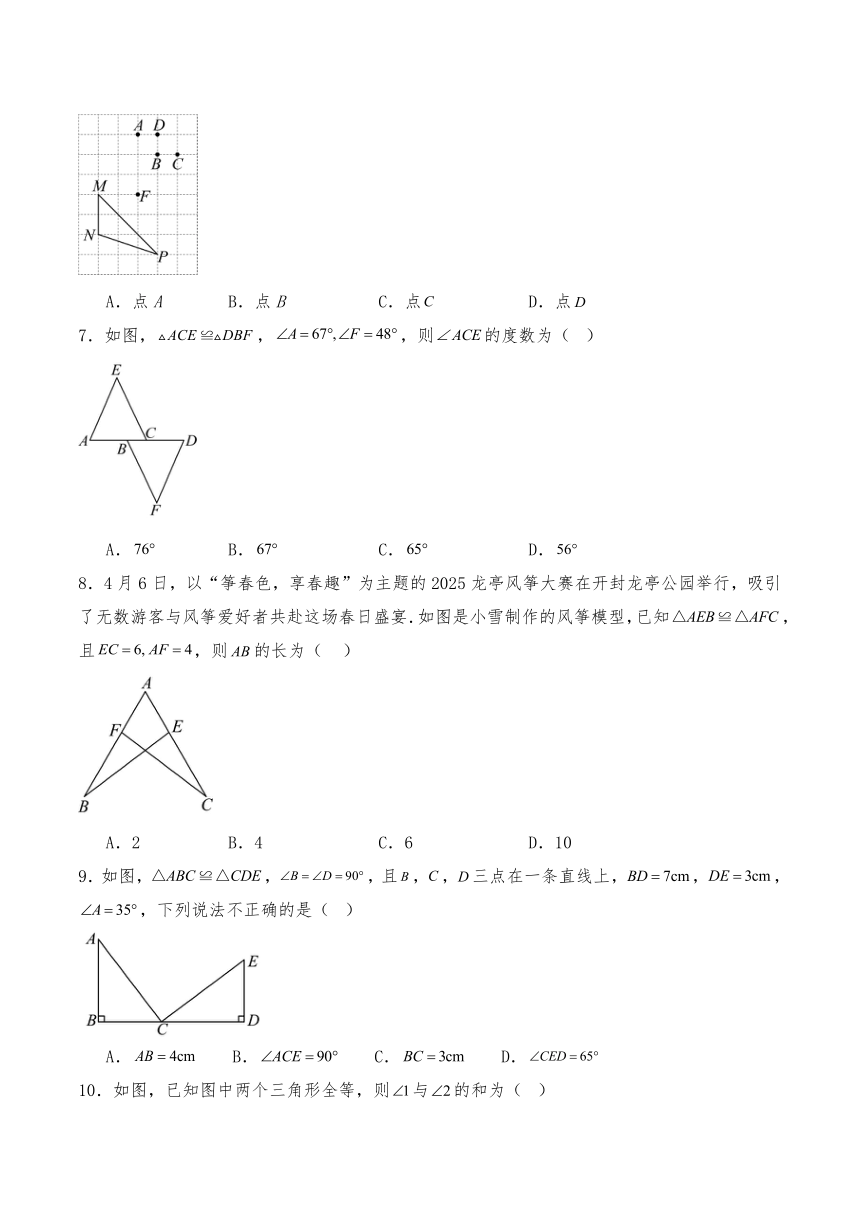
6.如图所示的网格中,每个小正方形的边长都相等,若,则点可能是图中的( )
A.点A B.点B C.点 D.点
7.如图,,,则的度数为( )
A. B. C. D.
8.4月6日,以“筝春色,享春趣”为主题的2025龙亭风筝大赛在开封龙亭公园举行,吸引了无数游客与风筝爱好者共赴这场春日盛宴.如图是小雪制作的风筝模型,已知,且,则的长为( )
A.2 B.4 C.6 D.10
9.如图,,,且,,三点在一条直线上,,,,下列说法不正确的是( )
A. B. C. D.
10.如图,已知图中两个三角形全等,则与的和为( )
A. B. C. D.
11.如图,四边形是由8个全等梯形拼接而成,其中,,则的长为( )
A.10.8 B.9.6 C.7.2 D.4.8
12.如图,,,三点共线,则下列结论中:①; ②;③;④;正确的有( )
A.1个 B.2个 C.3个 D.4个
13.如图所示,,下列四个结论中,不正确的是( )
A. B.,且
C.和的面积相等 D.和的周长相等
14.如图,在四边形中,,点为上的点(不与重合),观察下列图形中全等三角形的对数. 其中,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…. 按此规律,第5个图中有( )对全等三角形.
A.15 B.16 C.18 D.21
15.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1C1B1是全等(合同)三角形,且点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图①所示);若运动方向相反,则称它们是镜面合同三角形(如图②所示),两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个进行翻折.
下列各组合同三角形中,是镜面合同三角形的是( )
A. B. C. D.
二、填空题
16.如图,,,点在边上,则的度数为 .
17.如图,已知,并将它们摆成如图所示的形式,那么的度数等于 .
18.如图, BFD≌ CED,若的面积为,的面积为2,则的面积为 .
19.如图,在 ABC中,厘米,厘米,且,点D为的中点.如果点P在线段上以v厘米/秒的速度由B点向C点运动,同时,点在线段上由C点向A点运动.若点的运动速度为4厘米/秒,则当与 CQP全等时,v的值为 .
三、解答题
20.把如图所示的由16个小正方形组成的图形,用三种不同的方法沿网格线分割成两个全等图形.
21.如图,,连接,与交于点,,,.(1)求的度数;(2)求的度数.
22.如图,,且点B,D,C在一条直线上,点F在上,延长交于点E.(1)试说明:.(2)若,,求的长.
23.如图,在 ABC中,点、分别在边、上,连接、交于点,且.(1)求证:是等腰直角三角形;(2)若,,求四边形的面积.
24.如图,A,E,C三点在同一直线上,且.
(1)求证:;(2)猜想:当 ADE满足什么条件时?并证明你的猜想.
参考答案
一、单选题
1.C
【详解】解:A、两个图形不能完全重合,不是全等图形,故本选项不符合题意;
B、两个图形不能完全重合,不是全等图形,故本选项不符合题意;
C、两个图形能完全重合,是全等图形,故本选项符合题意;
D、两个图形不能完全重合,不是全等图形,故本选项不符合题意;故选:C.
2.C
【详解】解:A、形状相等的两个图形不一定全等,可能图形的大小不同,本选项说法错误;
B、两个三角形不一定全等,三角形的形状和大小不能确定,本选项说法错误;
C、两个全等的图形面积是一定相等的,本选项说法正确;
D、两个正方形不一定全等,因为两个正方形的边长可能不等,本选项说法错误;故选:C.
3.B
4.C
【详解】解:①全等三角形的对应边相等,对应角相等,正确;
②全等三角形的周长相等,面积相等,正确;③面积相等的三角形形状不一定相同,故错误;
④周长相等的三角形形状不一定相同,故错误.所以①②正确,故选:C.
5.A
【详解】解:由图可知:是边长为的边的一个邻角,∵两个三角形全等,∴;故选A.
6.D
【详解】解:∵,∴因点M、P在方格正方形的两个对角顶点上,故点M、Q也应在方格正方形的两个对角顶点上.所以点Q是图中点D的位置,如下图:故选:D.
,
7.C
【详解】解:∵,∴,
∴,故选:C.
8.D
【详解】解∶∵,,∴,,
∵,∴,故选∶D.
9.D
【详解】解:,
,,,,故选项C正确,不符合题意;
,;故选项A正确,不符合题意;
,,
故选项D错误,符合题意;故选项B正确,不符合题意;故选:D.
10.C
【详解】解:图中两个三角形全等,,,.故选:C.
11.B
【详解】解:∵四边形为梯形,上底,下底,四边形是由8个全等梯形拼接而成,∴.故选:B.
12.C
【详解】延长交于H,延长交于F,
∵,∴
∴,
∴,∴故①②正确,
∴,故③是错误的,
∵,∴,故④是正确的,故选:C.
13.A
【详解】解:∵,∴,,
∴,,故选项A不正确,符合题意;
,和的周长相等,和的面积相等,故选项B、C、D正确,不符合题意;故选:A.
14.D
【详解】解:根据题意,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…第个图中,有对全等三角形,
∴第5个图中有对全等三角形.故选:D.
15.B
【详解】根据真正合同三角形的定义可知,选项A,C,D是真正合同三角形,选项B是镜面合同三角形,
故选:B.
二、填空题
16.
【详解】解:∵,,∴∴,
∴,故答案为:.
17.
【详解】解:∵∴,
∴
由题意可得,,
又∵∴故答案为;
18.7
【详解】解:∵ BFD≌ CED,∴,,
∴,∴,故答案为:.
19.3或4
【详解】解:中,厘米,点为的中点,厘米,
若,则需厘米,(厘米),
点的运动速度为4厘米秒,点的运动时间为:,(厘米秒);
若 BPD≌ CQP,则需厘米,,,解得:;
的值为3或4.故答案为:3或4.
三、解答题
20.解:分割线如图所示:
21.(1)解:∵,∴,
∴,∴,∵,∴.
(2)解:∵,,,∴,,
∵,∴,
∴,由(1)已得:,
∴.
22.(1)证明:∵,∴,,
∵点B,D,C在一条直线上,∴,
∵,∴,∴;
(2)解:∵,∴,,
∵,∴,∴.
23.(1)证明:,,,
,,是等腰直角三角形;
(2)解:,,,
,,四边形的面积.
24.(1)解:∵,∴,,∴;
(2)解:猜想,时,,∵,∴,
∵,∴,∴,
又,∴,∴当 ADE是直角三角形时,.
一、单选题
1.下列各选项中的两个图形属于全等图形的是( )
A.B.C.D.
2.下列说法正确的是( )
A.形状相同的两个图形一定全等 B.两个三角形是全等图形
C.两个全等图形面积一定相等 D.两个正方形一定是全等图形
3.如图, AOC≌ DOB,点C和点B是对应顶点,则边的对应边是( )
A. B. C. D.
4.下列说法正确的是( )
①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积相等;
③面积相等的三角形全等;④周长相等的三角形全等
A.②③ B.③④ C.①② D.①②③
5.已知图中的两个三角形全等,则的度数是( ).
A. B. C. D.以上都有可能
6.如图所示的网格中,每个小正方形的边长都相等,若,则点可能是图中的( )
A.点A B.点B C.点 D.点
7.如图,,,则的度数为( )
A. B. C. D.
8.4月6日,以“筝春色,享春趣”为主题的2025龙亭风筝大赛在开封龙亭公园举行,吸引了无数游客与风筝爱好者共赴这场春日盛宴.如图是小雪制作的风筝模型,已知,且,则的长为( )
A.2 B.4 C.6 D.10
9.如图,,,且,,三点在一条直线上,,,,下列说法不正确的是( )
A. B. C. D.
10.如图,已知图中两个三角形全等,则与的和为( )
A. B. C. D.
11.如图,四边形是由8个全等梯形拼接而成,其中,,则的长为( )
A.10.8 B.9.6 C.7.2 D.4.8
12.如图,,,三点共线,则下列结论中:①; ②;③;④;正确的有( )
A.1个 B.2个 C.3个 D.4个
13.如图所示,,下列四个结论中,不正确的是( )
A. B.,且
C.和的面积相等 D.和的周长相等
14.如图,在四边形中,,点为上的点(不与重合),观察下列图形中全等三角形的对数. 其中,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…. 按此规律,第5个图中有( )对全等三角形.
A.15 B.16 C.18 D.21
15.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1C1B1是全等(合同)三角形,且点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图①所示);若运动方向相反,则称它们是镜面合同三角形(如图②所示),两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个进行翻折.
下列各组合同三角形中,是镜面合同三角形的是( )
A. B. C. D.
二、填空题
16.如图,,,点在边上,则的度数为 .
17.如图,已知,并将它们摆成如图所示的形式,那么的度数等于 .
18.如图, BFD≌ CED,若的面积为,的面积为2,则的面积为 .
19.如图,在 ABC中,厘米,厘米,且,点D为的中点.如果点P在线段上以v厘米/秒的速度由B点向C点运动,同时,点在线段上由C点向A点运动.若点的运动速度为4厘米/秒,则当与 CQP全等时,v的值为 .
三、解答题
20.把如图所示的由16个小正方形组成的图形,用三种不同的方法沿网格线分割成两个全等图形.
21.如图,,连接,与交于点,,,.(1)求的度数;(2)求的度数.
22.如图,,且点B,D,C在一条直线上,点F在上,延长交于点E.(1)试说明:.(2)若,,求的长.
23.如图,在 ABC中,点、分别在边、上,连接、交于点,且.(1)求证:是等腰直角三角形;(2)若,,求四边形的面积.
24.如图,A,E,C三点在同一直线上,且.
(1)求证:;(2)猜想:当 ADE满足什么条件时?并证明你的猜想.
参考答案
一、单选题
1.C
【详解】解:A、两个图形不能完全重合,不是全等图形,故本选项不符合题意;
B、两个图形不能完全重合,不是全等图形,故本选项不符合题意;
C、两个图形能完全重合,是全等图形,故本选项符合题意;
D、两个图形不能完全重合,不是全等图形,故本选项不符合题意;故选:C.
2.C
【详解】解:A、形状相等的两个图形不一定全等,可能图形的大小不同,本选项说法错误;
B、两个三角形不一定全等,三角形的形状和大小不能确定,本选项说法错误;
C、两个全等的图形面积是一定相等的,本选项说法正确;
D、两个正方形不一定全等,因为两个正方形的边长可能不等,本选项说法错误;故选:C.
3.B
4.C
【详解】解:①全等三角形的对应边相等,对应角相等,正确;
②全等三角形的周长相等,面积相等,正确;③面积相等的三角形形状不一定相同,故错误;
④周长相等的三角形形状不一定相同,故错误.所以①②正确,故选:C.
5.A
【详解】解:由图可知:是边长为的边的一个邻角,∵两个三角形全等,∴;故选A.
6.D
【详解】解:∵,∴因点M、P在方格正方形的两个对角顶点上,故点M、Q也应在方格正方形的两个对角顶点上.所以点Q是图中点D的位置,如下图:故选:D.
,
7.C
【详解】解:∵,∴,
∴,故选:C.
8.D
【详解】解∶∵,,∴,,
∵,∴,故选∶D.
9.D
【详解】解:,
,,,,故选项C正确,不符合题意;
,;故选项A正确,不符合题意;
,,
故选项D错误,符合题意;故选项B正确,不符合题意;故选:D.
10.C
【详解】解:图中两个三角形全等,,,.故选:C.
11.B
【详解】解:∵四边形为梯形,上底,下底,四边形是由8个全等梯形拼接而成,∴.故选:B.
12.C
【详解】延长交于H,延长交于F,
∵,∴
∴,
∴,∴故①②正确,
∴,故③是错误的,
∵,∴,故④是正确的,故选:C.
13.A
【详解】解:∵,∴,,
∴,,故选项A不正确,符合题意;
,和的周长相等,和的面积相等,故选项B、C、D正确,不符合题意;故选:A.
14.D
【详解】解:根据题意,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…第个图中,有对全等三角形,
∴第5个图中有对全等三角形.故选:D.
15.B
【详解】根据真正合同三角形的定义可知,选项A,C,D是真正合同三角形,选项B是镜面合同三角形,
故选:B.
二、填空题
16.
【详解】解:∵,,∴∴,
∴,故答案为:.
17.
【详解】解:∵∴,
∴
由题意可得,,
又∵∴故答案为;
18.7
【详解】解:∵ BFD≌ CED,∴,,
∴,∴,故答案为:.
19.3或4
【详解】解:中,厘米,点为的中点,厘米,
若,则需厘米,(厘米),
点的运动速度为4厘米秒,点的运动时间为:,(厘米秒);
若 BPD≌ CQP,则需厘米,,,解得:;
的值为3或4.故答案为:3或4.
三、解答题
20.解:分割线如图所示:
21.(1)解:∵,∴,
∴,∴,∵,∴.
(2)解:∵,,,∴,,
∵,∴,
∴,由(1)已得:,
∴.
22.(1)证明:∵,∴,,
∵点B,D,C在一条直线上,∴,
∵,∴,∴;
(2)解:∵,∴,,
∵,∴,∴.
23.(1)证明:,,,
,,是等腰直角三角形;
(2)解:,,,
,,四边形的面积.
24.(1)解:∵,∴,,∴;
(2)解:猜想,时,,∵,∴,
∵,∴,∴,
又,∴,∴当 ADE是直角三角形时,.
同课章节目录
