华东师大版八年级数学下册 课件:第19章 矩形、菱形与正方形 专题复习(共46张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册 课件:第19章 矩形、菱形与正方形 专题复习(共46张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-04 00:00:00 | ||
图片预览







文档简介
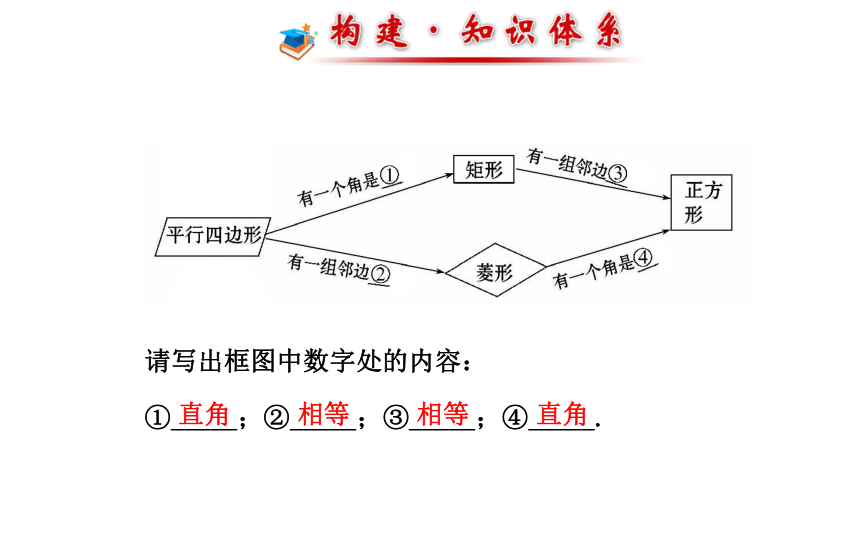
课件46张PPT。第19章 专题复习请写出框图中数字处的内容:
①_____;②_____;③_____;④_____.直角相等相等直角考点 1 矩形的性质与判定
【知识点睛】
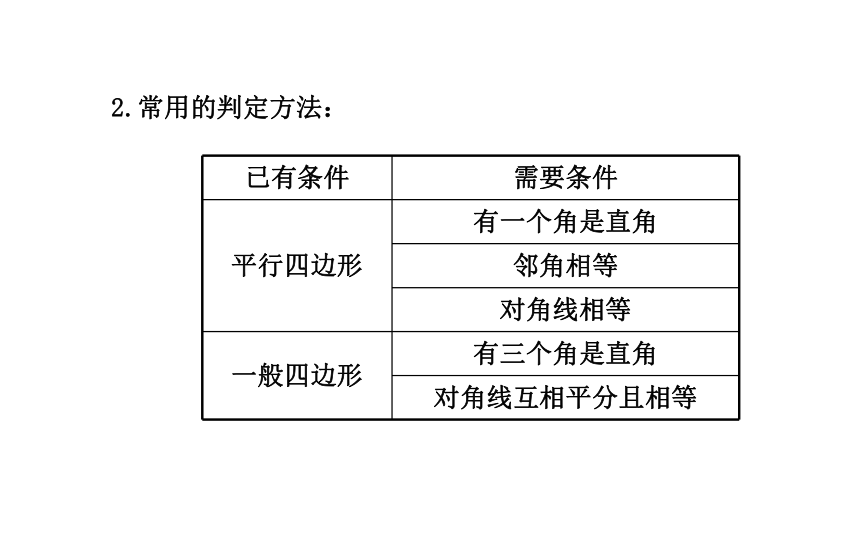
矩形的性质与判定方法
1.性质应用:
(1)证明线段的平行、相等或倍分关系.
(2)证明角相等或求角的度数.
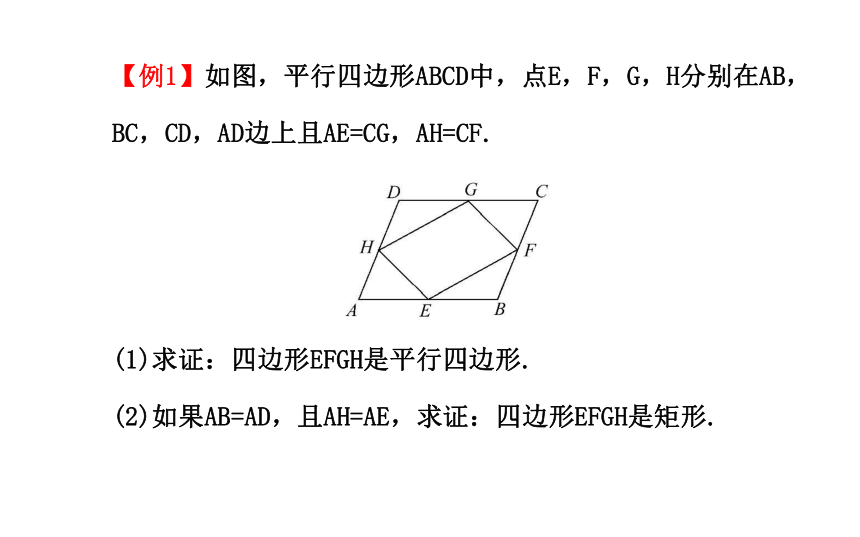
(3)解决与全等或相似有关的问题.2.常用的判定方法:【例1】如图,平行四边形ABCD中,点E,F,G,H分别在AB,BC,CD,AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形.
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.【思路点拨】(1)易证得△AEH≌△CGF,△BEF≌△DGH,从而证得EH=GF,GH=EF,根据两组对边分别相等的四边形是平行四边形得证.
(2)由题意,易证得∠EHG=90°,又由(1)知四边形EFGH是平行四边形,故四边形EFGH是矩形.【自主解答】(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB-AE=CD-CG,AD-AH=BC-CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH.∴GH=EF.
∴四边形EFGH是平行四边形.(2)在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°-α.
∵AE=AH,∴∠AHE=∠AEH=
∵AD=AB=CD,AH=AE=CG,
∴AD-AH=CD-CG,即DH=DG.
∴∠DHG=∠DGH=
∴∠EHG=180°-∠DHG-∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.【中考集训】
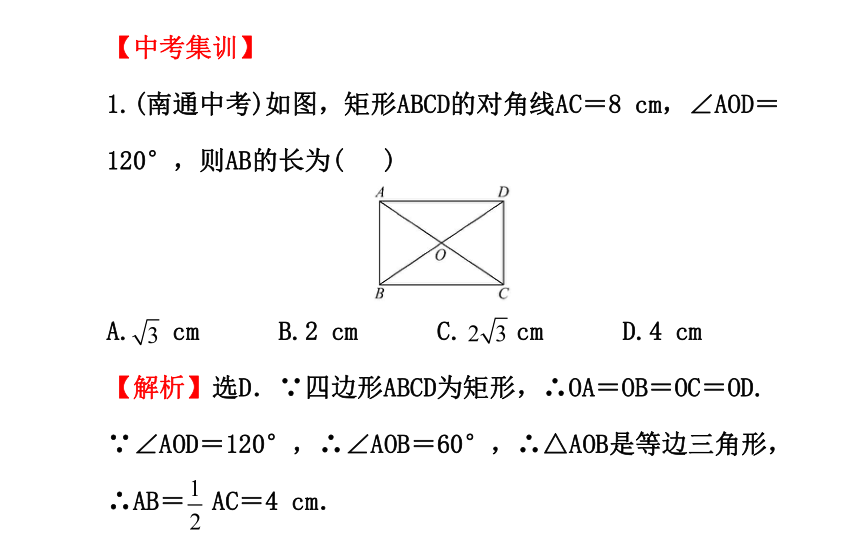
1.(南通中考)如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为( )
A. cm B.2 cm C. cm D.4 cm
【解析】选D.∵四边形ABCD为矩形,∴OA=OB=OC=OD. ∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB= AC=4 cm.2.(自贡中考)如图,矩形ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,连结BD,DF,则图中全等的直角三角形共有( )
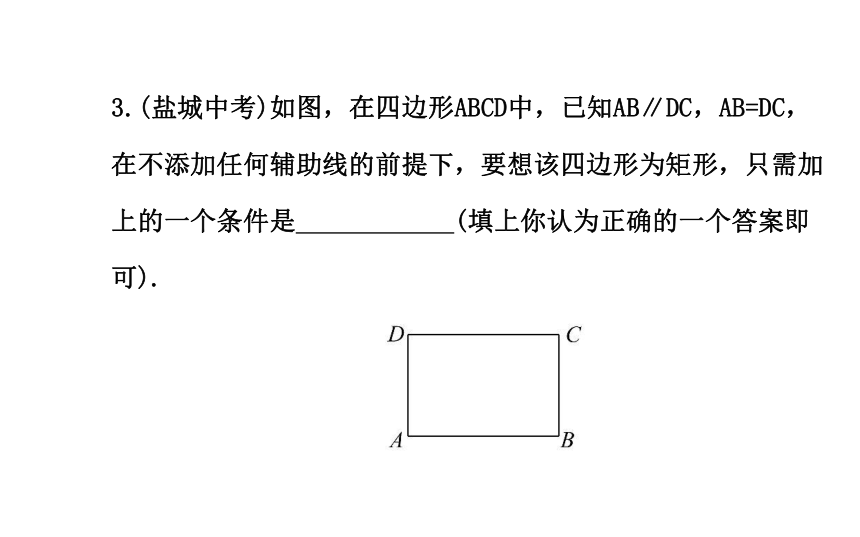
A.3对 B.4对 C.5对 D.6对【解析】选B.由矩形的性质可知,对角线分得的两个直角三角形全等,又因为E是CD中点,故DE=CE,且∠AED=∠FEC,∠ADE=∠FCE=90°,故△ADE≌△FCE,从而AD=CF,因此△BDC≌△FDC,进而△ADB≌△CFD,所以全等的直角三角形共有4对.3.(盐城中考)如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,只需加上的一个条件是 (填上你认为正确的一个答案即可).【解析】∵AB∥DC,AB=DC,∴四边形ABCD是平行四边形,而“有一个角是直角”的平行四边形是矩形,故可填的条件是:四边形ABCD内有一个直角.
答案:∠A=90°(答案不唯一)4.(肇庆中考)如图,四边形ABCD是矩形,对角线AC,
BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE.
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.【解析】(1)∵四边形ABCD是矩形,
∴AC=BD,AB∥CD.
又∵BE∥AC,∴四边形ABEC是平行四边形.
∴BE=AC,∴BD=BE.
(2)∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.
∵∠DBC=30°,∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC=
∴四边形ABED的面积= (4+8)×考点 2 菱形的性质与判定?
【知识点睛】
菱形的常用判定方法【例2】(娄底中考)如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点.
(1)求证:△MBA≌△NDC.
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.【思路点拨】(1)先由矩形性质确定∠A=∠C,AB=DC,再说明AM=NC,从而证明△MBA≌△NDC.
(2)先证明四边形MPNQ是平行四边形,再由PN=MP,可得四边形MPNQ是菱形.【自主解答】(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=DC,AD=BC,
∵M,N分别是AD,BC的中点,
∴AM=NC,
∴△MBA≌△NDC.
(2)四边形MPNQ是菱形.
理由:∵△MBA≌△NDC,
∴MB=DN,∠ABM=∠CDN,∵P,Q分别是BM,DN的中点.
∴PM=NQ,
∵∠ABM+∠CBM=90°,∠CDN+∠CND=90°,
∴∠CBM=∠CND,
∴PM∥NQ,
∴四边形MPNQ是平行四边形.
连结MN,由题意可得四边形AMNB是矩形,PN为直角三角形斜边上的中线,故PN=MP,
∴四边形MPNQ是菱形.【中考集训】
1.(成都中考)如图,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OC【解析】选B.菱形的对边平行且相等,所以AB∥DC;菱形的对角线一定垂直,所以AC⊥BD;菱形的对角线互相平分,所以OA=OC;菱形的对角线不一定相等.2.(厦门中考)如图,在菱形ABCD中,AC,BD是对角线,若∠BAC=50°,则∠ABC等于( )
A.40° B.50° C.80° D.100°【解析】选C.∵四边形ABCD是菱形,
∴∠BAC= ∠BAD,CB∥AD,
∵∠BAC=50°,
∴∠BAD=100°,
∵CB∥AD,
∴∠ABC+∠BAD=180°,
∴∠ABC=180°-100°=80°.3.(大连中考)如图,在菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24 C.28 D.40
【解析】选A.∵菱形对角线互相垂直平分,设O为AC,BD交点,∴BO=OD=3,AO=OC=4,
∴AB= =5,故菱形的周长为20.4.(温州中考)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD.
求证:四边形ACFD是菱形.【证明】方法一:∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
由平移变换的性质,得
CF=AD=10cm,DF=AC,
∴AD=CF=AC=DF,
∴四边形ACFD是菱形.方法二:由平移变换的性质,
得AD∥CF,AD=CF=10cm,
∴四边形ACFD是平行四边形.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
∴AD=AC,
∴□ACFD是菱形.【归纳整合】菱形的判定思路
(1)分析条件判定四边形是一个平行四边形.
(2)从边或对角线的关系判定平行四边形是一个菱形,这是一般的规律和方法.利用定义证明是最常用的办法.5.(济宁中考)如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC,AB于点E和F.
(1)在图中画出线段DE和DF.
(2)连结EF,则线段AD和EF互相垂直平分,这是为什么?【解析】(1)如图所示:(2)∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形.
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD.
∵AB∥DE,
∴∠FAD=∠EDA,
∴∠EAD=∠EDA,∴EA=ED,
∴平行四边形AEDF是菱形,
∴AD与EF互相垂直平分.考点 3 正方形的性质与判定?
【知识点睛】
判定正方形的一般思路【例3】(呼伦贝尔中考)如图,在△ABC中,点D是边BC的中点,DE⊥AC,DF⊥AB,垂足分别是E,F,且BF=CE.
(1)求证:DE=DF.
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.【思路点拨】(1)DE⊥AC,DF⊥AB→∠BFD=∠CED=90°→Rt△BDF≌Rt△CDE→DE=DF.
(2)∠A=90°→四边形AFDE是矩形 DF=DE 结论.【自主解答】(1)∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
在Rt△BDF和Rt△CDE中,
∵BD=CD,BF=CE,
∴Rt△BDF≌Rt△CDE,
∴DE=DF.(2)四边形AFDE是正方形.
证明:∵∠A=90°,DE⊥AC,DF⊥AB,
∴四边形AFDE是矩形,
又∵Rt△BDF≌Rt△CDE,∴DF=DE,
∴四边形AFDE是正方形.【中考集训】
1.(沈阳中考)如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个【解析】选C.∵四边形ABCD是正方形,
∴AB=BC=CD=AD,AO=OD=OC=OB,
∴△ABC,△BCD,△ADC,△ABD,△AOB,△BOC,△COD,△AOD都是等腰三角形,一共8个.2.(天津中考)如图,在边长为2的正方
形ABCD中,M为边AD的中点,延长MD至点E,
使ME=MC,以DE为边作正方形DEFG,点G在边
CD上,则DG的长为( )【解析】选D.∵四边形ABCD是正方形,
∴DC=DA=2,
∵M为边AD的中点,
∴DM=1,∴ME=MC=
∴DG=DE= -1.3.(青岛中考)已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明).【解析】(1)在矩形ABCD中,AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM.
(2)四边形MENF是菱形.
证明:E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NF=ME,∴四边形MENF是平行四边形,
由(1)得BM=CM,∴ME=MF,
∴平行四边形MENF是菱形.即四边形MENF是菱形.
(3)2∶1.4.(鞍山中考)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF.
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?【解析】(1)∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF.
∴CE=CF.
(2)GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠BCD=∠ECF=90°,又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG.∴GE=GF.
∴GE=GF=DF+GD=BE+GD.
①_____;②_____;③_____;④_____.直角相等相等直角考点 1 矩形的性质与判定
【知识点睛】
矩形的性质与判定方法
1.性质应用:
(1)证明线段的平行、相等或倍分关系.
(2)证明角相等或求角的度数.
(3)解决与全等或相似有关的问题.2.常用的判定方法:【例1】如图,平行四边形ABCD中,点E,F,G,H分别在AB,BC,CD,AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形.
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.【思路点拨】(1)易证得△AEH≌△CGF,△BEF≌△DGH,从而证得EH=GF,GH=EF,根据两组对边分别相等的四边形是平行四边形得证.
(2)由题意,易证得∠EHG=90°,又由(1)知四边形EFGH是平行四边形,故四边形EFGH是矩形.【自主解答】(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB-AE=CD-CG,AD-AH=BC-CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH.∴GH=EF.
∴四边形EFGH是平行四边形.(2)在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°-α.
∵AE=AH,∴∠AHE=∠AEH=
∵AD=AB=CD,AH=AE=CG,
∴AD-AH=CD-CG,即DH=DG.
∴∠DHG=∠DGH=
∴∠EHG=180°-∠DHG-∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.【中考集训】
1.(南通中考)如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为( )
A. cm B.2 cm C. cm D.4 cm
【解析】选D.∵四边形ABCD为矩形,∴OA=OB=OC=OD. ∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB= AC=4 cm.2.(自贡中考)如图,矩形ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,连结BD,DF,则图中全等的直角三角形共有( )
A.3对 B.4对 C.5对 D.6对【解析】选B.由矩形的性质可知,对角线分得的两个直角三角形全等,又因为E是CD中点,故DE=CE,且∠AED=∠FEC,∠ADE=∠FCE=90°,故△ADE≌△FCE,从而AD=CF,因此△BDC≌△FDC,进而△ADB≌△CFD,所以全等的直角三角形共有4对.3.(盐城中考)如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,只需加上的一个条件是 (填上你认为正确的一个答案即可).【解析】∵AB∥DC,AB=DC,∴四边形ABCD是平行四边形,而“有一个角是直角”的平行四边形是矩形,故可填的条件是:四边形ABCD内有一个直角.
答案:∠A=90°(答案不唯一)4.(肇庆中考)如图,四边形ABCD是矩形,对角线AC,
BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE.
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.【解析】(1)∵四边形ABCD是矩形,
∴AC=BD,AB∥CD.
又∵BE∥AC,∴四边形ABEC是平行四边形.
∴BE=AC,∴BD=BE.
(2)∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.
∵∠DBC=30°,∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC=
∴四边形ABED的面积= (4+8)×考点 2 菱形的性质与判定?
【知识点睛】
菱形的常用判定方法【例2】(娄底中考)如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点.
(1)求证:△MBA≌△NDC.
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.【思路点拨】(1)先由矩形性质确定∠A=∠C,AB=DC,再说明AM=NC,从而证明△MBA≌△NDC.
(2)先证明四边形MPNQ是平行四边形,再由PN=MP,可得四边形MPNQ是菱形.【自主解答】(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=DC,AD=BC,
∵M,N分别是AD,BC的中点,
∴AM=NC,
∴△MBA≌△NDC.
(2)四边形MPNQ是菱形.
理由:∵△MBA≌△NDC,
∴MB=DN,∠ABM=∠CDN,∵P,Q分别是BM,DN的中点.
∴PM=NQ,
∵∠ABM+∠CBM=90°,∠CDN+∠CND=90°,
∴∠CBM=∠CND,
∴PM∥NQ,
∴四边形MPNQ是平行四边形.
连结MN,由题意可得四边形AMNB是矩形,PN为直角三角形斜边上的中线,故PN=MP,
∴四边形MPNQ是菱形.【中考集训】
1.(成都中考)如图,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OC【解析】选B.菱形的对边平行且相等,所以AB∥DC;菱形的对角线一定垂直,所以AC⊥BD;菱形的对角线互相平分,所以OA=OC;菱形的对角线不一定相等.2.(厦门中考)如图,在菱形ABCD中,AC,BD是对角线,若∠BAC=50°,则∠ABC等于( )
A.40° B.50° C.80° D.100°【解析】选C.∵四边形ABCD是菱形,
∴∠BAC= ∠BAD,CB∥AD,
∵∠BAC=50°,
∴∠BAD=100°,
∵CB∥AD,
∴∠ABC+∠BAD=180°,
∴∠ABC=180°-100°=80°.3.(大连中考)如图,在菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24 C.28 D.40
【解析】选A.∵菱形对角线互相垂直平分,设O为AC,BD交点,∴BO=OD=3,AO=OC=4,
∴AB= =5,故菱形的周长为20.4.(温州中考)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD.
求证:四边形ACFD是菱形.【证明】方法一:∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
由平移变换的性质,得
CF=AD=10cm,DF=AC,
∴AD=CF=AC=DF,
∴四边形ACFD是菱形.方法二:由平移变换的性质,
得AD∥CF,AD=CF=10cm,
∴四边形ACFD是平行四边形.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
∴AD=AC,
∴□ACFD是菱形.【归纳整合】菱形的判定思路
(1)分析条件判定四边形是一个平行四边形.
(2)从边或对角线的关系判定平行四边形是一个菱形,这是一般的规律和方法.利用定义证明是最常用的办法.5.(济宁中考)如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC,AB于点E和F.
(1)在图中画出线段DE和DF.
(2)连结EF,则线段AD和EF互相垂直平分,这是为什么?【解析】(1)如图所示:(2)∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形.
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD.
∵AB∥DE,
∴∠FAD=∠EDA,
∴∠EAD=∠EDA,∴EA=ED,
∴平行四边形AEDF是菱形,
∴AD与EF互相垂直平分.考点 3 正方形的性质与判定?
【知识点睛】
判定正方形的一般思路【例3】(呼伦贝尔中考)如图,在△ABC中,点D是边BC的中点,DE⊥AC,DF⊥AB,垂足分别是E,F,且BF=CE.
(1)求证:DE=DF.
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.【思路点拨】(1)DE⊥AC,DF⊥AB→∠BFD=∠CED=90°→Rt△BDF≌Rt△CDE→DE=DF.
(2)∠A=90°→四边形AFDE是矩形 DF=DE 结论.【自主解答】(1)∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
在Rt△BDF和Rt△CDE中,
∵BD=CD,BF=CE,
∴Rt△BDF≌Rt△CDE,
∴DE=DF.(2)四边形AFDE是正方形.
证明:∵∠A=90°,DE⊥AC,DF⊥AB,
∴四边形AFDE是矩形,
又∵Rt△BDF≌Rt△CDE,∴DF=DE,
∴四边形AFDE是正方形.【中考集训】
1.(沈阳中考)如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个【解析】选C.∵四边形ABCD是正方形,
∴AB=BC=CD=AD,AO=OD=OC=OB,
∴△ABC,△BCD,△ADC,△ABD,△AOB,△BOC,△COD,△AOD都是等腰三角形,一共8个.2.(天津中考)如图,在边长为2的正方
形ABCD中,M为边AD的中点,延长MD至点E,
使ME=MC,以DE为边作正方形DEFG,点G在边
CD上,则DG的长为( )【解析】选D.∵四边形ABCD是正方形,
∴DC=DA=2,
∵M为边AD的中点,
∴DM=1,∴ME=MC=
∴DG=DE= -1.3.(青岛中考)已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明).【解析】(1)在矩形ABCD中,AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM.
(2)四边形MENF是菱形.
证明:E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NF=ME,∴四边形MENF是平行四边形,
由(1)得BM=CM,∴ME=MF,
∴平行四边形MENF是菱形.即四边形MENF是菱形.
(3)2∶1.4.(鞍山中考)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF.
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?【解析】(1)∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF.
∴CE=CF.
(2)GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠BCD=∠ECF=90°,又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG.∴GE=GF.
∴GE=GF=DF+GD=BE+GD.
